Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Phonon interference in single-molecule junctions

Nature Materials volume 24, pages 1258–1264 (2025)Cite this article

Subjects

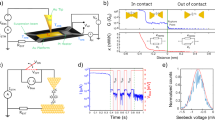
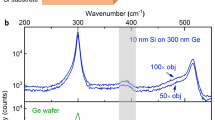
Abstract

Wave interference allows unprecedented coherent control of various physical properties and has been widely studied in electronic and photonic materials. However, the interference of phonons, or thermal vibrations, central to understanding coherent thermal transport in all electrically insulating materials, has been poorly characterized due to experimental challenges. Here we report the observation of phonon interference at room temperature in molecular-scale junctions. This is enabled by custom-developed scanning thermal probes with combined high stability and sensitivity, allowing quantification of heat flow through molecular junctions one molecule at a time. Using isomers of oligo(phenylene ethynylene)3 with either para- or meta-connected centre rings, our experiments revealed a remarkable reduction in thermal conductance in meta-conformations. Quantum-mechanically accurate molecular dynamics simulations show that this difference arises from the destructive interference of phonons through the molecular backbone. This work opens opportunities for studying numerous wave-driven material properties of phonons down to the single-molecule level that have remained experimentally inaccessible.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Twin-tip NbN SThM probe for single-molecule thermal measurement.
Fig. 2: Thermal and electrical measurements of single Au–BDA–Au molecular junctions.
Fig. 3: Observation of electrical and phonon interference effects in meta- and para-OPE3 single-molecule junctions.
Fig. 4: NEMD simulations of heat transport through OPE3-based single-molecule junctions.

Similar content being viewed by others

Data availability

The data supporting this study’s findings are available via figshare at https://doi.org/10.6084/m9.figshare.28462397 (ref. 61).

Code availability

The code used to analyse the data in this study is available from the corresponding author upon reasonable request.

References

  1. Chen, G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nat. Rev. Phys. 3, 555–569 (2021).

    Article  CAS  Google Scholar 

  2. Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 14, 667–674 (2015).

    Article  CAS  Google Scholar 

  3. Waldrop, M. M. The chips are down for Moore’s law. Nature 530, 144–147 (2016).

    Article  CAS  Google Scholar 

  4. Nomura, M. et al. Review of thermal transport in phononic crystals. Mater. Today Phys. 22, 100613 (2022).

    Article  CAS  Google Scholar 

  5. Tavakoli, A. et al. Heat conduction measurements in ballistic 1D phonon waveguides indicate breakdown of the thermal conductance quantization. Nat. Commun. 9, 4287 (2018).

    Article  Google Scholar 

  6. Luckyanova, M. N. et al. Coherent phonon heat conduction in superlattices. Science 338, 936–939 (2012).

    Article  CAS  Google Scholar 

  7. Ravichandran, J. et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 13, 168–172 (2013).

    Article  Google Scholar 

  8. Sivan, A. K. et al. GaAs/GaP superlattice nanowires for tailoring phononic properties at the nanoscale: implications for thermal engineering. ACS Appl. Nano Mater. 6, 18602–18613 (2023).

    Article  Google Scholar 

  9. Zen, N. et al. Engineering thermal conductance using a two-dimensional phononic crystal. Nat. Commun. 5, 3435 (2014).

    Article  Google Scholar 

  10. Maire, J. et al. Heat conduction tuning by wave nature of phonons. Sci. Adv. 3, e1700027 (2017).

    Article  Google Scholar 

  11. Lee, J. et al. Investigation of phonon coherence and backscattering using silicon nanomeshes. Nat. Commun. 8, 1–8 (2017).

    Google Scholar 

  12. Alaie, S. et al. Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature. Nat. Commun. 6, 7228 (2015).

    Article  CAS  Google Scholar 

  13. Aradhya, S. V. & Venkataraman, L. Single-molecule junctions beyond electronic transport. Nat. Nanotechnol. 8, 399–410 (2013).

    Article  CAS  Google Scholar 

  14. Dubi, Y. & Di Ventra, M. Colloquium: heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 83, 131–155 (2011).

    Article  CAS  Google Scholar 

  15. Cui, L., Miao, R., Jiang, C., Meyhofer, E. & Reddy, P. Perspective: thermal and thermoelectric transport in molecular junctions. J. Chem. Phys. 146, 092201 (2017).

    Article  Google Scholar 

  16. Gotsmann, B., Gemma, A. & Segal, D. Quantum phonon transport through channels and molecules—a perspective. App. Phys. Lett. 120, 160503 (2022).

    Article  CAS  Google Scholar 

  17. Markussen, T. Phonon interference effects in molecular junctions. J. Chem. Phys. 139, 244101 (2013).

    Article  Google Scholar 

  18. Klöckner, J. C., Cuevas, J. C. & Pauly, F. Tuning the thermal conductance of molecular junctions with interference effects. Phys. Rev. B 96, 245419 (2017).

    Article  Google Scholar 

  19. Chen, R., Sharony, I. & Nitzan, A. Local atomic heat currents and classical interference in single-molecule heat conduction. J. Phys. Chem. Lett. 11, 4261–4268 (2020).

    Article  CAS  Google Scholar 

  20. Sadeghi, H. Quantum and phonon interference-enhanced molecular-scale thermoelectricity. J. Phys. Chem. C 123, 12556–12562 (2019).

    Article  CAS  Google Scholar 

  21. Henry, A. & Chen, G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations. Phys. Rev. Lett. 101, 235502 (2008).

    Article  Google Scholar 

  22. Ren, J., Hänggi, P. & Li, B. Berry-phase-induced heat pumping and its impact on the fluctuation theorem. Phys. Rev. Lett. 104, 170601 (2010).

    Article  Google Scholar 

  23. Zhan, F., Li, N., Kohler, S. & Hänggi, P. Molecular wires acting as quantum heat ratchets. Phys. Rev. E 80, 061115 (2009).

    Article  Google Scholar 

  24. Menezes, M. G., Saraiva-Souza, A., Del Nero, J. & Capaz, R. B. Proposal for a single-molecule field-effect transistor for phonons. Phys. Rev. B 81, 012302 (2010).

    Article  Google Scholar 

  25. Díaz, E., Gutierrez, R. & Cuniberti, G. Heat transport and thermal rectification in molecular junctions: a minimal model approach. Phys. Rev. B 84, 144302 (2011).

    Article  Google Scholar 

  26. Segal, D. & Nitzan, A. Heat rectification in molecular junctions. J. Chem. Phys. 122, 194704 (2005).

    Article  Google Scholar 

  27. Bourgeois, O., André, E., Macovei, C. & Chaussy, J. Liquid nitrogen to room-temperature thermometry using niobium nitride thin films. Rev. Sci. Instrum. 77, 126108 (2006).

    Article  Google Scholar 

  28. Dechaumphai, E. & Chen, R. Sub-picowatt resolution calorimetry with niobium nitride thin-film thermometer. Rev. Sci. Instrum. 85, 094903 (2014).

    Article  Google Scholar 

  29. Cui, L. et al. Thermal conductance of single-molecule junctions. Nature 572, 628–633 (2019).

    Article  CAS  Google Scholar 

  30. Mosso, N. et al. Thermal transport through single-molecule junctions. Nano Lett. 19, 7614–7622 (2019).

    Article  CAS  Google Scholar 

  31. Guédon, C. M. et al. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 7, 305–309 (2012).

    Article  Google Scholar 

  32. Vazquez, H. et al. Probing the conductance superposition law in single-molecule circuits with parallel paths. Nat. Nanotechnol. 7, 663–667 (2012).

    Article  CAS  Google Scholar 

  33. Chen, Z. et al. Quantum interference enhances the performance of single-molecule transistors. Nat. Nanotechnol. 19, 1–7 (2024).

    Article  Google Scholar 

  34. Li, Y. et al. Gate controlling of quantum interference and direct observation of anti-resonances in single molecule charge transport. Nat. Mater. 18, 357–363 (2019).

    Article  CAS  Google Scholar 

  35. Frisenda, R., Janssen, V. A. E. C., Grozema, F. C., van der Zant, H. S. J. & Renaud, N. Mechanically controlled quantum interference in individual π-stacked dimers. Nat. Chem. 8, 1099–1104 (2016).

    Article  CAS  Google Scholar 

  36. Miao, R. et al. Influence of quantum interference on the thermoelectric properties of molecular junctions. Nano Lett. 18, 5666–5672 (2018).

    Article  CAS  Google Scholar 

  37. Bai, J. et al. Anti-resonance features of destructive quantum interference in single-molecule thiophene junctions achieved by electrochemical gating. Nat. Mater. 18, 364–369 (2019).

    Article  CAS  Google Scholar 

  38. Garner, M. H. et al. Comprehensive suppression of single-molecule conductance using destructive σ-interference. Nature 558, 416–419 (2018).

    Article  Google Scholar 

  39. Lee, W. et al. Heat dissipation in atomic-scale junctions. Nature 498, 209–212 (2013).

    Article  CAS  Google Scholar 

  40. Luo, T. & Chen, G. Nanoscale heat transfer—from computation to experiment. Phys. Chem. Chem. Phys. 15, 3389–3412 (2013).

    Article  CAS  Google Scholar 

  41. Cuevas, J. C. & Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment (World Scientific, 2017).

  42. Segal, D. & Agarwalla, B. K. Vibrational heat transport in molecular junctions. Ann. Rev. Phys. Chem. 67, 185–209 (2016).

    Article  CAS  Google Scholar 

  43. Cacelli, I. & Prampolini, G. Parametrization and validation of intramolecular force fields derived from DFT calculations. J. Chem. Theory Comput. 3, 1803–1817 (2007).

    Article  CAS  Google Scholar 

  44. Sääskilahti, K., Oksanen, J., Tulkki, J. & Volz, S. Role of anharmonic phonon scattering in the spectrally decomposed thermal conductance at planar interfaces. Phys. Rev. B 90, 134312 (2014).

    Article  Google Scholar 

  45. Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).

    Article  CAS  Google Scholar 

  46. Yelishala, S. C., Murphy, C. & Cui, L. Molecular perspective and engineering for thermal transport and thermoelectricity in polymers. J. Mat. Chem. A 12, 10614–10658 (2024).

    Article  CAS  Google Scholar 

  47. Cui, L. et al. Quantized thermal transport in single-atom junctions. Science 355, 1192–1195 (2017).

    Article  CAS  Google Scholar 

  48. Cui, L. et al. Study of radiative heat transfer in ångström- and nanometer-sized gaps. Nat. Commun. 8, 14479 (2017).

    Article  CAS  Google Scholar 

  49. Reid, M. T. H. & Johnson, S. G. Efficient computation of power, force, and torque in BEM scattering calculations. IEEE Trans. Antennas Propag. 63, 3588–3598 (2015).

    Article  Google Scholar 

  50. Gemma, A. et al. Full thermoelectric characterization of a single molecule. Nat. Commun. 14, 1–6 (2023).

    Article  Google Scholar 

  51. Thompson, A. P. et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).

    Article  CAS  Google Scholar 

  52. Tuckerman, M., Berne, B. J. & Martyna, G. J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 97, 1990–2001 (1992).

    Article  CAS  Google Scholar 

  53. Grønbech-Jensen, N. Complete set of stochastic Verlet-type thermostats for correct Langevin simulations. Mol. Phys. 118, 1662506 (2020).

    Article  Google Scholar 

  54. Schneider, T. & Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 17, 1302 (1978).

    Article  CAS  Google Scholar 

  55. Berendsen, H. J. C., Postma, J. P. M., Van Gunsteren, W. F., Dinola, A. & Haak, J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690 (1984).

    Article  CAS  Google Scholar 

  56. Sheng, H. W., Kramer, M. J., Cadien, A., Fujita, T. & Chen, M. W. Highly optimized embedded-atom-method potentials for fourteen FCC metals. Phys. Rev. B 83, 134118 (2011).

    Article  Google Scholar 

  57. Mahaffy, R., Bhatia, R. & Garrison, B. J. Diffusion of a butanethiolate molecule on a Au{111} surface. J. Phys. Chem. B 101, 771–773 (1997).

    Article  CAS  Google Scholar 

  58. Heinz, H., Lin, T. J., Kishore Mishra, R. & Emami, F. S. Thermodynamically consistent force fields for the assembly of inorganic, organic, and biological nanostructures: the INTERFACE force field. Langmuir 29, 1754–1765 (2013).

    Article  CAS  Google Scholar 

  59. Ventura‐Macias et al. Quantum mechanical derived (VdW‐DFT) transferable Lennard–Jones and Morse potentials to model cysteine and alkanethiol adsorption on Au (111). Adv. Mater. Inter. 11, 2400369 (2024).

    Article  Google Scholar 

  60. Fan, Z. et al. Force and heat current formulas for many-body potentials in molecular dynamics simulations with applications to thermal conductivity calculations. Phys. Rev. B 92, 094301 (2015).

    Article  Google Scholar 

  61. Yelishala, S. C. et al. Phonon interference in single-molecule junctions. figshare https://doi.org/10.6084/m9.figshare.28462397 (2025).

Download references

Acknowledgements

L.C. acknowledges support from the National Science Foundation (award number 2239004) and the College of Engineering and Applied Science at University of Colorado Boulder. We thank S. Bilan for technical support. P.M.M. acknowledges support from the Spanish Ministry of Education and Professional Formation (award number FPU21/06224). J.C.C. thanks the Spanish Ministry of Science and Innovation (award number PID2020-114880GB- I00) and the ‘Maria de Maeztu’ Programme for Units of Excellence in R&D (award number CEX2023-001316-M). J.G.V. acknowledges the Spanish CM ‘Talento Program’ (award number 2020-T1/ND-20306) and the Spanish Ministerio de Ciencia e Innovacion (award numbers PID2020-113722RJ-I00, TED2021-132219A-I00 and CNS2023-144011). This work utilized research computing resources at Picasso, Finisterrae3 (award numbers RES-FI-2023-0031 and RES-FI-2023-2-0006) and at the University of Colorado Boulder Research Computing, which is supported by the NSF (award numbers ACI-1532235 and ACI-1532236), the University of Colorado Boulder and Colorado State University.

Author information

Author notes

  1. These authors contributed equally: Sai C. Yelishala, Yunxuan Zhu, P. M. Martinez.

Authors and Affiliations

  1. Paul M. Rady Department of Mechanical Engineering, University of Colorado Boulder, Boulder, CO, USA

    Sai C. Yelishala, Yunxuan Zhu, Mohammad Habibi & Longji Cui

  2. Instituto de Ciencia de Materiales de Madrid (ICMM), CSIC, Madrid, Spain

    P. M. Martinez & J. G. Vilhena

  3. Departamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, Madrid, Spain

    P. M. Martinez & Juan Carlos Cuevas

  4. Department of Chemistry, University of Colorado Boulder, Boulder, CO, USA

    Hongxuan Chen & Wei Zhang

  5. CNR–Consiglio Nazionale delle Ricerche, Istituto di Chimica dei Composti Organo Metallici (ICCOM-CNR), Pisa, Italy

    Giacomo Prampolini

  6. Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, Madrid, Spain

    Juan Carlos Cuevas

  7. Materials Science and Engineering Program and Center for Experiments on Quantum Materials, University of Colorado Boulder, Boulder, CO, USA

    Longji Cui

Authors
  1. Sai C. Yelishala
    View author publications

    Search author on:PubMed Google Scholar

  2. Yunxuan Zhu
    View author publications

    Search author on:PubMed Google Scholar

  3. P. M. Martinez
    View author publications

    Search author on:PubMed Google Scholar

  4. Hongxuan Chen
    View author publications

    Search author on:PubMed Google Scholar

  5. Mohammad Habibi
    View author publications

    Search author on:PubMed Google Scholar

  6. Giacomo Prampolini
    View author publications

    Search author on:PubMed Google Scholar

  7. Juan Carlos Cuevas
    View author publications

    Search author on:PubMed Google Scholar

  8. Wei Zhang
    View author publications

    Search author on:PubMed Google Scholar

  9. J. G. Vilhena
    View author publications

    Search author on:PubMed Google Scholar

  10. Longji Cui
    View author publications

    Search author on:PubMed Google Scholar

Contributions

The project was conceived by L.C. The experiments were performed by S.C.Y. The twin-tip scanning thermal probes were fabricated by Y.Z. The MD simulations were performed by P.M.M., and the QM-FF was developed by G.P. The molecules were synthesized by H.C. under the supervision of W.Z. The near-field thermal simulations were performed by M.H. The manuscript was prepared by S.C.Y., P.M.M., J.C.C., J.G.V. and L.C., with comments and inputs from all authors.

Corresponding authors

Correspondence to Wei Zhang, J. G. Vilhena or Longji Cui.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Materials thanks Abraham Nitzan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Nanofabrication steps of the twin-tip SThM probe.

Step 1) NbN lines on two probe beams are defined and sputtered on the oxide surface. Steps 2 and 3) Cr/Au metallization layer and tunnelling current path are deposited via e-beam evaporation. Step 4) The shape of the probe beams is defined and formed using deep reactive ion etching. Step 5) The whole probe is released from the Si wafer. Step 6) Individual probes are aligned on a shadow mask. Step 7) The probe is fixed on the shadow mask. Step 8) A thin layer of gold film (100 nm) is deposited on the tip of the scanning probe. Step 9) The probe is detached from the shadow mask, cleaned, and installed into the UHV SPM chamber for measurements.

Extended Data Fig. 2 Thermal characterization of the SThM probe.

a, Temperature coefficient of resistance (TCR) and electrical resistance of NbN resistive thermometer as a function of temperature. b, The heating power required to increase the probe by a given temperature is plotted to obtain the thermal conductance of the probe. c, The normalized temperature increase on the probe as a function of heating frequency, where the thermal cut-off frequency (-3 dB point) is 14 Hz.

Extended Data Fig. 3 Thermal signal characterization.

a, Data recordings for different measurement schemes showing twin-tip scheme with peak-to-peak fluctuations of ± 3.5 µV, single-tip (that is, without matching probe) scheme with fluctuations of ± 15 µV, and no tip (that is, two precision resistors replacing the scanning thermal probes) scheme with equivalent fluctuations of ± 0.15 µV. b, Power Spectral Density (PSD) analysis for different schemes. The inset shows a logarithmic plot to elucidate the difference between each scheme. The shaded region indicates the reduced thermal drift when applying the twin-probe scheme as opposed to a single-tip scheme.

Extended Data Fig. 4 Measured electrical conductance histograms of three molecular junctions.

The black lines in (a-c) show the Gaussian peak of the histograms, providing the most probable conductance values of the junctions. These electrical conductance values are used to guide the thermal measurements to indicate the formation of a single-molecule junction.

Extended Data Fig. 5 Sample full approach-withdraw thermal and electrical conductance traces and evaluation of thermal background signal in the measurement of single-molecule junctions.

a, b, Two independent recordings of thermal and electrical traces during the approach, stop, and withdrawal of the scanning thermal probe on a para-OPE3 molecule sample. Before the formation of the single-molecule junction, the approach speed of the tip is at 200 pm s–1, and the withdraw speed is at 50 pm s–1. After the junction ruptures, a 10-nm piezo withdraw is applied at 3 nm s–1 (pink shaded region) to evaluate the background level of the thermal signal, which is observed to be ~100 pW K-1 and can be largely attributed to the near-field radiative heat transfer between the tip and the sample. c, Calculated near-field radiative heat transfer between a hot Au tip and Au substrate as a function of distance using SCUFF-EM. The shaded region is the error band and is ± one standard deviation from 25 different profiles of roughness. d, Thermal background signal of this study compared to previous single-molecule thermal measurements.

Extended Data Fig. 6 Geometry and interface potential independence of the lower thermal conductivity of meta-OPE3 compared to para-OPE3.

Cumulative integral of the thermal conductance \({{\rm{G}}}_{{\rm{th}}}^{{\rm{c}}}({\rm{\omega }})\) for various contact geometries for meta- (in pink) and para-OPE3 molecules (in red). Dashed lines show the total conductance values according to the energy exchange with the thermostats. The data corresponds to single production runs. The yellow shaded region represents the allowed frequencies inside the contacts, that is, the Debye frequency of gold ( ~ 161 cm–1). Each column corresponds to a different stable contact geometry. Left: pristine surfaces. Middle: molecule tethered in an Au terrace. Right: hollow-hollow contacts (fcc sites). Each row corresponds to a different Au-S interaction potential. Top row: Morse potential from ref. 57. Bottom row: Morse potential (PTH) from ref. 59. Histograms on the right margin correspond to the results shown in Fig. 3e to facilitate comparison with experiments.

Extended Data Fig. 7 Elastic thermal transport in single OPE3 junctions.

a, Spectral heat current q(ω) across meta-OPE3 evaluated at two different atomic planes within the same NEMD trajectory. Note that due to thermal noise, the signal fluctuates around 0 beyond 180 cm–1, although this has no impact on the total integral, as shown in the main text. The yellow shaded region represents the allowed frequencies inside the gold contacts, that is, gold Debye frequency ( ~ 161 cm–1). b, Contact geometry showing the different planes at which the spectral heat current shown in (a) are computed. The colour of each plane matches the plot. The position independence of the spectral heat current implies that the phonon transport in these junctions is essentially elastic. This justifies our theory analysis of the impact of phonon interferences in terms of the phonon transmission function and the corresponding transmission kernel.

Extended Data Fig. 8 Influence of thermal fluctuations on the transmission kernel (|dlr(ω)|2).

a, c, Distance between the last two layers of the Au tips during a NEMD trajectory for the meta-OPE3 (a) and para-OPE3 (c) junctions. Dashed lines highlight the selected distances for the calculation of the transmission kernel. b, d, Transmission kernel |dlr(ω)|2 for meta-OPE3 (b) and para-OPE3 (d) junctions locating both Au atoms at the distances shown in (a-c). Data shown in Fig. 4e was computed for gap sizes within one standard deviation for meta- and para-OPE3. In panel (b), arrows point at new destructive interference emerging at compressed conformations of the meta-OPE3 molecular contact. They appear in a frequency range (shaded region) void of normal modes both in the equilibrium state and in all configurations sampled from the dynamics. Note that such interferences are exclusively a dynamic effect, that is they would not appear in static-equilibrium calculations. Another remarkable feature of this dynamic destructive interference is that it results from a combination of several vibration modes building up systematically inside the aforementioned gap. This differs from the ‘two-mode’ destructive interference picture often used to describe this phenomenon.

Supplementary information

Supplementary Information

Supplementary Notes 1–10, Supplementary Figures 1–9 and Supplementary Tables 1–9.

Supplementary Video 1

All-atom NEMD trajectory sampled every 25 ps for 30 ns imposing a steady heat flux through the meta-OPE3 molecular junction from the hot reservoir (left at 330 K) towards the cold (right at 290 K). The hollow tip geometry prevents the molecule from diffusing and reduces the overall thermal conductance. Note how the thermal fluctuations experienced by the atoms in the junction, which are fully accounted for in the spectral heat flux q(ω) shown in Fig. 4c, largely deviate from small near-equilibrium oscillations assumed in static-DFT framework within the harmonic approximation.

Supplementary Video 2

All-atom NEMD trajectory sampled every 25 ps for 30 ns imposing a steady heat flux through the para-OPE3 molecular junction from the hot reservoir (left at 330 K) towards the cold (right at 290 K). The hollow tip geometry prevents the molecule from diffusing and reduces the overall thermal conductance. Note how the thermal fluctuations experienced by the atoms in the junction, which are fully accounted for in the spectral heat flux q(ω) shown in Fig. 4c, largely deviate from small near-equilibrium oscillations assumed in static-DFT framework within the harmonic approximation.

Supplementary Video 3

All-atom NEMD trajectory sampled every 25 ps for 30 ns imposing a steady heat flux through the meta-OPE3 molecular junction from the hot reservoir (left at 330 K) towards the cold (right at 290 K). The pristine gold surface allows for molecular diffusion across the gap between the reservoirs. Note how the thermal fluctuations experienced by the atoms in the junction, which are fully accounted for in the spectral heat flux q(ω) shown in Fig. 4c, largely deviate from small near-equilibrium oscillations assumed in static-DFT framework within the harmonic approximation.

Supplementary Video 4

All-atom NEMD trajectory sampled every 25 ps for 30 ns imposing a steady heat flux through the para-OPE3 molecular junction from the hot reservoir (left at 330 K) towards the cold (right at 290 K). The pristine gold surface allows for molecular diffusion across the gap between the reservoirs. Note how the thermal fluctuations experienced by the atoms in the junction, which are fully accounted for in the spectral heat flux q(ω) shown in Fig. 4c, largely deviate from small near-equilibrium oscillations assumed in static-DFT framework within the harmonic approximation.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yelishala, S.C., Zhu, Y., Martinez, P.M. et al. Phonon interference in single-molecule junctions. Nat. Mater. 24, 1258–1264 (2025). https://doi.org/10.1038/s41563-025-02195-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41563-025-02195-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing