Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Observation of non-Hermitian topology from optical loss modulation

Nature Materials volume 24, pages 1393–1399 (2025)Cite this article

Subjects

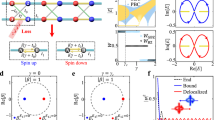
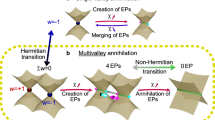
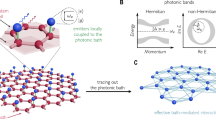
Abstract

Understanding the interplay of non-Hermiticity and topology is crucial given the intrinsic openness of most natural and engineered systems, and has important ramifications in topological lasers and sensors. Recently, it has been theoretically proposed that topological features could originate solely from a system’s non-Hermiticity in photonic platforms. Here we experimentally demonstrate the appearance of non-Hermitian topology exclusively from loss modulation in a photonic system that is topologically trivial in the absence of loss. We do this by implementing a non-Hermitian generalization of an Aubry–André–Harper model with purely imaginary potential in a programmable integrated photonics platform, which allows us to investigate different periodic and quasiperiodic configurations of the model. In both cases, we show the emergence of topological edge modes and explore their resilience to different kinds of disorder. Our work highlights loss engineering as a mechanism to generate topological properties.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Commensurate configurations with and without edge states.
Fig. 2: Theoretical and experimental characterization of the commensurate configurations with/without edge states.
Fig. 3: A quasiperiodic (incommensurate) configuration.
Fig. 4: Robustness against disorder in the loss and resonance frequency in the commensurate case.
Fig. 5: Robustness against disorder in the loss in the incommensurate case.

Similar content being viewed by others

Data availability

All experimental and simulation data supporting the findings are presented in the paper and the Supplementary Information in graphic form. Source data will be provided by the corresponding authors upon request.

References

  1. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).

    Article  CAS  Google Scholar 

  2. Price, H. et al. Roadmap on topological photonics. J. Phys. Photonics 4, 032501 (2022).

    Article  CAS  Google Scholar 

  3. Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).

    Article  PubMed  Google Scholar 

  4. Contractor, R. et al. Scalable single-mode surface-emitting laser via open-Dirac singularities. Nature 608, 692–698 (2022).

    Article  CAS  PubMed  Google Scholar 

  5. Kumar, A. et al. Topological sensor on a silicon chip. Appl. Phys. Lett. 121, 011101 (2022).

  6. Blanco-Redondo, A., Bell, B., Oren, D., Eggleton, B. J. & Segev, M. Topological protection of biphoton states. Science 362, 568–571 (2018).

    Article  CAS  PubMed  Google Scholar 

  7. Mittal, S., Goldschmidt, E. A. & Hafezi, M. A topological source of quantum light. Nature 561, 502–506 (2018).

    Article  CAS  PubMed  Google Scholar 

  8. Dai, T. et al. Topologically protected quantum entanglement emitters. Nat. Photonics 16, 248–257 (2022).

    Article  CAS  Google Scholar 

  9. Hashemi, A., Zakeri, M. J., Jung, P. S. & Blanco-Redondo, A. Topological quantum photonics. APL Photonics 10, 010903 (2025).

    Article  CAS  Google Scholar 

  10. Nasari, H., Pyrialakos, G. G., Christodoulides, D. N. & Khajavikhan, M. Non-Hermitian topological photonics. Opt. Mater. Express 13, 870–885 (2023).

    Article  CAS  Google Scholar 

  11. Yan, Q. et al. Advances and applications on non-Hermitian topological photonics. Nanophotonics 12, 2247–2271 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Kawabata, K., Shiozaki, K., Ueda, M. & Sato, M. Symmetry and topology in non-Hermitian physics. Phys. Rev. X 9, 041015 (2019).

    CAS  Google Scholar 

  13. Meng, H., Ang, Y. S. and Lee, C. H. Exceptional points in non-Hermitian systems: applications and recent developments. Appl. Phys. Lett. 124, 060502 (2024).

  14. Ding, K., Fang, C. & Ma, G. Non-hermitian topology and exceptional-point geometries. Nat. Rev. Phys. 4, 745–760 (2022).

    Article  Google Scholar 

  15. Rudner, M. S. & Levitov, L. S. Topological transition in a non-Hermitian quantum walk. Phys. Rev. Lett. 102, 065703 (2009).

    Article  CAS  PubMed  Google Scholar 

  16. Esaki, K., Sato, M., Hasebe, K. & Kohmoto, M. Edge states and topological phases in non-Hermitian systems. Phys. Rev. B 84, 205128 (2011).

    Article  Google Scholar 

  17. Diehl, S., Rico, E., Baranov, M. A. & Zoller, P. Topology by dissipation in atomic quantum wires. Nat. Phys. 7, 971–977 (2011).

    Article  CAS  Google Scholar 

  18. Schomerus, H. Topologically protected midgap states in complex photonic lattices. Opt. Lett. 38, 1912–1914 (2013).

    Article  PubMed  Google Scholar 

  19. Leykam, D., Bliokh, K. Y., Huang, C., Chong, Yi. Dong & Nori, F. Edge modes, degeneracies, and topological numbers in non-Hermitian systems. Phys. Rev. Lett. 118, 040401 (2017).

    Article  PubMed  Google Scholar 

  20. Reséndiz-Vázquez, P., Tschernig, K., Perez-Leija, A., Busch, K. & León-Montiel, Roberto de J. Topological protection in non-HermitianHaldane honeycomb lattices. Phys. Rev. Res. 2, 013387 (2020).

    Article  Google Scholar 

  21. Zeuner, J. M. et al. Observation of a topological transition in the bulk of a non-Hermitian system. Phys. Rev. Lett. 115, 040402 (2015).

    Article  PubMed  Google Scholar 

  22. Weimann, S. et al. Topologically protected bound states in photonic parity–time-symmetric crystals. Nat. Mater. 16, 433–438 (2017).

    Article  CAS  PubMed  Google Scholar 

  23. Zhao, H. et al. Non-Hermitian topological light steering. Science 365, 1163–1166 (2019).

    Article  CAS  PubMed  Google Scholar 

  24. Liu, Y. G. N., Jung, P. S., Parto, M., Christodoulides, D. N. & Khajavikhan, M. Gain-induced topological response via tailored long-range interactions. Nat. Phys. 17, 704–709 (2021).

  25. Weidemann, S., Kremer, M., Longhi, S. & Szameit, A. Topological triple phase transition in non-Hermitian Floquet quasicrystals. Nature 601, 354–359 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  26. Dai, T. et al. Non-Hermitian topological phase transitions controlled by nonlinearity. Nat. Phys. 20, 101–108 (2024).

    Article  CAS  Google Scholar 

  27. Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 358, 636–640 (2017).

    Article  CAS  PubMed  Google Scholar 

  28. St-Jean, P. et al. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 11, 651–656 (2017).

    Article  CAS  Google Scholar 

  29. Zhao, H. et al. Topological hybrid silicon microlasers. Nat. Commun. 9, 981 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  30. Takata, K. & Notomi, M. Photonic topological insulating phase induced solely by gain and loss. Phys. Rev. Lett. 121, 213902 (2018).

    Article  CAS  PubMed  Google Scholar 

  31. Zhu, B., Lang, Li-Jun, Wang, Q., Wang, Qi. Jie & Chong, Y. D. Topological transitions with an imaginary Aubry–André–Harper potential. Phys. Rev. Res. 5, 023044 (2023).

    Article  CAS  Google Scholar 

  32. Pereira, E. L., Li, H., Blanco-Redondo, A. & Lado, J. L. Non-Hermitian topology and criticality in photonic arrays with engineered losses. Phys. Rev. Res. 6, 023004 (2024).

  33. Liu, S. et al. Gain- and loss-induced topological insulating phase in a non-Hermitian electrical circuit. Phys. Rev. Appl. 13, 014047 (2020).

    Article  CAS  Google Scholar 

  34. Gao, H. et al. Observation of topological edge states induced solely by non-Hermiticity in an acoustic crystal. Phys. Rev. B 101, 180303 (2020).

    Article  CAS  Google Scholar 

  35. Gao, H. et al. Non-Hermitian route to higher-order topology in an acoustic crystal. Nat. Commun. 12, 1888 (2021).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  36. Fan, H. et al. Hermitian and non-Hermitian topological edge states in one-dimensional perturbative elastic metamaterials. Mech. Syst. Signal Process. 169, 108774 (2022).

    Article  Google Scholar 

  37. Wetter, H., Fleischhauer, M., Linden, S. & Schmitt, J. Observation of a topological edge state stabilized by dissipation. Phys. Rev. Lett. 131, 083801 (2023).

    Article  CAS  PubMed  Google Scholar 

  38. On, M. B. et al. Programmable integrated photonics for topological Hamiltonians. Nat. Commun. 15, 629 (2024).

  39. Dai, T. et al. A programmable topological photonic chip. Nat. Mater. 23, 928–936 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  40. Capmany, J. & Pérez-López, D. Programming topological photonics. Nat. Mater. 23, 874–875 (2024).

  41. Cem, A., Sanchez-Jacome, D., Pérez-López, D. & Da Ros, F. Thermal crosstalk modeling and compensation for programmable photonic processors. In 2023 IEEE Photonics Conference, 1–2 (IEEE, 2023); https://doi.org/10.1109/IPC57732.2023.10360567

  42. Aubry, S. & Andre, G. Analyticity breaking and anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 3, 133 (1980).

    CAS  Google Scholar 

  43. Verbin, M., Zilberberg, O., Lahini, Y., Kraus, Y. E. & Silberberg, Y. Topological pumping over a photonic Fibonacci quasicrystal. Phys. Rev. B 91, 064201 (2015).

    Article  Google Scholar 

  44. Tambasco, Jean-Luc et al. Quantum interference of topological states of light. Sci. Adv. 4, eaat3187 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  45. Yuce, C. Pt symmetric Aubry–André model. Phys. Lett. A 378, 2024–2028 (2014).

    Article  CAS  Google Scholar 

  46. Longhi, S. Metal-insulator phase transition in a non-Hermitian Aubry–André–Harper model. Phys. Rev. B 100, 125157 (2019).

    Article  CAS  Google Scholar 

  47. Zeng, Q.-B., Yang, Y.-B. & Xu, Y. Topological phases in non-Hermitian Aubry–André–Harper models. Phys. Rev. B 101, 020201 (2020).

  48. Pyrialakos, G. G. et al. Bimorphic Floquet topological insulators. Nat. Mater. 21, 634–639 (2022).

    Article  CAS  PubMed  Google Scholar 

Download references

Acknowledgements

A.B.-R. acknowledges support by the NSF award number 2328993. E.L.P. acknowledges support from the Nokia Industrial Doctoral School in Quantum Technology. J.L.L. acknowledges financial support from the Research Council of Finland project numbers 331342 and 358088, and the Jane and Aatos Erkko Foundation. E.L.P. and J.L.L. acknowledge the computational resources provided by the Aalto Science-IT project.

Author information

Authors and Affiliations

  1. CREOL, The College of Optics and Photonics, University of Central Florida, Orlando, FL, USA

    Amin Hashemi & Andrea Blanco-Redondo

  2. Department of Applied Physics, Aalto University, Espoo, Finland

    Elizabeth Louis Pereira & Jose L. Lado

  3. Nokia Bell Labs, Cambridge, UK

    Hongwei Li

Authors
  1. Amin Hashemi
    View author publications

    Search author on:PubMed Google Scholar

  2. Elizabeth Louis Pereira
    View author publications

    Search author on:PubMed Google Scholar

  3. Hongwei Li
    View author publications

    Search author on:PubMed Google Scholar

  4. Jose L. Lado
    View author publications

    Search author on:PubMed Google Scholar

  5. Andrea Blanco-Redondo
    View author publications

    Search author on:PubMed Google Scholar

Contributions

A.B.-R. and A.H. conceived the experiment and simulations, analysed the results and wrote the paper. A.H. performed the experiments and simulations. J.L.L. and E.L.P. developed the supporting theory. All authors contributed to technical discussions and edited the paper.

Corresponding author

Correspondence to Andrea Blanco-Redondo.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Materials thanks Jianwei Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–5 and Notes 1–8.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hashemi, A., Pereira, E.L., Li, H. et al. Observation of non-Hermitian topology from optical loss modulation. Nat. Mater. 24, 1393–1399 (2025). https://doi.org/10.1038/s41563-025-02278-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41563-025-02278-8

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing