Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Exciton dressing by extreme nonlinear magnons in a layered semiconductor

Nature Nanotechnology volume 20, pages 617–622 (2025)Cite this article

Subjects

Abstract

Collective excitations presenting nonlinear dynamics are fundamental phenomena with broad applications. A prime example is nonlinear optics, where diverse frequency-mixing processes are central to communication and attosecond science, and extreme (>sixth-order) harmonic generation provides broad wavelength conversion. Leveraging recent progress in van der Waals magnetic semiconductors, we demonstrate nonlinear optomagnonic coupling. In the layered antiferromagnetic semiconductor CrSBr, we observe exciton states dressed by up to 20 harmonics of magnons, resulting from their extreme nonlinearities. We also create tunable optical sidebands via sum- and difference-frequency generation between two optically bright magnon modes under symmetry-breaking magnetic fields. Moreover, we can tune the observed difference-frequency generation mode into resonance with one of the fundamental magnons, which results in parametric amplification of magnons. Our findings realize the modulation of the optical-frequency exciton with the extreme nonlinearity of magnons at microwave frequencies, which could find applications in magnonics and hybrid quantum systems, and provide a method for optomagnonic neuromorphic computing devices.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Coupling of excitons and nonlinear magnons in CrSBr.
Fig. 2: Nonlinear coupling of coherently hybridized acoustic and optical magnon modes.
Fig. 3: Tunable DFG and parametric magnon amplification in CrSBr.
Fig. 4: Magnon high-harmonic generation.

Similar content being viewed by others

Data availability

The datasets generated during and/or analysed during this study are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.

References

  1. Cramer, J. et al. Magnon detection using a ferroic collinear multilayer spin valve. Nat. Commun. 9, 1089 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  2. Chumak, A. V. et al. Advances in magnetics roadmap on spin-wave computing. IEEE Trans. Magn. 58, 0800172 (2022).

    Article  CAS  Google Scholar 

  3. Pirro, P., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Advances in coherent magnonics. Nat. Rev. Mater. 6, 1114–1135 (2021).

    Article  Google Scholar 

  4. Zheng, S. et al. Tutorial: nonlinear magnonics. J. Appl. Phys. 134, 151101 (2023).

    Article  CAS  Google Scholar 

  5. Flebus, B., Rezende, S. M., Grundler, D. & Barman, A. Recent advances in magnonics. J. Appl. Phys. 133, 160401 (2023).

    Article  CAS  Google Scholar 

  6. Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K. & Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 12, 070101 (2019).

    Article  CAS  Google Scholar 

  7. Bae, Y. J. et al. Exciton-coupled coherent magnons in a 2D semiconductor. Nature 609, 282–286 (2022).

    Article  CAS  PubMed  Google Scholar 

  8. Diederich, G. M. et al. Tunable interaction between excitons and hybridized magnons in a layered semiconductor. Nat. Nanotechnol. 18, 23–28 (2023).

    Article  CAS  PubMed  Google Scholar 

  9. Först, M. et al. Nonlinear phononics as an ultrafast route to lattice control. Nat. Phys. 7, 854–856 (2011).

    Article  Google Scholar 

  10. Chumak, A. V., Serga, A. A. & Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 5, 4700 (2014).

    Article  CAS  PubMed  Google Scholar 

  11. Rodrigues, D. R. et al. Nonlinear dynamics of topological ferromagnetic textures for frequency multiplication. Phys. Rev. Appl. 16, 014020 (2021).

    Article  CAS  Google Scholar 

  12. Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photon. 8, 119–123 (2014).

    Article  CAS  Google Scholar 

  13. Demidov, V. E. et al. Generation of the second harmonic by spin waves propagating in microscopic stripes. Phys. Rev. B 83, 054408 (2011).

    Article  Google Scholar 

  14. Hermsdoerfer, S. J. et al. A spin-wave frequency doubler by domain wall oscillation. Appl. Phys. Lett. 94, 223510 (2009).

    Article  Google Scholar 

  15. Zhang, Z. et al. Terahertz-field-driven magnon upconversion in an antiferromagnet. Nat. Phys. 20, 788–793 (2024).

    Article  CAS  Google Scholar 

  16. Zhang, Z. et al. Terahertz field-induced nonlinear coupling of two magnon modes in an antiferromagnet. Nat. Phys. 20, 801–806 (2024).

    Article  CAS  Google Scholar 

  17. Telford, E. J. et al. Coupling between magnetic order and charge transport in a two-dimensional magnetic semiconductor. Nat. Mater. 21, 754–760 (2022).

    Article  CAS  PubMed  Google Scholar 

  18. Telford, E. J. et al. Layered antiferromagnetism induces large negative magnetoresistance in the van der Waals semiconductor CrSBr. Adv. Mater. 34, 2205639 (2020).

    Article  Google Scholar 

  19. Wilson, N. P. et al. Interlayer electronic coupling on demand in a 2D magnetic semiconductor. Nat. Mater. 20, 1657–1662 (2021).

    Article  CAS  PubMed  Google Scholar 

  20. Sun, Y. et al. Dipolar spin wave packet transport in a van der Waals antiferromagnet. Nat. Phys. 20, 794–800 (2024).

    Article  CAS  Google Scholar 

  21. Dirnberger, F. et al. Magneto-optics in a van der Waals magnet tuned by self-hybridized polaritons. Nature 620, 533–537 (2023).

    Article  CAS  PubMed  Google Scholar 

  22. Huang, C. et al. Extreme terahertz magnon multiplication induced by resonant magnetic pulse pairs. Nat. Commun. 15, 3214 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  23. Kapteyn, H. C., Murnane, M. M. & Christov, I. P. Extreme nonlinear optics: coherent X rays from lasers. Phys. Today 58, 39–46 (2005).

    Article  CAS  Google Scholar 

  24. Lee, K. et al. Magnetic order and symmetry in the 2D semiconductor CrSBr. Nano Lett. 21, 3511–3517 (2021).

    Article  CAS  PubMed  Google Scholar 

  25. Cham, T. M. J. et al. Anisotropic gigahertz antiferromagnetic resonances of the easy-axis van der Waals antiferromagnet CrSBr. Nano Lett. 22, 6716–6723 (2022).

    Article  CAS  PubMed  Google Scholar 

  26. MacNeill, D. et al. Gigahertz frequency antiferromagnetic resonance and strong magnon–magnon coupling in the layered crystal CrCl3. Phys. Rev. Lett. 123, 047204 (2019).

    Article  CAS  PubMed  Google Scholar 

  27. Ferray, M. et al. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 21, L31 (1988).

    Article  CAS  Google Scholar 

  28. Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys 7, 138–141 (2011).

    Article  CAS  Google Scholar 

  29. Boyd, R. W. Nonlinear Optics (Academic, 2008).

  30. Kamimaki, A., Iihama, S., Suzuki, K. Z., Yoshinaga, N. & Mizukami, S. Parametric amplification of magnons in synthetic antiferromagnets. Phys. Rev. Appl. 13, 044036 (2020).

    Article  CAS  Google Scholar 

  31. Fu, H., Huang, K., Watanabe, K., Taniguchi, T. & Zhu, J. Gapless spin wave transport through a quantum canted antiferromagnet. Phys. Rev. X 11, 021012 (2021).

    CAS  Google Scholar 

  32. Koerner, C. et al. Frequency multiplication by collective nanoscale spin-wave dynamics. Science 375, 1165–1169 (2022).

    Article  CAS  PubMed  Google Scholar 

  33. Pawbake, A. et al. Raman scattering signatures of strong spin–phonon coupling in the bulk magnetic van der Waals material CrSBr. Phys. Rev. B 107, 075421 (2023).

    Article  CAS  Google Scholar 

  34. Fiebig, M., Pavlov, V. V. & Pisarev, R. V. Second-harmonic generation as a tool for studying electronic and magnetic structures of crystals: review. J. Opt. Soc. Am. B 22, 96–118 (2005).

    Article  CAS  Google Scholar 

  35. Bai, Y. et al. High-harmonic generation from topological surface states. Nat. Phys. 17, 311–315 (2021).

    Article  CAS  Google Scholar 

  36. Li, X. F., L’Huillier, A., Ferray, M., Lompré, L. A. & Mainfray, G. Multiple-harmonic generation in rare gases at high laser intensity. Phys. Rev. A 39, 5751–5761 (1989).

    Article  CAS  Google Scholar 

  37. Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).

    Article  CAS  PubMed  Google Scholar 

  38. Au, Y. et al. Resonant microwave-to-spin-wave transducer. Appl. Phys. Lett. 100, 182404 (2012).

    Article  Google Scholar 

  39. Roslyak, O. & Mukamel, S. Photon entanglement signatures in difference-frequency-generation. Opt. Express 17, 1093–1106 (2009).

    Article  CAS  PubMed  Google Scholar 

Download references

Acknowledgements

We thank L. Fu, M. Rudner and G. Refael for discussions. This work was mainly supported by the Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division (DE-SC0012509). Sample fabrication and optical measurements are partially supported by AFOSR FA9550-19-1-0390 and FA9550-21-1-0460. Synthesis of the CrSBr crystals is supported by the NSF MRSEC on Precision-Assembled Quantum Materials (DMR-2011738). Structural and magnetic characterization measurements were conducted as part of the Programmable Quantum Materials, an Energy Frontier Research Center, funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, under award DE-SC0019443. X.X. acknowledges support from the State of Washington-funded Clean Energy Institute and from the Boeing Distinguished Professorship in Physics.

Author information

Author notes

  1. Geoffrey M. Diederich

    Present address: Department of Physics, University of Maryland Baltimore County, Baltimore, MD, USA

Authors and Affiliations

  1. Department of Physics, University of Washington, Seattle, WA, USA

    Geoffrey M. Diederich, Mai Nguyen, John Cenker, Jordan Fonseca, Sinabu Pumulo, Di Xiao & Xiaodong Xu

  2. Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, USA

    Youn Jue Bae

  3. Department of Chemistry, Columbia University, New York, NY, USA

    Daniel G. Chica, Xavier Roy & Xiaoyang Zhu

  4. Department of Materials Science and Engineering, University of Washington, Seattle, WA, USA

    Di Xiao & Xiaodong Xu

  5. Department of Physics and Astronomy, University of Delaware, Newark, DE, USA

    Yafei Ren

Authors
  1. Geoffrey M. Diederich
    View author publications

    Search author on:PubMed Google Scholar

  2. Mai Nguyen
    View author publications

    Search author on:PubMed Google Scholar

  3. John Cenker
    View author publications

    Search author on:PubMed Google Scholar

  4. Jordan Fonseca
    View author publications

    Search author on:PubMed Google Scholar

  5. Sinabu Pumulo
    View author publications

    Search author on:PubMed Google Scholar

  6. Youn Jue Bae
    View author publications

    Search author on:PubMed Google Scholar

  7. Daniel G. Chica
    View author publications

    Search author on:PubMed Google Scholar

  8. Xavier Roy
    View author publications

    Search author on:PubMed Google Scholar

  9. Xiaoyang Zhu
    View author publications

    Search author on:PubMed Google Scholar

  10. Di Xiao
    View author publications

    Search author on:PubMed Google Scholar

  11. Yafei Ren
    View author publications

    Search author on:PubMed Google Scholar

  12. Xiaodong Xu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

X.X., D.X., Y.R. and G.M.D. conceived the project. G.M.D. performed the measurements with help from M.N., S.P., J.C. and J.F. M.N., S.P. and J.C. fabricated the samples. G.M.D., M.N., J.C., Y.J.B., X.Z., Y.R., D.X. and X.X. analysed the data and interpreted the results. Y.R. and D.X. built the model and performed the simulations. D.G.C. and X.R. grew the CrSBr crystals. G.M.D., M.N., X.Z., Y.R., D.X. and X.X. wrote the manuscript with input from all authors. All authors discussed the results.

Corresponding authors

Correspondence to Di Xiao, Yafei Ren or Xiaodong Xu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Nanotechnology thanks Zhanghai Chen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

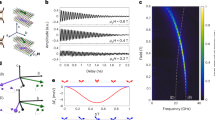
Extended Data Fig. 1 Field dependent transient reflectivity data.

a, Raw transient reflectivity data corresponding to the spectrum presented in Fig. 1d. b, Linecut taken from (a) at µoH ≈ 0.45 T. c, Same data as in (a) with the exponential decay removed. d, Linecut taken from (c) at µoH ≈ 0.45 T.

Extended Data Fig. 2 Magnon HHG under c axis field.

a, Transient reflectivity data from CrSBr under a field applied along the c (hard) crystal (magnetic) axis. b, Corresponding magnon spectrum presenting the first few harmonic orders.

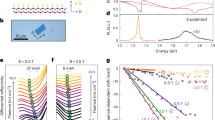
Extended Data Fig. 3 Field angle dependent transient reflectivity data.

a, Raw transient optical reflectivity data corresponding to the spectrum presented in Fig. 3a. b, Same data as in (a) with the exponential decay removed.

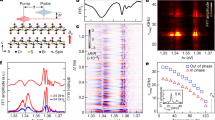
Extended Data Fig. 4 Comparison of field angle dependent data with simulations.

a, Same measured magnon spectrum presented in Fig. 3b. b, Simulated magnon spectrum. c, Additional dataset showing the DFG mode at positive and negative field angles.

Extended Data Fig. 5 HHG spectrum from an additional CrSBr sample.

a, Magnon spectrum presenting HHG from a ~ 90 nm thick flake, roughly half the thickness of the sample shown in the main text.

Extended Data Fig. 6 Model calculation of HHG.

The amplitude of the Fourier components as a function of frequency is shown. The amplitude first decays, then reaches a plateau, and then decays again. Both even and odd harmonics exist. The model parameters used to produce this spectrum are ω = 1 = 10ω0, v3 = 1, \({v}_{4}=\frac{1}{2}\), Γ = 10, and F(t) = 0.5sin (ω0t).

Source data

Source Data Fig. 1

Raw transient reflectivity data for Fig. 1.

Source Data Fig. 2

Raw transient reflectivity data and numerical data for Fig. 2.

Source Data Fig. 3

Raw transient reflectivity data for Fig. 3.

Source Data Fig. 4

Raw transient reflectivity data for Fig. 4.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Diederich, G.M., Nguyen, M., Cenker, J. et al. Exciton dressing by extreme nonlinear magnons in a layered semiconductor. Nat. Nanotechnol. 20, 617–622 (2025). https://doi.org/10.1038/s41565-025-01890-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41565-025-01890-8

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing