Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Quasi-phase-matched up- and down-conversion in periodically poled layered semiconductors

Nature Photonics volume 19, pages 291–299 (2025)Cite this article

Subjects

Abstract

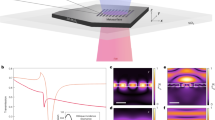
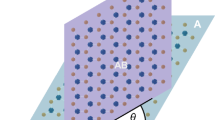
Nonlinear optics lies at the heart of classical and quantum light generation. The invention of periodic poling revolutionized nonlinear optics and its commercial applications by enabling robust quasi-phase-matching in crystals such as lithium niobate. However, reaching useful frequency conversion efficiencies requires macroscopic dimensions, limiting further technology development and integration. Here we realize a periodically poled van der Waals semiconductor (3R-MoS2). Owing to its large nonlinearity, we achieve a macroscopic frequency conversion efficiency of 0.03% at the relevant telecom wavelength over a microscopic thickness of 3.4 μm (that is, 3 poling periods), 10–100× thinner than current systems with similar performances. Due to intrinsic cavity effects, the thickness-dependent quasi-phase-matched second harmonic signal surpasses the usual quadratic enhancement by 50%. Further, we report the broadband generation of photon pairs at telecom wavelength via quasi-phase-matched spontaneous parametric down-conversion, showing a maximum coincidence-to-accidental ratio of 638 ± 75. This work opens the new and unexplored field of phase-matched nonlinear optics with microscopic van der Waals crystals, unlocking applications that require simple, ultra-compact technologies such as on-chip entangled photon-pair sources for integrated quantum circuitry and sensing.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: PPTMDs.
Fig. 2: Quasi-phase-matched SHG from PPTMDs.
Fig. 3: Theoretical simulations of QPM in PPTMDs.
Fig. 4: PPTMD second harmonic conversion efficiency.
Fig. 5: Quasi-phase-matched SPDC from PPTMDs.

Similar content being viewed by others

Data availability

All data generated or analysed during this study that support the plots within this paper and other findings of this study are available via Zenodo at https://doi.org/10.5281/zenodo.13987619 (ref. 59). Source data are provided with this paper.

References

  1. Boyd, R. W. Nonlinear Optics (Academic, 2020).

  2. Shih, Y. An Introduction to Quantum Optics: Photon and Biphoton Physics (Taylor & Francis, 2016).

  3. Fejer, M. M., Jundt, D. H., Byer, R. L. & Magelh, G. A. Quasi-phase-matched second harmonic generation: tuning and tolerances. IEEE J. Quantum Electron. 28, 2631–2654 (1992).

    ADS  Google Scholar 

  4. Myers, L. E. et al. Quasi-phase-matched optical parametric oscillators in bulk periodically poled LiNbO3. J. Opt. Soc. Am. B 12, 2102–2116 (1995).

    ADS  MATH  Google Scholar 

  5. Koh, S. et al. Sublattice reversal in GaAs/Si/GaAs (100) heterostructures by molecular beam epitaxy. Jpn. J. Appl. Phys. 37, L1493 (1998).

    MATH  Google Scholar 

  6. Eyres, L. A. et al. All-epitaxial fabrication of thick, orientation-patterned GaAs films for nonlinear optical frequency conversion. Appl. Phys. Lett. 79, 904–906 (2001).

    ADS  MATH  Google Scholar 

  7. Grisard, A. et al. Fabrication and applications of orientation-patterned gallium arsenide for mid-infrared generation. Phys. Status Solidi C 9, 1651–1654 (2012).

    ADS  MATH  Google Scholar 

  8. Gordon, L. et al. Diffusion-bonded stacked GaAs for quasiphase-matched second-harmonic generation of a carbon dioxide laser. Electron. Lett. 29, 1942–1944 (1993).

    ADS  MATH  Google Scholar 

  9. Tanimoto, R., Takahashi, Y. & Shoji, I. Quasi-phase-matching stack of 25 GaAs plates with high transmittance for high-power mid-infrared wavelength conversion fabricated by use of room-temperature bonding. Phys. Status Solidi C 38, (2021).

  10. Feng, D. et al. Enhancement of second-harmonic generation in LiNbO3 crystals with periodic laminar ferroelectric domains. Appl. Phys. Lett. 37, (1980).

  11. Feisst, A. & Koidl, P. Current induced periodic ferroelectric domain structures in LiNbO3 applied for efficient nonlinear optical frequency mixing. Appl. Phys. Lett. 47, (1985).

  12. Matsumoto, S., Lim, E. J., Hertz, H. M. & Fejer, M. M. Quasiphase-matched second harmonic generation of blue light in electrically periodically-poled lithium tantalate waveguides. Electron. Lett. 27, 2040–2042 (1991).

    ADS  Google Scholar 

  13. Van Der Poel, C. J., Bierlein, J. D., Brown, J. B. & Colak, S. Efficient type I blue second-harmonic generation in periodically segmented KTiOPO4 waveguides. Appl. Phys. Lett. 57, 20 (1990).

    Google Scholar 

  14. Hum, D. S. & Fejer, M. M. Quasi-phasematching. C. R. Phys. 8, 180–198 (2007).

    ADS  Google Scholar 

  15. Boes, A. et al. Lithium niobate photonics: unlocking the electromagnetic spectrum. Science 379, eabj4396 (2023).

    ADS  MATH  Google Scholar 

  16. Wang, C. et al. Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides. Optica 5, 1438–1441 (2018).

    ADS  MATH  Google Scholar 

  17. Suntsov, S., Rüter, C. E., Brüske, D. & Kip, D. Watt-level 775 nm SHG with 70% conversion efficiency and 97% pump depletion in annealed/reverse proton exchanged diced PPLN ridge waveguides. Opt. Express 29, 11386–11393 (2021).

    ADS  Google Scholar 

  18. Myers, L. E. & Bosenberg, W. R. Periodically poled lithium niobate and quasi-phase-matched optical parametric oscillators. IEEE J. Quantum Electron. 33, 10 (1997).

    MATH  Google Scholar 

  19. Yang, S. T. & Velsko, S. P. Frequency-agile kilohertz repetition-rate optical parametric oscillator based on periodically poled lithium niobate. Opt. Lett. 24, 133–135 (1999).

    ADS  Google Scholar 

  20. Lu, J. et al. Ultralow-threshold thin-film lithium niobate optical parametric oscillator. Optica 8, 539–544 (2021).

    ADS  Google Scholar 

  21. Ledezma, L. et al. Octave-spanning tunable infrared parametric oscillators in nanophotonics. Sci. Adv. 9, eadf9711 (2023).

    MATH  Google Scholar 

  22. Solntsev, A. S. et al. LiNbO3 waveguides for integrated SPDC spectroscopy. APL Photon. 3, 10 (2018).

    MATH  Google Scholar 

  23. Zhang, C. et al. Spontaneous parametric down-conversion sources for multiphoton experiments. Adv. Quantum Technol. 4, 2000132 (2021).

    Google Scholar 

  24. Krasnok, A., Tymchenko, M. & Alù, A. Nonlinear metasurfaces: a paradigm shift in nonlinear optics. Mater. Today 21, 8–21 (2018).

    Google Scholar 

  25. Wang, K., Chekhova, M. & Kivshar, Y. Metasurfaces for quantum technologies. Phys. Today 75, 3745–3763 (2022).

    MATH  Google Scholar 

  26. Fedotova, A. et al. Lithium niobate meta-optics. ACS Photon. 9, 3745–3763 (2022).

    Google Scholar 

  27. Santiago-Cruz, T. et al. Resonant metasurfaces for generating complex quantum states. Science 377, 991–995 (2022).

    ADS  MATH  Google Scholar 

  28. Neshev, D. N. & Miroshnichenko, A. E. Enabling smart vision with metasurfaces. Nat. Photon. 17, 26–35 (2023).

    ADS  MATH  Google Scholar 

  29. Zhu, S. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photon. 13, 242–352 (2021).

    MATH  Google Scholar 

  30. Jankowski, M. et al. Supercontinuum generation by saturated second-order nonlinear interactions. APL Photon. 8, 116104 (2023).

    ADS  MATH  Google Scholar 

  31. Guo, Q. et al. Ultrathin quantum light source with van der Waals NbOCl2 crystal. Nature 613, 53–59 (2023).

    ADS  MATH  Google Scholar 

  32. Wu, L. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350–355 (2017).

    MATH  Google Scholar 

  33. Mueller, T. & Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl. 2, 29 (2018).

    MATH  Google Scholar 

  34. Du, L. et al. Moiré photonics and optoelectronics. Science 379, eadg0014 (2023).

    MATH  Google Scholar 

  35. Ma, Q. et al. Photocurrent as a multiphysics diagnostic of quantum materials. Nat. Rev. Phys. 5, 170–184 (2023).

    MATH  Google Scholar 

  36. Sheffer, Y., Queiroz, R. & Stern, A. Symmetries as the guiding principle for flattening bands of Dirac fermions. Phys. Rev. X 13, 021012 (2023).

    Google Scholar 

  37. Malard, L. M. et al. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B. 87, 201401 (2013).

    ADS  MATH  Google Scholar 

  38. Li, Y. et al. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013).

    ADS  MATH  Google Scholar 

  39. Wang, G. et al. Giant enhancement of the optical second-harmonic emission of WSe2 monolayers by laser excitation at exciton resonances. Phys. Rev. Lett. 114, 097403 (2015).

    ADS  Google Scholar 

  40. Autere, A. et al. Nonlinear optics with 2D layered materials. Adv. Mater. 30, 1705963 (2018).

    Google Scholar 

  41. Wen, X. et al. Nonlinear optics of two-dimensional transition metal dichalcogenides. Wiley Online Library 1, 317–337 (2019).

    MATH  Google Scholar 

  42. Liu, W. et al. Recent advances of 2D materials in nonlinear photonics and fiber lasers. Adv. Optical Mater. 8, 1901631 (2020).

    Google Scholar 

  43. Dogadov, O. et al. Parametric nonlinear optics with layered materials and related heterostructures. Laser Photon. Rev. 16, 2100726 (2022).

    ADS  Google Scholar 

  44. Trovatello, C. et al. Optical parametric amplification by monolayer transition metal dichalcogenides. Nat. Photon. 15, 6–10 (2021).

    ADS  Google Scholar 

  45. Zhao, M. et al. Atomically phase-matched second-harmonic generation in a 2D crystal. Light Sci. Appl. 5, e16131 (2016).

    Google Scholar 

  46. Shi, J. et al. 3R MoS2 with broken inversion symmetry: a promising ultrathin nonlinear optical device. Adv. Mater. 29, 1701486 (2017).

    Google Scholar 

  47. Xu, X. et al. Towards compact phase-matched and waveguided nonlinear optics in atomically layered semiconductors. Nat. Photon. 16, 698–706 (2022).

    ADS  MATH  Google Scholar 

  48. Weissflog, M. A. et al. A tunable transition metal dichalcogenide entangled photon-pair source. Nat. Commun. 15, 7600 (2024).

    MATH  Google Scholar 

  49. Hong, H. et al. Twist-phase-matching in two-dimensional materials. Phys. Rev. Lett. 131, 233801 (2023).

    ADS  Google Scholar 

  50. Shoji, I., Kondo, T., Kitamoto, A., Shirane, M. & Ito, R. Absolute scale of second-order nonlinear-optical coefficients. J. Opt. Soc. Am. B 14, 2268–2294 (1997).

    ADS  Google Scholar 

  51. Wang, X.-L. et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 117, 210502 (2016).

    ADS  Google Scholar 

  52. Kuznetsov, A. I. et al. Roadmap for optical metasurfaces. ACS Photon. 11, 816–865 (2024).

    MATH  Google Scholar 

  53. Datta, I. et al. Low-loss composite photonic platform based on 2D semiconductor monolayers. Nat. Photon. 14, 256–262 (2020).

    ADS  MATH  Google Scholar 

  54. Paesani, S. et al. Generation and sampling of quantum states of light in a silicon chip. Nat. Phys. 15, 925–929 (2019).

    MATH  Google Scholar 

  55. Mannix, A. J. et al. Robotic four-dimensional pixel assembly of van der Waals solids. Nat. Nanotechnol. 17, 361–366 (2022).

    ADS  MATH  Google Scholar 

  56. Abdelwahab, I. et al. Giant second-harmonic generation in ferroelectric NbOI2. Nat. Photon. 16, 644–650 (2022).

    ADS  MATH  Google Scholar 

  57. Elshaari, A. W. et al. Hybrid integrated quantum photonic circuits. Nat. Photon. 14, 285–298 (2020).

    ADS  MATH  Google Scholar 

  58. Li, H. et al. Probing dynamical symmetry breaking using quantum-entangled photons. Quantum Sci. Technol. 3, 015003 (2017).

    ADS  MATH  Google Scholar 

  59. Trovatello, C. et al. Quasi-phase-matched up- and down-conversion in periodically poled layered semiconductors. Zenodo https://doi.org/10.5281/zenodo.13987619 (2024).

Download references

Acknowledgements

We thank B. Ursprung for the useful discussions. This work was supported by Programmable Quantum Materials, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences, under award DE-SC0019443. C.T. acknowledges the European Union’s Horizon Europe research and innovation programme under the Marie Skłodowska-Curie PIONEER HORIZON-MSCA-2021-PF-GF grant agreement no. 101066108. C.T. also acknowledges the Optica Foundation and Coherent Inc. for supporting this research through the Bernard J. Couillaud Prize 2022. G.C. acknowledges support by the Progetti di ricerca di Rilevante Interesse Nazionale (PRIN) of the Italian Ministry of Research 2022HL9PRP Overcoming the Classical limits of ultRafast spEctroSCopy with ENtangleD phOtons (CRESCENDO). C.T. and G.C. acknowledge funding from the European Union–NextGenerationEU under the National Quantum Science and Technology Institute (NQSTI) grant no. PE00000023-q-ANTHEM-CUP H43C22000870001. A.M. acknowledges funding from the European Union–NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant no. ECS00000041-VITALITY-CUP E13C22001060006, and Progetti di ricerca di Rilevante Interesse Nazionale (PRIN) of the Italian Ministry of Research PHOTO (Photonic Terahertz devices based on topological materials) no. 316 2020RPEPNH. A.Y. acknowledges support from the Department of Defense (DoD) through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program. J.P. acknowledges funding from the Air Force Office of Scientific Research (FA9550-21-1-0323) and the Office of Naval Research (N000142212841). P.W. acknowledges support from the Air Force Office of Scientific Research under award number FA8655-20-1-7030 (PhoQuGraph) and FA8655-23-1-7063 (TIQI). This research was funded in whole or in part by the Austrian Science Fund (FWF) (10.55776/F71). The financial support by the Austrian Federal Ministry of Labour and Economy, the National Foundation for Research, Technology and Development and the Christian Doppler Research Association is gratefully acknowledged. L.A.R. acknowledges support from the Erwin Schrödinger Center for Quantum Science and Technology (ESQ Discovery).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Columbia University, New York, NY, USA

    Chiara Trovatello, Zhi Hao Peng, Xinyi Xu & P. James Schuck

  2. Dipartimento di Fisica, Politecnico di Milano, Milano, Italy

    Chiara Trovatello & Giulio Cerullo

  3. CNR-SPIN, c/o Dipartimento di Scienze Fisiche e Chimiche, L’Aquila, Italy

    Carino Ferrante & Andrea Marini

  4. Department of Physics, Columbia University, New York, NY, USA

    Birui Yang, D. N. Basov & Cory R. Dean

  5. Faculty of Physics, Vienna Center for Quantum Science and Technology (VCQ), University of Vienna, Vienna, Austria

    Josip Bajo, Benjamin Braun, Philipp K. Jenke, Philip Walther & Lee A. Rozema

  6. Faculty of Physics and Vienna Doctoral School in Physics, University of Vienna, Vienna, Austria

    Josip Bajo, Benjamin Braun & Philipp K. Jenke

  7. Pritzker School of Molecular Engineering, University of Chicago, Chicago, IL, USA

    Andrew Ye & Jiwoong Park

  8. Department of Chemistry, Columbia University, New York, NY, USA

    Milan Delor

  9. James Franck Institute, University of Chicago, Chicago, IL, USA

    Jiwoong Park

  10. Department of Chemistry, University of Chicago, Chicago, IL, USA

    Jiwoong Park

  11. Christian Doppler Laboratory for Photonic Quantum Computer, University of Vienna, Vienna, Austria

    Philip Walther

  12. Department of Physical and Chemical Sciences, University of L’Aquila, L’Aquila, Italy

    Andrea Marini

  13. Istituto di Fotonica e Nanotecnologie, Consiglio Nazionale delle Ricerche, Milano, Italy

    Giulio Cerullo

Authors
  1. Chiara Trovatello
    View author publications

    Search author on:PubMed Google Scholar

  2. Carino Ferrante
    View author publications

    Search author on:PubMed Google Scholar

  3. Birui Yang
    View author publications

    Search author on:PubMed Google Scholar

  4. Josip Bajo
    View author publications

    Search author on:PubMed Google Scholar

  5. Benjamin Braun
    View author publications

    Search author on:PubMed Google Scholar

  6. Zhi Hao Peng
    View author publications

    Search author on:PubMed Google Scholar

  7. Xinyi Xu
    View author publications

    Search author on:PubMed Google Scholar

  8. Philipp K. Jenke
    View author publications

    Search author on:PubMed Google Scholar

  9. Andrew Ye
    View author publications

    Search author on:PubMed Google Scholar

  10. Milan Delor
    View author publications

    Search author on:PubMed Google Scholar

  11. D. N. Basov
    View author publications

    Search author on:PubMed Google Scholar

  12. Jiwoong Park
    View author publications

    Search author on:PubMed Google Scholar

  13. Philip Walther
    View author publications

    Search author on:PubMed Google Scholar

  14. Cory R. Dean
    View author publications

    Search author on:PubMed Google Scholar

  15. Lee A. Rozema
    View author publications

    Search author on:PubMed Google Scholar

  16. Andrea Marini
    View author publications

    Search author on:PubMed Google Scholar

  17. Giulio Cerullo
    View author publications

    Search author on:PubMed Google Scholar

  18. P. James Schuck
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.T., G.C., and P.J.S. conceived the experiment. C.T. also conceived of the design and realization of the samples and performed the measurements. C.F. and A.M. developed the theory model. J.B., B.B., C.T. and P.K.J. performed the spontaneous parametric down-conversion measurements. B.Y., C.T., Z.H.P., X.X. and A.Y. prepared the samples. X.X., C.T. and Z.H.P. built the experimental set-up and performed the morphological characterization of the samples. M.D., D.N.B., J.P., L.A.R., P.W., C.R.D., G.C. and P.J.S. supervised the study. C.T. wrote the paper with input from all authors.

Corresponding authors

Correspondence to Chiara Trovatello, Lee A. Rozema, Giulio Cerullo or P. James Schuck.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Maria Chekhova, Christiano de Matos, Qing Zhang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–12, discussion and Table 1.

Source data

Source Data Fig. 2

Experimental data of Fig. 2.

Source Data Fig. 3

Experimental data of Fig. 3.

Source Data Fig. 4

Experimental data of Fig. 4.

Source Data Fig. 5

Experimental data of Fig. 5.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Trovatello, C., Ferrante, C., Yang, B. et al. Quasi-phase-matched up- and down-conversion in periodically poled layered semiconductors. Nat. Photon. 19, 291–299 (2025). https://doi.org/10.1038/s41566-024-01602-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-024-01602-z

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing