Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Model-free estimation of the Cramér–Rao bound for deep learning microscopy in complex media

Nature Photonics volume 19, pages 593–600 (2025)Cite this article

Subjects

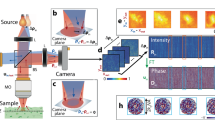
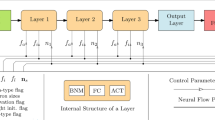
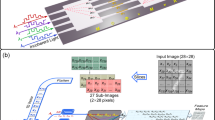
Abstract

Artificial neural networks have become important tools to harness the complexity of disordered or random photonic systems. Recent applications include the recovery of information from light that has been scrambled during propagation through a complex scattering medium, especially in the challenging case in which the deterministic input–output transmission matrix cannot be measured. This naturally raises the question of what the limit is that information theory imposes on this recovery process, and whether neural networks can actually reach this limit. To answer these questions, we introduce a model-free approach to calculate the Cramér–Rao bound, which sets the ultimate precision limit at which artificial neural networks can operate. As an example, we apply this approach in a proof-of-principle experiment using laser light propagating through a disordered medium, evidencing that a convolutional network approaches the ultimate precision limit in the challenging task of localizing a reflective target hidden behind a dynamically fluctuating scattering medium. The model-free method introduced here is generally applicable to benchmark the performance of any deep learning microscope, to drive algorithmic developments and to push the precision of metrology and imaging techniques to their ultimate limit.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Principle of the experiment.
Fig. 2: Demonstration of the Fisher information estimation procedure using numerically generated data.
Fig. 3: Comparison of different ANN architectures for the sample with optical thickness b = 4.2.
Fig. 4: Dependence of ANN precision on the optical thickness of the scattering sample.

Similar content being viewed by others

Data availability

The data generated in this study and scripts for data processing have been deposited in the University of Glasgow’s repository for research data with the following URL: https://doi.org/10.5525/gla.researchdata.1926.

References

  1. Moen, E. et al. Deep learning for cellular image analysis. Nat. Methods 16, 1233–1246 (2019).

    Article  Google Scholar 

  2. Tian, L. et al. Deep learning in biomedical optics. Lasers Surg. Med. 53, 748–775 (2021).

    Article  Google Scholar 

  3. Gebhart, V. et al. Learning quantum systems. Nat. Rev. Phys. 5, 141–156 (2023).

    Google Scholar 

  4. Tang, Y., Kurths, J., Lin, W., Ott, E. & Kocarev, L. Introduction to focus issue: when machine learning meets complex systems: networks, chaos, and nonlinear dynamics. Chaos 30, 063151 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  5. Barbastathis, G., Ozcan, A. & Situ, G. On the use of deep learning for computational imaging. Optica 6, 921–943 (2019).

    Article  ADS  Google Scholar 

  6. Zuo, C. et al. Deep learning in optical metrology: a review. Light Sci. Appl. 11, 39 (2022).

    Article  ADS  Google Scholar 

  7. Gigan, S. et al. Roadmap on wavefront shaping and deep imaging in complex media. J. Phys. Photon. 4, 042501 (2022).

    Article  Google Scholar 

  8. Yoon, S. et al. Deep optical imaging within complex scattering media. Nat. Rev. Phys. 2, 141–158 (2020).

    Article  Google Scholar 

  9. Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photon. 6, 283–292 (2012).

    Article  ADS  Google Scholar 

  10. Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).

    Article  ADS  Google Scholar 

  11. Conkey, D. B., Caravaca-Aguirre, A. M. & Piestun, R. High-speed scattering medium characterization with application to focusing light through turbid media. Opt. Express 20, 1733–1740 (2012).

    Article  ADS  Google Scholar 

  12. Yu, H. et al. Measuring large optical transmission matrices of disordered media. Phys. Rev. Lett. 111, 153902 (2013).

    Article  ADS  Google Scholar 

  13. Popoff, S. M., Lerosey, G., Fink, M., Boccara, A. C. & Gigan, S. Image transmission through an opaque material. Nat. Commun. 1, 81 (2010).

    Article  ADS  Google Scholar 

  14. Choi, Y. et al. Overcoming the diffraction limit using multiple light scattering in a highly disordered medium. Phys. Rev. Lett. 107, 023902 (2011).

    Article  ADS  Google Scholar 

  15. Horstmeyer, R., Ruan, H. & Yang, C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat. Photon. 9, 563–571 (2015).

    Article  ADS  Google Scholar 

  16. Denk, W., Strickler, J. H. & Webb, W. W. Two-photon laser scanning fluorescence microscopy. Science 248, 73–76 (1990).

    Article  ADS  Google Scholar 

  17. Horton, N. G. et al. In vivo three-photon microscopy of subcortical structures within an intact mouse brain. Nat. Photon. 7, 205–209 (2013).

    Article  ADS  Google Scholar 

  18. Huang, D. et al. Optical coherence tomography. Science 254, 1178–1181 (1991).

    Article  ADS  Google Scholar 

  19. Kashani, A. H. et al. Optical coherence tomography angiography: a comprehensive review of current methods and clinical applications. Progr. Retin. Eye Res. 60, 66–100 (2017).

    Article  Google Scholar 

  20. Bertolotti, J. et al. Non-invasive imaging through opaque scattering layers. Nature 491, 232–234 (2012).

    Article  ADS  Google Scholar 

  21. Katz, O., Heidmann, P., Fink, M. & Gigan, S. Noninvasive single-shot imaging through scattering layers and around corners via speckle correlations. Nat. Photon. 8, 784–790 (2014).

    Article  ADS  Google Scholar 

  22. Ando, T., Horisaki, R. & Tanida, J. Speckle-learning based object recognition through scattering media. Opt. Express 23, 33902–33910 (2015).

    Article  ADS  Google Scholar 

  23. Horisaki, R., Takagi, R. & Tanida, J. Learning-based imaging through scattering media. Opt. Express 24, 13738–13743 (2016).

    Article  ADS  Google Scholar 

  24. Li, S., Deng, M., Lee, J., Sinha, A. & Barbastathis, G. Imaging through glass diffusers using densely connected convolutional networks. Optica 5, 803–813 (2018).

    Article  ADS  Google Scholar 

  25. Li, Y., Xue, Y. & Tian, L. Deep speckle correlation: a deep learning approach toward scalable imaging through scattering media. Optica 5, 1181–1190 (2018).

    Article  ADS  Google Scholar 

  26. Sun, Y., Xia, Z. & Kamilov, U. S. Efficient and accurate inversion of multiple scattering with deep learning. Opt. Express 26, 14678–14688 (2018).

    Article  ADS  Google Scholar 

  27. Turpin, A., Vishniakou, I. & Seelig, J. D. Light scattering control in transmission and reflection with neural networks. Opt. Express 26, 30911–30929 (2018).

    Article  ADS  Google Scholar 

  28. Rahmani, B., Loterie, D., Konstantinou, G., Psaltis, D. & Moser, C. Multimode optical fiber transmission with a deep learning network. Light Sci. Appl. 7, 69 (2018).

    Article  ADS  Google Scholar 

  29. Lyu, M., Wang, H., Li, G., Zheng, S. & Situ, G. Learning-based lensless imaging through optically thick scattering media. Adv. Photon. 1, 036002 (2019).

    Article  ADS  Google Scholar 

  30. Caramazza, P., Moran, O., Murray-Smith, R. & Faccio, D. Transmission of natural scene images through a multimode fibre. Nat. Commun. 10, 2029 (2019).

    Article  ADS  Google Scholar 

  31. Zhu, C. et al. Image reconstruction through a multimode fiber with a simple neural network architecture. Sci. Rep. 11, 896 (2021).

    Article  Google Scholar 

  32. Resisi, S., Popoff, S. M. & Bromberg, Y. Image transmission through a dynamically perturbed multimode fiber by deep learning. Laser Photon. Rev. 15, 2000553 (2021).

    Article  ADS  Google Scholar 

  33. Li, Y., Cheng, S., Xue, Y. & Tian, L. Displacement-agnostic coherent imaging through scatter with an interpretable deep neural network. Opt. Express 29, 2244–2257 (2021).

    Article  ADS  Google Scholar 

  34. Starshynov, I., Turpin, A., Binner, P. & Faccio, D. Statistical dependencies beyond linear correlations in light scattered by disordered media. Phys. Rev. Res. 4, L022033 (2022).

    Article  Google Scholar 

  35. Rahmani, B. et al. Learning to image and compute with multimode optical fibers. Nanophotonics 11, 1071–1082 (2022).

    Article  Google Scholar 

  36. Bai, B. et al. All-optical image classification through unknown random diffusers using a single-pixel diffractive network. Light Sci. Appl. 12, 69 (2023).

    Article  ADS  Google Scholar 

  37. Abdulaziz, A., Mekhail, S. P., Altmann, Y., Padgett, M. J. & McLaughlin, S. Robust real-time imaging through flexible multimode fibers. Sci. Rep. 13, 11371 (2023).

    Article  ADS  Google Scholar 

  38. Huang, Z., Gu, Z., Shi, M., Gao, Y. & Liu, X. OP-FCNN: an optronic fully convolutional neural network for imaging through scattering media. Opt. Express 32, 444–456 (2024).

    Article  ADS  Google Scholar 

  39. Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222 (2011).

    Article  ADS  Google Scholar 

  40. Polino, E., Valeri, M., Spagnolo, N. & Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2, 024703 (2020).

    Article  ADS  Google Scholar 

  41. Cohen, S. D., Cavalcante, H. L., DdeS. & Gauthier, D. J. Subwavelength position sensing using nonlinear feedback and wave chaos. Phys. Rev. Lett. 107, 254103 (2011).

    Article  ADS  Google Scholar 

  42. del Hougne, P., Imani, M. F., Fink, M., Smith, D. R. & Lerosey, G. Precise localization of multiple noncooperative objects in a disordered cavity by wave front shaping. Phys. Rev. Lett. 121, 063901 (2018).

    Article  ADS  Google Scholar 

  43. del Hougne, P. Robust position sensing with wave fingerprints in dynamic complex propagation environments. Phys. Rev. Res. 2, 043224 (2020).

    Article  ADS  Google Scholar 

  44. Jauregui-Sánchez, Y., Penketh, H. & Bertolotti, J. Tracking moving objects through scattering media via speckle correlations. Nat. Commun. 13, 5779 (2022).

    Article  ADS  Google Scholar 

  45. Van Trees, H. L., Bell, K. L. & Tian, Z. Detection Estimation and Modulation Theory, Part I (John Wiley & Sons, 2013).

  46. Ober, R. J., Ram, S. & Ward, E. S. Localization accuracy in single-molecule microscopy. Biophys. J. 86, 1185 (2004).

    Article  ADS  Google Scholar 

  47. Deschout, H. et al. Precisely and accurately localizing single emitters in fluorescence microscopy. Nat. Methods 11, 253–266 (2014).

    Article  Google Scholar 

  48. Song, X., Xu, J., Liu, F., Han, T. X. & Eldar, Y. C. Intelligent reflecting surface enabled sensing: Cramér-Rao lower bound optimization. In 2022 IEEE Globecom Workshops (GC Wkshps) 413–418 (IEEE, 2022).

  49. Bouchet, D., Carminati, R. & Mosk, A. P. Influence of the local scattering environment on the localization precision of single particles. Phys. Rev. Lett. 124, 133903 (2020).

    Article  ADS  Google Scholar 

  50. Bouchet, D., Rotter, S. & Mosk, A. P. Maximum information states for coherent scattering measurements. Nat. Phys. 17, 564–568 (2021).

    Article  Google Scholar 

  51. Horodynski, M., Bouchet, D., Kühmayer, M. & Rotter, S. Invariance property of the Fisher information in scattering media. Phys. Rev. Lett. 127, 233201 (2021).

    Article  ADS  Google Scholar 

  52. Jolliffe, I. T. & Cadima, J. Principal component analysis: a review and recent developments. Phil. Trans. R. Soc. A 374, 20150202 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  53. Hyvärinen, A. & Oja, E. Independent component analysis: algorithms and applications. Neural Netw. 13, 411–430 (2000).

    Article  Google Scholar 

  54. Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016).

  55. Liu, R. et al. An intriguing failing of convolutional neural networks and the CoordConv solution. In Proc. 32nd International Conference on Neural Information Processing Systems NIPS’18 9628–9639 (Curran Associates, 2018).

  56. Huang, G., Liu, Z., Maaten, L. V. D. & Weinberger, K. Q. Densely connected convolutional networks. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2261–2269 (IEEE Computer Society, 2017).

  57. Barrett, H. H., Denny, J. L., Wagner, R. F. & Myers, K. J. Objective assessment of image quality. II. Fisher information, Fourier crosstalk, and figures of merit for task performance. J. Opt. Soc. Am. A 12, 834–852 (1995).

    Article  ADS  Google Scholar 

  58. Bouchet, D., Dong, J., Maestre, D. & Juffmann, T. Fundamental bounds on the precision of classical phase microscopes. Phys. Rev. Appl. 15, 024047 (2021).

    Article  ADS  Google Scholar 

  59. Szameit, A. et al. Sparsity-based single-shot subwavelength coherent diffractive imaging. Nat. Mater. 11, 455–459 (2012).

    Article  ADS  Google Scholar 

  60. Bouchet, D., Seifert, J. & Mosk, A. P. Optimizing illumination for precise multi-parameter estimations in coherent diffractive imaging. Opt. Lett. 46, 254–257 (2021).

    Article  ADS  Google Scholar 

  61. Feng, S., Kane, C., Lee, P. A. & Stone, A. D. Correlations and fluctuations of coherent wave transmission through disordered media. Phys. Rev. Lett. 61, 834 (1988).

    Article  ADS  Google Scholar 

  62. Akkermans, E. & Montambaux, G. Mesoscopic Physics of Electrons and Photons (Cambridge Univ. Press, 2007).

  63. Starshynov, I. et al. Non-Gaussian correlations between reflected and transmitted intensity patterns emerging from opaque disordered media. Phys. Rev. 8, 021041 (2018).

    Article  Google Scholar 

  64. Cao, H., Čižmár, T., Turtaev, S., Tyc, T. & Rotter, S. Controlling light propagation in multimode fibers for imaging, spectroscopy, and beyond. Adv. Opt. Photon. 15, 524–612 (2023).

    Article  Google Scholar 

  65. Stibůrek, M. et al. 110 µm thin endo-microscope for deep-brain in vivo observations of neuronal connectivity, activity and blood flow dynamics. Nat. Commun. 14, 1897 (2023).

    Article  Google Scholar 

  66. Sarafraz, H. et al. Speckle-enabled in vivo demixing of neural activity in the mouse brain. Biomed. Opt. Express 15, 3586–3608 (2024).

    Article  Google Scholar 

Download references

Acknowledgements

I.S. and D.F. acknowledge financial support from the UK Engineering and Physical Sciences Research Council (EPSRC grant nos. EP/T00097X/1 and EP/Y029097/1). D.F. acknowledges support from the UK Royal Academy of Engineering Chairs in Emerging Technologies Scheme. L.M.R. and S.R. were supported by the Austrian Science Fund (FWF) through project no. P32300 (WAVELAND).

Author information

Author notes

  1. These authors contributed equally: Ilya Starshynov, Maximilian Weimar.

Authors and Affiliations

  1. School of Physics and Astronomy, University of Glasgow, Glasgow, UK

    Ilya Starshynov & Daniele Faccio

  2. Institute for Theoretical Physics, Vienna University of Technology (TU Wien), Vienna, Austria

    Maximilian Weimar, Lukas M. Rachbauer, Günther Hackl & Stefan Rotter

  3. Université Grenoble Alpes, CNRS, LIPhy, Grenoble, France

    Dorian Bouchet

Authors
  1. Ilya Starshynov
    View author publications

    Search author on:PubMed Google Scholar

  2. Maximilian Weimar
    View author publications

    Search author on:PubMed Google Scholar

  3. Lukas M. Rachbauer
    View author publications

    Search author on:PubMed Google Scholar

  4. Günther Hackl
    View author publications

    Search author on:PubMed Google Scholar

  5. Daniele Faccio
    View author publications

    Search author on:PubMed Google Scholar

  6. Stefan Rotter
    View author publications

    Search author on:PubMed Google Scholar

  7. Dorian Bouchet
    View author publications

    Search author on:PubMed Google Scholar

Contributions

D.B. and I.S. conceived the idea and initiated the project. I.S. performed the experiments and data analysis under the supervision of D.F. and D.B. M.W. developed the numerical approach to calculate the Cramér–Rao bound and helped with the data analysis under the supervision of L.M.R., S.R. and D.B. G.H. helped in developing numerical methods and with the data analysis. I.S., M.W. and D.B. wrote the manuscript, with input from all authors.

Corresponding author

Correspondence to Dorian Bouchet.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Christophe Moser and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Sections 1–5 and Figs. 1–12.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Starshynov, I., Weimar, M., Rachbauer, L.M. et al. Model-free estimation of the Cramér–Rao bound for deep learning microscopy in complex media. Nat. Photon. 19, 593–600 (2025). https://doi.org/10.1038/s41566-025-01657-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-025-01657-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing