Main

Cell migration requires force generation by the actomyosin cytoskeleton, which can self-organize into specialized structures such as lamellipodial/filopodial protrusions and contractile cables1,2,3,4. Protrusions are driven by actin polymerization pushing against the membrane5, whereas retrograde flow generated by polymerizing actin at the leading edge of the cell and myosin contractility in the lamella are coupled to traction forces exerted through adhesion complexes onto the substrate1,6. During collective cell migration involved in multiple processes such as morphogenesis7, wound healing3,8 and tumour progression9, the migrating front exhibits variations in cell shape associated with large-scale changes of curvature10,11, resulting in either protrusions or contractile actomyosin cables8,10,12.

Although the mechanisms involved remain unclear, studies have pointed to the ability of cells to choose their migration mode by sensing the curvature of the extracellular environment, in both collectively migrating epithelial cells2,10 and single cells plated on micropatterns13,14,15. At the molecular scale, curvature sensors such as the BAR domain proteins and septins respond to membrane curvature at the nanometre-to-micrometre scales16,17. At the cell scale and beyond, however, curvature-sensing mechanisms are not well understood, although studies have suggested that cells can sense their own shapes18 and local curvature at this scale through actomyosin19. In particular, concave edges of the cell are associated with low substrate adhesiveness and the formation of actin cables15,20,21,22. Although the regulation of the cytoskeleton has been well studied in lamellipodium-based mechanisms23,24,25, its turnover and dynamic flow during actomyosin cable formation remain unclear.

Here, we report that the dynamic reorganization of actin filaments can act as a sensor of the sign of large-scale curvature. Concave edges promote the formation of polarized actin structures in which actomyosin flow is directed towards the cell edge, in contrast to observations made at convex leading-edge protrusions25,26. The switching of the organization and dynamics of actin cytoskeleton in response to either positive or negative curvature suggests that similar functional cytoskeletal components can give rise to different migration mechanisms, which help cells sense and navigate their environment and adapt to external physical cues.

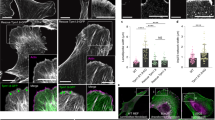
We first observed the actin organization at the leading edge of epithelial cells (Madin–Darby canine kidney cells, MDCK) with model wound closure assays27,28. The migrating front showed either convex (positive curvature, Fig. 1a, open arrowhead) or concave edges (negative curvature, Fig. 1a, filled arrowhead) showing lamellipodium-based crawling or actin cable assembly, respectively2,10. This actin cable at high negative curvature is connected to a continuous actomyosin structure, which extends into the cell and is connected to the substrate at the rear by focal adhesions (FAs) (Fig. 1b and Supplementary Fig. 1a,b).

Fig. 1: Negative curvature induces polarized actin structure formation during cell migration.
figure 1

a, Differential interference contrast microscopy (DIC) image showing the rough edge of an advancing MDCK monolayer emerging from a flat edge 10 h after removal of a rectangular polydimethylsiloxane (PDMS) block where protruding fingers are seen (open arrowhead) and regions between where negative curvature is generated (filled arrowhead). Scale bar, 20 μm. b, Enlarged view of the square inset in a, showing actin structure forming at negative curvature connected to FAs at the rear. Scale bar, 5 μm. c, Immunostaining of F-actin (with phalloidin in green and myosin IIA in magenta) during a gap closure assay with MDCK cells on a continuous fibronectin substrate, 15 min after the removal of the flower-shaped PDMS pattern. Cells form lamellipodial protrusions in response to the positive curvature ( + ) and form actin cables at negative curvatures ( − ). Scale bar, 15 μm. d, Zoom-in view of cells forming a lamellipodial protrusion at positive curvature in c. Scale bar, 5 μm. e, High-resolution SIM imaging of cells at negative curvature in gap closure experiments showing the actomyosin structure (different sample from c and d). Scale bar, 5 μm. f, Live-SIM imaging of actin in a spontaneously formed negative or positive curvature region at the leading edge of a GFP-actin-expressing MDCK monolayer on a continuous fibronectin substrate. The magenta line shows the edge of the cell and the white arrow shows the direction of migration. Scale bars, 2 μm. g, Kymographs along the yellow dashed lines in f showing (top) anterograde flow of actin fibres at negative curvature (horizontal scale bar, 1 μm; vertical scale bar, 10 min) and (bottom) retrograde flow at positive curvature (horizontal scale bar, 1 μm; vertical scale bar, 5 min). The magenta dashed line shows the leading edge of the cell. h, Schematic showing the sign of the curvature at the cell leading edge determines the actin flow direction, resulting in a different migration mechanism (top: anterograde flow at negative curvature results in suspended actin cable formation; bottom: retrograde flow at positive curvature results in lamellipodial protrusion). i, Time-lapse total internal reflection fluorescence (TIRF) images showing an MDCK monolayer migrating over a non-adherent circle (yellow dashed line, 30 μm diameter) while switching from lamellipodial protrusions to actomyosin cable in response to negative curvature induced by the non-adherent pattern; GFP-MRLC (myosin regulatory light chain) stable cells were transfected with mApple-actin. Scale bar, 15 μm. j, Kymograph along the white dashed line in i, showing the transition from lamellipodial protrusion (filled arrowhead) to actomyosin cable (open arrowhead). Horizontal scale bar, 5 μm; vertical scale bar, 20 min.

Full size image

To test whether geometrical constraint suffices to produce such actomyosin organization observed at negative curvatures, we designed flower-shaped patterns for a model wound assay27 (Fig. 1c and Supplementary Fig. 1c; see Supplementary Fig. 2a for details on the pattern geometry). At regions of negative curvature, we observed similar organizations of actomyosin and FA structures (Fig. 1e and Supplementary Fig. 1e), whereas at regions of positive curvature the cells showed lamellipodial protrusions (Fig. 1d and Supplementary Fig. 1d). The structures at negative curvatures showed a polarized organization of strong leading-edge actomyosin cable, immediately followed by a region of network-like actin fibres and myosin II, and FAs at the rear connected to radially oriented actin fibres, reminiscent of a variation of lamellipodium and lamella actin organization26,29,30. With live cell structured illumination microscopy (SIM), we observed an anterograde flow of actin fibres towards the leading edge, in contrast to the retrograde flow usually observed in lamellipodia and lamella at positive curvature (Fig. 1f,g)25,26. We thus hypothesized that the actomysosin system could serve as a cell-scale curvature sensor, establishing an anterograde flow at negatively curved edges that accumulate actin fibres and contractile cables at the front (Fig. 1h), whereas lamellipodium formation is promoted by the retrograde flow of actin fibres at positively curved edges26,29.

Migration over heterogeneous substrates31 and the cooperative nature of lamellipodium crawling and actin cable contraction during gap closure2 suggest that negative curvature-induced actin structures could facilitate monolayer migration over non-adhesive regions. To test this, MDCK cells were plated on micropatterned substrates composed of fibronectin-coated surfaces dotted with non-adherent circles (see Methods)28. When the MDCK monolayer migrated over non-adhesive regions, actin structures were formed as negatively curved cell edges were forced by cell crawling on either side of the circle (76.5 min–178.5 min in Fig. 1i). These structures actively promoted forward cellular movements over the non-adherent region (Fig. 1i, Supplementary Fig. 1i and Supplementary Video 1). As the cell encountered the non-adherent circle and the edge of the cell front adopted negative curvature, the migration mode switched from lamellipodial (Fig. 1j, filled arrowhead) to actomyosin cable (Fig. 1j, open arrowhead). This was accompanied by a switch from a retrograde to an anterograde flow of myosin (Fig. 1j, yellow dashed lines). These processes were not confined to collective cell migration processes, but were also observed within single cells such as Hela and U2OS when responding to negative curvature induced by heterogeneous micropatterned substrates (Supplementary Fig. 1f–h). We also created interconnected electro-spun fibre networks to mimic three-dimensional (3D) fibrous in vivo environments32 and seeded REF52 (rat embryonic fibroblast) cells onto the network (Supplementary Fig. 1j). In addition to attaching to the fibres, cells were also able to extend into empty spaces at cross-sections where a suspended (non-adherent) actin structure similar to the ones induced by negative curvature was observed (Supplementary Fig. 1k).

Next, we confined cells on flower-shaped patterns to immobilize cells and control cell geometry (Fig. 2a and Supplementary Fig. 2a). Cells responded to the curvature imposed by the pattern by consistently forming lamellipodial protrusions at positive curvatures and suspended actin cables at negative curvatures (Fig. 2b and Supplementary Video 2). The side view shows a difference in the 3D structure between opposite curvatures: a suspended cell part over the non-adherent region, with actin accumulation at its tip and continuous actomyosin staining along the ventral surface, for negative curvatures; and a lamellipodial protrusion close to the pattern edge for positive curvatures (Fig. 2c).

Fig. 2: Micropatterned substrate reproduces cellular-curvature-sensing polarized actin structure.
figure 2

a, Phase contrast image (left) of an MDCK cell colony showing lamellipodia formation at positive curvatures and suspended cell parts over non-adherent areas at negative curvatures; the edge of the fibronectin pattern (right) is shown with a magenta dotted line. Scale bars, 10 μm. b, Immunostaining of MDCK cells on the patterned surface: phalloidin (left), myosin IIA (middle) and merge (right phalloidin in red, myosin IIA in green, nucleus in blue and fibronectin pattern in cyan). The filled arrowhead shows suspended cable formation at negative curvature and the open arrowhead shows lamellipodial protrusion at positive curvature. Scale bars, 10 μm. c, xz view of cells at either negative (top) or positive (bottom) curvature. Note the extension of the cell body over the non-adherent region at negative curvature due to the forward pulling of suspended actin cable. Horizontal scale bar, 2 μm; vertical scale bar, 2 μm. d, Left: illustration with phalloidin staining image showing the local radial and transverse direction for a given point within the actin structure; the green line shows the fitted circle to the edge of fibronectin pattern and the red star shows the centre of the fitted circle. The radial direction is taken as the direction of the vector pointing from the point towards the centre of the fitted circle. Right: local orientation of actin fibres colour-coded for the angle between the fibre and local radial direction. Scale bar, 2 μm. e, Order parameter, S, decreases from the rear to the front of the cell. Error bars indicate s.e.m. n = 5. The red line shows the fitted model. f, Live SIM image showing sarcomeric organization of mApple-myosin IIA (green) and GFP-α-actinin (magenta). Scale bar, 1 μm. g, Intensity profile of α-actinin and myosin IIA along the white dashed line in f. h, Myosin IIA concentration profile from the rear to the front. Error bars indicate s.e.m. n = 10. i, F-actin (phalloidin) concentration profile from the rear to the front. Error bars indicate s.e.m. n = 10.

Full size image

We then analysed the organization and dynamics of the actin cytoskeleton at sub-cellular levels within regions abutting these negatively curved edges. Using SIM, we confirmed our previous observation that a polarized actin organization with radially oriented actin fibres (RFs) at the rear, transversely oriented actin fibres (TFs) near the front, and a suspended actin cable at the leading edge emerge in concave regions (Fig. 2d, see also Fig. 3a and Fig. 5l). As the actin structure occupies only part of the cell, the front and rear here and henceforth refer only to the actin structure and not the whole cell. This actin organization was quantified by the nematic order parameter S = < cos(2θ) > (where θ denotes the angle between the normal to the cell edge and the local actin filament orientation), which ranged from positive values at the rear to negative values at the front (Fig. 2d,e and Supplementary Fig. 2b,c), suggesting anisotropic actin organization33. TFs exhibited sarcomeric patterns of α-actinin and myosin IIA (Fig. 2f,g and Supplementary Fig. 2d), whereas RFs were associated with α-actinin and connected to FAs at the rear (Supplementary Fig. 2e). This structure recalls the lamella, where transverse arcs glide on radially oriented fibres30,34, yet presents a reversed organization. Similarly, the RFs connected to the FAs at the rear remained non-contractile, as shown by the absence of myosin IIA in this region, but the front part showed concentration gradients of both actin and myosin IIA, suggesting increased contractility (Fig. 2h,i).

Fig. 3: Negative curvature induces anterograde flow of actin.
figure 3

a, Representative 3D live SIM image showing radial fibre (RF) and transverse fibre (TF) organization at negative curvature. Colour-coded for cell height (0 μm being the surface of the coverslip). The magenta dashed line marks the edge of the fibronectin pattern. Scale bar, 5 μm. b, Kymograph along the white dashed line in a, showing anterograde flow of TFs and merging of TFs with actin cable at the edge. Horizontal scale bar, 1 μm; vertical scale bar, 10 min. c, Radial flow velocity of myosin flow at different substrate curvatures on patterned surfaces. Error bars indicate s.e.m. n = 10, 6, 8, 9, 13, 13, 9, 9, 6, 6, 9, 6, 6, 8, 10 for curvature values −0.200, −0.100, −0.0667, −0.0500, −0.0333, −0.0200, −0.0100, 0, 0.0100, 0.0200, 0.0333, 0.0500, 0.0667, 0.100, 0.200, respectively. A curvature value of 0 corresponds to regions of flat edges. Individual data points are shown as black dots, with red dots showing outliers. The red line shows the model fit to the negative curvature data (see text and Supplementary Information for details). d–f, Photoconversion of mEos2-actin on RF shows anterograde flow. d, mEos2-actin before photoconversion (green), the edge of the fibronectin pattern is marked by the white dashed line. e, mEos2-actin after photoconversion of a segment (magenta) on RF with a 405 nm laser. f, Kymograph along a photoconverted RF within the yellow box shown in d; the white dashed lines mark the edge of the fibronectin pattern. For d and e, scale bars, 2 μm; for f, horizontal scale bar, 1 μm, vertical scale bar, 1 min. g, Velocity vector map from fluorescent speckle microscopy (FSM) measurement. The magenta dashed line in g and h marks the edge of the fibronectin pattern. Scale bar, 5 μm. h, Heat map showing the magnitude of the actin flow velocity component along the radial direction in a representative cell at negative curvature measured by FSM. Scale bar, 5 μm. i, Decreasing flow profile of the radial velocity at negative curvature measured by FSM (blue, n = 3) and TF tracking (green, n = 5). Error bars indicate s.e.m. The red line shows the fitted model (see Supplementary Information for details).

Full size image

At negative curvatures, anterograde flow of TFs was observed in the cell, which coalesced at the front with the leading edge actin cable (Fig. 3a,b, Supplementary Fig. 3a,b and Supplementary Video 3). This contrasts with the retrograde flow observed at positive curvature regions (Supplementary Fig. 3c). The flow velocity of the TFs appeared to depend on the magnitude of the curvature, which was varied by changing the size of the pattern (Supplementary Fig. 3d). To investigate the relationship between flow velocity and the magnitude of the curvature, we designed patterned surfaces with edges comprised of semicircular shapes with a set of positive and negative curvatures separated by regions of flat edges (Supplementary Fig. 3e,f). By imaging cells transfected with mEos3.2 myosin IIA (see Methods), we measured the myosin flow velocity at different curvatures. This quantity showed a bi-phasic behaviour with an optimum value at curvature radii 15 and −20 μm, which is of the order of the cell size (Fig. 3c). This non-monotonic dependence of flow velocity on curvature can be explained in the framework of the physical model based on active gels (Supplementary Information). The anterograde flow at negative curvature was not restricted to the TFs, but occurred throughout the entire actin structure. First, photoconversion of RFs in mEos2-actin transfected cells revealed that RFs were engaged in anterograde flow (Fig. 3d–f and Supplementary Video 4). Then, by combining fluorescent speckle microscopy (FSM)35 (Fig. 3g,h and Supplementary Video 5) and direct TF tracking, we measured the flow profile across the entire actin structure. The actin flow velocity decreased from the rear (0.38 ± 0.05 μm min−1 starting from the RF region) to the front (0.17 ± 0.04 μm min−1 starting from the TF region) of the structure leading to the contractile cable at the edge (Fig. 3i). In comparison, the actin flow at positive curvature, where lamellipodium formation is preferred, increased from the rear to the front (Supplementary Fig. 3g–i and Supplementary Video 6). Altogether, these results show that concave regions promoted reverse actin flow patterns with rear-to-front actomyosin gradients, suggesting that these polarized structures may result from cell-generated active forces24.

To investigate the role of mechanics in the establishment and maintenance of these actin structures, we laser ablated actin fibres at different locations. Ablation of TFs resulted in recoil (Fig. 4a,b and Supplementary Video 7), suggesting that they were under tension. Contractility is necessary for directed actomyosin flow, as blebbistatin (25 μM) treatment stopped the myosin flow in MDCK cells (transfected with mApple Myosin IIA), which can be rescued by washout of the drug (Fig. 4c and Supplementary Video 8). Point ablations within the myosin-rich transition region allowed us to assess the local tension, based on the recoil velocity of the actomyosin meshwork (Fig. 4d,e and Supplementary Fig. 4a–d). Tension in the radial direction decreased from the rear to the front, whereas it increased in the transverse direction, resulting in a tension anisotropy gradient (Fig. 4f,g and Supplementary Fig. 4e,f) correlating well with the variation of the actin order parameter (Fig. 2e). This anisotropy gradient has also been shown to couple to actin flow36,37,38. We then used traction force microscopy (TFM)39 to visualize forces exerted by cells on the substrate along the edges of the pattern (Fig. 4h). We observed large traction forces along the actin cables at the edge (Fig. 4i, filled arrowheads). In contrast, outward pointing forces were generated at highly negative curvatures (Fig. 4i, open arrowhead), resulting from the tension within the actin gel exerting pulling forces on FAs localized at the edge of the pattern. In comparison, inward pointing forces are usually observed for cells crawling or spreading with positively curved outer edges (Fig. 4h)6,40. Here, the distinctive geometry of the actin structure led to cell traction forces at FA sites that are directed outwards towards the cell edge, in agreement with force patterns observed during in vitro wound healing39.

Fig. 4: Contractility and tension anisotropy gradient are coupled to anterograde flow of actin at negative curvature.
figure 4

a, Laser ablation along the radial direction (green dashed line) in the centre of the actin structure (GFP-MRLC in white overlaid with the fibronectin pattern in magenta) at negative curvature reveals that the actin cables are under tension. Scale bars, 5 μm. b, Kymograph along the yellow dashed line in a shows recoil of actin cables after each ablation (six ablation time points are indicated by filled arrowheads). Horizontal scale bar, 3 μm, vertical scale bar, 1 min. c, Flow of TFs depends on myosin II contractility; anterograde flow of myosin stops after 25 μM blebbistatin treatment and recovers after washout. Top: images of MDCK cells transfected with mApple myosin IIA in each condition. Scale bars, 5 μm. Bottom: corresponding kymographs along the yellow dashed line in each image above. Horizontal scale bars, 1 μm; vertical scale bars, 5 min. Note that the same cell was imaged for the three conditions. d, Point laser ablation near the rear of the actin structure. Scale bar, 5 μm. The yellow circle shows recoil after 5 s. e, Point laser ablation at the front of the actin structure. Scale bar, 5 μm. The yellow circle shows recoil after 5 s. f,g, Tension anisotropy increases from the rear to the front. Relative distances within 0.2–0.4 are measured for the rear (n = 6), and 0.6–0.8 for the front (n = 9). Red line in f shows the fitted model (see Supplementary Information for detail). For g, a two-sided t-test was used, p = 0.0027. A normal distribution was tested and confirmed with Anderson–Darling test at a 0.01 confidence interval. h, Traction force microscopy (TFM) reveals a geometry-induced traction force pattern at negative curvature. Scale bar, 5 μm. i, Image showing an enlarged view at negative curvature, corresponding to the yellow dashed line box in h. Filled arrowheads show traction forces parallel to the edge of the cell and the open arrowhead shows forward-pointing traction forces at the rear of the actin structure. Scale bar, 5 μm. j, Simulation of tension within the transition region. Fitted traction forces of 450 pN applied at the front (red arrows) and fixed boundary condition applied at the rear (red curve). Brown arrows indicate the directions of the calculated principal stresses. The colour map indicates the magnitude of the first principal stress. See Supplementary Information for a detailed description of the simulation.

Full size image

To further test our hypothesis of a coupling between tension anisotropy at negative curvatures and actin flow, we developed a model that describes the actin cytoskeleton as a two-dimensional (2D) active nematic gel41 (see Supplementary Information for details). We summarize here a one-dimensional analysis along the rear/front x axis of the suspended region (along the radial direction in Fig. 2d); a 2D numerical analysis of the stress field in the actin structure was also performed (Fig. 4j). The rear (that is, edge of the adhesive pattern) is given by x = 0, and the front (that is, edge of the suspended cell) is x = l. Following active gel theory38,41, the action of myosin II motors leads to an active contractile stress parameterized by positive constants ζ and ζ′. We allow the isotropic part ζ, which can be understood as a negative pressure42, to depend on the bound density of myosin motors cm, whereas, for simplicity, the anisotropic part ζ′ is assumed constant. Since the actin structure is suspended and non-adherent, we neglect friction forces with both membrane and cytosol as compared to viscous forces, as justified in ref. 43 (see also Supplementary Information). Thus, calling σ the tension along x in the gel, force balance is given by ∂xσ = 0. As a result, we find σ = λ/R, where λ is the line tension of the front stress fibre and R the radius of curvature of the actin structure front. Next, σ can be related to contractile activity and to the viscous stress η∂xv, where v(x) is the actin flow field along x; furthermore, due to fast actin turnover, pressure forces are neglected38; see Supplementary Information. Thus, we find the following linear equation that determines the flow profile (see Supplementary Information):

$$\partial _xv = - \frac{{\zeta - \frac{\lambda }{R}}}{\eta }$$
(1)

In addition, our active gel model provides a prescription for determining the nematic order parameter S(x), as described in the Supplementary Information.

This model reproduces key experimental features. First, equation (1) shows that the actin flow is generated by myosin activity and, as long as isotropic contractility is dominant, one finds ∂xv<0. This, together with the boundary condition v(l) = 0—which assumes no boundary-specific sources of actin turnover—shows that contractility induces an anterograde flow in the actin structure, as observed experimentally. Quantitatively, flow measurements reveal that the flow profile is fitted well by a linear dependence on x (Fig. 3i), which suggests that contractile terms in equation (1) can be assumed constant. The maximal flow speed can then be estimated as lζ/η, which gives 0.4 μm min−1 with standard values of ζ ~ 103 Pa and η ~ 105 Pa s (refs. 44,45), in agreement with observations. Second, this estimate of the maximal flow speed captures the effect of geometry through the dependence on l, which can be estimated as \(l\sim L_c^2\left| C \right|\) for Lc<1/|C|, where C is the substrate curvature and Lc the typical cell size, and l~1/|C| for Lc>1/|C|. This predicted non-monotonic dependence on curvature is observed experimentally (Fig. 3c). Third, it is shown in the Supplementary Information that S(x) can be analytically determined, yielding a linear behaviour in the limit of a large nematic correlation length, in agreement with observations (Fig. 2e). Last, the model also predicts the observed tension anisotropy (Fig. 4f), as shown in the Supplementary Information. This theoretical analysis finally indicates that the hallmarks of the actin structure at negative curvature—tension anisotropy gradient, actin order parameter gradient, and anterograde flow—result mainly from the contractile behaviour of the cytoskeleton and of the geometry characterized by the negative curvature of the forward edge.

We next sought to find mechanisms of actin dynamics regulation different from the one previously observed in lamellipodium-based protrusions25,46. Photoconversion of mEos2-Actin (Fig. 5a–c and Supplementary Video 9) within the structure at negative curvature (see Methods) revealed that actin depolymerization increased from the rear to the front, whereas polymerization peaked in the centre of the structure behind the depolymerization region. It resulted in a local polymerization–depolymerization gradient, accompanying the anterograde actin flow and in contrast to the polymerization gradient previously described in cell protrusions at positive curvatures25 (Fig. 5d,e). Correspondingly, Arp2/3 complex was mainly localized in the transition region between radial and transverse fibres (Fig. 5f,h), whereas cofilin, an actin depolymerization factor, co-localized with the actomyosin contractile cable at the cell front (Fig. 5g,h). In addition, N-WASP protein clusters were observed in the same transition region (Supplementary Fig. 5a), where we also observed highly dynamic random motion of actin (Supplementary Fig. 5c, left panel). The inhibition of Arp2/3 activity (200 μM CK666 treatment) immediately abolished such activity (Supplementary Fig. 5c, middle panel) and eventually led to the depletion of transverse fibres, which could be rescued by CK666 washout (Supplementary Fig. 5c, right panel and Supplementary Video 10). The inhibition of the upstream regulator of the Arp2/3 complex, N-WASP, with Wiskostatin led to the same observation (Supplementary Fig. 5b). To perturb actin depolymerization, we treated cells with 1 nM Jasplakinolide, which caused the actin structure to collapse (Supplementary Fig. 5j and Supplementary Video 11), suggesting that actin turnover is important in maintaining the dynamic stability of the structure. The effect is irreversible and could not be rescued by washout.

Fig. 5: Directional actin flow is accompanied by a local polymerization–depolymerization gradient.
figure 5

a–e, Photoconversion of mEos2-actin to measure actin polymerization and depolymerization dynamics. a, Left: actin structure before photoconversion (in green) in a square region of interest (yellow dashed line); the edge of the fibronectin pattern is marked by a white dashed line. Right: actin structure immediately after photoconversion (in magenta). Scale bars, 5 μm. b, Kymograph along the white arrow in a of the green channel shows hotspots of actin polymerization. c, Kymograph along the white arrow in a of the red channel shows actin depolymerization. Horizontal scale bar, 1 μm, vertical scale bar, 10 s. d, Actin polymerization measured from photoconversion experiments (n = 47). Error bars indicate s.e.m. e, Actin depolymerization measured from photoconversion experiments (n = 47). Error bars indicate s.e.m. f, mEmerald-arp-p34 in tranfected cells shows Arp2/3 localization. Scale bar, 2 μm. g, Cofilin staining shows depolymerization activity in the front. Scale bar, 2 μm. For f and g, the white dashed line marks the edge of the fibronectin pattern and the green dashed line marks the edge of the cell. h, Polymerization–depolymerization gradient at negative curvature. n = 8 for Arp2/3 and n = 3 for cofilin. Error bars indicate s.e.m., i, GFP-FAK localizes on RFs. The magenta dashed line marks the edge of the fibronectin pattern and the green dashed line marks the edge of the cell. Scale bar, 2 μm. j, SIM-TIRF imaging of GFP-FAK near the substrate at the edge of the adhesive pattern (magenta dashed line) shows mobilization of particles of GFP-FAK on radial actin fibres. Scale bar, 2 μm. k, Kymograph along the yellow dashed line in j; the magenta dashed line marks the edge of the fibronectin (FN) pattern. GFP-FAK particles engage in continuous flow (filled arrowhead) in the non-adherent region on the left side whereas most particles stay immobile (open arrowhead) in the adherent region on the right side. Horizontal scale bar, 1 μm; vertical scale bar, 1 min. l, Schematic showing the polarized organization of the actin cytoskeleton at negative curvature.

Full size image

We then asked how Arp2/3-dependent actin polymerization could be localized to the transition region. Actin polymerization in the lamellipodia is reported to be downstream of FA signaling, where focal adhesion kinase (FAK) activates N-WASP and Arp2/347. Noticing that radial fibres were connected to FAs and also underwent anterograde flow, we hypothesized that the polymerization signal could be transported by actin flow along radial fibres from FAs to the transition region23,37,48,49. To test this, laser ablation of radial fibres was performed, Arp2/3 was subsequently recruited to the rear of the ablation site (Supplementary Fig. 5d,e and Supplementary Video 12, right panel). This was followed by local polymerization of actin, which then engaged in anterograde flow (Supplementary Fig. 5f,g and Supplementary Video 12, left panel). Hence, actin polymerization signals could be transported from the rear of the cell by the anterograde flow of radial fibres. Since the radial fibres are connected to FAs, we wondered whether the radial fibres could also mediate the transport of signalling protein complexes. Indeed, with the YFP-PBD biosensor50, we observed that the active small GTPases Rac/cdc42 can be transported forwards at negative curvature (Supplementary Fig. 5h,i). FAK localizes along radial fibres (Fig. 5i,j) and FAK clusters remained mostly stationary on fibronectin patterns (Fig. 5k, open arrowhead) but could be mobilized and then flow towards the front with the radial fibres over non-adherent regions (Fig. 5k, filled arrowhead).

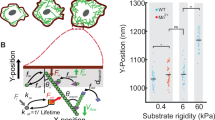
Since the polarized actin structure can form in both single cells (Supplementary Fig. 1f–h) and individual cells within an epithelial monolayer (Fig. 2a–d), we hypothesized that cell–cell junctions may enable the formation of multicellular actin structures at negative curvatures with large radii of curvature. To test this, we seeded either MDCK wild type (WT) or MDCK cells with stable α-catenin knockdown (KD) where cell–cell junctions are weakened (Fig. 6d–f)51 on fibronectin patterns with varying curvatures (Fig. 6a–f and Supplementary Fig. 6a). Both WT and α-catenin KD cells could form suspended actin structures on patterns with radii of curvature equal to or smaller than 15 μm (Fig. 6b,e). However, whereas the WT cells could form suspended multicellular actin structures connected by E-cadherin adhesions (Fig. 6c, white arrowhead) on patterns with radii of curvature from 15 to 100 μm (Supplementary Fig. 6a), α-catenin KD cells could not, and failed to extend out of the fibronectin pattern (Fig. 6f and Supplementary Fig. 6a). Laser ablation of the actin cables at the edge (Fig. 6g and Supplementary Video 13) led to their retraction, indicating that the mechanical tension exerted by the actin cables is important for the multicellular actin structures to extend over non-adherent areas. The retraction was significantly larger when the ablation was performed in the non-adherent region than when it was done in the adherent region (Fig. 6h), suggesting that the actin structures were mechanically coupled in the non-adherent region but were uncoupled in the adherent region, potentially due to the connection of actin cables to FAs in the adherent regions.

Fig. 6: Role of cell–cell junctions in curvature sensing and mechanics of actin structure.
figure 6

a–f, Cell–cell junctions are dispensable for suspended actin structure formation at small single-cell scales but indispensable at large multicellular scales. a, Image showing immunostaining of MDCK WT cells on a fibronectin pattern; E-cadherin in green and phalloidin in magenta. Scale bar, 100 μm. b, A single WT cell can form an actin suspended structure at a negative curvature with 15 μm radius. The white dashed line marks the edge of the fibronectin pattern (same for c, e and f). Scale bar, 10 μm. c, Multicellular actin structure forms at a negative curvature with 50 μm radius. Actin cables are joined by E-cadherin adhesions (filled arrowhead). Scale bar, 10 μm. d, Image showing immunostaining of α-catenin stable MDCK KD cells on a fibronectin pattern; E-cadherin in green and phalloidin in magenta. Note the weak staining of E-cadherin, indicating weakened cell–cell junctions. Scale bar, 100 μm. e, A single α-catenin KD cell can form a suspended actin structure at a negative curvature with 15 μm radius. Scale bar, 10 μm. f, α-Catenin KD cells fail to form multicellular suspended actin structures at a negative curvature with 50 μm radius. Scale bar, 10 μm. g, Image of actin structure at negative curvature (30 μm radius) before (magenta) and 10 s after (green) laser ablation of the cables outside the fibronectin pattern (at the point of the filled arrowhead), showing retraction of the actin structure. The white dashed line marks the edge of the fibronectin pattern. Scale bar, 15 μm. h, Retraction of the actin structure is significantly larger when ablating actin cables out of the fibronectin pattern than when ablating actin cables on the fibronectin pattern. Two-sided t-test was used, p = 0.000014. A normal distribution was tested and confirmed with Anderson–Darling test at 0.01 confidence interval. n = 19 for on pattern and n = 20 for out of pattern. i, MDCK monolayer cannot migrate over non-adherent circles with a diameter of 100 μm, despite their ability to extend into the non-adherent region with suspended actin structure (filled arrowheads). Scale bar, 20 μm.

Full size image

There could be a maximum non-adherent circle size beyond which the cells could not migrate over as a coherent monolayer22. Indeed, for 100-μm-diameter non-adherent circles, although the cells could occasionally extend partially into the non-adherent region with multicellular actin structures (Fig. 6l, filled arrowheads), the monolayer failed to migrate over the non-adherent circle even after 45 hours (Fig. 6l and Supplementary Video 14). On the other hand, when the size of the non-adherent pattern is small compared to the size of single cells, α-catenin KD cells could also migrate over it, albeit with less coordination compared to the WT cells (Supplementary Fig. 6b and Supplementary Video 15). These results suggest that the cell–cell junction is not required for curvature sensing and actin structure formation for single cells or individual cells in a monolayer when the radius of curvature is small, but is essential for the formation and maintenance of multicellular actin structures when the radius of curvature is larger than the size of individual cells.

Our study demonstrates that migrating cells sense large-scale curvatures through spatio-temporal adaptation of the flow and tension distribution within the actin cytoskeleton as a direct result of the physical constraint imposed by the geometry of the cell and substrate. The unique range of curvature sensing at the scale of ten to tens of micrometres (Fig. 3c) is distinct from that of molecular curvature sensors such as BAR domain proteins and septins. Nevertheless, curvature sensing mechanisms at scales beyond tens of micrometres remains elusive and may involve tissue tension sensing52. Apart from sensing the sign of the curvature, the cells also show different actin flow velocities in response to different magnitudes of curvatures (Fig. 3c). Our theoretical analysis suggests that this dependence could reflect the size of the actin structure, characterized by the length of the suspended part l, which naturally varies with the change of curvature (see model description in text and Supplementary Information).

Formins are also important actin polymerization factors; however, we did not observe noticeable differences in actin dynamics and organization when cells were treated with the formin inhibitor SMIFH2 (25 μM concentration, data not shown). Nevertheless, formins have been shown to help polymerize actin in the radial fibres30 and the difference between measured actin polymerization activity (Fig. 5d) and Arp2/3 profile (Fig. 5h) at the rear of the actin structure indicates that formins could play a minor role here. The inhibition of actin depolymerization by Jasplakinolide resulted in the rapid break-up of the actin structure. This could be due to the high contractility inside the suspended structure, which in the absence of depolymerization builds up tension inside the actin network and leads to its collapse. On the other hand, the stabilization of F-actin by Jasplakinolide treatment could also reduce the G-actin concentration in the cytosol and in turn inhibit the polymerization rate of actin53. This suggests that the active maintenance of the actin structure depends on the dynamic turnover of the cytoskeleton.

A former study showed that after laser severing of the actin cable at the edge of a MDCK monolayer, it can transform into a lamellipodial protrusion12. However, in our set-up, the actin cable could repair rapidly after laser ablation, and repeated laser ablation induced the collapse of the actin structure, which can be explained by the fact that non-adherent pattern may serve to prevent lamellipodial protrusion formation after ablation. In addition, the switching of migration mode after laser ablation of the actin cable could also be regulated by curvature. Indeed, when we ablated actin cables at the edge of a MDCK monolayer on a continuously adhesive substrate, 71% (5 out of 7) of the cells transformed into lamellipodial protrusions when the edges were of positive curvature, whereas 89% (8 out of 9) of the cells repaired the cable when the edges were of negative curvature (Supplementary Fig. 4g, Supplementary Table 1 and Supplementary Video 16).

In light of these results, curvature sensing by actin flow appears to be the fundamental mechanism of migration mode switching, although the curvature itself might be generated by diverse environmental and cellular conditions in vivo.

Methods

Cell culture, plasmids and transfection

MDCK WT, MDCK GFP actin, MDCK GFP MRLC, MDCK α-catenin KD cells were a kind gift from James Nelson. MDCK PBD YFP cell line was a gift from Fernando Martín-Belmonte50. REF52 cells, GFP-α-Actinin and mCherry-α-Actinin constructs were a gift from Alexander Bershadsky. The GFP-Talin, N-WASP-GFP and GFP-FAK constructs were a gift from Michael Sheetz. The mEos3.2-MyosinIIA-C-18, mEmerald-Myosin IIA-N, mApple-Myosin IIA-N, ARP-p34-N-mEmerald, mEos2-Actin-C-18, mEmerald-Actin-C-18 and mEmerald-ARPp34-N-14 constructs were from Michael Davidson reserve and kindly distributed by Pakorn Kanchanawong.

Cells were cultured in Dulbecco modified Eagle medium (DMEM; Invitrogen) supplied with 10% foetal bovine serum (FBS; Invitrogen) and changed to Leibovitz imaging medium (Invitrogen) supplied with 10% FBS before imaging.

Transfection of plasmids was performed with a Neon electroporation system (Invitrogen) as per the manufacturer’s instructions.

Drug treatment

Drug treatments were performed on stage by exchanging normal imaging medium with the same amount of medium containing drugs pre-warmed to 37 °C. Concentrations of drugs used were as follows: (-) Blebbistatin (Selleckchem) 25 μM, CK666 (Millipore) 200 μM, Wiskostatin (Sigma) 50 μM, Jasplakinolide (Sigma) 1 nM. Washout of drugs was performed on stage by rinsing with 10 ml imaging medium three times. The interval between consecutive time-lapse imagings due to drug addition or washout is generally between 5 min to 10 min.

Model wound closure assay and MDCK monolayer expansion assay

Model wound closure experiments were performed on a continuous fibronectin-coated substrate as described before2,27 with a flower-shaped block to induce positive and negative curvatures at the edge of the gap. Cells were fixed 15 min after the removal of the block, followed by immunostaining. For the freely expanding MDCK monolayer assay, a rectangular PDMS (Sylgard 184, Dow Corning) block (approximately 0.5 cm by 1 cm) was placed in the centre of the dish and MDCK cells were allowed to grow to confluence around the block before the block was removed and the expansion of the monolayer into the empty space was initiated. Images in Fig. 1a,b were taken approximately 10 hours after the removal of the block.

Micropatterning of glass substrate

Silicon wafers with custom-designed micro patterns were made with soft-lithography. PDMS pillars were cast from the wafers and used to pattern glass surfaces to make islands of fibronectin (20 μg ml−1 human plasma fibronectin mixed with 1–5% Atto-674 conjugated fibronectin in Milli-Q water) surrounded by PLL-g-PEG (1 mg ml−1 PLL(20)-g[3.5]- PEG(2), SuSoS, dissolved in phosphate-buffered saline (PBS)) with a modified protocol based on plasma microcontact patterning (PμCP)54. Briefly, PDMS pillars were placed with their features down in contact with glass, and the unblocked part of the glass was activated with a low-power oxygen plasma (Harrick Plasma) for 20 min. Then 20 μl of PLL-g-PEG solution was added and incubated at room temperature for one hour, after which the stencil was removed vertically with tweezers and the glass was rinsed once with Milli-Q water to remove the excess PLL-g-PEG. Then, fibronectin solution was added to coat the previously blocked surface at 37 °C for 30 min and rinsed three times with Milli-Q water. Cells were then seeded on the patterned substrate and allowed to attach for 30–35 mins, rinsed with DMEM to remove unattached cells, and imaged the following day. Patterns with near-confluent colonies were selected for imaging to minimize movement of cells within patterns as well as over-crowding effects.

Immunostaining and image acquisition

Actin filaments were stained with Alexa Fluor 568 Phalloidin (Life Technologies). Myosin IIA was stained with either Rabbit Anti-Myosin IIA (Sigma M8064) or Mouse anti Myosin IIA (abcam ab55456). Paxillin was stained with Rabbit Monoclonal anti-Paxillin [Y113] (abcam ab32084). Cofilin was stained with Rabbit anti cofilin (abcam ab11062). E-cadherin was stained with Rat anti E-cadherin (Sigma U3254). Secondary antibodies used were Alexa Fluor 488 goat anti rabbit (Life Technologies A11011), Alexa Fluor 568 Goat anti Rabbit (Life Technologies A11008), Alexa Fluor 488 Goat anti Mouse (Life Technologies A11001), Alexa Fluor 568 Goat anti-Mouse (Life Technologies A11004), Alexa Fluor 488 Donkey anti Rat (Life Technologies A21208).

Cells were fixed with either methanol at −20 °C for cofilin or with 4% paraformaldehyde (PFA) at 37 °C for others, permeablized with 0.2% Triton X-100 in Tris-buffered saline (TBS), blocked with 1% BSA in TBS and stained with the aforementioned antibodies. Quantitative imaging was performed on a Nikon A1R scanning confocal microscope with either a 1.27 NA (numerical aperture) 60× water immersion objective or a 1.49 NA 100× oil immersion objective. For E-cadherin staining, images were taken with an Olympus spinning disk confocal microscope with a super-resolution module installed (1.49 NA 100× objective).

Structure illumination microscopy

Live and fixed sample SIM imaging was performed on a Nikon NSIM microscope with a 1.49 NA oil immersion objective. For slow dynamics of transverse fibre flow, cells were imaged with 100 ms exposure and 1 to 2 min per frame. For fast dynamics of actin, cells were imaged with 30–50 ms exposure and 10–15 s per frame. Image reconstruction was done with the NIS Elements software as per the manufacturer’s instructions.

Particle image velocimetry (PIV) analysis

Velocity measurement of myosin flow at different negative curvature patterns was performed by imaging cells transfected with mEos3.2 Myosin IIA. Before the acquisition, a 405 nm laser was used to photo-switch a fraction of the fluorophores from green to red fluorescence, such that the images of Myosin IIA exhibit locally distinctive patterns that can be tracked by the image cross-correlation through PIV. Images were acquired with a Nikon NSTORM microscope in total internal reflection fluorescence (TIRF) mode with a 1.49 NA 100× oil immersion objective. The open source software MatPIV was used to process the images with a 16-by-16 pixel sampling window and 75% overlap. The results were further passed through a median filter to reduce noise. A custom-written MATLAB (Mathworks) code was used to define an analysis region of interest in the centre of the actin structure for each experiment and average the signal over space and time to produce the mean radial flow velocity. Outliers, defined as three times the standard deviation from the medium, were removed.

Fluorescent speckle microscopy

Cells were transfected with a low concentration of mEmerald-actin plasmid (0.1 μg DNA for a 100 μl electroporation experiment) and imaged on a Nikon Nstorm microscope with a 1.49 NA 100× oil immersion objective with TIRF illumination. Images were acquired with 500 ms exposure and a frame rate of 3 s per frame to measure the flow of actin. Images were processed with the openly available quantitative fluorescent speckle microscopy (QFSM) software provided by Gaudenz Danuser‘s lab55, to measure the flow velocity. Then the output data was collected and analysed to compute the averaged radial velocity with MATLAB.

Laser ablation

An ultraviolet laser (355 nm, 300 ps pulse duration, 1 kHz repetition rate, PowerChip PNV-0150-100, Team Photonics) was interfaced to a Nikon A1R MP confocal microscope. The ultraviolet laser was integrated into a Nikon ECLIPSE Ti microscope body through a customized optical path and a customized dichroic filter, and were co-aligned with the optical axis of the microscope. The position of the laser was controlled by a mirror mounted on two linear actuators (TRA12CC, Newport), and the exposure time of the laser was controlled by a mechanical shutter (VS25S2ZM0, Uniblitz). The actuators (through the actuator controller, ESP301-3G, Newport) and shutter were controlled by custom ImageJ plug-ins from a PC. The laser ablation system, which is independent of the imaging microscope, allows us to perform an ablation during imaging. MDCK GFP MRLC cells were used and for measurement of tension anisotropy, a point ablation (with a laser power of 25nW at the back aperture of the objective, 300 ms duration) was performed at different positions within the myosin-rich region. Images were then analysed with a custom-written MATLAB code to calculate the recoil in radial and transverse direction 5 s after the ablation. The relative distance of the ablation site was calculated with respect to the rear of the region as 0 and to front of it as 1. For ablation of TFs or RFs, a region of imterest line was drawn and a line ablation was performed during continuous image acquisition. For measurement of actin structure retraction after laser ablation of actin cables either on or out of the fibronectin pattern, a point ablation was performed to sever the actin cables at different locations and a custom-written MATLAB code was used to calculate the retraction distance, which was defined by dbefore−dafter, where dbefore and dafter are the furthest distance from the edge of the cell to the fibronectin pattern before and 10 s after the ablation.

Traction force microscopy

Traction force microscopy was performed as described before22 with some modifications, using soft PDMS gels (1:1 mixture of CY52-276A and CY52-276B (Dow Corning Toray) resulting in an elastic modulus of ~8 kPa) spin-coated (700 rpm) on glass bottom dishes (Iwaki) and cured at 80 °C for two hours. The substrate was then functionalized with 5% aminopropyl triethoxysilane (Sigma) in methanol for 5 min, rinsed three times with ethanol, and cured at 80 °C for 20 min. Then a diluted (1:500) solution of 100 nm carboxylated red fluorescent beads (Invitrogen) in Milli-Q water was added, incubated for 15 min and rinsed four times with Milli-Q water to remove excessive beads. For fibronectin patterning of the gel, PDMS (Sylgard 184, Dow Corning) stencils with pillars of the given shapes were treated with ultraviolet for 20 min and coated with a solution of 50 μg ml−1 human plasma fibronectin mixed with 10% Atto647 conjugated fibronectin in Milli-Q water for one hour. Afterwards, the solution was removed with suction and the stencil was inverted and directly stamped on a previously prepared polyvinyl alcohol (PVA) membrane (Sigma). Then the PVA membrane was gently placed face down on the soft PDMS substrate. After one hour, a 0.2% solution of Pluronics F-127 (Sigma) in Milli-Q water was added to dissolve the PVA and block the uncoated area.

Cells were then seeded on the patterned substrate, allowed to attach for one hour, rinsed with DMEM to remove unattached cells, and imaged on a Zeiss LSM780 confocal microscope with a 1.2 N.A. 60× water immersion objective the next day. After live imaging, a 1% SDS solution in PBS was added to lyse the cells and a resting beads image (null-force) was captured.

Analysis of traction forces based on bead displacement was performed as described previously39.

Measurement of actin polymerization and depolymerization by photoconversion

Cells were first transfected with mEos2-Actin-C-18 construct and seeded on the patterns. We performed photoconversion of mEos2-Actin within the structure at negative curvature with a 405 nm laser in a rectangular region of interest to measure the polymerization and depolymerization dynamics (Fig. 5a and Supplementary Video 9). After the photoconversion, hotspots of fluorescence in the green channel reappeared within the centre region at negative curvature in the green channel, suggesting newly polymerized actin filaments (Fig. 5b). In the meantime, decreasing fluorescence in the red channel was driven by depolymerization of actin filaments (Fig. 5c). Actin polymerization and depolymerization measurements based on photoconversion experiments are calculated as follows: polymerization is computed as the local average of fluorescence intensity between 20–40 s after photoconversion minus the fluorescence intensity before photoconversion in the green channel, normalized by the difference between the fluorescence intensity immediately before and after photoconversion; depolymerization is computed as the local average of the fluorescence intensity between 20–40 s after photoconversion subtracted from the fluorescence intensity immediately after photoconversion in the red channel, normalized by the difference between the fluorescence intensity immediately before and after photoconversion. Assuming photobleaching is independent of the spatial location, there is no need to correct for photobleaching to compare the relative values between different spatial locations. We do not claim that the numerical values obtained from this measurement necessarily represent a linear mapping to the molecules of actin monomers incorporated into F-actin per unit time.

Image processing and analysis

Images shown in the figures were background subtracted and contrast enhanced for visualization. Intensity measurements were performed on raw images. Due to the nonlinearity of SIM images, only confocal images were used for intensity measurements, hence only structural but not intensity information should be interpreted from the SIM images.

Due to the 3D shape of the cell, intensity measurements over the whole actin structure were done by taking a 2 μm z-stack and averaging along the z direction after segmentation of each slice to calculate the local fluorescence concentration, except for live imaging experiments where high time resolution is needed and a single slice was taken but with a larger pinhole size to image the entire structure.

Profiles with relative distances were calculated by measuring the intensity at each point within a central region at positive or negative curvature, and its position along the radial direction (perpendicular to the edge of the fibronectin pattern), taking the rear of the radial fibres as 0 and the frontal edge of the cell as 1.

Fibre orientation analysis was performed with a custom-written MATLAB code to measure the local fibre orientation based on edge-detection of F-actin images. The order parameter was then calculated as S = <cos(2θ) >, where θ is the angle at each point between the actin fibre and the radial direction.

Actin dynamics index (ADI) is measured by taking a time-lapse (15 s per frame) movie of GFP actin with live SIM microcopy, and calculated as ADI(i) = (I(i) − I(i − 1))/std(I(i)), with the image of frame i as I(i) and the standard deviation of frame i as std(I(i)). An averaged ADI for all frames is shown in the figures.