Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Scalable spin squeezing from finite-temperature easy-plane magnetism

Nature Physics volume 20, pages 1575–1581 (2024)Cite this article

Subjects

Abstract

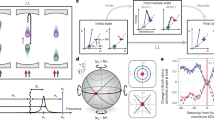
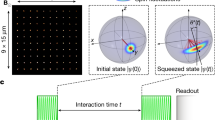
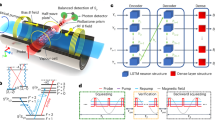
Spin squeezing is a form of entanglement that reshapes the quantum projection noise to improve measurement precision. Here, we provide numerical and analytic evidence for the following conjecture: any Hamiltonian exhibiting finite-temperature easy-plane ferromagnetism can be used to generate scalable spin squeezing, thereby enabling quantum-enhanced sensing. Our conjecture is guided by a connection between the quantum Fisher information of pure states and the spontaneous breaking of a continuous symmetry. We demonstrate that spin squeezing exhibits a phase diagram with a sharp transition between scalable squeezing and non-squeezing. This transition coincides with the equilibrium phase boundary for XY order at a finite temperature. In the scalable squeezing phase, we predict a sensitivity scaling that lies between the standard quantum limit and the scaling achieved in all-to-all coupled one-axis twisting models. A corollary of our conjecture is that short-ranged versions of two-axis twisting cannot yield scalable metrological gain. Our results provide insights into the landscape of Hamiltonians that can be used to generate metrologically useful quantum states.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Scalable spin squeezing from easy-plane ferromagnetism.
Fig. 2: Dynamics of easy-plane order and squeezing.
Fig. 3: Impact of finite temperature on squeezing.

Similar content being viewed by others

Data availability

Source data and analysis code is available via the Harvard Dataverse at https://doi.org/10.7910/DVN/XIM8YU.

Code availability

Code for numerical simulations is available from the corresponding author upon request.

References

  1. Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).

    ADS  Google Scholar 

  2. Degen, C., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).

    MathSciNet  ADS  Google Scholar 

  3. Schnabel, R., Mavalvala, N., McClelland, D. E. & Lam, P. K. Quantum metrology for gravitational wave astronomy. Nat. Commun. 1, 121 (2010).

    ADS  Google Scholar 

  4. Wasilewski, W. et al. Quantum noise limited and entanglement-assisted magnetometry. Phys. Rev. Lett. 104, 133601 (2010).

    ADS  Google Scholar 

  5. Leibfried, D. et al. Toward Heisenberg-limited spectroscopy with multiparticle entangled states. Science 304, 1476–1478 (2004).

    ADS  Google Scholar 

  6. Bouwmeester, D., Pan, J.-W., Daniell, M., Weinfurter, H. & Zeilinger, A. Observation of three-photon Greenberger−Horne−Zeilinger entanglement. Phys. Rev. Lett. 82, 1345–1349 (1999).

    MathSciNet  ADS  Google Scholar 

  7. Pan, J.-W., Bouwmeester, D., Daniell, M., Weinfurter, H. & Zeilinger, A. Experimental test of quantum nonlocality in three-photon Greenberger−Horne−Zeilinger entanglement. Nature 403, 515–519 (2000).

    ADS  Google Scholar 

  8. Omran, A. et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 365, 570–574 (2019).

    MathSciNet  ADS  Google Scholar 

  9. Pogorelov, I. et al. Compact ion-trap quantum computing demonstrator. PRX Quantum 2, 020343 (2021).

    ADS  Google Scholar 

  10. Jones, J. A. et al. Magnetic field sensing beyond the standard quantum limit using 10-spin NOON states. Science 324, 1166–1168 (2009).

    ADS  Google Scholar 

  11. Dicke, R. H. Coherence inspontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).

    ADS  Google Scholar 

  12. Pezzè, L., Smerzi, A., Oberthaler, M. K., Schmied, R. & Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).

    MathSciNet  ADS  Google Scholar 

  13. Wieczorek, W. et al. Experimental entanglement of a six-photon symmetric Dicke state. Phys. Rev. Lett. 103, 020504 (2009).

    ADS  Google Scholar 

  14. Lücke, B. et al. Detecting multiparticle entanglement of Dicke states. Phys. Rev. Lett. 112, 155304 (2014).

    ADS  Google Scholar 

  15. Zou, Y.-Q. et al. Beating the classical precision limit with spin-1 Dicke states of more than 10,000 atoms. Proc. Natl Acad. Sci. USA 115, 6381–6385 (2018).

    ADS  Google Scholar 

  16. Kitagawa, M. & Ueda, M. Squeezed spin states. Phys. Rev. A 47, 5138–5143 (1993).

    ADS  Google Scholar 

  17. Wineland, D. J., Bollinger, J. J., Itano, W. M. & Heinzen, D. J. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A 50, 67–88 (1994).

    ADS  Google Scholar 

  18. Hosten, O., Engelsen, N. J., Krishnakumar, R. & Kasevich, M. A. Measurement noise 100 times lower than the quantum-projection limit using entangled atoms. Nature 529, 505–508 (2016).

    ADS  Google Scholar 

  19. Estève, J., Gross, C., Weller, A., Giovanazzi, S. & Oberthaler, M. K. Squeezing and entanglement in a Bose−Einstein condensate. Nature 455, 1216–1219 (2008).

    ADS  Google Scholar 

  20. Appel, J. et al. Mesoscopic atomic entanglement for precision measurements beyond the standard quantum limit. Proc. Natl Acad. Sci. USA 106, 10960–10965 (2009).

    ADS  Google Scholar 

  21. Muessel, W., Strobel, H., Linnemann, D., Hume, D. & Oberthaler, M. Scalable spin squeezing for quantum-enhanced magnetometry with Bose−Einstein condensates. Phys. Rev. Lett. 113, 103004 (2014).

    ADS  Google Scholar 

  22. Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).

    MathSciNet  ADS  Google Scholar 

  23. Deutsch, J. M. Quantum statistical mechanics in a closed system. Phys. Rev. A 43, 2046–2049 (1991).

    ADS  Google Scholar 

  24. Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 50, 888–901 (1994).

    ADS  Google Scholar 

  25. Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854–858 (2008).

    ADS  Google Scholar 

  26. Hauke, P., Heyl, M., Tagliacozzo, L. & Zoller, P. Measuring multipartite entanglement through dynamic susceptibilities. Nat. Phys. 12, 778–782 (2016).

    Google Scholar 

  27. Gabbrielli, M., Smerzi, A. & Pezzè, L. Multipartite entanglement at finite temperature. Sci. Rep. 8, 15663 (2018).

    ADS  Google Scholar 

  28. Chen, C. et al. Continuous symmetry breaking in a two-dimensional Rydberg array. Nature 616, 691–695 (2023).

    ADS  Google Scholar 

  29. Comparin, T., Mezzacapo, F. & Roscilde, T. Multipartite entangled states in dipolar quantum simulators. Phys. Rev. Lett. 129, 150503 (2022).

    ADS  Google Scholar 

  30. Perlin, M. A., Qu, C. & Rey, A. M. Spin squeezing with short-range spin-exchange interactions. Phys. Rev. Lett. 125, 223401 (2020).

    ADS  Google Scholar 

  31. Comparin, T., Mezzacapo, F. & Roscilde, T. Robust spin squeezing from the tower of states of U(1)-symmetric spin hamiltonians. Phys. Rev. A 105, 022625 (2022).

    MathSciNet  ADS  Google Scholar 

  32. Comparin, T., Mezzacapo, F., Robert-de Saint-Vincent, M. & Roscilde, T. Scalable spin squeezing from spontaneous breaking of a continuous symmetry. Phys. Rev. Lett. 129, 113201 (2022).

    ADS  Google Scholar 

  33. Halperin, B. I. & Hohenberg, P. C. Hydrodynamic theory of spin waves. Phys. Rev. 188, 898–918 (1969).

    ADS  Google Scholar 

  34. Cappellaro, P. & Lukin, M. D. Quantum correlation in disordered spin systems: applications to magnetic sensing. Phys. Rev. A 80, 032311 (2009).

    ADS  Google Scholar 

  35. Davis, E. J. et al. Protecting spin coherence in a tunable Heisenberg model. Phys. Rev. Lett. 125, 060402 (2020).

    ADS  Google Scholar 

  36. Kwasigroch, M. P. & Cooper, N. R. Bose−Einstein condensation and many-body localization of rotational excitations of polar molecules following a microwave pulse. Phys. Rev. A 90, 021605 (2014).

    ADS  Google Scholar 

  37. Kwasigroch, M. P. & Cooper, N. R. Synchronization transition in dipole-coupled two-level systems with positional disorder. Phys. Rev. A 96, 053610 (2017).

    ADS  Google Scholar 

  38. Rey, A. M., Jiang, L., Fleischhauer, M., Demler, E. & Lukin, M. D. Many-body protected entanglement generation in interacting spin systems. Phys. Rev. A 77, 052305 (2008).

    ADS  Google Scholar 

  39. Davis, E. J. et al. Probing many-body noise in a strongly interacting two-dimensional dipolar spin system. Nat. Phys. 19, 836–844 (2023).

    Google Scholar 

  40. Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).

    ADS  Google Scholar 

  41. Gross, C. & Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 357, 995–1001 (2017).

    ADS  Google Scholar 

  42. Ni, K.-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008).

    ADS  Google Scholar 

  43. Chomaz, L. et al. Long-lived and transient supersolid behaviors in dipolar quantum gases. Phys. Rev. X 9, 021012 (2019).

    Google Scholar 

  44. Tran, T. T., Bray, K., Ford, M. J., Toth, M. & Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 11, 37–41 (2016).

    ADS  Google Scholar 

  45. Bruno, P. Absence of spontaneous magnetic order at nonzero temperature in one- and two-dimensional heisenberg and XY systems with long-range interactions. Phys. Rev. Lett. 87, 137203 (2001).

    ADS  Google Scholar 

  46. Maghrebi, M. F., Gong, Z.-X. & Gorshkov, A. V. Continuous symmetry breaking in 1D long-range interacting quantum systems. Phys. Rev. Lett. 119, 023001 (2017).

    MathSciNet  ADS  Google Scholar 

  47. Schachenmayer, J., Pikovski, A. & Rey, A. M. Many-body quantum spin dynamics with monte carlo trajectories on a discrete phase space. Phys. Rev. X 5, 011022 (2015).

    Google Scholar 

  48. Hauschild, J. & Pollmann, F. Efficient numerical simulations with tensor networks: Tensor Network Python (TeNPy). SciPost Physics Lecture Notes 005 https://scipost.org/10.21468/SciPostPhysLectNotes.5 (2018).

  49. Macrì, T., Smerzi, A. & Pezzè, L. Loschmidt echo for quantum metrology. Phys. Rev. A 94, 010102 (2016).

    ADS  Google Scholar 

  50. Davis, E., Bentsen, G. & Schleier-Smith, M. Approaching the Heisenberg limit without single-particle detection. Phys. Rev. Lett. 116, 053601 (2016).

    ADS  Google Scholar 

  51. Colombo, S. et al. Time-reversal-based quantum metrology with many-body entangled states. Nat. Phys. 18, 925–930 (2022).

    Google Scholar 

  52. Yan, B. et al. Observation of dipolar spin-exchange interactions with lattice-confined polar molecules. Nature 501, 521–525 (2013).

    ADS  Google Scholar 

  53. de Léséleuc, S., Barredo, D., Lienhard, V., Browaeys, A. & Lahaye, T. Optical control of the resonant dipole−dipole interaction between Rydberg atoms. Phys. Rev. Lett. 119, 053202 (2017).

    ADS  Google Scholar 

  54. Gottscholl, A. et al. Initialization and read-out of intrinsic spin defects in a van der Waals crystal at room temperature. Nat. Mater. 19, 540–545 (2020).

    ADS  Google Scholar 

  55. Chejanovsky, N. et al. Single-spin resonance in a van der Waals embedded paramagnetic defect. Nat. Mater. 20, 1079–1084 (2021).

    ADS  Google Scholar 

  56. Eichhorn, T. R., McLellan, C. A. & Bleszynski Jayich, A. C. Optimizing the formation of depth-confined nitrogen vacancy center spin ensembles in diamond for quantum sensing. Phys. Rev. Mater. 3, 113802 (2019).

    Google Scholar 

  57. Smith, J. M., Meynell, S. A., Bleszynski Jayich, A. C. & Meijer, J. Colour centre generation in diamond for quantum technologies. Nanophotonics 8, 1889–1906 (2019).

    Google Scholar 

  58. Tasaki, H. Long-range order, ‘tower’ of states, and symmetry breaking in lattice quantum systems. J. Stat. Phys. 174, 735–761 (2019).

    MathSciNet  ADS  Google Scholar 

  59. Deutsch, J. M. Eigenstate thermalization hypothesis. Rep. Prog. Phys. 81, 082001 (2018).

    MathSciNet  ADS  Google Scholar 

  60. D’Alessio, L., Kafri, Y., Polkovnikov, A. & Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 65, 239 (2016).

  61. Defenu, N. et al. Long-range interacting quantum systems. Rev. Mod. Phys. 95, 035002 (2023).

    MathSciNet  ADS  Google Scholar 

  62. Altman, E. et al. Quantum simulators: architectures and opportunities. PRX Quantum 2, 017003 (2021).

    Google Scholar 

  63. Roscilde, T., Mezzacapo, F. & Comparin, T. Spin squeezing from bilinear spin-spin interactions: two simple theorems. Phys. Rev. A 104, L040601 (2021).

    MathSciNet  ADS  Google Scholar 

  64. Hohenberg, P. C. & Halperin, B. I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435–479 (1977).

    ADS  Google Scholar 

  65. Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. SciPost Phys. Codebases 4 https://scipost.org/10.21468/SciPostPhysCodeb.4 (2022).

  66. Gaenko, A. et al. Updated core libraries of the ALPS project. Comput. Phys. Commun. 213, 235–251 (2017).

    ADS  Google Scholar 

  67. Frérot, I., Naldesi, P. & Roscilde, T. Entanglement and fluctuations in the XXZ model with power-law interactions. Phys. Rev. B 95, 245111 (2017).

    ADS  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge the insights of E. Altman, J. Moore, M. Zaletel, C. Laumann and F. Machado. This work was support by the Army Research Office via grant no. W911NF-21-1-0262 and through the MURI program (grant no. W911NF-20-1-0136), and by the US Department of Energy via BES grant no. DE-SC0019241 and via the National Quantum Information Science Research Centers, Quantum Systems Accelerator (QSA). E.J.D. acknowledges support from the Miller Institute for Basic Research in Science. M.B. acknowledges support through the Department of Defense through the National Defense Science and Engineering Graduate Fellowship Program. B.R. acknowledges support from a Harvard Quantum Initiative postdoctoral fellowship. S.C. acknowledges support from the National Science Foundation Graduate Research Fellowship under grant no. DGE 2140743. L.P. acknowledges support from FP7/ERC consolidator grant QSIMCORR, no. 771891 and the Deutsche Forschungsgemeinschaft (German Research Foundation) under Germany’s Excellence Strategy – EXC-2111 – 390814868, as well as the Munich Quantum Valley, which is supported by the Bavarian State government with funds from the Hightech Agenda Bayern Plus. N.Y.Y. acknowledges support from a Simons Investigator award. Matrix-product-state simulations make use of the TenPy and ITensor libraries48,65, and quantum-Monte-Carlo simulations make use of the ALPSCore libraries66.

Author information

Author notes

  1. These authors contributed equally: Maxwell Block, Bingtian Ye.

Authors and Affiliations

  1. Department of Physics, Harvard University, Cambridge, MA, USA

    Maxwell Block, Bingtian Ye, Brenden Roberts, Sabrina Chern, Bertrand I. Halperin & Norman Y. Yao

  2. Department of Physics, University of California, Berkeley, CA, USA

    Weijie Wu, Zilin Wang, Emily J. Davis & Norman Y. Yao

  3. Arnold Sommerfeld Center for Theoretical Physics, University of Munich, Munich, Germany

    Lode Pollet

  4. Munich Center for Quantum Science and Technology, Munich, Germany

    Lode Pollet

Authors
  1. Maxwell Block
    View author publications

    Search author on:PubMed Google Scholar

  2. Bingtian Ye
    View author publications

    Search author on:PubMed Google Scholar

  3. Brenden Roberts
    View author publications

    Search author on:PubMed Google Scholar

  4. Sabrina Chern
    View author publications

    Search author on:PubMed Google Scholar

  5. Weijie Wu
    View author publications

    Search author on:PubMed Google Scholar

  6. Zilin Wang
    View author publications

    Search author on:PubMed Google Scholar

  7. Lode Pollet
    View author publications

    Search author on:PubMed Google Scholar

  8. Emily J. Davis
    View author publications

    Search author on:PubMed Google Scholar

  9. Bertrand I. Halperin
    View author publications

    Search author on:PubMed Google Scholar

  10. Norman Y. Yao
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.B., B.Y., E.J.D., B.I.H. and N.Y.Y. developed and formalized the theoretical framework. M.B., B.Y., B.R. and B.I.H. performed the analytic calculations. M.B., B.Y., S.C., W.W. and Z.W. developed and performed the numerical simulations for the dynamics. L.P., M.B. and B.R. developed and performed the numerical simulations for the equilibrium phase diagrams. L.P. performed the quantum Monte Carlo analysis. B.I.H. and N.Y.Y. supervised the project. M.B., B.Y., B.I.H. and N.Y.Y. wrote the manuscript with input from all authors.

Corresponding author

Correspondence to Norman Y. Yao.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Michael Perlin and the other, anonymous, reviewer for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Dynamics of Conditional Variance.

Demonstration of long-time linear growth of Var[Y∣Z]. Large-scale (N = 1600, 2400) DTWA results up to times t ~ 50 (blue) show consistent linear growth as predicted by hydrodynamics. Exact simulations of small systems using Krylov subspace methods (red) give almost identical results at intermediate times. At later times, the exact results differ from the hydrodynamic expectation due to strong finite size effects arising from coherences between states of adjacent magnetization sectors.

Extended Data Fig. 2 Two-axis twisting (TAT).

A comparison of TAT dynamics in all-to-all (a) vs power-law interacting (b) systems. The power-law generalization of the TAT model does not enable scalable spin squeezing. Here, the initial state \(\left\vert x\right\rangle\) is simply at too high a temperature for \({{\mathbb{Z}}}_{2}\) order, preventing any quantum enhancement of the QFI. However, we emphasize, as discussed in the Methods, lowering the temperature of the initial state would not restore spin squeezing.

Extended Data Fig. 3 QFI of Thermal and Quenched States.

A comparison between the QFI density of the thermal density matrix (blue) and of a product state evolving after a quench (at the same energy density, red) for three models (from left to right): a d = 1 spin-\(\frac{1}{2}\) a long-range XX model (α = 1.7, Jz = 0, J⊥ = − 1.0, N = [6, 9, 12]), a spin-1 version of the same model (N = [3, 5, 7]) and a d = 1 spin-\(\frac{1}{2}\) a long-range Ising model (α = 1.3, Jz = − 1.0, g = 0.7, N = [4, 6, 8]). The top row shows the maximum QFI of the product state under quench dynamics as function of system size; the bottom row shows the corresponding dynamics, with opacity indicating system size. In all three cases we observe the thermal density matrix has constant QFI density while the peak dynamical QFI scales at the Heisenberg limit. This illustrates the fundamental difference between between the metrological utility of equilibrium states vs quench dynamics. In the case of the Ising model, the dynamical QFI of the Ztot operator is compared with the thermal QFI of the Xtot operator, since the thermal QFI of Ztot is negligible.

Extended Data Fig. 4 1D Squeezing Dynamics.

Squeezing as a function of time from DTWA simulations for d = 1 N = [120…10379]. Opacity increases with system size. Circular markers indicate the characteristic squeezing \({\xi }_{{{{\rm{opt}}}}}^{\;2}\) determined via the technique described in the Methods.

Extended Data Fig. 5 2D Squeezing Dynamics.

Squeezing as a function of time from DTWA simulations for d = 2 L = [11…102]. Opacity increases with system size. Circular markers indicate the characteristic squeezing \({\xi }_{{{{\rm{opt}}}}}^{\;2}\) determined via the technique described in the Methods.

Extended Data Fig. 6 3D Squeezing Dynamics.

Squeezing as a function of time from DTWA simulations for d = 3 with nearest-neighbor interactions for L = [5…50]. Opacity increases with system size. Circular markers indicate the characteristic squeezing \({\xi }_{{{{\rm{opt}}}}}^{\;2}\) determined via the technique described in the Methods.

Extended Data Fig. 7 Onset of Scalable Squeezing.

(a) Squeezing scaling exponents ν (red) and μ (blue) as functions of Jz for varying α in d = 1 presented as average values over 25 resamples of DTWA results ± SD. Estimates of the onset of each exponent are marked by ‘ + ’. The estimates are obtained by fitting μ(Jz), ν(Jz) for each resample with logistic curves. The left elbow of each logistic provides an estimate of the critical point. These estimates are superimposed on a logistic fit of average μ, ν. The estimates of the squeezing critical point fall in a broad but consistent region that tracks the thermal critical point (Fig. 1). (b) Analogous results for d = 2.

Extended Data Table 1 Order and QFI
Full size table

Supplementary information

Supplementary Information

Supplementary Figs. 1–4 and discussion of determining equilibrium critical points and benchmarking the DTWA.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Block, M., Ye, B., Roberts, B. et al. Scalable spin squeezing from finite-temperature easy-plane magnetism. Nat. Phys. 20, 1575–1581 (2024). https://doi.org/10.1038/s41567-024-02562-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02562-5

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing