Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A link between anomalous viscous loss and the boson peak in soft jammed solids

Nature Physics volume 21, pages 262–268 (2025)Cite this article

Subjects

Abstract

Understanding the mechanical properties of soft jammed solids that consist of densely packed particles, such as foams and emulsions, requires insights into the microscopic origins of linear viscoelasticity—how a solid responds to an infinitesimal deformation. Here we perform microrheology experiments on concentrated emulsions and measure the storage and loss moduli for a wide range of frequencies. We applied a linear response formalism for microrheology to a soft sphere model that undergoes the jamming transition. We find that the theory quantitatively explains the experiments. Our analysis reveals that the anomalous viscous loss seen in emulsions results from the boson peak, which is a universal vibrational property of amorphous solids and reflects the marginal stability in soft jammed solids. We show that the anomalous viscous loss is universal in systems with various interparticle interactions as it stems from the universal boson peak; it even survives below the jamming density at which thermal fluctuation is pronounced and the dynamics becomes inherently nonlinear.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Link between vibration and linear viscoelasticity revealed in this work.
Fig. 2: Complex modulus of the concentrated emulsions obtained by the microrheology experiments.
Fig. 3: Direct comparison between theory and experiment.
Fig. 4: Scaling analysis of the experimentally measured complex modulus.
Fig. 5: Anomalous viscous loss in varieties of models.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

Code availability

The computer codes used in this study are available from the corresponding authors upon reasonable request.

References

  1. Bonn, D., Denn, M. M., Berthier, L., Divoux, T. & Manneville, S. Yield stress materials in soft condensed matter. Rev. Mod. Phys. 89, 035005 (2017).

    ADS  Google Scholar 

  2. Morris, J. F. Shear thickening of concentrated suspensions: recent developments and relation to other phenomena. Annu. Rev. Fluid Mech. 52, 121–144 (2020).

    ADS  MathSciNet  MATH  Google Scholar 

  3. Behringer, R. P. & Chakraborty, B. The physics of jamming for granular materials: a review. Rep. Prog. Phys. 82, 012601 (2018).

    ADS  MATH  Google Scholar 

  4. Larson, R. The Structure and Rheology of Complex Fluids (Oxford Univ. Press, 1999).

  5. Mason, T. G. & Weitz, D. A. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 74, 1250–1253 (1995).

    ADS  MATH  Google Scholar 

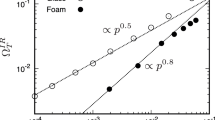
  6. Liu, A. J., Ramaswamy, S., Mason, T. G., Gang, H. & Weitz, D. Anomalous viscous loss in emulsions. Phys. Rev. Lett. 76, 3017–3020 (1996).

    ADS  Google Scholar 

  7. Cohen-Addad, S., Hoballah, H. & Höhler, R. Viscoelastic response of a coarsening foam. Phys. Rev. E 57, 6897–6901 (1998).

    ADS  MATH  Google Scholar 

  8. Hebraud, P., Lequeux, F. & Palierne, J.-F. Role of permeation in the linear viscoelastic response of concentrated emulsions. Langmuir 16, 8296–8299 (2000).

    MATH  Google Scholar 

  9. Gopal, A. & Durian, D. J. Relaxing in foam. Phys. Rev. Lett. 91, 188303 (2003).

    ADS  MATH  Google Scholar 

  10. Bandyopadhyay, R., Liang, D., Harden, J. L. & Leheny, R. L. Slow dynamics, aging, and glassy rheology in soft and living matter. Solid State Commun. 139, 589–598 (2006).

    ADS  Google Scholar 

  11. Marze, S., Langevin, D. & Saint-Jalmes, A. Aqueous foam slip and shear regimes determined by rheometry and multiple light scattering. J. Rheol. 52, 1091–1111 (2008).

    ADS  Google Scholar 

  12. Besson, S., Debregeas, G., Cohen-Addad, S. & Höhler, R. Dissipation in a sheared foam: from bubble adhesion to foam rheology. Phys. Rev. Lett. 101, 214504 (2008).

    ADS  MATH  Google Scholar 

  13. Krishan, K., Helal, A., Höhler, R. & Cohen-Addad, S. Fast relaxations in foam. Phys. Rev. E 82, 011405 (2010).

    ADS  MATH  Google Scholar 

  14. Kropka, J. M. & Celina, M. Viscoelasticity of liquid organic foam: relaxations, temporal dependence, and bubble loading effects on flow behavior. J. Chem. Phys. 133, 024904 (2010).

    ADS  Google Scholar 

  15. Gupta, S. et al. Advanced rheological characterization of soft colloidal model systems. J. Phys. Condens. Matter 24, 464102 (2012).

    MATH  Google Scholar 

  16. Basu, A. et al. Rheology of soft colloids across the onset of rigidity: scaling behavior, thermal, and non-thermal responses. Soft Matter 10, 3027–3035 (2014).

    ADS  MATH  Google Scholar 

  17. Hanotin, C., Kiesgen de Richter, S., Michot, L. & Marchal, P. Viscoelasticity of vibrated granular suspensions. J. Rheol. 59, 253–273 (2015).

    ADS  MATH  Google Scholar 

  18. Nishizawa, K. et al. Feedback-tracking microrheology in living cells. Sci. Adv. 3, e1700318 (2017).

    ADS  MATH  Google Scholar 

  19. Nishizawa, K. et al. Universal glass-forming behavior of in vitro and living cytoplasm. Sci. Rep. 7, 15143 (2017).

    ADS  MATH  Google Scholar 

  20. Conley, G. M., Zhang, C., Aebischer, P., Harden, J. L. & Scheffold, F. Relationship between rheology and structure of interpenetrating, deforming and compressing microgels. Nat. Commun. 10, 2436 (2019).

    ADS  Google Scholar 

  21. van Hecke, M. Jamming of soft particles: geometry, mechanics, scaling and isostaticity. J. Phys. Condens. Matter 22, 033101 (2009).

    MATH  Google Scholar 

  22. Liu, A. & Nagel, S. Jamming and Rheology (Taylor & Francis Group, 2020).

  23. O’Hern, C. S., Silbert, L. E., Liu, A. J. & Nagel, S. R. Jamming at zero temperature and zero applied stress: the epitome of disorder. Phys. Rev. E 68, 011306 (2003).

    ADS  MATH  Google Scholar 

  24. Wyart, M. On the rigidity of amorphous solids. Ann. Phys. 30, 1–96 (2005).

    MATH  Google Scholar 

  25. Parisi, G., Urbani, P. & Zamponi, F. Theory of Simple Glasses: Exact Solutions in Infinite Dimensions (Cambridge Univ. Press, 2020).

  26. Katgert, G. & van Hecke, M. Jamming and geometry of two-dimensional foams. Europhys. Lett. 92, 34002 (2010).

    ADS  MATH  Google Scholar 

  27. Lacasse, M.-D., Grest, G. S., Levine, D., Mason, T. & Weitz, D. Model for the elasticity of compressed emulsions. Phys. Rev. Lett. 76, 3448–3451 (1996).

  28. Lemaître, A. & Maloney, C. Sum rules for the quasi-static and visco-elastic response of disordered solids at zero temperature. J. Stat. Phys. 123, 415 (2006).

    ADS  MathSciNet  MATH  Google Scholar 

  29. Tighe, B. P. Relaxations and rheology near jamming. Phys. Rev. Lett. 107, 158303 (2011).

    ADS  MATH  Google Scholar 

  30. Hara, Y., Mizuno, H. & Ikeda, A. Microrheology near jamming. Soft Matter 19, 6046–6056 (2023).

    ADS  Google Scholar 

  31. Phillips, W. Amorphous Solids: Low-temperature Properties (Springer-Verlag, 1981).

  32. Schirmacher, W., Ruocco, G. & Scopigno, T. Acoustic attenuation in glasses and its relation with the boson peak. Phys. Rev. Lett. 98, 025501 (2007).

    ADS  MATH  Google Scholar 

  33. Klinger, M. I. Soft atomic motion modes in glasses: their role in anomalous properties. Phys. Rep. 492, 111–180 (2010).

    ADS  MATH  Google Scholar 

  34. Lin, J., Jorjadze, I., Pontani, L.-L., Wyart, M. & Brujic, J. Evidence for marginal stability in emulsions. Phys. Rev. Lett. 117, 208001 (2016).

    ADS  Google Scholar 

  35. Silbert, L. E., Liu, A. J. & Nagel, S. R. Vibrations and diverging length scales near the unjamming transition. Phys. Rev. Lett. 95, 098301 (2005).

    ADS  Google Scholar 

  36. Silbert, L. E., Liu, A. J. & Nagel, S. R. Normal modes in model jammed systems in three dimensions. Phys. Rev. E 79, 021308 (2009).

    ADS  MATH  Google Scholar 

  37. DeGiuli, E., Laversanne-Finot, A., Düring, G., Lerner, E. & Wyart, M. Effects of coordination and pressure on sound attenuation, boson peak and elasticity in amorphous solids. Soft Matter 10, 5628–5644 (2014).

  38. Charbonneau, P., Corwin, E. I., Parisi, G., Poncet, A. & Zamponi, F. Universal non-Debye scaling in the density of states of amorphous solids. Phys. Rev. Lett. 117, 045503 (2016).

    ADS  MATH  Google Scholar 

  39. Mizuno, H., Shiba, H. & Ikeda, A. Continuum limit of the vibrational properties of amorphous solids. Proc. Natl Acad. Sci. USA 114, E9767–E9774 (2017).

    ADS  MATH  Google Scholar 

  40. Shimada, M., Mizuno, H., Berthier, L. & Ikeda, A. Low-frequency vibrations of jammed packings in large spatial dimensions. Phys. Rev. E 101, 052906 (2020).

    ADS  MATH  Google Scholar 

  41. Franz, S., Parisi, G., Urbani, P. & Zamponi, F. Universal spectrum of normal modes in low-temperature glasses. Proc. Natl Acad. Sci. USA 112, 14539–14544 (2015).

    ADS  MATH  Google Scholar 

  42. Lerner, E., Düring, G. & Bouchbinder, E. Statistics and properties of low-frequency vibrational modes in structural glasses. Phys. Rev. Lett. 117, 035501 (2016).

    ADS  MATH  Google Scholar 

  43. Şenbil, N., Gruber, M., Zhang, C., Fuchs, M. & Scheffold, F. Observation of strongly heterogeneous dynamics at the depinning transition in a colloidal glass. Phys. Rev. Lett. 122, 108002 (2019).

    ADS  Google Scholar 

  44. Schnurr, B., Gittes, F., MacKintosh, F. & Schmidt, C. Determining microscopic viscoelasticity in flexible and semiflexible polymer networks from thermal fluctuations. Macromolecules 30, 7781–7792 (1997).

    ADS  Google Scholar 

  45. Ozawa, M., Berthier, L. & Coslovich, D. Exploring the jamming transition over a wide range of critical densities. SciPost Phys. 3, 027 (2017).

    ADS  Google Scholar 

  46. Brito, C. & Wyart, M. Geometric interpretation of previtrification in hard sphere liquids. J. Chem. Phys. 131, 149 (2009).

    MATH  Google Scholar 

  47. Altieri, A., Franz, S. & Parisi, G. The jamming transition in high dimension: an analytical study of the tap equations and the effective thermodynamic potential. J. Stat. Mech. Theory Exp. 2016, 093301 (2016).

    MathSciNet  MATH  Google Scholar 

  48. Arceri, F. & Corwin, E. I. Vibrational properties of hard and soft spheres are unified at jamming. Phys. Rev. Lett. 124, 238002 (2020).

    ADS  MATH  Google Scholar 

  49. Nishi, K., Kilfoil, M. L., Schmidt, C. F. & MacKintosh, F. A symmetrical method to obtain shear moduli from microrheology. Soft Matter 14, 3716–3723 (2018).

    ADS  Google Scholar 

  50. Uematsu, Y., Chida, K. & Matsubara, H. Intentionally added ionic surfactants induce Jones-Ray effect at air-water interface. Colloid Interface Sci. Commun. 27, 45–48 (2018).

    Google Scholar 

  51. Bitzek, E., Koskinen, P., Gähler, F., Moseler, M. & Gumbsch, P. Structural relaxation made simple. Phys. Rev. Lett. 97, 170201 (2006).

    ADS  Google Scholar 

  52. Shimada, M., Mizuno, H. & Ikeda, A. Anomalous vibrational properties in the continuum limit of glasses. Phys. Rev. E 97, 022609 (2018).

    ADS  MATH  Google Scholar 

Download references

Acknowledgements

We thank H. Mizuno for insightful discussions, and S. Inokuchi, K. Nishi and M. Annaka for their technical support. This work was supported by Hosokawa Powder Technology Foundation grant no. HPTF21509 (Y.H.); JST SPRING grant no. JPMJSP2108 (Y.H.); JST CREST grant no. JPMJCR24T2 (D.M.); JST ERATO grant no. JPMJER2401 (A.I.); and JSPS KAKENHI grant nos. JP20H01868 (A.I.), JP20H00128 (A.I), JP21H01048 (D.M.), JP22H04848 (D.M.), JP22K03552 (H.E.), JP23KJ0368 (Y.H.) and JP24H00192 (A.I.). This work was also supported by the JSPS Core-to-Core Program ‘Advanced core-to-core network for the physics of self-organizing active matter’ (grant no. JPJSCCA20230002; D.M.)

Author information

Authors and Affiliations

  1. Graduate School of Arts and Science, The University of Tokyo, Tokyo, Japan

    Yusuke Hara & Atsushi Ikeda

  2. Department of Physics, Kyushu University, Fukuoka, Japan

    Ryosuke Matsuoka, Hiroyuki Ebata & Daisuke Mizuno

  3. Research Center for Complex Systems Biology, Universal Biology Institute, The University of Tokyo, Tokyo, Japan

    Atsushi Ikeda

Authors
  1. Yusuke Hara
    View author publications

    Search author on:PubMed Google Scholar

  2. Ryosuke Matsuoka
    View author publications

    Search author on:PubMed Google Scholar

  3. Hiroyuki Ebata
    View author publications

    Search author on:PubMed Google Scholar

  4. Daisuke Mizuno
    View author publications

    Search author on:PubMed Google Scholar

  5. Atsushi Ikeda
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Y.H., D.M. and A.I. designed the research. Experimental data were collected by R.M. and D.M. Y.H. carried out the simulations. Y.H., R.M., H.E., D.M. and A.I. analysed the data, discussed the results and wrote the paper.

Corresponding authors

Correspondence to Yusuke Hara, Daisuke Mizuno or Atsushi Ikeda.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Lars Pastewka and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Comparison between macrorheology and microrheology.

a. The macroscopic complex modulus of the soft sphere model calculated by the formula Eq.(32). The packing fraction is set to be ϕ = 0.66. b. The microscopic complex modulus of the soft sphere model calculated by the formula Eq.(19). The packing fraction is set to be ϕ = 0.66. Reproduced from Fig. 3c.

Extended Data Fig. 2 Scaling analysis of the vibrational density of states.

a. P(α−2)/(2α−2)D(ω) is plotted against ω/P1/2 for the soft sphere model, where P is the pressure of the packings. The results for P = 10−5 − 10−2 with N = 8000 are included. According to Eq. (4), the vDOS of the soft sphere model obeys the scaling relation ωeD(ω) = f(ω/ω*) with f(x) ∝ x2 at x < 1. Because the pressure follows the scaling relation \(P\propto {(\phi -{\phi }_{J})}^{\alpha -1}\), we can express the characteristic frequencies as ωe ∝ P(α−2)/(2α−2) and ω* ∝ P1/2. Therefore, the scaling relation can be rewritten as P(α−2)/(2α−2)D(ω) = g(ω/P1/2). The data collapse in the figure confirms this scaling relation of D(ω). b. Same as a but for \(\tilde{D}(\omega )\), the density of eigenfrequencies of \(\propto \tilde{{\bf{{\mathcal{M}}}}}\). The data collapse confirms that D(ω) and \(\tilde{D}(\omega )\) share the same scaling relation.

Extended Data Fig. 3 Scaling analysis of the loss modulus of the soft sphere model.

\({G}^{{\prime\prime} }/\left({\left(\phi -{\phi }_{J}\right)}^{(\alpha -2)/2}{\omega }^{1/2}\right)\) are plotted with respect to \(\omega /{(\phi -{\phi }_{J})}^{(\alpha -2)}\) for our numerical model. This is the same scaling analysis as in Fig. 4a, but for G″ of the numerical model at ϕ = 0.64, 0.65 and 0.66. The result shows that \({G}^{{\prime\prime} }/\left({\left(\phi -{\phi }_{J}\right)}^{(\alpha -2)/2}{\omega }^{1/2}\right)\) approaches to a constant with decreasing the frequency, except for the lowest frequencies. This confirms that our numerical model exhibits \({G}^{{\prime\prime} }\propto \sqrt{\omega }\).

Source data

Source Data Fig. 2

The (x, y) data for Fig. 2a,b.

Source Data Fig. 3

The (x, y) data for Fig. 3a–c.

Source Data Fig. 4

The (x, y) data for Fig. 4a–g.

Source Data Fig. 5

The (x, y) data for Fig. 5a–d.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hara, Y., Matsuoka, R., Ebata, H. et al. A link between anomalous viscous loss and the boson peak in soft jammed solids. Nat. Phys. 21, 262–268 (2025). https://doi.org/10.1038/s41567-024-02722-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02722-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing