Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Direct observation of colloidal quasicrystallization

Nature Physics volume 21, pages 966–973 (2025)Cite this article

Subjects

Abstract

Discovered first in synthetic alloys and subsequently in nature, quasicrystals exhibit forbidden symmetries and long-range orientational order but lack translational periodicity. Despite numerous theoretical and numerical studies, the fabrication of quasicrystals remains a challenge, with limited means available for observing their formation in situ. As a result, questions remain regarding the detailed mechanisms of quasicrystal formation and stabilization. Observable under optical microscopes, micrometre-scale colloidal systems have been used for decades as atomic models with considerably slowed-down dynamics and tuneable interactions through surface modification, solution composition and applied external fields. Here we show that two-dimensional dodecagonal quasicrystals can be reversibly assembled from single-component microspheres using a combination of orthogonally applied magnetic and electric fields. Varying the magnitude and frequency of the applied fields not only determines the resulting structures but also sets the phase transition dynamics via an effective system temperature. We hypothesize that these quasicrystals are energetically stabilized with their formation driven by an isotropic double-well pair potential, although the origin of the second minimum remains an open question.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Formation of QCs.
Fig. 2: Heterogeneous nucleation and growth of QC.
Fig. 3: Homogeneous nucleation and growth of QC.
Fig. 4: Other phase transitions.

Similar content being viewed by others

Data availability

Raw datasets generated during this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.

Code availability

The code of the numerical computations (with detailed documentation) is available on GitHub at https://github.com/stochasticHydroTools/RigidMultiblobsWall/tree/master/Lubrication/Lubrication_Examples/Colloidal_QuasiCrystal.

References

  1. Shechtman, D., Blech, I., Gratias, D. & Cahn, J. W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951–1953 (1984).

    Article  ADS  Google Scholar 

  2. Bindi, L., Steinhardt, P. J., Yao, N. & Lu, P. J. Natural quasicrystals. Science 324, 1306–1309 (2009).

    Article  ADS  Google Scholar 

  3. Levi, L. et al. Disorder-enhanced transport in photonic quasicrystals. Science 332, 1541–1544 (2011).

    Article  ADS  Google Scholar 

  4. Matsui, T., Agrawal, A., Nahata, A. & Vardeny, Z. V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 446, 517–521 (2007).

    Article  ADS  Google Scholar 

  5. Vardeny, Z. V., Nahata, A. & Agrawal, A. Optics of photonic quasicrystals. Nat. Photonics 7, 177–187 (2013).

    Article  ADS  Google Scholar 

  6. Yu, S., Qiu, C.-W., Chong, Y., Torquato, S. & Park, N. Engineered disorder in photonics. Nat. Rev. Mater. 6, 226–243 (2021).

    Article  ADS  Google Scholar 

  7. PaBens, M. et al. Interface-driven formation of a two-dimensional dodecagonal fullerene quasicrystal. Nat. Commun. 8, 15367 (2017).

    Article  ADS  Google Scholar 

  8. Wasio, N. A. et al. Self-assembly of hydrogen-bonded two-dimensional quasicrystals. Nature 507, 86–89 (2014).

    Article  ADS  Google Scholar 

  9. Urgel, J. I. et al. Quasicrystallinity expressed in two-dimensional coordination networks. Nat. Chem. 8, 657–662 (2016).

    Article  Google Scholar 

  10. Talapin, D. V. et al. Quasicrystalline order in self-assembled binary nanoparticle superlattices. Nature 461, 964–967 (2009).

    Article  ADS  Google Scholar 

  11. Xiao, C., Fujita, N., Miyasaka, K., Sakamoto, Y. & Terasaki, O. Dodecagonal tiling in mesoporous silica. Nature 487, 349–353 (2012).

    Article  ADS  Google Scholar 

  12. Ye, X. et al. Quasicrystalline nanocrystal superlattice with partial matching rules. Nat. Mater. 16, 214–219 (2017).

    Article  ADS  Google Scholar 

  13. Nagaoka, Y., Zhu, H., Eggert, D. & Chen, O. Single-component quasicrystalline nanocrystal superlattices through flexible polygon tiling rule. Science 362, 1396–1400 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  14. Fischer, S. et al. Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry. Proc. Natl Acad. Sci. USA 108, 1810–1814 (2011).

    Article  ADS  Google Scholar 

  15. Yue, K. et al. Geometry induced sequence of nanoscale Frank–Kasper and quasicrystal mesophases in giant surfactants. Proc. Natl Acad. Sci. USA 113, 14195–14200 (2016).

    Article  ADS  Google Scholar 

  16. Liu, L., Li, Z., Li, Y. & Mao, C. Rational design and self-assembly of two-dimensional, dodecagonal DNA quasicrystals. J. Am. Chem. Soc. 141, 4248–4251 (2019).

    Article  Google Scholar 

  17. Zhang, J. & Bates, F. S. Dodecagonal quasicrystalline morphology in a poly(styrene-b-isoprene-b-styrene-b-ethylene oxide) tetrablock terpolymer. J. Am. Chem. Soc. 134, 7636–7639 (2012).

    Article  Google Scholar 

  18. Hayashida, K., Dotera, T., Takano, A. & Matsushita, Y. Polymeric quasicrystal: mesoscopic quasicrystalline tiling in ABC star polymers. Phys. Rev. Lett. 98, 195502 (2007).

    Article  ADS  Google Scholar 

  19. Gillard, T. M., Lee, S. & Bates, F. S. Dodecagonal quasicrystalline order in a diblock copolymer melt. Proc. Natl Acad. Sci. USA 113, 5167–5172 (2016).

    Article  ADS  Google Scholar 

  20. Steurer, W. Quasicrystals: What do we know? What do we want to know? What can we know? Acta Crystallogr. Sect. A 74, 1–11 (2018).

    Article  MathSciNet  Google Scholar 

  21. Nagaoka, Y., Schneider, J., Zhu, H. & Chen, O. Quasicrystalline materials from non-atom building blocks. Matter 6, 30–58 (2023).

    Article  Google Scholar 

  22. Du, D., Li, D., Thakur, M. & Biswal, S. L. Generating an in situ tunable interaction potential for probing 2-D colloidal phase behavior. Soft Matter 9, 6867–6875 (2013).

    Article  ADS  Google Scholar 

  23. Haji-Akbari, A. et al. Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra. Nature 462, 773–777 (2009).

    Article  ADS  Google Scholar 

  24. Dotera, T., Oshiro, T. & Ziherl, P. Mosaic two-lengthscale quasicrystals. Nature 506, 208–211 (2014).

    Article  ADS  Google Scholar 

  25. van der Linden, M. N., Doye, J. P. K. & Louis, A. A. Formation of dodecagonal quasicrystals in two-dimensional systems of patchy particles. J. Chem. Phys. 136, 054904 (2012).

    Article  ADS  Google Scholar 

  26. Barkan, K., Engel, M. & Lifshitz, R. Controlled self-assembly of periodic and aperiodic cluster crystals. Phys. Rev. Lett. 113, 098304 (2014).

    Article  ADS  Google Scholar 

  27. Iacovella, C. R., Keys, A. S. & Glotzer, S. C. Self-assembly of soft-matter quasicrystals and their approximants. Proc. Natl Acad. Sci. USA 108, 20935–20940 (2011).

    Article  ADS  Google Scholar 

  28. Fayen, E., Filion, L., Foffi, G. & Smallenburg, F. Quasicrystal of binary hard spheres on a plane stabilized by configurational entropy. Phys. Rev. Lett. 132, 048202 (2024).

    Article  ADS  Google Scholar 

  29. Scacchi, A., Somerville, W. R. C., Buzza, D. M. A. & Archer, A. J. Quasicrystal formation in binary soft matter mixtures. Phys. Rev. Res. 2, 032043 (2020).

    Article  Google Scholar 

  30. Pattabhiraman, H. & Dijkstra, M. On the formation of stripe, sigma, and honeycomb phases in a core–corona system. Soft Matter 13, 4418–4432 (2017).

    Article  ADS  Google Scholar 

  31. Skibinsky, A., Buldyrev, S. V., Scala, A., Havlin, S. & Stanley, H. E. Quasicrystals in a monodisperse system. Phys. Rev. E 60, 2664–2669 (1999).

    Article  ADS  Google Scholar 

  32. Zu, M., Tan, P. & Xu, N. Forming quasicrystals by monodisperse soft core particles. Nat. Commun. 8, 2089 (2017).

    Article  ADS  Google Scholar 

  33. Schoberth, H. G. et al. Molecular dynamics study of colloidal quasicrystals. Soft Matter 12, 7644–7654 (2016).

    Article  ADS  Google Scholar 

  34. Pattabhiraman, H., Gantapara, A. P. & Dijkstra, M. On the stability of a quasicrystal and its crystalline approximant in a system of hard disks with a soft corona. J. Chem. Phys. 143, 164905 (2015).

    Article  ADS  Google Scholar 

  35. Lu, P. J. & Weitz, D. A. Colloidal particles: crystals, glasses, and gels. Annu. Rev. Condens. Matter Phys. 4, 217–233 (2013).

    Article  ADS  Google Scholar 

  36. Manoharan, V. N. Colloids. Colloidal matter: packing, geometry, and entropy. Science 349, 1253751 (2015).

    Article  Google Scholar 

  37. Li, B., Zhou, D. & Han, Y. Assembly and phase transitions of colloidal crystals. Nat. Rev. Mater. 1, 15011 (2016).

    Article  ADS  Google Scholar 

  38. Ceron, S., Gardi, G., Petersen, K. & Sitti, M. Programmable self-organization of heterogeneous microrobot collectives. Proc. Natl Acad. Sci. USA 120, e2221913120 (2023).

    Article  Google Scholar 

  39. Hermisson, J., Richard, C. & Baake, M. A guide to the symmetry structure of quasiperiodic tiling classes. J. Phys. I 7, 1003–1018 (1997).

    MathSciNet  Google Scholar 

  40. Leung, P. W., Henley, C. L. & Chester, G. V. Dodecagonal order in a two-dimensional lennard-jones system. Phys. Rev. B 39, 446–458 (1989).

    Article  ADS  MathSciNet  Google Scholar 

  41. Rubinstein, B. & Ben-Abraham, S. I. Vertex frequencies of the hierarchical dodecagonal tiling. Ferroelectrics 250, 417–419 (2001).

    Article  ADS  Google Scholar 

  42. Lieu, U. T. & Yoshinaga, N. Formation and fluctuation of two-dimensional dodecagonal quasicrystals. Soft Matter 18, 7497–7509 (2022).

    Article  ADS  Google Scholar 

  43. Shirzad, K. & Viney, C. A critical review on applications of the avrami equation beyond materials science. J. R. Soc. Interface 20, 20230242 (2023).

    Article  Google Scholar 

  44. Hensley, A., Videbæk, T. E., Seyforth, H., Jacobs, W. M. & Rogers, W. B. Macroscopic photonic single crystals via seeded growth of DNA-coated colloids. Nat. Commun. 14, 4237 (2023).

    Article  ADS  Google Scholar 

  45. Dotera, T. Toward the discovery of new soft quasicrystals: from a numerical study viewpoint. J. Polym. Sci. Part B 50, 155–167 (2012).

    Article  Google Scholar 

  46. Ristenpart, W. D., Aksay, I. A. & Saville, D. A. Electrohydrodynamic flow around a colloidal particle near an electrode with an oscillating potential. J. Fluid Mech. 575, 83–109 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  47. Fernández-Mateo, R., García-Sánchez, P., Calero, V., Morgan, H. & Ramos, A. Stationary electro-osmotic flow driven by AC fields around charged dielectric spheres. J. Fluid Mech. 924, R2 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  48. Grob, D. T., Wise, N., Oduwole, O. & Sheard, S. Magnetic susceptibility characterization of superparamagnetic microspheres. J. Magn. Magn. Mater. 452, 134–140 (2018).

    Article  ADS  Google Scholar 

  49. Zimmermann, C., Herson, P., Neeves, K. & Marr, D. Multimodal microwheel swarms for targeting in three-dimensional networks. Sci. Rep. 12, 5078 (2022).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge discussions with D. T. Wu on QCs and J. R. Maestas on phason strain calculations. Y.G., D.W.M.M. and N.W. acknowledge support from the National Science Foundation (CBET-1762616) and the National Aeronautics and Space Administration (NNX13AQ54G). N.W. also acknowledges support from the National Science Foundation (CBET-2030480).

Author information

Authors and Affiliations

  1. Materials Science and Engineering Program, Colorado School of Mines, Golden, CO, USA

    Yan Gao

  2. Department of Applied Mathematics and Statistics, Colorado School of Mines, Golden, CO, USA

    Brennan Sprinkle

  3. Department of Chemical and Biological Engineering, Colorado School of Mines, Golden, CO, USA

    David W. M. Marr & Ning Wu

Authors
  1. Yan Gao
    View author publications

    Search author on:PubMed Google Scholar

  2. Brennan Sprinkle
    View author publications

    Search author on:PubMed Google Scholar

  3. David W. M. Marr
    View author publications

    Search author on:PubMed Google Scholar

  4. Ning Wu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

N.W. and D.W.M.M. conceived and designed the work. Y.G. performed the experiments. B.S. performed the simulation work. All authors contributed to the data analysis and the writing of the paper.

Corresponding authors

Correspondence to David W. M. Marr or Ning Wu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Martin Dulle and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

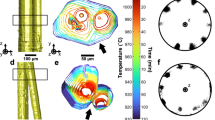
Extended Data Fig. 1 Experimental setup and magnetic field configuration.

a, The application of orthogonal magnetic and electric fields. b, In-situ measurement of the diffraction pattern. c, The planar oscillating magnetic field (\({\boldsymbol{B}}={B}_{0}\cos \left(2\pi {f}_{B}t\right)\hat{{\bf{x}}}+{B}_{0}\sin \left(4\pi {f}_{B}t\right)\hat{{\bf{y}}}\)) can generate time-averaged attractive magnetic interactions between particles while minimizing net particle rotation. The colored arrows indicate the instantaneous field orientation and magnitude over one period, T = 1/fB.

Extended Data Fig. 2 Ideal QC constructed using the extended Schlottmann inflation rule.

a, The real-space structure and local particle environments. The Z, σ, and H environments are labeled in green, red, and yellow, respectively. The particles at the boundaries are labeled in yellow. b, The corresponding diffraction pattern.

Source data

Extended Data Fig. 3 Large field of view of Fig. 1c.

a, Large field of view of Fig. 1c (~8663 particles). b, The local particle environments following the color codes specified in Fig. 1d.

Source data

Extended Data Fig. 4 Heterogeneous HX-to-QC transition initiated from a domain boundary.

The real-space optical image is overlayed with the particle environment identification following the same color codes specified in Fig. 1d (E0 = 1.14 × 105 V/m, B0 = 0.92 mT, and fB = 80 Hz). The phase transition is triggered by increasing fE from 1k to 20k Hz.

Source data

Extended Data Fig. 5 The local bond orientation order of a poly-quasicrystalline structure shown in Fig. 4d.

a, Magnitude. b, Phase.

Source data

Extended Data Fig. 6 The assembly of 2.8 µm particles (M-270 carboxylic acid) under electric and magnetic fields.

a, Closed-packed ladder formed under a magnetic field only (B0 = 1.32 mT, and fB = 80 Hz) is transformed into a mixture of equilateral triangles and squares under combined electric and magnetic fields (E0 = 1.2 × 105 V/m, fE = 2k Hz, B0 = 1.32 mT, and fB = 80 Hz). b, QC formation at higher particle concentration (E0 = 1.14 × 105 V/m, B0 = 1.32 mT, and fB = 80 Hz). The real space image is overlayed with the local particle environments. c, Calculated diffraction pattern. d, Phase diagram (B0 = 1.53 mT, fB = 80 Hz). 0.033 wt% F127 is added to the suspension.

Source data

Extended Data Fig. 7 Permanent dipole moment measurement.

a, The angular frequency of a spinning bead under a circularly rotating magnetic field at different field strengths and frequencies. Error bars are standard deviation (SD) for n = 10 independent measurements. Data are presented as mean values +/− SD. b, The dependence of cutoff frequency on field strength. Error bars are standard deviation for n = 10 independent measurements. Data are presented as mean values +/− SD. c, The orientation of a polystyrene nanoparticle (NP) labeled bead under an applied DC magnetic field (B = 0.5 mT). The black arrow indicates the direction of the magnetic field. The white arrow represents the particle orientation defined by the vector connecting the particle center to the NP centroid. d-e, When the applied field is suddenly rotated 150° counterclockwise, the particle also rotates 150° as indicated by its orientation vector.

Source data

Extended Data Fig. 8 The susceptibility χ and electric polarization coefficient K of M-450 epoxy particles.

a, The separation between particle pairs under a one-dimensional DC magnetic field (B0 = 1.0 mT). Each color represents results obtained from a single pair of particles. b, The separation between particle pairs under a vertical AC electric field (E0 = 105 V/m and fE = 9 kHz). Dashed lines represent the lower and upper bounds of the fit.

Source data

Extended Data Fig. 9 Non close-packed hexagonal arrays formed under an AC electric field only.

a-e, The frequency changes from 0.6k to 20k Hz while E0 is kept constant (105 V/m). The scale bar (20 µm) is the same for all figures. f, The separation between neighboring particles at different frequencies. Error bars represent mean ± SD (n = 200 independent measurements).

Source data

Extended Data Fig. 10 Assembly of M-270 carboxylic acid particles in DMSO.

a, Close-packed clusters under an in-plane oscillating magnetic field. B0 = 2.1 mT and fB = 80 Hz. b, The same clusters upon the superposition of an out-of-plane electric field (E0 = 1.2 × 105 V/m, fE = 600 Hz).

Supplementary information

Supplementary Information

Supplementary Sections 1–5, Table 1 and video descriptions.

Supplementary Video 1

The transformation of small colloidal clusters under orthogonal electric and magnetic fields. Under a planar rotating magnetic field (B0 = 0.92 mT, fB,x = fB,y = 80 Hz), four (ten) particles form a diamond-like (ladder-like) cluster. After this, the magnetic field is switched to an oscillating magnetic field, where \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, stopping rotation. After superimposing a vertical electric field (E0 = 1.3 × 105 V m−1, fE = 1,000 Hz), the cluster transforms into a square (mixed triangle–square).

Supplementary Video 2

HX-to-QC phase transition: heterogeneous nucleation from one side of the domain boundary. The real-space images, particle environment, calculated diffraction patterns, \({\psi }_{12}\) and \({\theta }_{12}\) are shown. Electric field frequency fE is increased from 1,000 to 20,000 Hz while other field conditions are kept constant (B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.14 × 105 V m−1). The grain boundary (not shown) is located at right. In real-space images of the QC phase, not all bright circles correspond to the centre of the particles. Those located at the centre of squares are voids. All videos are sped up 5×.

Supplementary Video 3

θ12 histogram during the HX-to-QC transition.

Supplementary Video 4

HX-to-QC phase transition: heterogeneous nucleation from both sides of the domain boundary. The real-space images, particle environment, calculated diffraction patterns, ψ12 and θ12 are shown. The electric field frequency fE is increased from 1,000 to 20,000 Hz while other field conditions are kept constant (B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.14 × 105 V m−1). All videos are sped up 1.5×.

Supplementary Audio 5

HX-to-QC phase transition: homogeneous nucleation from the bulk of a hexagonal crystal. The real-space images, particle environment, calculated diffraction patterns, ψ12 and θ12 are shown. The electric field frequency fE is increased from 1,000 to 20,000 Hz while other field conditions are kept constant (B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.2 × 105 V m−1). All videos are sped up 3×.

Supplementary Video 6

HX-to-QC phase transition: homogeneous nucleation from the bulk of a hexagonal crystal. Part I: the HX transforms into QC when the electric field frequency fE is increased from 1,000 to 20,000 Hz directly while other field conditions (B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.2 × 105 V m−1) are held constant. Part II: the HX transforms into QC when the electric field frequency fE is increased from 1,000 to 10,000 Hz and then to 20,000 Hz via a two-step change. Other field conditions (B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.2 × 105 V m−1) are held constant. Both videos are sped up 3×.

Supplementary Video 7

SQ-to-σ and SQ-to-H phase transitions. Part I: phase transition from a square lattice to a σ phase. The magnetic field is increased from B0 = 0.92 to 1.00 mT. \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, E0 = 1.2 × 105 V m−1, fE = 3,000 Hz. Part II: phase transition from a square lattice to an H phase. Bx is increased from 0.92 to 1.07 mT while other field conditions are kept constant. \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz, By = 0.92 mT, E0 = 1.2 × 105 V m−1, fE = 3,000 Hz.

Supplementary Video 8

Liquid-to-QC phase transition. Particles are suspended in a thin liquid film confined between two ITO glasses separated by 50 μm. The surface density is ~60%. When the applied electric field and magnetic field (E0 = 1.15 × 105 V m−1, fE = 3,000 Hz, B0 = 0.92 mT, \({f}_{B,y}=2{f}_{B,x}\) = 160 Hz) are applied simultaneously, particles aggregate and form QCs. Both videos are sped up 3×.

Supplementary Video 9

Reorientation of an isolated particle under a d.c. magnetic field. The microparticle is first coated with a 500-nm fluorescent polystyrene nanoparticle to identify the orientation (B0 = 0.5 mT). The video is sped up 3×.

Supplementary Video 10

Experiment and numerical simulation of particles with permanent magnetic dipoles under orthogonally applied magnetic and electric fields. Part I: a ladder-like hexamer is transformed into triangle–square packing and then a ring as the electric field increases. Left: experiment. Right: simulation. The arrows show the orientation of the permanent dipoles. Part II: transformation from hexagonal colloidal clusters to σ and H motifs upon the application of electric field. Left: experiment. Right: simulation. Other field conditions are constant (B0 = 0.92 mT, fB = 80 Hz, fE = 9,000 Hz). The video is sped up 3×.

Source data

Source Data Fig. 1

Source data for Fig. 1.

Source Data Fig. 2

Source data for Fig. 2.

Source Data Fig. 3

Source data for Fig. 3.

Source Data Fig. 4

Source data for Fig. 4.

Source Data Extended Data Fig. 2

Source data for Extended Data Fig. 2.

Source Data Extended Data Fig. 3

Source data for Extended Data Fig. 3.

Source Data Extended Data Fig. 4

Source data for Extended Data Fig. 4.

Source Data Extended Data Fig. 5

Source data for Extended Data Fig. 5.

Source Data Extended Data Fig. 6

Source data for Extended Data Fig. 6.

Source Data Extended Data Fig. 7

Source data for Extended Data Fig. 7.

Source Data Extended Data Fig. 8

Source data for Extended Data Fig. 8.

Source Data Extended Data Fig. 9

Source data for Extended Data Fig. 9.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, Y., Sprinkle, B., Marr, D.W.M. et al. Direct observation of colloidal quasicrystallization. Nat. Phys. 21, 966–973 (2025). https://doi.org/10.1038/s41567-025-02859-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02859-z

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing