Abstract
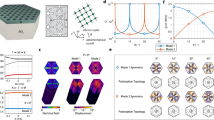
Increasing the number of particles in a system often leads to qualitative changes in its properties, such as breaking of symmetries and the appearance of phase transitions. This renders a macroscopic system fundamentally different from its individual microscopic constituents. Lying between these extremes, mesoscopic systems exhibit microscopic fluctuations that influence behaviour on longer length scales, leading to critical phenomena and dynamics. Therefore, tracing the properties of well-controlled mesoscopic systems can help bridge the gap between an exact description of few-body microscopic systems and the emergent description of many-body systems. Here we explore the mesoscopic signatures of an optomechanical self-organization phase transition using arrays of cold atoms inside an optical cavity. By precisely engineering atom–cavity interactions, we reveal how critical behaviour depends on the atom number, identify characteristic dynamical behaviours in the self-organized regime and observe a finite optomechanical susceptibility at the critical point. These findings advance our understanding of particle-number- and time-resolved properties of phase transitions in mesoscopic systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Code availability
Code is available from the corresponding author upon reasonable request.
References
Anderson, P. More is different. Science 177, 393–396 (1972).
Jou, D. & Restuccia, L. Mesoscopic transport equations and contemporary thermodynamics: an introduction. Contemp. Phys. 52, 465–474 (2011).
Iachello, F. & Zamfir, N. V. Quantum phase transitions in mesoscopic systems. Phys. Rev. Lett. 92, 212501 (2004).
Vidal, J. & Dusuel, S. Finite-size scaling exponents in the Dicke model. Europhys. Lett. 74, 817–822 (2006).
Stitely, K. C., Masson, S. J., Giraldo, A., Krauskopf, B. & Parkins, S. Superradiant switching, quantum hysteresis, and oscillations in a generalized Dicke model. Phys. Rev. A 102, 063702 (2020).
Karapetrov, G., Fedor, J., Iavarone, M., Rosenmann, D. & Kwok, W. K. Direct observation of geometrical phase transitions in mesoscopic superconductors by scanning tunneling microscopy. Phys. Rev. Lett. 95, 167002 (2005).
Bird, J. et al. Quantum transport in open mesoscopic cavities. Chaos Solitons Fractals 8, 1299–1324 (1997).
Knoll, A. et al. Direct imaging and mesoscale modelling of phase transitions in a nanostructured fluid. Nat. Mater. 3, 886–891 (2004).
Matheny, M. H. et al. Exotic states in a simple network of nanoelectromechanical oscillators. Science 363, eaav7932 (2019).
Wollack, E. A. et al. Quantum state preparation and tomography of entangled mechanical resonators. Nature 604, 463–467 (2022).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Ren, H. et al. Topological phonon transport in an optomechanical system. Nat. Commun. 13, 3476 (2022).
Andrade, L. H. F. et al. Damped precession of the magnetization vector of superparamagnetic nanoparticles excited by femtosecond optical pulses. Phys. Rev. Lett. 97, 127401 (2006).
Thirion, C., Wernsdorfer, W. & Mailly, D. Switching of magnetization by nonlinear resonance studied in single nanoparticles. Nat. Mater. 2, 524–527 (2003).
Bayha, L. et al. Observing the emergence of a quantum phase transition shell by shell. Nature 587, 583–587 (2020).
Brantut, J.-P., Meineke, J., Stadler, D., Krinner, S. & Esslinger, T. Conduction of ultracold fermions through a mesoscopic channel. Science 337, 1069–1071 (2012).
Zeiher, J., Wolf, J., Isaacs, J. A., Kohler, J. & Stamper-Kurn, D. M. Tracking evaporative cooling of a mesoscopic atomic quantum gas in real time. Phys. Rev. X 11, 041017 (2021).
Gorman, D. J. et al. Engineering vibrationally assisted energy transfer in a trapped-ion quantum simulator. Phys. Rev. X 8, 011038 (2018).
Guo, Y. et al. Observation of the 2D–1D crossover in strongly interacting ultracold bosons. Nat. Phys. 20, 934–938 (2024).
Safavi-Naini, A. et al. Verification of a many-ion simulator of the Dicke model through slow quenches across a phase transition. Phys. Rev. Lett. 121, 040503 (2018).
Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794–800 (2016).
Kaufman, A. M. & Ni, K.-K. Quantum science with optical tweezer arrays of ultracold atoms and molecules. Nat. Phys. 17, 1324–1333 (2021).
Browaeys, A. & Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 16, 132–142 (2020).
Ritsch, H., Domokos, P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 85, 553–601 (2013).
Mivehvar, F., Piazza, F., Donner, T. & Ritsch, H. Cavity QED with quantum gases: new paradigms in many-body physics. Adv. Phys. 70, 1–153 (2021).
Kirton, P., Roses, M. M., Keeling, J. & Dalla Torre, E. G. Introduction to the Dicke model: from equilibrium to nonequilibrium, and vice versa. Adv. Quantum Technol. 2, 1800043 (2019).
Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010).
Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87–90 (2017).
Morales, A., Zupancic, P., Léonard, J., Esslinger, T. & Donner, T. Coupling two order parameters in a quantum gas. Nat. Mater. 17, 686–690 (2018).
Kongkhambut, P. et al. Observation of a continuous time crystal. Science 377, 670–673 (2022).
Zhiqiang, Z. et al. Nonequilibrium phase transition in a spin-1 Dicke model. Optica 4, 424–429 (2017).
Black, A. T., Chan, H. W. & Vuletić, V. Observation of collective friction forces due to spatial self-organization of atoms: from Rayleigh to Bragg scattering. Phys. Rev. Lett. 91, 203001 (2003).
Deist, E. et al. Mid-circuit cavity measurement in a neutral atom array. Phys. Rev. Lett. 129, 203602 (2022).
Deist, E., Gerber, J. A., Lu, Y.-H., Zeiher, J. & Stamper-Kurn, D. M. Superresolution microscopy of optical fields using tweezer-trapped single atoms. Phys. Rev. Lett. 128, 083201 (2022).
Kimble, H. J. Strong interactions of single atoms and photons in cavity QED. Phys. Scr. 1998, 127 (1998).
Yan, Z. et al. Superradiant and subradiant cavity scattering by atom arrays. Phys. Rev. Lett. 131, 253603 (2023).
Reimann, R. et al. Cavity-modified collective Rayleigh scattering of two atoms. Phys. Rev. Lett. 114, 023601 (2015).
Begley, S., Vogt, M., Gulati, G. K., Takahashi, H. & Keller, M. Optimized multi-ion cavity coupling. Phys. Rev. Lett. 116, 223001 (2016).
Neuzner, A., Körber, M., Morin, O., Ritter, S. & Rempe, G. Interference and dynamics of light from a distance-controlled atom pair in an optical cavity. Nat. Photon. 10, 303–306 (2016).
Schütz, S., Jäger, S. B. & Morigi, G. Thermodynamics and dynamics of atomic self-organization in an optical cavity. Phys. Rev. A 92, 063808 (2015).
Arnold, K. J., Baden, M. P. & Barrett, M. D. Self-organization threshold scaling for thermal atoms coupled to a cavity. Phys. Rev. Lett. 109, 153002 (2012).
Niedenzu, W., Grießer, T. & Ritsch, H. Kinetic theory of cavity cooling and self-organisation of a cold gas. Europhys. Lett. 96, 43001 (2011).
Landau, L. in On the Theory of Phase Transitions 193–216 (Elsevier, 1965).
Zhang, X. et al. Observation of a superradiant quantum phase transition in an intracavity degenerate Fermi gas. Science 373, 1359–1362 (2021).
Néel, L. Thermoremanent magnetization of fine powders. Rev. Mod. Phys. 25, 293–295 (1953).
Knobel, M. et al. Superparamagnetism and other magnetic features in granular materials: a review on ideal and real systems. J. Nanosci. Nanotechnol. 8, 2836–2857 (2008).
Mottl, R. et al. Roton-type mode softening in a quantum gas with cavity-mediated long-range interactions. Science 336, 1570–1573 (2012).
Helson, V. et al. Density-wave ordering in a unitary Fermi gas with photon-mediated interactions. Nature 618, 716–720 (2023).
Vukics, A., Dombi, A., Fink, J. M. & Domokos, P. Finite-size scaling of the photon-blockade breakdown dissipative quantum phase transition. Quantum 3, 150 (2019).
Di Terlizzi, I. et al. Variance sum rule for entropy production. Science 383, 971–976 (2024).
Su, L. et al. Fast single atom imaging for optical lattice arrays. Nat. Commun. 16, 1017 (2025).
Luo, C. et al. Momentum-exchange interactions in a Bragg atom interferometer suppress Doppler dephasing. Science 384, 551–556 (2024).
Periwal, A. et al. Programmable interactions and emergent geometry in an array of atom clouds. Nature 600, 630–635 (2021).
Kroeze, R. M. et al. Directly observing replica symmetry breaking in a vector quantum-optical spin glass. Preprint at https://doi.org/10.48550/arXiv.2311.04216 (2024).
Ye, M. et al. Universal quantum optimization with cold atoms in an optical cavity. Phys. Rev. Lett. 131, 103601 (2023).
Torggler, V., Aumann, P., Ritsch, H. & Lechner, W. A quantum N-queens solver. Quantum 3, 149 (2019).
Anikeeva, G. et al. Number partitioning with Grover’s algorithm in central spin systems. PRX Quantum 2, 020319 (2021).
Ilias, T., Yang, D., Huelga, S. F. & Plenio, M. B. Criticality-enhanced quantum sensing via continuous measurement. PRX Quantum 3, 010354 (2022).
Fernández-Lorenzo, S. & Porras, D. Quantum sensing close to a dissipative phase transition: symmetry breaking and criticality as metrological resources. Phys. Rev. A 96, 013817 (2017).
Tsang, M. Quantum transition-edge detectors. Phys. Rev. A 88, 021801 (2013).
Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 354, 1024–1027 (2016).
Acknowledgements
We thank N. Song for assistance in the laboratory. We acknowledge support from the AFOSR (grant no. FA9550-1910328 (D.M.S.-K.)) and Young Investigator Prize grant no. 21RT0751 (A.A.-G.), from ARO through the MURI program (grant no. W911NF-20-1-0136 (D.M.S.-K.)), from DARPA (grant no. W911NF2010090 (D.M.S.-K.)), from the NSF (QLCI program through grant no. OMA-2016245 (D.M.S.-K.) and CAREER award no. 2047380 (A.A.-G.)), from the David and Lucile Packard Foundation (A.A.-G.), and from the US Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Systems Accelerator (D.M.S.-K.). J.H. acknowledges support from the Department of Defense through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program. C.C.R. acknowledges support from the European Union’s Horizon Europe programme under the Marie-Skłodowska Curie Action LIME (grant no. 101105916).
Author information
Authors and Affiliations
Contributions
J.H., Y.-H.L., Z.Y. and T.X. contributed to building the experimental setup, performing the experiments and analysing the data. C.C.R., S.J.M., A.A.-G., D.M.S.-K. and J.H. contributed to the theoretical model. Z.Y. and D.M.S.-K. conceived the experiments. All authors contributed to the writing of the manuscript and discussed the results. All work was supervised by D.M.S.-K. and A.A.-G.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Peter Domokos and Jean-Philippe Brantut for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Schematic of the heterodyne detection system.
The pump and LO beams originate from separate fibres and are combined at a polarizing beamsplitter (PBS) with orthogonal polarizations. They are then both sent into a single-mode fibre, which ensures that they are mode-matched at the fibre output. Upon emerging from the fibre, they pass through a half-waveplate (labeled as λ/2) at 45∘ and are split at another PBS. Each output port of the last PBS is directed to a sensor on a balanced photodetector, which subtracts the signals on the two sensors. The output voltage of the detector is proportional to \({E}_{{\rm{LO}}}{E}_{{\rm{cav}}}\sin (\varDelta \omega t+\vartheta +\phi )\) where ELO is the LO electric field amplitude, Ecav is the cavity electric field amplitude, Δω = 2π × 20 MHz is the frequency difference between the pump and LO, ϕ is the phase of the LO relative to the pump, and ϑ is the phase of the cavity field relative to the pump.
Extended Data Fig. 2 Example time traces of the detected field in each of the three pumping frames.
a, Scatter plots of the complex cavity field before phase correction. The real (Re(\(\langle \hat{c}_\vartheta \rangle\))) and imaginary (Im(\(\langle \hat{c}_\vartheta \rangle\))) quadratures of the detected field with respect to the average phase of the cavity emission, ϑ, are plotted. Lighter points indicate earlier times and darker points indicate later times. From these data, the angle ϕ of the major axis in each frame is determined by PCA. b, Detected field after rotation by ϕ. Because PCA only determines the angle of the major axis up to a π rotation, in the antinode frames, we define the average projection of the field onto the axis defined by ϑ to be positive. The sign of the node frame is determined by comparing ϑnode to the angle linearly interpolated from ϑfirst frame and ϑlast frame and assuming that the two angles are within π/2 of each other. c, Time traces of cproj. Values of cproj are obtained by projecting the phase-corrected measurements of \(\hat{c}\) (shown in (b)) onto the ϑ-axis. The shaded dark purple regions indicate the shot noise level. Data shown in figure were taken with N = 18, Δpa = − 2π × 80 MHz, Δpc = − 2π × 2.15 MHz, and Ω = 2π × 63.9 MHz.
Extended Data Fig. 3 Dependence of the critical point on Δpa.
a, Data showing the bifurcation for 20 atoms at four values of Δpa. Markers represent the maxima of the fitted Boltzmann probability distribution of cproj. Shaded areas show the width of the distribution at half-maximum. Different pump-cavity detunings were chosen for each setting of Δpa to compensate for the different dispersive shifts on the cavity resonance frequency for 20 atoms placed at the nodes. The values used are Δpc = − 2π × {1.79, 1.9, 2.02, 2.26} MHz corresponding to Δpa = − 2π × {100, 80, 60, 40} MHz. These correspond approximately to Δpc(T) ≃ − 2π × 1.6 MHz when accounting for the shift that thermal atoms put on the cavity resonance frequency. b, Extracted Ωc (circles) exhibit an approximately linear dependence on Δpa. The dashed line shows a fit to equation (4), which gives a fitted temperature of T = 66 ± 8 μK. The shaded region shows the prediction of equation (4) for the independent temperature measurement. Error bars are smaller than the markers.
Extended Data Fig. 4 Interpolation of Ωc from Boltzmann fits.
a, Data showing the bifurcation for 20 atoms at Δpa = 2π × 80 MHz. Markers represent the maxima of the fitted Boltzmann probability distribution of cproj. Blue shaded areas show the width of the distribution at half-maximum. Bottom insets show histograms (light blue) and Boltzmann fits (dark blue) for values of Ω in the gray shaded region. b, By fitting experimentally obtained distributions, such as those shown in (a), to the Boltzmann distribution, we extract the parameter B at different values of Ω for various N. The N shown here correspond to the data shown in Fig. 2a of the main text. The value of Ωc (stars) is linearly interpolated from the two points directly on either side of the B = 0 line. Error bars on the fitted B values are smaller than the markers. Lines are guides to the eye.
Supplementary information
Supplementary Information
Supplementary Sections I–IV, Equations (1)–(34) and Fig. 1.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ho, J., Lu, YH., Xiang, T. et al. Optomechanical self-organization in a mesoscopic atom array. Nat. Phys. 21, 1071–1077 (2025). https://doi.org/10.1038/s41567-025-02916-7
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02916-7
This article is cited by
-
Atoms revolt against tweezer-imposed order
Nature Physics (2025)