Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Supersolid-like sound modes in a driven quantum gas

Nature Physics volume 21, pages 1064–1070 (2025)Cite this article

Subjects

Abstract

Driven systems are of fundamental scientific interest, as they can exhibit properties distinct from the same system at equilibrium. In certain cases, long-lived states of driven matter can emerge with new material properties. Here we probe the excitation spectrum of an emergent patterned state in a driven superfluid and find that its response is identical to that of a one-dimensional supersolid. By preparing wave packets as well as specific collective modes and probing their dynamics, we identify two distinct sound modes associated with spontaneously broken U(1) and translational symmetries. Consistent with the hydrodynamic description of superfluid smectics, longitudinal excitations propagate with finite velocities, whereas transverse perturbations exhibit diffusive behaviour. These results demonstrate how the conceptual framework of supersolidity can be used to characterize dynamic and far-from-equilibrium states.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Initialization of the lattice.
Fig. 2: Wave-packet propagation.
Fig. 3: Hydrodynamic excitations.
Fig. 4: Determination of parameters.

Similar content being viewed by others

Data availability

The datasets generated and analysed for this study are available from the corresponding author upon reasonable request.

Code availability

The conclusions of this study do not depend on code or algorithms beyond standard numerical evaluations.

References

  1. Fava, S. et al. Magnetic field expulsion in optically driven YBa2Cu3O6.48. Nature 632, 75 (2024).

    Article  Google Scholar 

  2. Li, N. et al. Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045 (2012).

    Article  ADS  Google Scholar 

  3. Wigner, E. P. in Philosophical Reflections and Syntheses (ed. Mehra, J.) 534–549 (Springer, 1995).

  4. Goldman, N. & Dalibard, J. Periodically driven quantum systems: effective Hamiltonians and engineered gauge fields. Phys. Rev. X 4, 031027 (2014).

    Google Scholar 

  5. Oka, T. & Kitamura, S. Floquet engineering of quantum materials. Annu. Rev. Condens. Matter Phys. 10, 387 (2019).

    Article  ADS  Google Scholar 

  6. Kongkhambut, P. et al. Observation of a continuous time crystal. Science 377, 670 (2022).

    Article  ADS  Google Scholar 

  7. Dogra, L. H. et al. Universal equation of state for wave turbulence in a quantum gas. Nature 620, 521 (2023).

    Article  ADS  Google Scholar 

  8. Engels, P., Atherton, C. & Hoefer, M. A. Observation of Faraday waves in a Bose-Einstein condensate. Phys. Rev. Lett. 98, 095301 (2007).

    Article  ADS  Google Scholar 

  9. Smits, J., Liao, L., Stoof, H. T. C. & van der Straten, P. Observation of a space-time crystal in a superfluid quantum gas. Phys. Rev. Lett. 121, 185301 (2018).

    Article  ADS  Google Scholar 

  10. Nguyen, J. H. V. et al. Parametric excitation of a Bose-Einstein condensate: from Faraday waves to granulation. Phys. Rev. X 9, 011052 (2019).

    Google Scholar 

  11. Zhang, Z., Yao, K. X., Feng, L., Hu, J. & Chin, C. Pattern formation in a driven Bose-Einstein condensate. Nat. Phys. 16, 652 (2020).

    Article  Google Scholar 

  12. Dupont, N. et al. Emergence of tunable periodic density correlations in a Floquet-Bloch system. Proc. Natl Acad. Sci. USA 120, e2300980120 (2023).

    Article  Google Scholar 

  13. Gross, E. P. Unified theory of interacting bosons. Phys. Rev. 106, 161 (1957).

    Article  ADS  Google Scholar 

  14. Andreev, A. F. & Lifshitz, I. M. Quantum theory of defects in crystals. Sov. Phys. JETP 29, 1107 (1969).

    ADS  Google Scholar 

  15. Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87 (2017).

    Article  ADS  Google Scholar 

  16. Li, J.-R. et al. A stripe phase with supersolid properties in spin-orbit-coupled Bose-Einstein condensates. Nature 543, 91 (2017).

    Article  ADS  Google Scholar 

  17. Recati, A. & Stringari, S. Supersolidity in ultracold dipolar gases. Nat. Rev. Phys. 5, 735 (2023).

    Article  Google Scholar 

  18. Poli, E. et al. Glitches in rotating supersolids. Phys. Rev. Lett. 131, 223401 (2023).

    Article  ADS  Google Scholar 

  19. Xiang, J. et al. Giant magnetocaloric effect in spin supersolid candidate Na2BaCo(PO4)2. Nature 625, 270 (2024).

    Article  ADS  Google Scholar 

  20. Tanzi, L. et al. Observation of a dipolar quantum gas with metastable supersolid properties. Phys. Rev. Lett. 122, 130405 (2019).

    Article  ADS  Google Scholar 

  21. Chomaz, L. et al. Long-lived and transient supersolid behaviors in dipolar quantum gases. Phys. Rev. X 9, 021012 (2019).

    Google Scholar 

  22. Böttcher, F. et al. Transient supersolid properties in an array of dipolar quantum droplets. Phys. Rev. X 9, 011051 (2019).

    Google Scholar 

  23. Norcia, M. A. et al. Two-dimensional supersolidity in a dipolar quantum gas. Nature 596, 357 (2021).

    Article  ADS  Google Scholar 

  24. Guo, M. et al. The low-energy Goldstone mode in a trapped dipolar supersolid. Nature 574, 386 (2019).

    Article  ADS  Google Scholar 

  25. Ilzhöfer, P. et al. Phase coherence in out-of-equilibrium supersolid states of ultracold dipolar atoms. Nat. Phys. 17, 356 (2021).

    Article  Google Scholar 

  26. Tanzi, L. et al. Evidence of superfluidity in a dipolar supersolid from nonclassical rotational inertia. Science 371, 1162 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  27. Norcia, M. A. et al. Can angular oscillations probe superfluidity in dipolar supersolids? Phys. Rev. Lett. 129, 040403 (2022).

    Article  ADS  Google Scholar 

  28. Biagioni, G. et al. Measurement of the superfluid fraction of a supersolid by Josephson effect. Nature 629, 773 (2024).

    Article  ADS  Google Scholar 

  29. Casotti, E. et al. Observation of vortices in a dipolar supersolid. Nature 635, 327 (2024).

    Article  Google Scholar 

  30. Hofmann, J. & Zwerger, W. Hydrodynamics of a superfluid smectic. J. Stat. Mech.: Theory Exp. 2021, 033104 (2021).

    Article  MathSciNet  Google Scholar 

  31. Blakie, P. B., Chomaz, L., Baillie, D. & Ferlaino, F. Compressibility and speeds of sound across the superfluid-to-supersolid phase transition of an elongated dipolar gas. Phys. Rev. Res. 5, 033161 (2023).

    Article  Google Scholar 

  32. Šindik, M., Zawiślak, T., Recati, A. & Stringari, S. Sound, superfluidity, and layer compressibility in a ring dipolar supersolid. Phys. Rev. Lett. 132, 146001 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  33. Natale, G. et al. Excitation spectrum of a trapped dipolar supersolid and its experimental evidence. Phys. Rev. Lett. 123, 050402 (2019).

    Article  ADS  Google Scholar 

  34. Tanzi, L. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature 574, 382 (2019).

    Article  ADS  Google Scholar 

  35. Chisholm, C. S. et al. Probing supersolidity through excitations in a spin-orbit-coupled Bose-Einstein condensate. Preprint at arxiv.org/abs/2412.13861 (2024).

  36. Yoo, C.-D. & Dorsey, A. T. Hydrodynamic theory of supersolids: variational principle, effective Lagrangian, and density-density correlation function. Phys. Rev. B 81, 134518 (2010).

    Article  ADS  Google Scholar 

  37. Liebster, N. et al. Observation of pattern stabilization in a driven superfluid. Phys. Rev. X 15, 011026 (2025).

    Google Scholar 

  38. Staliunas, K., Longhi, S. & de Valcárcel, G. J. Faraday patterns in Bose-Einstein condensates. Phys. Rev. Lett. 89, 210406 (2002).

    Article  ADS  Google Scholar 

  39. Kagan, Y. & Manakova, L. A. Formation of a condensed state with a macroscopic number of phonons in ultracold Bose gases. Phys. Rev. A 76, 023601 (2007).

    Article  ADS  Google Scholar 

  40. Fujii, K. et al. Stable-fixed-point description of square-pattern formation in driven two-dimensional Bose-Einstein condensates. Phys. Rev. A 109, L051301 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  41. Etrych, J. et al. Pinpointing Feshbach resonances and testing Efimov universalities in 39K. Phys. Rev. Res. 5, 013174 (2023).

    Article  Google Scholar 

  42. Hans, M. et al. High signal to noise absorption imaging of alkali atoms at moderate magnetic fields. Rev. Sci. Instrum. 92, 023203 (2021).

    Article  Google Scholar 

  43. Hertkorn, J. et al. Decoupled sound and amplitude modes in trapped dipolar supersolids. Phys. Rev. Res. 6, L042056 (2024).

    Article  Google Scholar 

  44. Martin, P. C., Parodi, O. & Pershan, P. S. Unified hydrodynamic theory for crystals, liquid crystals, and normal fluids. Phys. Rev. A 6, 2401 (1972).

    Article  ADS  Google Scholar 

  45. Leggett, A. J. Can a solid be ‘superfluid’? Phys. Rev. Lett. 25, 1543 (1970).

    Article  ADS  Google Scholar 

  46. Chauveau, G. et al. Superfluid fraction in an interacting spatially modulated Bose-Einstein condensate. Phys. Rev. Lett. 130, 226003 (2023).

    Article  ADS  Google Scholar 

  47. Tao, J., Zhao, M. & Spielman, I. B. Observation of anisotropic superfluid density in an artificial crystal. Phys. Rev. Lett. 131, 163401 (2023).

    Article  ADS  Google Scholar 

  48. Fruchart, M., Hanai, R., Littlewood, P. B. & Vitelli, V. Non-reciprocal phase transitions. Nature 592, 363 (2021).

    Article  ADS  Google Scholar 

  49. Sánchez-Baena, J., Politi, C., Maucher, F., Ferlaino, F. & Pohl, T. Heating a dipolar quantum fluid into a solid. Nat. Commun. 14, 1868 (2023).

    Article  Google Scholar 

  50. Viermann, C. et al. Quantum field simulator for dynamics in curved spacetime. Nature 611, 260 (2022).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank W. Zwerger for insightful comments on the hydrodynamic description. We also thank S. Stringari, A. Recati, B. Blakie, A. Smerzi, L. Pezzè and R. Klemt for positive and enlightening feedback as well as N. Antolini, N. Rasch, K. Fujii and T. Enss for discussions. This work is supported by the Deutsche Forschungsgemeinschaft (German Research Foundation) under Germany’s Excellence Strategy (EXC 2181/1 – 390900948, the Heidelberg STRUCTURES Excellence Cluster) under SFB 1225 ISOQUANT – 273811115 and by the QuantERA II Programme, which has received funding from the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 101017733) and from the Deutsche Forschungsgemeinschaft (Project No. 499183856). N.L. acknowledges support from the Studienstiftung des Deutschen Volkes.

Author information

Authors and Affiliations

  1. Kirchhoff-Institut für Physik, Universität Heidelberg, Heidelberg, Germany

    Nikolas Liebster, Marius Sparn, Elinor Kath, Jelte Duchene, Helmut Strobel & Markus K. Oberthaler

Authors
  1. Nikolas Liebster
    View author publications

    Search author on:PubMed Google Scholar

  2. Marius Sparn
    View author publications

    Search author on:PubMed Google Scholar

  3. Elinor Kath
    View author publications

    Search author on:PubMed Google Scholar

  4. Jelte Duchene
    View author publications

    Search author on:PubMed Google Scholar

  5. Helmut Strobel
    View author publications

    Search author on:PubMed Google Scholar

  6. Markus K. Oberthaler
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors conceived and designed the experiments, analysed the data and contributed to the writing of the paper.

Corresponding author

Correspondence to Nikolas Liebster.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Carlo Gabbanini and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 System Preparation.

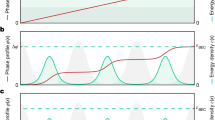
a) The experimental sequence. The oscillating line represents the scattering length. We start with a homogeneous system, and then flash on a light shift potential to imprint the lattice. A brief hold time sets the correct phase of the lattice amplitude R relative to the driving. After half a period, if superfluid phase modes are investigated, the second light shift is flashed on. Initial lattice phase deformations for excitation of the corresponding modes are included in the lattice imprint. b) The potentials used for the trap (left) and the light shift for the lattice (right). c) Mean densities throughout the drive. The contrast of the lattice oscillates, as described in eq. (20). The curves are horizontal cuts, averaged over a region of 16 μm in the center of the cloud.

Extended Data Fig. 2 Extraction of speeds of sound for superfluid and phase wavepackets.

Integrated density differences for superfluid and lattice phase defects are shown for the four times used to fit the speeds. The markers show the extracted position, enabling a comparison to the fit. Lab time of each density difference curve are shown in milliseconds.

Extended Data Fig. 3 Two-dimensional lattice deformation fields.

a) Longitudinal lattice mode. The positions of lattice maxima and minima are extracted from a reference (grey) and a perturbed lattice (red). The arrows indicate direction and magnitude of the displacement and are scaled by a factor of 10. For each time, the one-dimensional correlation with the initial state is computed, and depicted in fig. 3. b) Collective oscillation extracted in the same way for a transverse lattice mode.

Extended Data Fig. 4 System Characteristics.

a) The number of atoms varies less than 5% throughout dynamics. b) Energy in system as a function of time, extracted using the measured momentum space distribution n(k), and integrating ∫dk n(k)k2. The square at t = 0 is the value without an imprint and driving, and circles are after the imprint, measured stroboscopically at the point when the kinetic energy is maximal. c) Contrast of the stripe in x in the central region of the cloud, \(C=n{(x)}_{\max }-n{(x)}_{\min }/n{(x)}_{\max }+n{(x)}_{\min }\), extracted using a sine-fit to mean density distributions of the unperturbed system. d) Wavenumber of the lattice in x, extracted using a Fourier transform of mean density distributions. Standard errors and 1σ fit errors are either shown as the value ± its error or covered by the markers. The data in a, c, and d are derived from data sets of approximately 40 single realizations, while b uses approximately 30 single realizations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liebster, N., Sparn, M., Kath, E. et al. Supersolid-like sound modes in a driven quantum gas. Nat. Phys. 21, 1064–1070 (2025). https://doi.org/10.1038/s41567-025-02927-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02927-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing