Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Strongly interacting Hofstadter states in magic-angle twisted bilayer graphene

Nature Physics volume 21, pages 1380–1386 (2025)Cite this article

Subjects

Abstract

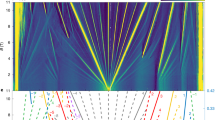
Magic-angle twisted bilayer graphene hosts a variety of strongly correlated states at partial fillings of its flat bands. In a magnetic field, these flat bands evolve into a Hofstadter spectrum renormalized by strong Coulomb interactions. Here we study the interacting Hofstadter states that spontaneously form within the topological magnetic sub-bands of an ultraclean magic-angle twisted bilayer graphene device, including symmetry-broken Chern insulator states and fractional quantum Hall states. The observed symmetry-broken Chern insulator states form a cascade, with their Chern numbers mimicking the main sequence of correlated Chern insulators. The fractional quantum Hall states form in a Jain sequence. However, they disappear at high magnetic field, in contrast to conventional fractional quantum Hall states that strengthen with increasing magnetic field. We reveal a magnetic-field-driven phase transition from composite fermion phases to a dissipative Fermi liquid. Our theoretical analysis of the magnetic sub-bands hosting the fractional quantum Hall states predicts non-uniform quantum geometric properties far from the lowest Landau level. This points towards a more natural interpretation of these states as in-field fractional Chern insulators of the magnetic sub-bands.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Transport characterization of a θ = 1.03° high-quality MATBG/WSe2 sample.
Fig. 2: Cascades of SBCI states.
Fig. 3: Finite-field Hartree–Fock calculation of the SBCI states.
Fig. 4: Unconventional FQH states in magnetic sub-bands with finite bandwidth.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data are available from the corresponding authors upon reasonable request.

Code availability

The code used for the data analysis in this study is available from the corresponding authors upon reasonable request.

References

  1. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).

    Article  ADS  Google Scholar 

  2. Wannier, G. H. A result not dependent on rationality for Bloch electrons in a magnetic field. Phys. Status Solidi B 88, 757–765 (1978).

    Article  ADS  Google Scholar 

  3. Wang, L. et al. Evidence for a fractional fractal quantum Hall effect in graphene superlattices. Science 350, 1231–1234 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  4. Spanton, E. M. et al. Observation of fractional Chern insulators in a van der Waals heterostructure. Science 360, 62–66 (2018).

    Article  ADS  Google Scholar 

  5. Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).

    Article  ADS  Google Scholar 

  6. Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).

    Article  ADS  Google Scholar 

  7. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    Article  ADS  Google Scholar 

  8. Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, eaav1910 (2019).

    Article  Google Scholar 

  9. Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).

    Article  ADS  Google Scholar 

  10. Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).

    Article  ADS  Google Scholar 

  11. Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).

    Article  ADS  Google Scholar 

  12. Xie, Y. et al. Fractional Chern insulators in magic-angle twisted bilayer graphene. Nature 600, 439–443 (2021).

    Article  ADS  Google Scholar 

  13. Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene. Nat. Phys. 17, 478–481 (2021).

    Article  Google Scholar 

  14. Yu, J. et al. Correlated Hofstadter spectrum and flavour phase diagram in magic-angle twisted bilayer graphene. Nat. Phys. 18, 825–831 (2022).

    Article  Google Scholar 

  15. Polshyn, H. et al. Topological charge density waves at half-integer filling of a moiré superlattice. Nat. Phys. 18, 42–47 (2021).

    Article  Google Scholar 

  16. He, M. et al. Symmetry-broken Chern insulators in twisted double bilayer graphene. Nano Lett. 23, 11066–11072 (2023).

    Article  ADS  Google Scholar 

  17. Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, Chern gaps and charge diffusivity in moiré graphene. Nature 592, 43–48 (2021).

    Article  Google Scholar 

  18. Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).

    Article  ADS  Google Scholar 

  19. Choi, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021).

    Article  ADS  Google Scholar 

  20. Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. 17, 710–714 (2021).

  21. Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. 20, 488–494 (2021).

    Article  ADS  Google Scholar 

  22. Wang, X. & Vafek, O. Theory of correlated Chern insulators in twisted bilayer graphene. Phys. Rev. X 14, 021042 (2023).

  23. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).

    Article  ADS  Google Scholar 

  24. Polski, R. et al. Hierarchy of symmetry breaking correlated phases in twisted bilayer graphene. Preprint at https://arxiv.org/abs/2205.05225 (2022).

  25. He, M. et al. Dynamically tunable moiré exciton Rydberg states in a monolayer semiconductor on twisted bilayer graphene. Nat. Mater. 23, 224–229 (2024).

  26. Tschirhart, C. L. et al. Imaging orbital ferromagnetism in a moiré Chern insulator. Science 372, 1323–1327 (2021).

    Article  ADS  Google Scholar 

  27. Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379–384 (2020).

    Article  ADS  Google Scholar 

  28. Lin, J.-X. et al. Spin-orbit–driven ferromagnetism at half moiré filling in magic-angle twisted bilayer graphene. Science 375, 437–441 (2022).

    Article  ADS  Google Scholar 

  29. Stepanov, P. et al. Competing zero-field Chern insulators in superconducting twisted bilayer graphene. Phys. Rev. Lett. 127, 197701 (2021).

    Article  ADS  Google Scholar 

  30. Grover, S. et al. Chern mosaic and Berry-curvature magnetism in magic-angle graphene. Nat. Phys. 18, 885–892 (2022).

    Article  Google Scholar 

  31. Tseng, C.-C. et al. Anomalous Hall effect at half filling in twisted bilayer graphene. Nat. Phys. 18, 1038–1042 (2022).

    Article  Google Scholar 

  32. Streda, P. Quantised Hall effect in a two-dimensional periodic potential. J. Phys. C 15, L1299 (1982).

    Article  ADS  Google Scholar 

  33. Kwan, Y. H. et al. Kekulé spiral order at all nonzero integer fillings in twisted bilayer graphene. Phys. Rev. X 11, 041063 (2021).

    Google Scholar 

  34. Nuckolls, K. P. et al. Quantum textures of the many-body wavefunctions in magic-angle graphene. Nature 620, 525–532 (2023).

    Article  ADS  Google Scholar 

  35. Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).

    Article  ADS  Google Scholar 

  36. Bolotin, K. I., Ghahari, F., Shulman, M. D., Stormer, H. L. & Kim, P. Observation of the fractional quantum Hall effect in graphene. Nature 462, 196–199 (2009).

    Article  ADS  Google Scholar 

  37. Du, X., Skachko, I., Duerr, F., Luican, A. & Andrei, E. Y. Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene. Nature 462, 192–195 (2009).

    Article  ADS  Google Scholar 

  38. Ghahari, F., Zhao, Y., Cadden-Zimansky, P., Bolotin, K. & Kim, P. Measurement of the ν = 1/3 fractional quantum Hall energy gap in suspended graphene. Phys. Rev. Lett. 106, 046801 (2011).

    Article  ADS  Google Scholar 

  39. Dean, C. R. et al. Multicomponent fractional quantum Hall effect in graphene. Nat. Phys. 7, 693–696 (2011).

    Article  Google Scholar 

  40. Feldman, B. E., Krauss, B., Smet, J. H. & Yacoby, A. Unconventional sequence of fractional quantum Hall states in suspended graphene. Science 337, 1196–1199 (2012).

    Article  ADS  Google Scholar 

  41. Kou, A. et al. Electron-hole asymmetric integer and fractional quantum Hall effect in bilayer graphene. Science 345, 55–57 (2014).

    Article  ADS  Google Scholar 

  42. Maher, P. et al. Tunable fractional quantum Hall phases in bilayer graphene. Science 345, 61–64 (2014).

    Article  ADS  Google Scholar 

  43. Li, J. I. A. et al. Even-denominator fractional quantum Hall states in bilayer graphene. Science 358, 648–652 (2017).

    Article  ADS  Google Scholar 

  44. Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).

    Article  ADS  Google Scholar 

  45. Huang, K. et al. Valley isospin controlled fractional quantum Hall states in bilayer graphene. Phys. Rev. X 12, 031019 (2022).

    Google Scholar 

  46. Haldane, F. D. M. Fractional quantization of the Hall effect: a hierarchy of incompressible quantum fluid states. Phys. Rev. Lett. 51, 605–608 (1983).

    Article  ADS  MathSciNet  Google Scholar 

  47. Roy, R. Band geometry of fractional topological insulators. Phys. Rev. B 90, 165139 (2014).

    Article  ADS  Google Scholar 

  48. Parker, D. et al. Field-tuned and zero-field fractional Chern insulators in magic angle graphene. Preprint at https://arxiv.org/abs/2112.13837 (2021).

  49. Wang, N. et al. Quantum-metric-induced nonlinear transport in a topological antiferromagnet. Nature 621, 487–492 (2023).

    Article  ADS  Google Scholar 

  50. Gao, A. et al. Quantum metric nonlinear Hall effect in a topological antiferromagnetic heterostructure. Science 381, 181–186 (2023).

    Article  ADS  Google Scholar 

  51. Luu, T. T. & Wörner, H. J. Measurement of the Berry curvature of solids using high-harmonic spectroscopy. Nat. Commun. 9, 916 (2018).

    Article  ADS  Google Scholar 

  52. Schüler, M. et al. Local Berry curvature signatures in dichroic angle-resolved photoelectron spectroscopy from two-dimensional materials. Sci. Adv. 6, eaay2730 (2020).

    Article  ADS  Google Scholar 

  53. de Juan, F., Grushin, A. G., Morimoto, T. & Moore, J. E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 8, 15995 (2017).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The work at UW is supported by NSF MRSEC DMR-2308979. M.H. acknowledges support from the Princeton quantum initiative. X.W. acknowledges support from the National High Magnetic Field Laboratory through NSF Grant No. DMR-2128556 and the State of Florida. B.A.B. was supported by Simons Investigator Grant No. 404513. B.A.B. and O.V. are supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative (Grant No. GBMF11070). K.W. and T.T. acknowledge support from the JSPS KAKENHI (Grant Nos. 21H05233 and 23H02052) and the World Premier International Research Center Initiative, MEXT, Japan.

Author information

Author notes

  1. These authors contributed equally: Minhao He, Xiaoyu Wang.

Authors and Affiliations

  1. Department of Physics, University of Washington, Seattle, WA, USA

    Minhao He, Jiaqi Cai, Matthew Yankowitz & Xiaodong Xu

  2. Department of Physics, Princeton University, Princeton, NJ, USA

    Minhao He, Jonah Herzog-Arbeitman & B. Andrei Bernevig

  3. National High Magnetic Field Lab, Tallahassee, FL, USA

    Xiaoyu Wang, Ran Peng & Oskar Vafek

  4. Research Center for Materials Nanoarchitectonics, National Institute for Materials Science, Tsukuba, Japan

    Takashi Taniguchi

  5. Research Center for Electronic and Optical Materials, National Institute for Materials Science, Tsukuba, Japan

    Kenji Watanabe

  6. Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, Israel

    Ady Stern

  7. Department of Materials Science and Engineering, University of Washington, Seattle, WA, USA

    Matthew Yankowitz & Xiaodong Xu

  8. Department of Physics, Florida State University, Tallahassee, FL, USA

    Oskar Vafek

Authors
  1. Minhao He
    View author publications

    Search author on:PubMed Google Scholar

  2. Xiaoyu Wang
    View author publications

    Search author on:PubMed Google Scholar

  3. Jiaqi Cai
    View author publications

    Search author on:PubMed Google Scholar

  4. Jonah Herzog-Arbeitman
    View author publications

    Search author on:PubMed Google Scholar

  5. Ran Peng
    View author publications

    Search author on:PubMed Google Scholar

  6. Takashi Taniguchi
    View author publications

    Search author on:PubMed Google Scholar

  7. Kenji Watanabe
    View author publications

    Search author on:PubMed Google Scholar

  8. Ady Stern
    View author publications

    Search author on:PubMed Google Scholar

  9. B. Andrei Bernevig
    View author publications

    Search author on:PubMed Google Scholar

  10. Matthew Yankowitz
    View author publications

    Search author on:PubMed Google Scholar

  11. Oskar Vafek
    View author publications

    Search author on:PubMed Google Scholar

  12. Xiaodong Xu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.H. fabricated the devices. M.H. and J.C. performed the measurements and analysed the data supervised by M.Y. and X.X. X.W. performed the theoretical calculations supervised by O.V., with theory inputs from J.H.-A., R.P., A.S. and B.A.B. K.W. and T.T. grew the hBN crystals. M.H., X.W., M.Y., O.V. and X.X. wrote the paper with input from all authors.

Corresponding authors

Correspondence to Minhao He, Matthew Yankowitz, Oskar Vafek or Xiaodong Xu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–18 and Notes 1–3.

Source data

Source Data Fig. 1

Source data for Fig. 1.

Source Data Fig. 2

Source data for Fig. 2.

Source Data Fig. 3

Source data for Fig. 3.

Source Data Fig. 4

Source data for Fig. 4.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, M., Wang, X., Cai, J. et al. Strongly interacting Hofstadter states in magic-angle twisted bilayer graphene. Nat. Phys. 21, 1380–1386 (2025). https://doi.org/10.1038/s41567-025-02997-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02997-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing