Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Coherent control of magnon–polaritons using an exceptional point

Nature Physics volume 21, pages 1570–1577 (2025)Cite this article

Subjects

A Publisher Correction to this article was published on 09 September 2025

This article has been updated

Abstract

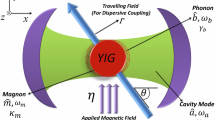
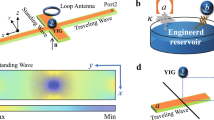
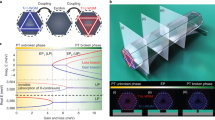
In a non-Hermitian system, the amplitude of resonant oscillations can either grow or decay in time, corresponding to a mode with either gain or loss. When two coupled modes have a specific gain–loss imbalance, an exceptional point emerges at which both eigenfrequencies and eigenmodes of the system coalesce. Exceptional points have qualitative effects on the dynamics of systems due to their topological properties, and have been used to control systems including optical microcavities, the lasing of a parity–time-symmetric waveguide and terahertz pulse generation. A challenging open problem is the fully deterministic and direct manipulation of the systems’ loss and gain on timescales relevant to the coherent control of excitations. Here we demonstrate the rapid manipulation of the complex frequency of magnon–polaritons on durations much shorter than their decay rate, allowing us to exploit non-Hermitian physics for coherent control. By dynamically encircling an exceptional point, we demonstrate population transfer between coupled magnon–polariton modes. We then drive the system directly through an exceptional point, and demonstrate that this allows the coupled system to be prepared in an equal superposition of eigenmodes. These findings establish a highly controllable hybrid platform for exploring the rich dynamical properties of non-Hermitian systems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental configuration and strong coupling.
Fig. 2: Theoretical energy landscape for two non-Hermitian coupled resonators.
Fig. 3: Population transfer by encircling an EP.
Fig. 4: Equalizing state populations by traversing beyond and back through an EP.
Fig. 5: Coherence of state after trajectories through the EP.

Similar content being viewed by others

Data availability

Data for the figures in this article are available via Zenodo at https://doi.org/10.5281/zenodo.15756785 (ref. 55). Source data are provided with this paper.

Change history

References

  1. Goryachev, M. et al. High-cooperativity cavity QED with magnons at microwave frequencies. Phys. Rev. Appl. 2, 054002 (2014).

    Article  ADS  Google Scholar 

  2. Everts, J. R. et al. Ultrastrong coupling between a microwave resonator and antiferromagnetic resonances of rare-earth ion spins. Phys. Rev. B 101, 214414 (2020).

    Article  ADS  Google Scholar 

  3. Lambert, N. J., Haigh, J. A. & Ferguson, A. J. Identification of spin wave modes in yttrium iron garnet strongly coupled to a co-axial cavity. J. Appl. Phys. 117, 053910 (2015).

    Article  ADS  Google Scholar 

  4. Tabuchi, Y. et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 113, 083603 (2014).

    Article  ADS  Google Scholar 

  5. Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014).

    Article  ADS  Google Scholar 

  6. Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K. & Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 12, 070101 (2019).

    Article  ADS  Google Scholar 

  7. Zare Rameshti, B. et al. Cavity magnonics. Phys. Rep. 979, 1–61 (2022).

    Article  MathSciNet  ADS  Google Scholar 

  8. Tabuchi, Y. et al. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. Science 349, 405 (2015).

    Article  MathSciNet  ADS  Google Scholar 

  9. Lachance-Quirion, D. et al. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 367, 425 (2020).

    Article  ADS  Google Scholar 

  10. Lambert, N. J., Haigh, J. A., Langenfeld, S., Doherty, A. C. & Ferguson, A. J. Cavity-mediated coherent coupling of magnetic moments. Phys. Rev. A 93, 021803 (2016).

    Article  ADS  Google Scholar 

  11. Wang, Y.-P. et al. Nonreciprocity and unidirectional invisibility in cavity magnonics. Phys. Rev. Lett. 123, 127202 (2019).

    Article  ADS  Google Scholar 

  12. Zhang, X., Galda, A., Han, X., Jin, D. & Vinokur, V. M. Broadband nonreciprocity enabled by strong coupling of magnons and microwave photons. Phys. Rev. Appl. 13, 044039 (2020).

    Article  ADS  Google Scholar 

  13. Zhang, D., Luo, X.-Q., Wang, Y.-P., Li, T.-F. & You, J. Q. Observation of the exceptional point in cavity magnon-polaritons. Nat. Commun. 8, 1368 (2017).

    Article  ADS  Google Scholar 

  14. Liu, H. et al. Observation of exceptional points in magnonic parity-time symmetry devices. Sci. Adv. 5, eaax9144 (2019).

    Article  ADS  Google Scholar 

  15. Zhang, X., Ding, K., Zhou, X., Xu, J. & Jin, D. Experimental observation of an exceptional surface in synthetic dimensions with magnon polaritons. Phys. Rev. Lett. 123, 237202 (2019).

    Article  ADS  Google Scholar 

  16. Cao, Y. & Yan, P. Exceptional magnetic sensitivity of 𝒫⁢𝒯-symmetric cavity magnon polaritons. Phys. Rev. B 99, 214415 (2019).

    Article  ADS  Google Scholar 

  17. Harder, M., Yao, B. M., Gui, Y. S. & Hu, C.-M. Coherent and dissipative cavity magnonics. J. Appl. Phys. 129, 201101 (2021).

    Article  ADS  Google Scholar 

  18. Hurst, H. M. & Flebus, B. Non-Hermitian physics in magnetic systems. J. Appl. Phys. 132, 220902 (2022).

    Article  ADS  Google Scholar 

  19. Qian, J. et al. Non-Hermitian control between absorption and transparency in perfect zero-reflection magnonics. Nat. Commun. 14, 3437 (2023).

    Article  ADS  Google Scholar 

  20. Wang, C. et al. Enhancement of magnonic frequency combs by exceptional points. Nat. Phys. 20, 1139 (2024).

    Article  Google Scholar 

  21. Vitanov, N. V., Rangelov, A. A., Shore, B. W. & Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 89, 015006 (2017).

    Article  ADS  Google Scholar 

  22. Xu, J. et al. Floquet cavity electromagnonics. Phys. Rev. Lett. 125, 237201 (2020).

    Article  ADS  Google Scholar 

  23. Qi, S.-F & Jing, J. Floquet generation of a magnonic NOON state. Phys. Rev. A 107, 013702 (2023).

    Article  ADS  Google Scholar 

  24. Yang, Y., Xiao, Y. & Hu, C.-M. Theory of Floquet-driven dissipative cavity magnonics. Phys. Rev. B 107, 054413 (2023).

    Article  ADS  Google Scholar 

  25. Zhang, F.-Y., Wu, Q.-C. & Yang, C.-P. Non-Hermitian shortcut to adiabaticity in Floquet cavity electromagnonics. Phys. Rev. A 106, 012609 (2022).

    Article  ADS  Google Scholar 

  26. Zhu, X., Xia, R. & Xu, L. Floquet-engineering magnonic NOON states with performance improved by soft quantum control. Quantum Inf. Process. 22, 454 (2023).

    Article  MathSciNet  ADS  Google Scholar 

  27. El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11 (2018).

    Article  Google Scholar 

  28. Özdemir, S. K., Rotter, S., Nori, F. & Yang, L. Parity-time symmetry and exceptional points in photonics. Nat. Mater. 18, 783 (2019).

    Article  ADS  Google Scholar 

  29. Peng, B. et al. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 10, 394 (2014).

    Article  Google Scholar 

  30. Dietz, B. et al. Rabi oscillations at exceptional points in microwave billiards. Phys. Rev. E 75, 027201 (2007).

    Article  ADS  Google Scholar 

  31. Doppler, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 537, 76 (2016).

    Article  ADS  Google Scholar 

  32. Partanen, M. et al. Exceptional points in tunable superconducting resonators. Phys. Rev. B 100, 134505 (2019).

    Article  ADS  Google Scholar 

  33. Xu, H., Mason, D., Jiang, L. & Harris, J. G. E. Topological energy transfer in an optomechanical system with exceptional points. Nature 537, 80 (2016).

    Article  ADS  Google Scholar 

  34. Zhang, J. et al. A phonon laser operating at an exceptional point. Nat. Photon. 12, 479 (2018).

    Article  ADS  Google Scholar 

  35. Stehmann, T., Heiss, W. D. & Scholtz, F. G. Observation of exceptional points in electronic circuits. J. Phys. A 37, 7813 (2004).

    Article  MathSciNet  ADS  Google Scholar 

  36. Choi, Y., Hahn, C., Yoon, J. W. & Song, S. H. Observation of an anti-PT-symmetric exceptional point and energy-difference conserving dynamics in electrical circuit resonators. Nat. Commun. 9, 2182 (2018).

    Article  ADS  Google Scholar 

  37. Choi, Y., Yoon, J. W., Hong, J. K., Ryu, Y. & Song, S. H. Direct observation of time-asymmetric breakdown of the standard adiabaticity around an exceptional point. Commun. Phys. 3, 1 (2020).

    Article  Google Scholar 

  38. Yoon, J. W. et al. Time-asymmetric loop around an exceptional point over the full optical communications band. Nature 562, 86 (2018).

    Article  ADS  Google Scholar 

  39. Feilhauer, J. et al. Encircling exceptional points as a non-Hermitian extension of rapid adiabatic passage. Phys. Rev. A 102, 040201 (2020).

    Article  ADS  Google Scholar 

  40. Jiang, X. et al. Coherent control of chaotic optical microcavity with reflectionless scattering modes. Nat. Phys. 20, 109–115 (2024).

    Article  Google Scholar 

  41. Schumer, A. et al. Topological modes in a laser cavity through exceptional state transfer. Science 375, 884 (2022).

    Article  ADS  Google Scholar 

  42. Ergoktas, M. S. et al. Topological engineering of terahertz light using electrically tunable exceptional point singularities. Science 376, 184 (2022).

    Article  ADS  Google Scholar 

  43. Wang, K., Dutt, A., Wojcik, C. C. & Fan, S. Topological complex-energy braiding of non-Hermitian bands. Nature 598, 59 (2021).

    Article  ADS  Google Scholar 

  44. Patil, Y. S. S. et al. Measuring the knot of non-Hermitian degeneracies and non-commuting braids. Nature 607, 271 (2022).

    Article  ADS  Google Scholar 

  45. Rao, Z. et al. Braiding reflectionless states in non-Hermitian magnonics. Nat. Phys. 20, 1904 (2024).

    Article  Google Scholar 

  46. Morris, R. G. E., van Loo, A. F., Kosen, S. & Karenowska, A. D. Strong coupling of magnons in a YIG sphere to photons in a planar superconducting resonator in the quantum limit. Sci. Rep. 7, 11511 (2017).

    Article  ADS  Google Scholar 

  47. Walker, L. R. Magnetostatic modes in ferromagnetic resonance. Phys. Rev. 105, 390 (1957).

    Article  ADS  Google Scholar 

  48. Fletcher, P., Solt, I. H. & Bell, R. Identification of the magnetostatic modes of ferrimagnetic resonant spheres. Phys. Rev. 114, 739 (1959).

    Article  ADS  Google Scholar 

  49. Harder, M. et al. Level attraction due to dissipative magnon-photon coupling. Phys. Rev. Lett. 121, 137203 (2018).

    Article  ADS  Google Scholar 

  50. Gilary, I., Mailybaev, A. A. & Moiseyev, N. Time-asymmetric quantum-state-exchange mechanism. Phys. Rev. A 88, 010102 (2013).

    Article  ADS  Google Scholar 

  51. Uzdin, R., Mailybaev, A. & Moiseyev, N. On the observability and asymmetry of adiabatic state flips generated by exceptional points. J. Phys. A 44, 435302 (2011).

    Article  MathSciNet  ADS  Google Scholar 

  52. Nasari, H. et al. Observation of chiral state transfer without encircling an exceptional point. Nature 605, 256 (2022).

    Article  ADS  Google Scholar 

  53. Hassan, A. U. et al. Chiral state conversion without encircling an exceptional point. Phys. Rev. A 96, 052129 (2017).

    Article  ADS  Google Scholar 

  54. Znojil, M. Passage through exceptional point: case study. Proc. Math. Phys. Eng. Sci. 476, 20190831 (2020).

    MathSciNet  Google Scholar 

  55. Lambert, N. J., Schumer, A., Longdell, J. J., Rotter, S. & Schwefel, H. G. L. Data for figures in ‘Coherent control of magnon-polaritons using an exceptional point’. Zenodo https://doi.org/10.5281/zenodo.15756785 (2025).

Download references

Acknowledgements

N.J.L. is supported by Marsden Fund grant number 24-UOO-153. N.J.L acknowledges discussions with J. Squire.

Author information

Authors and Affiliations

  1. Department of Physics, University of Otago, Dunedin, New Zealand

    N. J. Lambert, J. J. Longdell & H. G. L. Schwefel

  2. The Dodd–Walls Centre for Photonic and Quantum Technologies, Dunedin, New Zealand

    N. J. Lambert, J. J. Longdell & H. G. L. Schwefel

  3. Institute for Theoretical Physics, Vienna University of Technology (TU Wien), Vienna, Austria

    A. Schumer & S. Rotter

Authors
  1. N. J. Lambert
    View author publications

    Search author on:PubMed Google Scholar

  2. A. Schumer
    View author publications

    Search author on:PubMed Google Scholar

  3. J. J. Longdell
    View author publications

    Search author on:PubMed Google Scholar

  4. S. Rotter
    View author publications

    Search author on:PubMed Google Scholar

  5. H. G. L. Schwefel
    View author publications

    Search author on:PubMed Google Scholar

Contributions

N.J.L. conceptualized the experiment and performed the implementation and measurement. The paper was written by N.J.L. with input from all authors. A.S. and S.R. carried out the theoretical calculations and provided conceptual input. The work was supervised by J.J.L., S.R. and H.G.L.S.

Corresponding author

Correspondence to N. J. Lambert.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Zhenghua An, Benedetta Flebus and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1 and 2 and Discussion.

Supplementary Data 1

Data and model for Supplementary Fig. 1.

Supplementary Data 2

Data for all τ values in Supplementary Fig. 2.

Source data

Source Data Fig. 1

Plotted data.

Source Data Fig. 3

Plotted data.

Source Data Fig. 4

Plotted data.

Source Data Fig. 5

Plotted data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lambert, N.J., Schumer, A., Longdell, J.J. et al. Coherent control of magnon–polaritons using an exceptional point. Nat. Phys. 21, 1570–1577 (2025). https://doi.org/10.1038/s41567-025-02998-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02998-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing