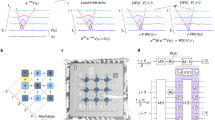
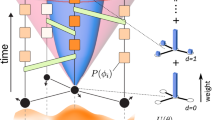
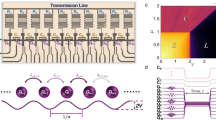
Abstract
Quantum circuits with local unitaries offer a platform to explore many-body quantum dynamics in discrete time. Their locality makes them suitable for current processors, but verification at scale is difficult for non-integrable systems. Here we study dual-unitary circuits, which are maximally chaotic yet permit exact analytical solutions for certain correlation functions. Using improved noise-learning and error-mitigation methods, we show that a superconducting quantum processor with 91 qubits is able to accurately simulate these correlators. We then perturb the circuits away from the dual-unitary point and benchmark the dynamics against tensor-network simulations. These results establish error-mitigated digital quantum simulation on pre-fault-tolerant processors as a reliable tool to explore emergent quantum many-body phases.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The datasets generated and analysed during this study are available via Figshare at https://doi.org/10.6084/m9.figshare.29069759 (ref. 60).
Code availability
Code for tensor-network simulations of the noiseless quantum circuits is available via Figshare at https://doi.org/10.6084/m9.figshare.29069759 (ref. 60).
References
Miessen, A., Ollitrault, P. J., Tacchino, F. & Tavernelli, I. Quantum algorithms for quantum dynamics. Nat. Comput. Sci. 3, 25–37 (2023).
Fisher, M. P. A., Khemani, V., Nahum, A. & Vijay, S. Random quantum circuits. Annu. Rev. Condens. Matter Phys. 14, 335–379 (2023).
Hangleiter, D. & Eisert, J. Computational advantage of quantum random sampling. Rev. Modern Phys. 95, 035001 (2023).
Li, Y., Chen, X. & Fisher, M. P. A. Quantum zeno effect and the many-body entanglement transition. Phys. Rev. B 98, 205136 (2018).
Skinner, B., Ruhman, J. & Nahum, A. Measurement-induced phase transitions in the dynamics of entanglement. Phys. Rev. X 9, 031009 (2019).
Mi, X. et al. Time-crystalline eigenstate order on a quantum processor. Nature 601, 531–536 (2022).
Sünderhauf, C., Pérez-García, D., Huse, D. A., Schuch, N. & Cirac, J. I. Localization with random time-periodic quantum circuits. Phys. Rev. B 98, 134204 (2018).
Garratt, S. J. & Chalker, J. T. Many-body delocalization as symmetry breaking. Phys. Rev. Lett. 127, 026802 (2021).
Morningstar, A., Colmenarez, L., Khemani, V., Luitz, D. J. & Huse, D. A. Avalanches and many-body resonances in many-body localized systems. Phys. Rev. B 105, 174205 (2022).
Vanicat, M., Zadnik, L. & Prosen, T. Integrable trotterization: local conservation laws and boundary driving. Phys. Rev. Lett. 121, 030606 (2018).
Chan, A., De Luca, A. & Chalker, J. T. Solution of a minimal model for many-body quantum chaos. Phys. Rev. X 8, 041019 (2018).
Bertini, B., Kos, P. & Prosen, T. Exact spectral form factor in a minimal model of many-body quantum chaos. Phys. Rev. Lett. 121, 264101 (2018).
Bertini, B., Kos, P. & Prosen, T. Random matrix spectral form factor of dual-unitary quantum circuits. Commun. Math. Phys. 387, 597–620 (2021).
Bertini, B., Kos, P. & Prosen, T. Exact correlation functions for dual-unitary lattice models in 1 + 1 dimensions. Phys. Rev. Lett. 123, 210601 (2019).
Gopalakrishnan, S. & Lamacraft, A. Unitary circuits of finite depth and infinite width from quantum channels. Phys. Rev. B 100, 064309 (2019).
Piroli, L., Bertini, B., Cirac, J. I. & Prosen, T. Exact dynamics in dual-unitary quantum circuits. Phys. Rev. B 101, 094304 (2020).
Bertini, B., Kos, P. & Prosen, T. Operator entanglement in local quantum circuits I: chaotic dual-unitary circuits. SciPost Physics 8, 067 (2020).
Ippoliti, M. & Khemani, V. Postselection-free entanglement dynamics via spacetime duality. Phys. Rev. Lett. 126, 060501 (2021).
Suzuki, R., Mitarai, K. & Fujii, K. Computational power of one-and two-dimensional dual-unitary quantum circuits. Quantum 6, 631 (2022).
Claeys, P. W. & Lamacraft, A. Maximum velocity quantum circuits. Phys. Rev. Res. 2, 033032 (2020).
Bertini, B. & Piroli, L. Scrambling in random unitary circuits: exact results. Phys. Rev. B 102, 064305 (2020).
Chertkov, E. et al. Holographic dynamics simulations with a trapped-ion quantum computer. Nat. Phys. 18, 1074–1079 (2022).
Bertini, B., Kos, P. & Prosen, T. Entanglement spreading in a minimal model of maximal many-body quantum chaos. Phys. Rev. X 9, 021033 (2019).
Zhou, T. & Harrow, A. W. Maximal entanglement velocity implies dual unitarity. Phys. Rev. B 106, L201104 (2022).
Mi, X. et al. Information scrambling in quantum circuits. Science 374, 1479–1483 (2021).
Keenan, N., Robertson, N. F., Murphy, T., Zhuk, S. & Goold, J. Evidence of Kardar–Parisi–Zhang scaling on a digital quantum simulator. npj Quantum Inf. 9, 72 (2023).
Kim, Y. et al. Evidence for the utility of quantum computing before fault tolerance. Nature 618, 500–505 (2023).
Robledo-Moreno, J. et al. Chemistry beyond the scale of exact diagonalization on a quantum-centric supercomputer. Sci. Adv. 11, eadu9991 (2025).
Shinjo, K., Seki, K., Shirakawa, T., Sun, R.-Y. & Yunoki, S. Unveiling clean two-dimensional discrete time quasicrystals on a digital quantum computer. Preprint at https://arxiv.org/abs/2403.16718 (2024).
Farrell, R. C., Illa, M., Ciavarella, A. N. & Savage, M. J. Quantum simulations of hadron dynamics in the schwinger model using 112 qubits. Phys. Rev. D 109, 114510 (2024).
Shtanko, O. et al. Uncovering local integrability in quantum many-body dynamics. Nat. Commun. 16, 2552 (2025).
Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509 (2017).
Li, Y. & Benjamin, S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7, 021050 (2017).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Van Den Berg, E., Minev, Z. K., Kandala, A. & Temme, K. Probabilistic error cancellation with sparse pauli–lindblad models on noisy quantum processors. Nat. Phys. 19, 1116–1121 (2023).
Zimborás, Z. et al. Myths around quantum computation before full fault tolerance: what no-go theorems rule out and what they don’t. Preprint at https://arxiv.org/abs/2501.05694 (2025).
Govia, L. et al. Bounding the systematic error in quantum error mitigation due to model violation. PRX Quantum 6, 010354 (2025).
Filippov, S., Leahy, M., Rossi, M. A. C. & García-Pérez, G. Scalable tensor-network error mitigation for near-term quantum computing. Preprint at https://arxiv.org/abs/2307.11740 (2023).
Filippov, S. N., Maniscalco, S. & García-Pérez, G. Scalability of quantum error mitigation techniques: from utility to advantage. Preprint at https://arxiv.org/abs/2403.13542 (2024).
Prosen, T. General relation between quantum ergodicity and fidelity of quantum dynamics. Phys. Rev. E 65, 036208 (2002).
Akila, M., Waltner, D., Gutkin, B. & Guhr, T. Particle-time duality in the kicked ising spin chain. J. Phys. A 49, 375101 (2016).
Huang, H.-Y., Kueng, R. & Preskill, J. Predicting many properties of a quantum system from very few measurements. Nat. Phys. 16, 1050–1057 (2020).
Glos, A. et al. Adaptive POVM implementations and measurement error mitigation strategies for near-term quantum devices. Preprint at https://arxiv.org/abs/2208.07817 (2022).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Knill, E. Fault-tolerant postselected quantum computation: threshold analysis. Preprint at https://arxiv.org/abs/quant-ph/0404104 (2004).
Wallman, J. J. & Emerson, J. Noise tailoring for scalable quantum computation via randomized compiling. Phys. Rev. A 94, 052325 (2016).
Hashim, A. et al. Randomized compiling for scalable quantum computing on a noisy superconducting quantum processor. Phys. Rev. X 11, 041039 (2021).
Chen, S. et al. The learnability of Pauli noise. Nat. Commun. 14, 52 (2023).
Chen, S., Zhang, Z., Jiang, L. & Flammia, S. T. Efficient self-consistent learning of gate set Pauli noise. Preprint at https://arxiv.org/abs/2410.03906 (2024).
Kim, Y. et al. Error mitigation with stabilized noise in superconducting quantum processors. Nat. Commun. 16, 8439 (2025).
Ljubotina, M., Zadnik, L. & Prosen, T. Ballistic spin transport in a periodically driven integrable quantum system. Phys. Rev. Lett. 122, 150605 (2019).
Long, D. M., Crowley, P. J. D., Khemani, V. & Chandran, A. Phenomenology of the prethermal many-body localized regime. Phys. Rev. Lett. 131, 106301 (2023).
Eddins, A., Tran, M. C. & Rall, P. Lightcone shading for classically accelerated quantum error mitigation. Preprint at https://arxiv.org/abs/2409.04401 (2024).
Robertson, N. F. et al. Tensor network enhanced dynamic multiproduct formulas. PRX Quantum 6, 020360 (2025).
Stehlik, J. et al. Tunable coupling architecture for fixed-frequency transmon superconducting qubits. Phys. Rev. Lett. 127, 080505 (2021).
Wack, A. et al. Scale, quality, and speed: three key attributes to measure the performance of near-term quantum computers. Preprint at https://arxiv.org/abs/2110.14108 (2021).
Rajagopala, A. D. et al. Hardware-assisted parameterized circuit execution. Preprint at https://arxiv.org/abs/2409.03725 (2024).
Van Den Berg, E., Minev, Z. K. & Temme, K. Model-free readout-error mitigation for quantum expectation values. Phys. Rev. A 105, 032620 (2022).
Tsubouchi, K., Sagawa, T. & Yoshioka, N. Universal cost bound of quantum error mitigation based on quantum estimation theory. Phys. Rev. Lett. 131, 210601 (2023).
Data and code for: dynamical simulations of many-body quantum chaos on a quantum computer. Figshare https://doi.org/10.6084/m9.figshare.29069759 (2025).
Acknowledgements
A.E., Y.K. and A.K. thank S. Bravyi for introducing DU circuits to them. M.A.C.R., Z.Z., G.G.P. and J.G. thank L. Piroli for useful discussions. We thank R. Malik for enabling device access. We thank A. Seif, D. Layden, E. van den Berg and L. Govia for feedback on the manuscript. I.T., F.T. and L.E.F. thank S. Wörner, A. Carrera Vázquez and D. Egger for helpful discussions. M.L., D.F., M.A.C.R., F.P., B.S., Z.Z., S.M., J.G., G.G.-P. and S.N.F. are grateful to E.-M. Borrelli, D. Cavalcanti, S. Mangini, M. Cattaneo, K. Korhonen, H. Vappula and J. Malmi for helpful discussions. We acknowledge the EuroHPC Joint Undertaking for awarding us the projects EHPC-DEV-2024D04-042, providing access to Leonardo at CINECA, Italy, and EHPC-DEV-2023D08-016, providing access to Karolina at IT4Innovations, Czech Republic. L.E.F. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 955479 (MOQS – Molecular Quantum Simulations). I.T. acknowledges support from NCCR MARVEL, funded by the Swiss National Science Foundation. S.D. acknowledges support through the SFI-IRC Pathway Grant 22/PATH-S/10812. J.G. is supported by a Royal Society University Research Fellowship and thanks S. Pappalardi for inspirational discussions.
Author information
Authors and Affiliations
Contributions
The Algorithmiq team (M.L., D.F., M.A.C.R., F.P., B.S., Z.Z., S.M., J.G., G.G.P. and S.N.F.) led the design and implementation of TEM and TN simulations. The IBM Quantum team (L.E.F., A.E., N.K., Y.K., A.H., F.T., I.T. and A.K.) led the experimental implementation, noise characterization and the hardware calibrations. L.E.F. performed the experiments with support from the IBM team. M.L. implemented the TEM with support from the Algorithmiq team, D.F. implemented the tensor-network simulations with support from the Algorithmiq team. S.N.F. and G.G.-P. conceived TEM. The Algorithmiq, TCD (M.L., N.K., S.D. and J.G.) and IBM teams contributed to the design of the experiments, circuits and tensor-network simulations, as well as data analysis and paper writing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Bruno Bertini and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementay Discussion, with Supplementary Figs. 1–19 and Table 1.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fischer, L.E., Leahy, M., Eddins, A. et al. Dynamical simulations of many-body quantum chaos on a quantum computer. Nat. Phys. (2026). https://doi.org/10.1038/s41567-025-03144-9
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41567-025-03144-9
This article is cited by
-
Mitigated chaos
Nature Physics (2026)