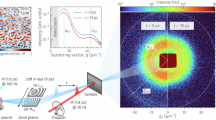
Abstract
Ultrafast optical laser-based techniques have enabled the probing of atomistic processes at their intrinsic temporal scales with femto- and attosecond resolution. However, the long wavelengths of optical lasers have prevented their interrogation and manipulation with nanoscale spatial specificity. Advances in hard X-ray free-electron lasers have enabled progress in developing X-ray transient-grating spectroscopy, a technique that aims to coherently control elementary excitations with nanoscale X-ray standing waves. Thus far, the realization of this technique at the nanoscale has been a challenge. Here we demonstrate X-ray transient-grating spectroscopy with spatial periods of the order of 10 nm via the subfemtosecond synchronization of two hard X-ray pump pulses at a precisely controlled crossing angle. This creates a thermal grating and preferentially excites coherent longitudinal acoustic phonon modes with the transient-grating wavevector. On probing with a third, variably delayed, X-ray pulse with the same photon energy, time-and-wavevector-resolved measurements of the modulation of the induced scattering intensity provide evidence of ballistic thermal transport at nanometre scales. These results highlight the potential of X-ray transient gratings as a powerful platform for studying nanoscale transport in condensed matter and the coherent control of nanoscale dynamics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data supporting the findings of the study are included in the main text and supplementary information files. Source data have been deposited in the Stanford Digital Repository at https://purl.stanford.edu/zy110hn7917 (ref. 50). Other data are available from the corresponding author upon request.
Code availability
The code used to produce the figures in the main text, extended data and supplementary information files has been deposited in the Stanford Digital Repository at https://purl.stanford.edu/zy110hn7917 (ref. 50). The code used to access and process the raw experimental data is available from the corresponding author upon request.
References
Simons, K. & Sampaio, J. L. Membrane organization and lipid rafts. Cold Spring Harb. Perspect. Biol. 3, a004697 (2011).
Meena, J. S., Sze, S. M., Chand, U. & Tseng, T.-Y. Overview of emerging nonvolatile memory technologies. Nanoscale Res. Lett. 9, 526 (2014).
Biswas, A. et al. Advances in top–down and bottom–up surface nanofabrication: techniques, applications & future prospects. Adv. Colloid Interface Sci. 170, 2–27 (2012).
Krivanek, O. L. et al. Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy. Nature 464, 571–574 (2010).
Kukura, P., McCamant, D. W. & Mathies, R. A. Femtosecond stimulated Raman spectroscopy. Annu. Rev. Phys. Chem. 58, 461–488 (2007).
Teitelbaum, S. W. et al. Frequency-selective excitation of high-wavevector phonons. Appl. Phys. Lett. 113, 171901 (2018).
Li, X. et al. Terahertz field–induced ferroelectricity in quantum paraelectric SrTiO3. Science 364, 1079–1082 (2019).
Kogar, A. et al. Light-induced charge density wave in LaTe3. Nat. Phys. 16, 159–163 (2020).
Salikhov, R. et al. Coupling of terahertz light with nanometre-wavelength magnon modes via spin–orbit torque. Nat. Phys. 19, 529–535 (2023).
Bedzyk, M. J. & Cheng, L. X-ray standing wave studies of minerals and mineral surfaces: principles and applications. Rev. Mineral. Geochem. 49, 221–266 (2002).
Fadley, C. S. Hard X-ray photoemission with angular resolution and standing-wave excitation. J. Electron Spectrosc. Relat. Phenom. 190, 165–179 (2013).
Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 4, 641–647 (2010).
Pile, D. First light from SACLA. Nat. Photonics 5, 456–457 (2011).
Milne, C. J. et al. SwissFEL: the Swiss X-ray free electron laser. Appl. Sci. 7, 720 (2017).
Weise, H. et al. Commissioning and first lasing of the European XFEL. In Proc. 38th International Free Electron Laser Conference (FEL 2017) (eds Bishofberger, K. et al) 9–13 (JACoW, 2017).
Rouxel, J. R. et al. Hard X-ray transient grating spectroscopy on bismuth germanate. Nat. Photonics 15, 499–503 (2021).
Chergui, M., Beye, M., Mukamel, S., Svetina, C. & Masciovecchio, C. Progress and prospects in nonlinear extreme-ultraviolet and X-ray optics and spectroscopy. Nat. Rev. Phys. 5, 578–596 (2023).
Ambrosetti, A., Ferri, N., DiStasio Jr, R. A. & Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 351, 1171–1176 (2016).
Miedaner, P. R. et al. Excitation and detection of coherent nanoscale spin waves via extreme ultraviolet transient gratings. Sci. Adv. 10, eadp6015 (2024).
Hayes, R., Warr, G. G. & Atkin, R. Structure and nanostructure in ionic liquids. Chem. Rev. 115, 6357–6426 (2015).
Bencivenga, F. et al. Nanoscale transient gratings excited and probed by extreme ultraviolet femtosecond pulses. Sci. Adv. 5, 5805 (2019).
Foglia, L. et al. Extreme ultraviolet transient gratings: a tool for nanoscale photoacoustics. Photoacoustics 29, 100453 (2023).
Bencivenga, F. et al. Four-wave mixing experiments with extreme ultraviolet transient gratings. Nature 520, 205–208 (2015).
Foglia, L. et al. First evidence of purely extreme-ultraviolet four-wave mixing. Phys. Rev. Lett. 120, 263901 (2018).
Ferrari, E. et al. All hard X-ray transient grating spectroscopy. Commun. Phys. 8, 257 (2025).
de Vera, P. & Garcia-Molina, R. Electron inelastic mean free paths in condensed matter down to a few electronvolts. J. Phys. Chem. C 123, 2075–2083 (2019).
Huang, Y. et al. Nanometer-scale acoustic wave packets generated by stochastic core-level photoionization events. Phys. Rev. X 14, 041010 (2024).
Chollet, M. et al. The X-ray pump–probe instrument at the Linac Coherent Light Source. J. Synchrotron Radiat. 22, 503–507 (2015).
Li, H. et al. Generation of highly mutually coherent hard-X-ray pulse pairs with an amplitude-splitting delay line. Phys. Rev. Res. 3, 043050 (2021).
Knoester, J. & Mukamel, S. Transient gratings, four-wave mixing and polariton effects in nonlinear optics. Phys. Rep. 205, 1–58 (1991).
Shvyd’ko, Yu. X-ray Optics: High-Energy-Resolution Applications (Springer Science & Business Media, 2004).
Medvedev, N. Femtosecond X-ray induced electron kinetics in dielectrics: application for fel-pulse-duration monitor. Appl. Phys. B 118, 417–429 (2015).
Kaiser, A., Rethfeld, B., Vicanek, M. & Simon, G. Microscopic processes in dielectrics under irradiation by subpicosecond laser pulses. Phys. Rev. B 61, 11437 (2000).
Ishidate, T., Sasaki, S. & Inoue, K. Brillouin scattering of SrTiO3 under high pressure. High Press. Res. 1, 53–65 (1988).
Shayduk, R. et al. Femtosecond X-ray diffraction study of multi-Thz coherent phonons in SrTiO3. Appl. Phys. Lett. 120, 202203 (2022).
Hofmann, F., Short, M. P. & Dennett, C. A. Transient grating spectroscopy: an ultrarapid, nondestructive materials evaluation technique. MRS Bull. 44, 392–402 (2019).
Martelli, V., Jiménez, J. L., Continentino, M., Baggio-Saitovitch, E. & Behnia, K. Thermal transport and phonon hydrodynamics in strontium titanate. Phys. Rev. Lett. 120, 125901 (2018).
Maznev, A. A., Johnson, J. A. & Nelson, K. A. Onset of nondiffusive phonon transport in transient thermal grating decay. Phys. Rev. B 84, 195206 (2011).
Fumega, A. O., Fu, Y., Pardo, V. & Singh, D. J. Understanding the lattice thermal conductivity of SrTiO3 from an ab initio perspective. Phys. Rev. Mater. 4, 033606 (2020).
Fainozzi, D. et al. Stimulated Brillouin scattering in the time domain at 1 nm−1 wave vector. Phys. Rev. Lett. 132, 033802 (2024).
Henighan, T. et al. Generation mechanism of terahertz coherent acoustic phonons in Fe. Phys. Rev. B 93, 220301 (2016).
Jia, C.-L. et al. Nanodomains and nanometer-scale disorder in multiferroic bismuth ferrite single crystals. Acta Mater. 82, 356–368 (2015).
Kozina, M. et al. Terahertz-driven phonon upconversion in SrTiO3. Nat. Phys. 15, 387–392 (2019).
Decking, W. et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 14, 391–397 (2020).
Raubenheimer, T. The LCLS-II-HE, a high energy upgrade of the LCLS-II. In Proc. 60th ICFA Advanced Beam Dynamics Workshop on Future Light Sources (eds Chin, Y.-H. et al.) MOP1WA02 (JACoW, 2018).
Hara, T. et al. Two-colour hard X-ray free-electron laser with wide tunability. Nat. Commun. 4, 2919 (2013).
Lutman, A. et al. Experimental demonstration of femtosecond two-color X-ray free-electron lasers. Phys. Rev. Lett. 110, 134801 (2013).
Zhu, D. et al. Performance of a beam-multiplexing diamond crystal monochromator at the Linac Coherent Light Source. Rev. Sci. Instrum. 85, 6 (2014).
Mozzanica, A. et al. The JUNGFRAU detector for applications at synchrotron light sources and XFELs. Synchrotron Radiat. News 31, 16–20 (2018).
Li, H. et al. Experiment data for hard X-ray transient grating beamtime 2024. Stanford Digital Repository http://purl.stanford.edu/zy110hn7917 (2025).
Acknowledgements
Financial support from the US Department of Energy (DOE), Office of Basic Energy Sciences, Gas-Phase Chemical Physics Program (Award Nos. DE-SC0022222 and FWP-100778 to H.L. and M.I.) is gratefully acknowledged. The contributions by N.B., P.R.M., Z.Z., K.A.N. and A.A.M. were supported by the DOE, Office of Science, Office of Basic Energy Sciences (Award No. DE-SC0019126). L.Z., M.T. and D.A.R. were supported by the US DOE, Office of Science, Office of Basic Energy Sciences through the Division of Materials Sciences and Engineering (Contract No. DE-AC02-76SF00515). The contributions by C.O. were supported by the AMOS programme within the Chemical Sciences, Geosciences, and Biosciences Division, DOE, Office of Basic Energy Sciences. The contributions by Y.S., S. Song, T.S., N.W., S. She, M.-L.N., M.D.B., V.E., J.B.H. and D.Z. were supported by the US DOE, Office of Science, Office of Basic Energy Sciences (Contract No. DE-AC02-76SF00515). Use of the LCLS, SLAC National Accelerator Laboratory, is supported by the US DOE, Office of Science, Office of Basic Energy Sciences (Contract No. DE-AC02-76SF00515).
Author information
Authors and Affiliations
Contributions
Data curation: C.C.O.-S., D.H., H.L., L.Z., N.B., N.W., P.R.M., S.D., S. She, S. Song, Y.S., T.S. Formal analysis: A.A.M., D.A.R., D.H., D.Z., H.L., L.F., L.Z., M.T., N.B., N.W., P.R.M., S.D., S.T. Funding acquisition: D.Z., M.I., K.A.N. Investigation: A.A.M., C.C.O.-S., C.D., D.A.R., D.H., D.Z., H.L., J.B.H., J.V.-C., K.A.N., L.F., L.Z., M.D.B., M.-L.N., N.B., N.W., P.R.M., S.D., S. She, S. Song, S.T., T.S., V.E., Y.S., Z.Z. Methodology: A.A.M., C.C.O.-S., D.A.R., D.Z., H.L., L.F., M.D.B., M.T., S. She, S. Song, S.T., T.S., V.E., Y.S. Project administration: D.Z., S. Song. Resources: C.D., D.Z., J.V.-C., K.A.N., M.-L.N., N.B., Z.Z. Software: V.E. Supervision: D.Z., J.B.H., K.A.N., M.I. Writing – original draft: A.A.M., D.A.R., D.Z., H.L., L.F., S.T. Writing – review & editing: A.A.M., D.A.R., D.Z., H.L., L.F., M.I., S.T.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Schematics of experimental setup.
(a) The layout of X-ray optics, sample and detector inside the experiment hutch. (b) and (c) are X-ray trajectories in the x-z and y-z plane downstream of the SDO. (d) Pump and probe pulse positions on grating, G. Image taken with cameras during the experiment. The rectangles are independent gratings on the same diamond substrate. (e) Relative orientation of the X-ray pulses and the sample. The x, y, and z axes follow the same convention as in (a) and Fig. 1(b). k1 and k2 denote the wavevectors of the two pump pulses within the x-z plane, while k3 corresponds to the probe pulse, which lies largely within the y-z plane. k4 represents the scattered photon wavevector that satisfies the phase-matching condition. The green arrows indicate the (010) and (100) directions of the STO crystal lattice, with n marking the surface normal. The lightly sketched parallelograms inside the orange cube depict the atomic planes associated with the (220) reciprocal lattice of STO. The red elongated ellipses illustrate the intensity profile of the X-ray pump interference pattern, with the spatial periodicity oriented along the x axis.
Extended Data Fig. 2 Angular dependence of efficiency.
(a), (b) and (c) are angular dependences of the diffraction efficiency measured for the Bragg peak (black) and the TG peaks. For detailed comparison, the horizontal axis Δϕ is the relative angle with respect to the peak position of each curve. The number in the legend shows the corresponding XTG wavelength ΛTG. The ± kTG on the top left corner indicates the angular relation of the TG peak with respect to the Bragg peak and is the same as that in Fig. 2.
Extended Data Fig. 3 Comparison of Bragg diffraction efficiency of simulation versus measurement.
The blue stars show measured STO (220) Bragg diffraction efficiency for different sample rotation angles ϕ. The black curve is the simulation result assuming a perfect crystal within the X-ray illuminated region.
Extended Data Fig. 4 XTG-enhanced intensity modulation.
In (a), the solid lines are line cuts of Figure 2(c) and (d) along lines of first maxima in τ for each q. The dashed lines are linear fits of the corresponding solid lines for q < 0.05 Å−1. (b) is the ratio between the measured intensity modulation maxima \({r}_{\exp }-1\) shown in solid lines in (a), versus the linear fit shown in dashed lines rfit − 1 in (a).
Extended Data Fig. 5 Pump pulse trajectory and mirror angle calibration.
(a) shows the trajectory of one pump pulse between G and the sample. For a given grating-sample distance d0 = 6 m grating diffraction angle α0/2, beam position on the sample plane η, and mirror angle α, one can uniquely determine the total path length l1 + l2. In the ideal case, η = 0, and α is determined by the targeted ΛTG. (b) shows the dependence of l1 + l2 of α around the ideal value of 0.15∘ for η ∈ [ − 2, 2] μm. The green vertical lines mark the boundary of Δα = ± 0.01∘. The red horizontal lines mark the boundary of Δ(l1 + l2) = ± 0.3 μm. A beam overlap accuracy of ∣Δη∣≤2 μm, and a mirror angle uncertainty of ∣Δα∣≤0.01∘ guarantee a synchronization better than 1 fs between the two pump pulses. (c) Schematics of X-ray partial reflection by the mirror (purple). The rotation center, marked with the red dot, lies at the center of the mirror reflection surface. The X-ray beam size is L, and the distance between beam center and rotation center is l0 ≈ L/2. For a grazing incidence angle α, part of the X-ray beam is reflected by the mirror. (d) shows the X-ray beam profile on the sample plane. The upper edge of the reflected X-ray is separated from O by S2, while the lower edge of the un-reflected X-ray is separated from O by S1. (e) and (f) show the mean error between simulated and measured S2 – S1 for M1 and M2 respectively over a range of mirror-sample distance D, and motor angle offset αoff. The measurement data are documented in Extended Data Table 1. The purple ellipses in (c) and (d) mark the regions with a value smaller than twice the global minimum. The projection of the ellipse gives the uncertainties of D and αoff. The mirror angle offset αoff is the difference between the grazing incident angle α and the recorded motor feedback value αf = α + αoff. The accuracy of αf is 0.000765∘ according to the spec. Therefore, the uncertainty of α equals to that of αoff, which was determined to be 0.003∘.
Extended Data Fig. 6 Detector Q map calibration.
(a) Example of the scattering intensity of the Bragg peak from SrTiO3 measured with the area detector in our experiment. The axis labels are the pixel indexes. (b) shows the LaB6 powder scattering rings from the probe pulse, overlapped with the documented ring positions (solid curves) with the calibrated detector position and distance. The numbers indicate the angular wavenumber measured in Å−1 for the documented ring positions for LaB6. (c) and (d) show the LaB6 powder scattering rings from the two crossing pump pulses, overlapped with the documented ring positions with the calibrated detector position and distance.
Extended Data Fig. 7 Detector q map of the region of interest.
(a) The Q value for each pixel within the region of interest containing the Bragg peak and TG peaks. The axis labels are pixel indexes as shown in Extended Data Figure 6. (b), (c) and (d) are q maps of TG measurements for ΛTG = 9.2 and 11.8 nm. The black dashed lines are guiding lines for minimal q in each plot. The red box is the location of the TG peak.
Extended Data Fig. 8 X-ray diffuse scattering fitting.
(a) and (c) are measured r(q, τ) respectively for − kTG and kTG, excluding TG peaks. (b) and (d) are fitting results with Equation (E-2) for (a) and (c) respectively. The black dashed lines in (a) and (c) are guiding lines, indicating the temporal maximum for each q with the fitting results.
Supplementary information
Supplementary Information
Supplementary Notes 1–3.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, H., Wang, N., Zhang, L. et al. Nanoscale ultrafast lattice modulation with a free-electron laser. Nat. Phys. (2026). https://doi.org/10.1038/s41567-025-03161-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41567-025-03161-8