Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A site-resolved two-dimensional quantum simulator with hundreds of trapped ions

Nature volume 630, pages 613–618 (2024)Cite this article

Subjects

Abstract

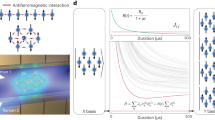
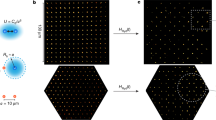
A large qubit capacity and an individual readout capability are two crucial requirements for large-scale quantum computing and simulation1. As one of the leading physical platforms for quantum information processing, the ion trap has achieved a quantum simulation of tens of ions with site-resolved readout in a one-dimensional Paul trap2,3,4 and of hundreds of ions with global observables in a two-dimensional (2D) Penning trap5,6. However, integrating these two features into a single system is still very challenging. Here we report the stable trapping of 512 ions in a 2D Wigner crystal and the sideband cooling of their transverse motion. We demonstrate the quantum simulation of long-range quantum Ising models with tunable coupling strengths and patterns, with or without frustration, using 300 ions. Enabled by the site resolution in the single-shot measurement, we observe rich spatial correlation patterns in the quasi-adiabatically prepared ground states, which allows us to verify quantum simulation results by comparing the measured two-spin correlations with the calculated collective phonon modes and with classical simulated annealing. We further probe the quench dynamics of the Ising model in a transverse field to demonstrate quantum sampling tasks. Our work paves the way for simulating classically intractable quantum dynamics and for running noisy intermediate-scale quantum algorithms7,8 using 2D ion trap quantum simulators.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental setup and 2D ion crystals.
Fig. 2: Spatial correlation patterns in quasi-adiabatically prepared ground states for N = 300 qubits.
Fig. 3: Quantum simulation of a frustrated Ising model.
Fig. 4: Quench dynamics and quantum sampling.

Similar content being viewed by others

Data availability

The data supporting this work are available at Figshare https://doi.org/10.6084/m9.figshare.25572603 (ref. 48).

Code availability

The codes supporting this work are available from the corresponding author upon request.

References

  1. DiVincenzo, D. P. The physical implementation of quantum computation. Fortschr. Phys. 48, 771–783 (2000).

    Article  Google Scholar 

  2. Zhang, J. et al. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 551, 601–604 (2017).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  3. Joshi, M. K. et al. Exploring large-scale entanglement in quantum simulation. Nature 624, 539–544 (2023).

  4. Li, B.-W. et al. Probing critical behavior of long-range transverse-field ising model through quantum Kibble-Zurek mechanism. PRX Quantum 4, 010302 (2023).

    Article  ADS  Google Scholar 

  5. Britton, J. W. et al. Engineered two-dimensional ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489–492 (2012).

    Article  ADS  CAS  PubMed  Google Scholar 

  6. Bohnet, J. G. et al. Quantum spin dynamics and entanglement generation with hundreds of trapped ions. Science 352, 1297–1301 (2016).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  7. Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153–185 (2014).

    Article  ADS  Google Scholar 

  8. Bharti, K. et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004 (2022).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  9. Ebadi, S. et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  10. Kim, Y. et al. Evidence for the utility of quantum computing before fault tolerance. Nature 618, 500–505 (2023).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  11. Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).

    Article  ADS  CAS  PubMed  Google Scholar 

  12. Zhong, H.-S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  13. Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  14. Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  15. Hauke, P., Katzgraber, H. G., Lechner, W., Nishimori, H. & Oliver, W. D. Perspectives of quantum annealing: methods and implementations. Rep. Prog. Phys. 83, 054401 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  16. Cerezo, M. et al. Variational quantum algorithms. Nature Rev. Phys. 3, 625–644 (2021).

    Article  Google Scholar 

  17. Szymanski, B. et al. Large two dimensional Coulomb crystals in a radio frequency surface ion trap. Appl. Phys. Lett. 100, 171110 (2012).

    Article  ADS  Google Scholar 

  18. Xie, Y. et al. An open-endcap blade trap for radial-2d ion crystals. Quantum Sci. Technol. 6, 044009 (2021).

    Article  ADS  Google Scholar 

  19. Kato, A. et al. Two-tone doppler cooling of radial two-dimensional crystals in a radio-frequency ion trap. Phys. Rev. A 105, 023101 (2022).

    Article  ADS  CAS  Google Scholar 

  20. Kiesenhofer, D. et al. Controlling two-dimensional coulomb crystals of more than 100 ions in a monolithic radio-frequency trap. PRX Quantum 4, 020317 (2023).

    Article  ADS  Google Scholar 

  21. Qiao, M. et al. Tunable quantum simulation of spin models with a two-dimensional ion crystal. Nat. Phys. 20, 623–630 (2024).

  22. Sterling, R. C. et al. Fabrication and operation of a two-dimensional ion-trap lattice on a high-voltage microchip. Nature Commun. 5, 3637 (2014).

    Article  ADS  CAS  Google Scholar 

  23. Kiefer, P. et al. Floquet-engineered vibrational dynamics in a two-dimensional array of trapped ions. Phys. Rev. Lett. 123, 213605 (2019).

    Article  ADS  CAS  PubMed  Google Scholar 

  24. Holz, P. C. et al. 2D linear trap array for quantum information processing. Adv. Quantum Technol. 3, 2000031 (2020).

    Article  CAS  Google Scholar 

  25. Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl Inst. Stand. Technol. 103, 259 (1998).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  26. Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).

    Article  ADS  CAS  PubMed  Google Scholar 

  27. Amini, J. M. et al. Toward scalable ion traps for quantum information processing. New J. Phys. 12, 033031 (2010).

    Article  ADS  Google Scholar 

  28. Shu, G. et al. Heating rates and ion-motion control in a \({\mathsf{Y}}\)-junction surface-electrode trap. Phys. Rev. A 89, 062308 (2014).

    Article  ADS  Google Scholar 

  29. Burton, W. C. et al. Transport of multispecies ion crystals through a junction in a radio-frequency paul trap. Phys. Rev. Lett. 130, 173202 (2023).

    Article  ADS  CAS  PubMed  Google Scholar 

  30. Li, B.-W. et al. Observation of non-markovian spin dynamics in a Jaynes-Cummings-Hubbard model using a trapped-ion quantum simulator. Phys. Rev. Lett. 129, 140501 (2022).

    Article  ADS  CAS  PubMed  Google Scholar 

  31. Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974 (1999).

    Article  ADS  Google Scholar 

  32. Kim, K. et al. Entanglement and tunable spin–spin couplings between trapped ions using multiple transverse modes. Phys. Rev. Lett. 103, 120502 (2009).

    Article  ADS  CAS  PubMed  Google Scholar 

  33. Baldwin, C. H. et al. High-fidelity light-shift gate for clock-state qubits. Phys. Rev. A 103, 012603 (2021).

    Article  ADS  CAS  Google Scholar 

  34. Roman, C., Ransford, A., Ip, M. & Campbell, W. C. Coherent control for qubit state readout. New J. Phys. 22, 073038 (2020).

    Article  ADS  Google Scholar 

  35. Edmunds, C. L. et al. Scalable hyperfine qubit state detection via electron shelving in the 2D5/2 and 2F7/2 manifolds in 171yb+. Phys. Rev. A 104, 012606 (2021).

    Article  ADS  CAS  Google Scholar 

  36. Yang, H.-X. et al. Realizing coherently convertible dual-type qubits with the same ion species. Nature Phys. 18, 1058–1061 (2022).

    Article  ADS  CAS  Google Scholar 

  37. Smith, A., Kim, M. S., Pollmann, F. & Knolle, J. Simulating quantum many-body dynamics on a current digital quantum computer. npj Quantum Inform. 5, 106 (2019).

    Article  ADS  Google Scholar 

  38. Aloisio, I., White, G., Hill, C. & Modi, K. Sampling complexity of open quantum systems. PRX Quantum 4, 020310 (2023).

    Article  ADS  Google Scholar 

  39. Wang, S.-T. & Duan, L.-M. Certification of boson sampling devices with coarse-grained measurements. Preprint at https://arxiv.org/abs/1601.02627 (2016).

  40. Mao, Z.-C. et al. Experimental realization of multi-ion sympathetic cooling on a trapped ion crystal. Phys. Rev. Lett. 127, 143201 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  41. Korenblit, S. et al. Quantum simulation of spin models on an arbitrary lattice with trapped ions. New J. Phys. 14, 095024 (2012).

    Article  ADS  Google Scholar 

  42. Wu, Q., Shi, Y. & Zhang, J. Qubits on programmable geometries with a trapped-ion quantum processor. Preprint at https://arxiv.org/abs/2308.10179 (2023).

  43. Shapira, Y., Manovitz, T., Akerman, N., Stern, A. & Ozeri, R. Quantum simulations of interacting systems with broken time-reversal symmetry. Phys. Rev. X 13, 021021 (2023).

    CAS  Google Scholar 

  44. Pu, Y. et al. Experimental realization of a multiplexed quantum memory with 225 individually accessible memory cells. Nature Commun. 8, 15359 (2017).

    Article  ADS  CAS  Google Scholar 

  45. Wang, Y. et al. High-fidelity two-qubit gates using a microelectromechanical-system-based beam steering system for individual qubit addressing. Phys. Rev. Lett. 125, 150505 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  46. Wang, S.-T., Shen, C. & Duan, L.-M. Quantum computation under micromotion in a planar ion crystal. Sci. Rep. 5, 8555 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  47. Wu, Y.-K., Liu, Z.-D., Zhao, W.-D. & Duan, L.-M. High-fidelity entangling gates in a three-dimensional ion crystal under micromotion. Phys. Rev. A 103, 022419 (2021).

    Article  ADS  CAS  Google Scholar 

  48. Guo, S.-A. et al. Data used in ”A Site-Resolved 2D Quantum Simulator with Hundreds of Trapped Ions”. figshare https://doi.org/10.6084/m9.figshare.25572603 (2024).

Download references

Acknowledgements

This work was supported by the Innovation Programme for Quantum Science and Technology (grant nos. 2021ZD0301601 and 2021ZD0301605), the Tsinghua University Initiative Scientific Research Programme and the Ministry of Education of China. L.-M.D. acknowledges in addition support from the New Cornerstone Science Foundation through the New Cornerstone Investigator Programme. Y.-K.W. acknowledges in addition support from the Tsinghua University Dushi Programme and the Tsinghua University Start-up Fund.

Author information

Authors and Affiliations

  1. Center for Quantum Information, Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing, P.R. China

    S.-A. Guo, Y.-K. Wu, J. Ye, L. Zhang, Y. Wang, R.-Y. Yan, Y.-J. Yi, Y.-L. Xu, Y.-H. Hou, Y.-Z. Xu, C. Zhang, B.-X. Qi, Z.-C. Zhou, L. He & L.-M. Duan

  2. Hefei National Laboratory, Hefei, P.R. China

    Y.-K. Wu, Z.-C. Zhou, L. He & L.-M. Duan

  3. HYQ Co., Ltd, Beijing, P.R. China

    W.-Q. Lian, R. Yao, Y. Wang, B.-W. Li & W.-X. Guo

  4. New Cornerstone Science Laboratory, Beijing, P.R. China

    L.-M. Duan

Authors
  1. S.-A. Guo
    View author publications

    Search author on:PubMed Google Scholar

  2. Y.-K. Wu
    View author publications

    Search author on:PubMed Google Scholar

  3. J. Ye
    View author publications

    Search author on:PubMed Google Scholar

  4. L. Zhang
    View author publications

    Search author on:PubMed Google Scholar

  5. W.-Q. Lian
    View author publications

    Search author on:PubMed Google Scholar

  6. R. Yao
    View author publications

    Search author on:PubMed Google Scholar

  7. Y. Wang
    View author publications

    Search author on:PubMed Google Scholar

  8. R.-Y. Yan
    View author publications

    Search author on:PubMed Google Scholar

  9. Y.-J. Yi
    View author publications

    Search author on:PubMed Google Scholar

  10. Y.-L. Xu
    View author publications

    Search author on:PubMed Google Scholar

  11. B.-W. Li
    View author publications

    Search author on:PubMed Google Scholar

  12. Y.-H. Hou
    View author publications

    Search author on:PubMed Google Scholar

  13. Y.-Z. Xu
    View author publications

    Search author on:PubMed Google Scholar

  14. W.-X. Guo
    View author publications

    Search author on:PubMed Google Scholar

  15. C. Zhang
    View author publications

    Search author on:PubMed Google Scholar

  16. B.-X. Qi
    View author publications

    Search author on:PubMed Google Scholar

  17. Z.-C. Zhou
    View author publications

    Search author on:PubMed Google Scholar

  18. L. He
    View author publications

    Search author on:PubMed Google Scholar

  19. L.-M. Duan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

L.-M.D. proposed and supervised the project. S.-A.G., J.Y., L.Z., W.-Q.L., R.Y., Y.W., R.-Y.Y., Y.-J.Y., Y.-L.X., B.-W.L., Y.-H.H., Y.-Z.X., W.-X.G., C.Z., B.-X.Q., Z.-C.Z. and L.H. carried out the experiment. S.-A.G., Y.-K.W. and J.Y. analysed the data and did the associated theory. Y.-K.W., S.-A.G., and L.-M.D. wrote the manuscript.

Corresponding author

Correspondence to L.-M. Duan.

Ethics declarations

Competing interests

W.-Q.L., R.Y., Y.W., B.-W.L. and W.-X.G. are affiliated with HYQ Co. Y.-K.W., W.-Q.L., R.Y., Y.W., B.-W.L., Y.-Z.X., W.-X.G., B.-X.Q., Z.-C.Z., L.H. and L.-M.D. hold shares with HYQ Co. The other authors declare no competing interests.

Peer review

Peer review information

Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Sections 1–5 including Figs. 1–9 and references.

Peer Review File

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, SA., Wu, YK., Ye, J. et al. A site-resolved two-dimensional quantum simulator with hundreds of trapped ions. Nature 630, 613–618 (2024). https://doi.org/10.1038/s41586-024-07459-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-024-07459-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing