Abstract
One-dimensional (1D) interacting electrons are often described as a Luttinger liquid1,2,3,4 having properties that are intrinsically different from those of Fermi liquids in higher dimensions5,6. In materials systems, 1D electrons exhibit exotic quantum phenomena that can be tuned by both intra- and inter-1D-chain electronic interactions, but their experimental characterization can be challenging. Here we demonstrate that layer-stacking domain walls (DWs) in van der Waals heterostructures form a broadly tunable Luttinger liquid system, including both isolated and coupled arrays. We have imaged the evolution of DW Luttinger liquids under different interaction regimes tuned by electron density using scanning tunnelling microscopy. Single DWs at low carrier density are highly susceptible to Wigner crystallization consistent with a spin-incoherent Luttinger liquid, whereas at intermediate densities dimerized Wigner crystals form because of an enhanced magneto-elastic coupling. Periodic arrays of DWs exhibit an interplay between intra- and inter-chain interactions that gives rise to new quantum phases. At low electron densities, inter-chain interactions are dominant and induce a 2D electron crystal composed of phased-locked 1D Wigner crystal in a staggered configuration. Increased electron density causes intra-chain fluctuation potentials to dominate, leading to an electronic smectic liquid crystal phase in which electrons are ordered with algebraical correlation decay along the chain direction but disordered between chains. Our work shows that layer-stacking DWs in 2D heterostructures provides opportunities to explore Luttinger liquid physics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data supporting the findings of this study can be found at GitHub (https://github.com/HongyuanLiCMP/Imaging-Tunable-Luttinger-Liquid-Systems-in-van-der-Waals-Heterostructures) and are also available from the corresponding authors upon reasonable request.
References
Imambekov, A., Schmidt, T. L. & Glazman, L. I. One-dimensional quantum liquids: beyond the Luttinger liquid paradigm. Rev. Mod. Phys. 84, 1253–1306 (2012).
Haldane, F. D. M. Effective harmonic-fluid approach to low-energy properties of one-dimensional quantum fluids. Phys. Rev. Lett. 47, 1840–1843 (1981).
Haldane, F. D. M. ‘Luttinger liquid theory’ of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C Solid State Phys. 14, 2585–2610 (1981).
Voit, J. One-dimensional Fermi liquids. Rep. Prog. Phys. 58, 977–1116 (1995).
Baym, G. & Pethick, C. Landau Fermi-Liquid Theory: Concepts and Applications (Wiley, 2008).
Nozieres, P. Theory of Interacting Fermi Systems (CRC Press, 2018).
Fiete, G. A., Le Hur, K. & Balents, L. Coulomb drag between two spin-incoherent Luttinger liquids. Phys. Rev. B 73, 165104 (2006).
Fiete, G. A. Colloquium: the spin-incoherent Luttinger liquid. Rev. Mod. Phys. 79, 801–820 (2007).
Moskovtsev, K. & Dykman, M. Mobility of a spatially modulated electron liquid on the helium surface. Phys. Rev. B 101, 245435 (2020).
Reichhardt, C. & Reichhardt, C. J. O. Collective dynamics and defect generation for Wigner crystal ratchets. Phys. Rev. B 108, 155131 (2023)
Teo, J. C. Y. & Kane, C. L. From Luttinger liquid to non-Abelian quantum Hall states. Phys. Rev. B 89, 085101 (2014).
Mukhopadhyay, R., Kane, C. L. & Lubensky, T. C. Sliding Luttinger liquid phases. Phys. Rev. B 64, 045120 (2001).
Ohtsubo, Y. et al. Surface Tomonaga-Luttinger-liquid state on Bi/InSb(001). Phys. Rev. Lett. 115, 256404 (2015).
Jompol, Y. et al. Probing spin-charge separation in a Tomonaga-Luttinger liquid. Science 325, 597–601 (2009).
Shapir, I. et al. Imaging the electronic Wigner crystal in one dimension. Science 364, 870–875 (2019).
Bockrath, M. et al. Luttinger-liquid behaviour in carbon nanotubes. Nature 397, 598–601 (1999).
Ishii, H. et al. Direct observation of Tomonaga–Luttinger-liquid state in carbon nanotubes at low temperatures. Nature 426, 540–544 (2003).
Lee, J. et al. Real space imaging of one-dimensional standing waves: direct evidence for a Luttinger liquid. Phys. Rev. Lett. 93, 166403 (2004).
Chang, A. Chiral Luttinger liquids at the fractional quantum Hall edge. Rev. Mod. Phys. 75, 1449–1505 (2003).
Wen, X.-G. Chiral Luttinger liquid and the edge excitations in the fractional quantum Hall states. Phys. Rev. B 41, 12838–12844 (1990).
Stühler, R. et al. Tomonaga–Luttinger liquid in the edge channels of a quantum spin Hall insulator. Nat. Phys. 16, 47–51 (2020).
Li, T. et al. Observation of a helical Luttinger liquid in InAs/GaSb quantum spin Hall edges. Phys. Rev. Lett. 115, 136804 (2015).
Zhu, T. et al. Imaging gate-tunable Tomonaga–Luttinger liquids in 1H-MoSe2 mirror twin boundaries. Nat. Mater. 21, 748–753 (2022).
Jolie, W. et al. Tomonaga-Luttinger liquid in a box: electrons confined within MoS2 mirror-twin boundaries. Phys. Rev. X 9, 011055 (2019).
Deshpande, V. V. & Bockrath, M. The one-dimensional Wigner crystal in carbon nanotubes. Nat. Phys. 4, 314–318 (2008).
Emery, V. J., Kivelson, S. A. & Zachar, O. Spin-gap proximity effect mechanism of high-temperature superconductivity. Phys. Rev. B 56, 6120–6147 (1997).
Wang, P. et al. One-dimensional Luttinger liquids in a two-dimensional moiré lattice. Nature 605, 57–62 (2022).
Li, H. et al. Imaging moiré flat bands in three-dimensional reconstructed WSe2/WS2 superlattices. Nat. Mater. 20, 945–950 (2021).
Schweizer, P., Dolle, C. & Spiecker, E. In situ manipulation and switching of dislocations in bilayer graphene. Sci. Adv. 4, eaat4712 (2018).
Alden, J. S. et al. Strain solitons and topological defects in bilayer graphene. Proc. Natl Acad. Sci. USA 110, 11256–11260 (2013).
Rupp, A. et al. Imaging lattice reconstruction in homobilayers and heterobilayers of transition metal dichalcogenides. 2D Mater. 10, 045028 (2023).
Kim, J. H. et al. Interface‐driven partial dislocation formation in 2D heterostructures. Adv. Mater. 31, 1807486 (2019).
Shabani, S. et al. Deep moiré potentials in twisted transition metal dichalcogenide bilayers. Nat. Phys. 17, 720–725 (2021).
Edelberg, D., Kumar, H., Shenoy, V., Ochoa, H. & Pasupathy, A. N. Tunable strain soliton networks confine electrons in van der Waals materials. Nat. Phys. 16, 1097–1102 (2020).
Weston, A. et al. Atomic reconstruction in twisted bilayers of transition metal dichalcogenides. Nat. Nanotechnol. 15, 592–597 (2020).
Li, H. et al. Wigner molecular crystals from multi-electron moiré artificial atoms. Preprint at arxiv.org/abs/2312.07607 (2023).
Vu, D. & Sarma, S. D. One-dimensional few-electron effective Wigner crystal in quantum and classical regimes. Phys. Rev. B 101, 125113 (2020).
Drummond, N. & Needs, R. Phase diagram of the low-density two-dimensional homogeneous electron gas. Phys. Rev. Lett. 102, 126402 (2009).
Ceperley, D. Ground state of the fermion one-component plasma: a Monte Carlo study in two and three dimensions. Phys. Rev. B 18, 3126–3138 (1978).
Tanatar, B. & Ceperley, D. M. Ground state of the two-dimensional electron gas. Phys. Rev. B 39, 5005–5016 (1989).
Piro, O. E., Echeverría, G. A. & Cukiernik, F. D. Crystallography and the liquid crystal phase: a new approach to structural studies on a thermo-tropic smectic Schiff base. Crystallogr. Rev. 24, 3–21 (2018).
de Vries, A. A structural classification of smectic liquid crystals. Mol. Cryst. Liq. Cryst. 63, 215–229 (1981).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Farahi, G. et al. Broken symmetries and excitation spectra of interacting electrons in partially filled Landau levels. Nat. Phys. 19, 1482–1488 (2023).
Bray, J. W. et al. Observation of a spin-Peierls transition in a Heisenberg antiferromagnetic linear-chain system. Phys. Rev. Lett. 35, 744–747 (1975).
Cross, M. C. & Fisher, D. S. A new theory of the spin-Peierls transition with special relevance to the experiments on TTFCuBDT. Phys. Rev. B 19, 402–419 (1979).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Acknowledgements
This work was primarily funded by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division under contract no. DE-AC02-05-CH11231 within the van der Waals heterostructure programme KCFW16 (device fabrication, STM spectroscopy, theoretical analyses and computations). Support was also provided by the National Science Foundation Award DMR-2221750 (surface preparation). This research used the Lawrencium computational cluster provided by the Lawrence Berkeley National Laboratory (supported by the US Department of Energy, Office of Basic Energy Sciences, under contract no. DE-AC02-05-CH11231). S.T. acknowledges primary support from the US Department of Energy SC0020653 (materials synthesis), NSF CMMI1825594 (NMR and TEM studies on crystals), NSF DMR-1955889 (magnetic measurements on crystals), NSF ECCS2052527 (bulk electrical tests), DMR 2111812 and CMMI 2129412 (optical tests on bulk crystals). K.W. and T.T. acknowledge support from the JSPS KAKENHI (grant nos. 21H05233 and 23H02052) and the World Premier International Research Center Initiative (WPI), MEXT, Japan. H.L. acknowledges support from Kavli Energy Nano Sciences Institute graduate student fellowship. We acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing high-performance computing resources. This research also used resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy, Office of Science User Facility, located at Lawrence Berkeley National Laboratory, operated under contract no. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
H.L., M.P.Z., M.F.C. and F.W. conceived the project. H.L., Z.X., J.N. and S.L. fabricated the WS2 heterostructure device. H.L. and Z.X. performed the STM/STS measurement of the WS2 device. T.W. and M.P.Z. performed the DMRG calculations of the 1D interacting electrons. M.H.N., W.K. and S.G.L. performed the ab initio calculations of the DW structures. Z.G. and Z.H. performed the measurement of the QPI in bilayer MoSe2. H.L., Z.X., A.Z., M.F.C. and F.W. discussed the experimental design and analysed the experimental data. Y.O., R.B. and S.T. grew the WS2 crystals. K.W. and T.T. grew the hBN single crystal. All authors discussed the results and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Wouter Jolie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
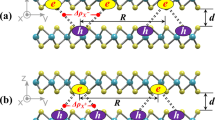
Extended Data Fig. 1 Sketch of the atomic structure for a shear-type stacking DW.
The left and right regions are AB stacked while the center shows a vertically aligned DW. The positions of W atoms in the bottom layer (orange dots) and S atoms in the top layer (blue dots) are highlighted along a linecut across the DW. For shear-type DWs, the two AB stacking regions have an interlayer unit-vector shift parallel to the DW.
Extended Data Fig. 2 Conduction band edge tunnel current measurement.
a. Schematic energy diagram for the conduction band edge (CBE) tunnel current measurement of electron-doped WS2. The WS2 chemical potential \({\mu }_{W{S}_{2}}\) lies above the CBE. When the tip chemical potential \({\mu }_{{tip}}\) (controlled by Vbias) is the aligned within the band gap of the WS2, the tunnel current arises from the doped electrons at the conduction band edge. b,c. Tunnel current I-V characteristics as a function of VBG measured at the DW center for electron-doped WS2 with (b) a large (Vbias = −3.30 V, Isp = 20 pA, htip = −50 pm) and (c) small (Vbias = −2.70 V, Isp = 20 pA, htip = −100 pm) tip-sample separation. The current is plotted on a log scale with the positive and negative branches using different colormaps. The CBE and valence band edge (VBE) are marked with white dashed lines. For small tip-sample separation a negative CBE tunnel current can be seen in the WS2 gap.
Extended Data Fig. 3 Analysis of the Wigner-Friedel crossover.
a. Calculated charge phonon energy \(\hbar {\omega }_{0}\) and exchange interaction energy \({E}_{J}\) as a function of 1D chain electron density. The experimental temperature energy scale is labeled with a green dashed line. b. Schematic illustration of 1D electron chain with decreasing interaction strength (from bottom to top) shows three regimes: Wigner crystal, dimerized crystal, and Friedel oscillation. c. DMRG calculation of the charge density \(n(x)\) and entanglement entropy \({S}_{{EE}}\) across each site of 1D electron chain for n = 0.3 nm−1 (see SI section 6 for details). SEE reflects the degree of entanglement (and therefore singlet formation) between neighboring electrons in a dimerized Wigner crystal. Vertical lines label the boundary (solid) and center (dashed) of singlet pairs.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, H., Xiang, Z., Wang, T. et al. Imaging tunable Luttinger liquid systems in van der Waals heterostructures. Nature 631, 765–770 (2024). https://doi.org/10.1038/s41586-024-07596-6
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-07596-6
This article is cited by
-
Platforms for the realization and characterization of Tomonaga–Luttinger liquids
Nature Reviews Physics (2025)
-
Transferable dispersion-aware machine learning interatomic potentials for multilayer transition metal dichalcogenide heterostructures
npj Computational Materials (2025)