Abstract
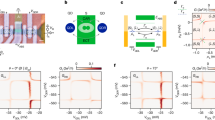
A chain of quantum dots (QDs) in semiconductor–superconductor hybrid systems can form an artificial Kitaev chain hosting Majorana bound states (MBSs)1,2,3. These zero-energy states are expected to be localized on the edges of the chain4, at the outermost QDs. The remaining QDs, comprising the bulk, are predicted to host an excitation gap that protects the MBSs at the edges from local on-site perturbations. Here we demonstrate this connection between the bulk and edges in a minimal system, by engineering a three-site Kitaev chain in a two-dimensional electron gas. Through direct tunnelling spectroscopy on each site, we show that the appearance of stable zero-bias conductance peaks at the outer QDs is correlated with the presence of an excitation gap in the middle QD. Furthermore, we show that this gap can be controlled by applying a superconducting phase difference between the two hybrid segments and that the MBSs are robust only when the excitation gap is present. We find a close agreement between experiments and the original Kitaev model, thus confirming key predictions for MBSs in a three-site chain.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All raw data obtained in this study and the scripts to produce the figures are available at Zenodo56.
References
Sau, J. D. & Sarma, S. D. Realizing a robust practical Majorana chain in a quantum-dot-superconductor linear array. Nat. Commun. 3, 964 (2012).
Leijnse, M. & Flensberg, K. Parity qubits and poor man’s Majorana bound states in double quantum dots. Phys. Rev. B 86, 134528 (2012).
Fulga, I. C., Haim, A., Akhmerov, A. R. & Oreg, Y. Adaptive tuning of Majorana fermions in a quantum dot chain. New J. Phys. 15, 045020 (2013).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 44, 131 (2001).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Lutchyn, R. M., Sau, J. D. & Sarma, S. D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & Oppen, F.von Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Halperin, B. I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982).
Wen, X.-G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 44, 405–473 (1995).
Prada, E. et al. From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires. Nat. Rev. Phys. 2, 575–594 (2020).
Liu, C.-X., Sau, J. D., Stanescu, T. D. & Sarma, S. D. Andreev bound states versus Majorana bound states in quantum dot-nanowire-superconductor hybrid structures: Trivial versus topological zero-bias conductance peaks. Phys. Rev. B 96, 075161 (2017).
Reeg, C., Dmytruk, O., Chevallier, D., Loss, D. & Klinovaja, J. Zero-energy Andreev bound states from quantum dots in proximitized Rashba nanowires. Phys. Rev. B 98, 245407 (2018).
Vuik, A., Nijholt, B., Akhmerov, A. R. & Wimmer, M. Reproducing topological properties with quasi-Majorana states. SciPost Phys. 7, 061 (2019).
Pan, H. & Sarma, S. D. Physical mechanisms for zero-bias conductance peaks in Majorana nanowires. Phys. Rev. Res. 2, 013377 (2020).
Sarma, S. D. & Pan, H. Disorder-induced zero-bias peaks in Majorana nanowires. Phys. Rev. B 103, 195158 (2021).
Kouwenhoven, L. Perspective on Majorana bound-states in hybrid superconductor-semiconductor nanowires. Mod. Phys. Lett. B 39, 2540002 (2025).
Li, J. et al. Topological superconductivity induced by ferromagnetic metal chains. Phys. Rev. B 90, 235433 (2014).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Dvir, T. et al. Realization of a minimal Kitaev chain in coupled quantum dots. Nature 614, 445–450 (2023).
Haaf, S. L. D. et al. A two-site Kitaev chain in a two-dimensional electron gas. Nature 630, 329–334 (2024).
Bordin, A. et al. Enhanced Majorana stability in a three-site Kitaev chain. Nat. Nanotechnol. https://doi.org/10.1038/s41565-025-01894-4 (2025).
Liu, C.-X., Wang, G., Dvir, T. & Wimmer, M. Tunable superconducting coupling of quantum dots via Andreev bound states in semiconductor-superconductor nanowires. Phys. Rev. Lett. 129, 267701 (2022).
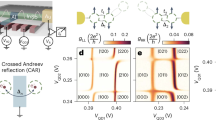
Bordin, A. et al. Tunable crossed Andreev reflection and elastic cotunneling in hybrid nanowires. Phys. Rev. X 13, 031031 (2023).
Bordin, A. et al. Crossed andreev reflection and elastic cotunneling in three quantum dots coupled by superconductors. Phys. Rev. Lett. 132, 056602 (2024).
Liu, Z.-H., Zeng, C. & Xu, H. Q. Coupling of quantum-dot states via elastic cotunneling and crossed Andreev reflection in a minimal Kitaev chain. Phys. Rev. B 110, 115302 (2024).
Wang, G. et al. Singlet and triplet Cooper pair splitting in hybrid superconducting nanowires. Nature 612, 448–453 (2022).
Tsintzis, A., Souto, R. S. & Leijnse, M. Creating and detecting poor man’s Majorana bound states in interacting quantum dots. Phys. Rev. B 106, L201404 (2022).
Luethi, M., Legg, H. F., Loss, D. & Klinovaja, J. From perfect to imperfect poor man’s majoranas in minimal kitaev chains. Phys. Rev. B 110, 245412 (2024).
Liu, C.-X. et al. Scaling up a sign-ordered Kitaev chain without magnetic flux control. Phys. Rev. Res. 7, L012045 (2025).
Wang, Q. et al. Triplet correlations in Cooper pair splitters realized in a two-dimensional electron gas. Nat. Commun. 14, 4876 (2023).
Zatelli, F. et al. Robust poor man’s Majorana zero modes using Yu-Shiba-Rusinov states. Nat. Commun. 15, 7933 (2024).
Bozkurt, A. M. et al. Interaction-induced strong zero modes in short quantum dot chains with time-reversal symmetry. Preprint at arxiv.org/abs/2405.14940 (2024).
Liu, C.-X. et al. Enhancing the excitation gap of a quantum-dot-based Kitaev chain. Commun. Phys. 7, 235 (2024).
Pandey, B., Gupta, G. K., Alvarez, G., Okamoto, S. & Dagotto, E. Diabatic error and propagation of Majorana zero modes in interacting quantum dots systems. Preprint at arxiv.org/abs/2501.06288 (2025).
Pandey, B., Okamoto, S. & Dagotto, E. Nontrivial fusion of Majorana zero modes in interacting quantum-dot arrays. Phys. Rev. Res. 6, 033314 (2024).
Pandey, B., Kaushal, N., Alvarez, G. & Dagotto, E. Majorana zero modes in Y-shape interacting Kitaev wires. NPJ Quantum Mater. 8, 51 (2023).
Leumer, N., Marganska, M., Muralidharan, B. & Grifoni, M. Exact eigenvectors and eigenvalues of the finite Kitaev chain and its topological properties. J. Phys. Condens. Matter 32, 445502 (2020).
Ezawa, M. Even-odd effect on robustness of Majorana edge states in short Kitaev chains. Phys. Rev. B 109, L161404 (2024).
Luethi, M., Legg, H. F., Loss, D. & Klinovaja, J. The fate of poor man’s Majoranas in the long Kitaev chain limit. Preprint at arxiv.org/abs/2408.10030 (2025).
Svensson, V. & Leijnse, M. Quantum dot based Kitaev chains: Majorana quality measures and scaling with increasing chain length. Phys. Rev. B 110, 155436 (2024).
Alicea, J., Oreg, Y., Refael, G., Oppen, F. & Fisher, M. P. A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 7, 412–417 (2011).
Boross, P. & Pályi, A. Braiding-based quantum control of a Majorana qubit built from quantum dots. Phys. Rev. B 109, 125410 (2024).
Tsintzis, A., Souto, R. S., Flensberg, K., Danon, J. & Leijnse, M. Majorana qubits and non-abelian physics in quantum dot–based minimal Kitaev chains. PRX Quantum 5, 010323 (2024).
Liu, C.-X., Pan, H., Setiawan, F., Wimmer, M. & Sau, J. D. Fusion protocol for Majorana modes in coupled quantum dots. Phys. Rev. B 108, 085437 (2023).
Pan, H., Sarma, S. D. & Liu, C.-X. Rabi and Ramsey oscillations of a Majorana qubit in a quantum dot-superconductor array. Phys. Rev. B 111, 075416 (2025).
Moehle, C. M. et al. InSbAs two-dimensional electron gases as a platform for topological superconductivity. Nano Lett. 21, 9990–9996 (2021).
Martinez, E.A. et al. Measurement circuit effects in three-terminal electrical transport measurements. Preprint at arxiv.org/abs/2104.02671 (2021).
Vigneau, F. et al. Probing quantum devices with radio-frequency reflectometry. Appl. Phys. Rev. 10, 021305 (2023).
Kulesh, I. et al. A flux-controlled two-site Kitaev chain. Preprint at arxiv.org/abs/2501.15912 (2025).
Hornibrook, J. M. et al. Frequency multiplexing for readout of spin qubits. Appl. Phys. Lett. 104, 103108 (2014).
Pavešič, L., Aguado, R. & Žitko, R. Strong-coupling theory of quantum-dot Josephson junctions: Role of a residual quasiparticle. Phys. Rev. B 109, 125131 (2024).
Beenakker, C. W. J. Theory of Coulomb-blockade oscillations in the conductance of a quantum dot. Phys. Rev. B 44, 1646–1656 (1991).
Haaf, S. L. D. Data and code for “Edge and bulk states in a three-site Kitaev chain”. Zenodo https://doi.org/10.5281/zenodo.15020006 (2025).
Jellinggaard, A., Grove-Rasmussen, K., Madsen, M. H. & Nygård, J. Tuning Yu-Shiba-Rusinov states in a quantum dot. Phys. Rev. B 94, 064520 (2016).
Acknowledgements
We thank O. W. B. Benningshof and J. D. Mensingh for technical assistance with the cryogenic electronics. We thank L. Vandersypen, R. Aguado, R. Seoane, M. Leijnse, G. Wang, A. M. Bozkurt, N. van Loo, G. P. Mazur, F. Zatelli and L. Kouwenhoven for providing valuable inputs on the paper. The research at Delft was supported by the Dutch National Science Foundation (NWO), Microsoft Corporation Station Q and a grant from the Top Consortium for Knowledge and Innovation (TKI) program. S.G. and M.W. acknowledge financial support from the Horizon Europe Framework Program of the European Commission through the European Innovation Council Pathfinder grant no. 101115315 (QuKiT).
Author information
Authors and Affiliations
Contributions
Q.W. fabricated the device, with input from S.L.D.t.H and I.K.; Y.Z. and I.K. fabricated the resonator circuits. C.G.P. and I.K. designed the measurement set-up. Measurements were performed by S.L.D.t.H, V.P.M.S., Y.Z. and A.B.; C.-X.L. and M.W. provided the theoretical analysis, with C.-X.L. carrying out the analytical calculations and the numerical simulations. MBE growth of the semiconductor heterostructures and the characterization of the materials were performed by D.X. and C.T. under the supervision of M.J.M. The paper was written by S.L.D.t.H. and S.G., with input from all co-authors. S.G. supervised the experimental work in Delft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Device description and characterisation of hybrid sections.
a. Zoomed out SEMs of copies of the measured device obtained after deposition of Ohmic contacts, showing the full structure of the superconducting loop. b. Close-up SEM of the finished device, including the full circuit diagram. Bottom left in-set shows a cross-sectional schematic of the device along the channel, adapted from Q.W. (manuscript in preparation), to visualise the order of the three gate layers. Resonators are formed by inductors in combination with a parasitic capacitances to ground, which allows for fast radio-frequency (RF) measurements, used in this work for tuning and characterisation of the system. Voltage sources and current meters are attached to each lead via ≈ 5 kΩ resistors, acting as bias tees, used to obtain the conductance measurements in the main text. Sub-figures (c-h.) show characterisations of the three possible hybrid configurations, after a 1-D channel is formed with the large depletion gates. Schematics on the right display the activated tunneling gates and relevant Ohmic contacts for each row. c. RF-spectroscopy of the Josephson junction formed by the two superconducting fingers at the ends of the loop, as a function of the magnetic field Bz perpendicular to the loop. d Measured current IR with VR = 100 μV, in a wider range of Bz. Fitting the oscillations with a periodic Gaussian function provides an estimate for the flux periodicity (28 μT). e Tunneling spectroscopy of the left SC finger in isolation, as a function of \({V}_{{\rm{ABS}}}^{{\rm{(1)}}}\) applied to the gate covering the left hybrid region. f. Line-trace from (e) at \({V}_{{\rm{ABS}}}^{{\rm{(1)}}}\) = −100 mV, to show the presence of a sub-gap state in the left hybrid. g. Tunneling spectroscopy of the right SC finger in isolation, as a function of the gate covering the right hybrid region (\({V}_{{\rm{ABS}}}^{{\rm{(2)}}}\)). h. Line-trace from (g) at \({V}_{{\rm{ABS}}}^{{\rm{(2)}}}\) = 125 mV to show the presence of a sub-gap state in the right hybrid.
Extended Data Fig. 2 Quantum dot characterisations.
Results presented in the main text are obtained using a single orbital in each QD. Characterisation measurements of each QD is shown here. Left, middle and right columns pertain to the left, middle and right QD respectively. a-c. Coulomb diamonds measured at Bx = 0 mT. To achieve strong interdot coupling, barriers between QD and neighbouring regions are kept relatively open, such that a finite current can be observed within each Coulomb diamond. The outline roughly indicates the charging energies to be > 1 mV. d-f. RF-Spectroscopy of each QD in the same regime as (a-c), for a smaller range of applied voltage biases. In this strong coupling regime, so-called Yu-Shiba-Rusinov states form at sub-SC gap energy scales whose energies are non-linearly dependent on the plunger gate voltages57. g-i. Spectroscopy as a function of magnetic field Bx applied along the 1-D channel, with each plunger gate set close to the zero field charge degeneracy point based on (d-f). The slope of the splitting sub-gap states provides an estimate of the g-factors for these parameters to be 18.4, 14.8 and 13.7 respectively. j-m. Examples of QD-ABS charge stability diagrams, used to calibrate the interdot interactions following the procedure detailed in34,36. The discrepancies in the plunger gate voltages used for each orbital between (a-c) and (j-m) arise due to gate-jumps and cross-talk between neighbouring barrier gates.
Extended Data Fig. 3 QD stability.
a. Example of repeated RF-measurements of the middle QD resonances. The same measurement was repeated 100 times, once every second. The plot shows a stack of all repetitions. The resonances at −225 mV are observed to switch between two states during this time, which makes them unsuitable for slow DC measurements. b. In order to find a stable regime, we observe the effect of varying the barrier gates forming the QDs. Here, for example, the middle QD resonances are found to be more stable when the right barrier gate is tuned below −2.02 V. c. This becomes apparent when comparing repeated RF measurements for (i) unstable and (ii) stable regimes. d. In addition, charge-jumps in the gate voltages can affect the charge-stability diagrams. Panel (i) shows an example of a CSD for QDL and the left hybrid gate, where charge jumps occur in both \({V}_{{\rm{ABS}}}^{{\rm{1}}}\) and VQDL (indicated by the red arrows). By fine-tuning the barrier gates forming QDL, we can reach a state where these jumps are avoided in the region of interest, shown in panel (ii).
Extended Data Fig. 4 Conductance spectra of two-site QD pairs.
Studying CSDs for pairs of QDs provides information about the interdot couplings and allows one to reach the sweet spot conditions shown in Fig. 1c,d. In addition, finite bias conductance spectra at the two-site sweet spots should be obtained35 for all possible combinations of QD detunings. This is shown here for the charge configuration in Fig. 1. Adjacent schematics represent the configurations of the QDs and the parameters varied. Left column: tunneling spectroscopies of the left QD pair at a sweet spot (i.e. t1 = Δ1), with the right QD kept in Coulomb blockade. GLL and GMM are measured as a function of a. detuning VQDL, b. detuning VQDM, c. detuning both VQDL and VQDM simultaneously and d. Applying a magnetic field Bz perpendicular to the superconducting loop. Right column: tunneling spectroscopy of the right pair of QDs at a sweet spot (i.e. t2 = Δ2), with the left QD kept in Coulomb blockade. GMM and GRR are measured as a function of e. detuning VQDRf. detuning VQDM, g. detuning both VQDM and VQDR and h. Applying a magnetic field Bz perpendicular to the superconducting loop. It is important to note that (d) and (h) are obtained for the same configuration as the flux-dependence measurements in Fig. 2, with the only difference being that here the outer QD is kept in Coulomb blockade. The lack of response to Bz rules out more trivial origins of the flux dependence in Fig. 2, such as oscillations of the middle QDs electrochemical potential energy.
Extended Data Fig. 5 Fitting of conductance line-traces.
The measurements in Fig. 2 show a finite in-gap conductance in GMM when ϕΔ = 0. Possible origins for this include thermal broadening, and small deviations in the QD plunger gate voltages from being precisely at μi = 0. Here we address the former, by comparing the conductance bias-traces with the theoretically expected shapes in the small lead-QD coupling limit (Γ ≪ kBT) described in Methods. a. Repetitions of conductance spectra for GLL and GRR as a function of Bz, as shown in Fig. 2a. b. Line-cuts taken from the indicated position in (a), at Bz corresponding to ϕΔ = 0. GLL is fitted to Eq. (18) and GRR is fitted to Eq. (19), yielding estimates for t1 and t2. We find the conductances are well described by the temperature-limited fits and find both are described by the same broadening parameter (γ = 15.6). c. Repetition of conductance spectra for GMM as a function of Bz from Fig. 2a. d. Using the t1 and t2 values extracted in (b), we fit the indicated GMM line-cut from (c) to Eq. (20). In (i), γ is fixed to be the same value as extracted in (b), while in (ii) γ is included as fitting parameter. (iii) uses the same fitting as (ii), for a line-cut taken at a different 2π period as indicated in (c). The conductance is again well-described by the temperature-limited fit. A larger broadening parameter is however required, the origin of which is unclear and not captured by the numerical simulations. In (ii) and (iii) the measured conductance at VM = 0 is ≈ 3 mG0 larger than explained by the fits. From Eq. (16), this remainder would correspond to offsets in μL/μR on the order of ± 5 μeV. The plunger gate voltages are set with a resolution of 60 μV, which combined with a QD leverarm of ≈ 0.05 would translate to potential offsets on the order of 3 μeV in μL and μR. e-h. shows a repetition of the outlined procedure, for measurements using the charge configuration shown in Extended Data Fig. 11. A similar behaviour is observed.
Extended Data Fig. 6 Conductance spectra for ϕΔ between 0 and π.
In the main text, Fig. 3 shows measurements of conductance spectra at a three-site sweet spot, obtained at two Bz values corresponding to ϕΔ = 0 and ϕΔ = π. The ability to control the flux allows us to perform such measurements at any intermediate value of ϕΔ. a. RF-spectroscopy measurements of \({{\rm{S}}}_{21}^{{\rm{R}}}\) and corresponding numerical simulations, upon detuning VQDL, for seven values of Bz corresponding to ϕΔ = 0 and ϕΔ = π. The experimental evolution corresponds well to the numerical simulation at each stage. Recent work on a three-site Kitaev chain with two separately grounded SCs24 concludes that a small voltage difference between the SCs (on the order of μV) may give rise to rapid phase oscillations. Hence, it is assumed their (slow) measurements reflect an average over many periods of ϕΔ. b. Shows averaged RF-spectroscopy for 25 measurements in the same range as (a), and the corresponding numerically averaged simulation, finding good agreement with the reported behaviour in24.
Extended Data Fig. 7 Three-site conductance spectra for different QD detuning combinations.
In a three-site Kitaev chain, the ZBPs arising on the outer QDs are expected to persist when detuning either a single QD or pairs of QDs24. Figure 3 only demonstrates the response to detuning VQDL. Here, four other possible detuning combinations are highlighted, for the same device configuration. Accompanying numerical simulations use the same set of parameters as shown in the main text. Plunger gate voltages have been converted to chemical potential energies using the QD leverarms. a. and b. show repetitions of the conductance spectra shown in Fig. 3, where ϕΔ = 0 and ϕΔ = π respectively, including a comparison to the numerical simulation. Furthermore, we show the response at ϕΔ = 0 to c. Detuning VQDM (μM), d. detuning VQDR (μR), e. detuning both VQDL and VQDR and f. detuning all three QDs simultaneously. When ϕΔ = 0, the ZBP measured in GLL and GRR only splits from zero-energy when all three QDs are detuned.
Extended Data Fig. 8 Shifting the MBS wavefunction - comparison to analytical result.
At a three-site Kitaev chain sweet spot, with ϕΔ = 0, detuning either of the outer QDs shifts the MBS wave-function to the middle QD. In Methods, we derive that this reflects in the zero-bias conductance of each site and depends only on the coupling parameters t1/t2 (= Δ1/Δ2) (see Eqs. (16)). To do this analysis experimentally, first the chemical-potential energies μL, μR of QDL and QDR are measured as a function of a.VQDL and b.VQDR, by measuring each QD spectrum with the unused QDs in Coulomb blockade. With all parameters tuned to the sweet spot values, we detune VQDL around charge degeneracy and measure c. GLL and d. GMM, as shown in Fig. 3a. Additionally, we detune VQDR and measure e. GRR and f. GMM. As visualised in g. and h., these experiments result in the shifting of the MBS wave-function from the outer QD to the inner QD. In (c,d), the conductances measured at VL,VM = 0 depend only on μL and t1. Similarly for (e,f) they scale according to μR and t2. i. We extract GLL and GMM along VL,VM = 0 from (c) and (d) and convert VQDL to μL using (a). Fitting the analytical formulas shown in (g), with an additional scaling factor, an estimate for t1 of 17.6 μeV is obtained. This can be compared to the width of the excitation gap at μL = 0, which theory predicts to be 2t1. j. shows the line-trace, with the dashed lines indicating the expected location of the excited states based on the extraction in (i). k. We repeat this procedure for GRR and GMM along VR,VM = 0 from (e) and (f), converting VQDL to μR using (b). Now fitting the formulates shown in (h), we can estimate t2 of 23.7 μeV. l. This again agrees with the excitation gap at μR = 0.
Extended Data Fig. 9 Full local and non-local conductance matrix measurements.
The main text focuses on measurements of local conductances probed through each of the three normal contacts. For such measurements, the non-local responses are recorded in addition, not shown due to size constraints. Here two measurements are highlighted, for the charge configuration shown in Extended Data Fig. 4g. a. Local and non-local conductances when detuning VQDM, compared to b. numerical simulations of detuning μM. Strikingly, the ZBPs do not appear in the non-local measurements, as expected due to arising from MBSs localised on the outer QDs. Additionally, the same patterns of positive and negative non-local conductance in GML and GLM are observed, with the sign inverting at μ = 0. Unlike the simulations, signals appear in GRM, GLR, GRL and GRM that are not captured by the effective model. We note that a more complete model incorporating explicitly the hybrid regions such as in30 may be needed to fully describe all non-local effects. c. Local and non-local conductances when simultaneously detuning VQDL, VQDM and VQDR, compared to d. numerical simulations of detuning all μi.
Extended Data Fig. 10 Details of measurement procedure for Fig. 4.
In the main text, Fig. 4 highlights zero-bias conductance measurements at a three-site sweet spot, when simultaneously varying VQDL, VQDM and VQDR against simultaneously sweeping \({V}_{{\rm{ABS}}}^{{\rm{(1)}}}\) and \({V}_{{\rm{ABS}}}^{{\rm{(2)}}}\). Here, we detail how these measurements are performed. a. shows a repetition of the data as shown in Fig. 4e. First, the sweet spot values for \({V}_{{\rm{ABS}}}^{{\rm{(1)}}}\) and \({V}_{{\rm{ABS}}}^{{\rm{(2)}}}\) were determined from measuring CSDs, through the process shown in Fig. 1. We denote these values \(\delta {V}_{{\rm{ABS}}}^{(1)}=0\) and \(\delta {V}_{{\rm{ABS}}}^{(2)}=0\) respectively. Next, we apply 15 mV to each, with respect to these sweep spot voltages, in the direction that results in an avoided crossing signifying t > Δ. Due to cross-coupling, the resonance value for each QD needs to be re-determined. This is done by measuring the zero-bias Coulomb resonance for each QD, with the two other QDs set off resonance, and fitting a Lorentzian line-shape to determine the centre. b. and c. show CSDs measured at these VABS values for the left-middle and middle-right pairs respectively, taken for verification of the interdot coupling. Both sides show an antidiagonal avoided crossing signifying ti > Δi. The centers as obtained by the centering procedure are marked by the crosses. After centering, all three QDs are brought on resonance and swept simultaneously, accounting for differences in leverarms (see Extended Data Fig. 8). Here the orange line-trace in (a) is obtained, shown in d. The same procedure is repeated for every set-point, until reaching \({V}_{{\rm{ABS}}}^{{\rm{(1)}}}\), \({V}_{{\rm{ABS}}}^{{\rm{(2)}}}\) = + 15 mV. Now both CSDs show a clear diagonal avoided crossing, shown in e. and f. The new centers are marked, differing within a few mV from those in (b)/(c). The green dashed lines mark the paths taken by the simultaneous sweep for the green line in (a), plotted in g.
Extended Data Fig. 11 Reproduction of main results in a separate cooldown.
The measurements in Fig. 4 were repeated for validation during a separate cooldown of the same device. First, two-site sweet spots were obtained for both two-site pairs, as in Fig. 1. a. CSDs for resonances in the left and middle QD, varying \({V}_{{\rm{ABS}}}^{{\rm{1}}}\) in a range where the avoided crossing changes direction to determine the sweet spot (panel ii). Similarly, a sweet spot was obtained for the middle and right QD, upon varying \({V}_{{\rm{ABS}}}^{{\rm{2}}}\), shown in b. The magnetic field Bz corresponding to ϕΔ= 0 was determined from the spectroscopy measurements shown in Extended Data Fig. 5g. c. In this configuration, the measurement shown in Fig. 4 was repeated, using the same procedure as detailed in Extended Data Fig. 10. Additionally, we reproduce here the conductance spectra at the sweet spot as a function of d. detuning VQDR, e. detuning both VQDL and VQDR and f. detuning simultaneously all 3 QDs.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
ten Haaf, S.L.D., Zhang, Y., Wang, Q. et al. Observation of edge and bulk states in a three-site Kitaev chain. Nature 641, 890–895 (2025). https://doi.org/10.1038/s41586-025-08892-5
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-08892-5
This article is cited by
-
Unified model for non-Abelian braiding of Majorana and Dirac fermion zero modes
Science China Physics, Mechanics & Astronomy (2026)
-
Josephson diode effect in nanowire-based Andreev molecules
Communications Physics (2025)