Abstract
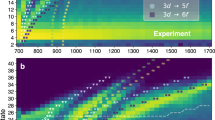
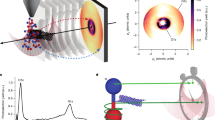
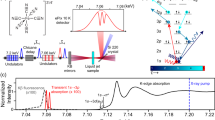
Coherent nonlinear light–matter interaction with X-rays gives access to a regime in ultrafast spectroscopy in which atomic resolution meets femtosecond and attosecond timescales1,2. Particularly, X-ray four-wave mixing, involving several resonant transitions in a single coherent nonlinear process, has the potential to provide information on the electronic states coupling, coherent electron motion, correlation and dynamics, with state and site selectivity3,4,5. Here we demonstrate coherent, background-free four-photon interactions with core-shell electrons using single broadband X-ray pulses from a free-electron laser. The all-X-ray four-wave mixing signals, measured in gaseous neon, arise from doubly resonant nonlinear processes involving Raman transitions6, including X-ray coherent anti-Stokes electronic Raman scattering. The 2D spectral maps (photon-in/photon-out) represent a step towards multidimensional correlation spectroscopy at the atomic scale. Using a multicolour time-delayed X-ray pulse scheme, we further demonstrate the feasibility of extending the proposed methodology to the ultrafast time domain. These results reveal potential for studying localized electron dynamics in multiple systems, from biomolecules to correlated quantum materials, with applications in areas such as energy conversion, biomedical imaging and quantum information technologies.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The raw data used in this study are available in a collaborative manner at the PSI Public Data Repository: https://doi.org/10.16907%2F7a7bd9c2-3258-454f-96cd-4c8f9d46464c.
Code availability
Data analysis codes are available on request. The codes for the model are available in a collaborative manner on request.
References
Mukamel, S., Healion, D., Zhang, Y. & Biggs, J. D. Multidimensional attosecond resonant X-ray spectroscopy of molecules: lessons from the optical regime. Annu. Rev. Phys. Chem. 64, 101–127 (2013).
Leone, S. R. & Neumark, D. M. Probing matter with nonlinear spectroscopy. Science 379, 536–537 (2023).
Tanaka, S. & Mukamel, S. Coherent X-ray Raman spectroscopy: a nonlinear local probe for electronic excitations. Phys. Rev. Lett. 89, 043001 (2002).
Kraus, P. M., Zürch, M., Cushing, S. K., Neumark, D. M. & Leone, S. R. The ultrafast X-ray spectroscopic revolution in chemical dynamics. Nat. Rev. Chem. 2, 82–94 (2018).
Chergui, M., Beye, M., Mukamel, S., Svetina, C. & Masciovecchio, C. Progress and prospects in nonlinear extreme-ultraviolet and X-ray optics and spectroscopy. Nat. Rev. Phys. 5, 578–596 (2023).
Weninger, C. et al. Stimulated electronic X-ray Raman scattering. Phys. Rev. Lett. 111, 233902 (2013).
Mukamel, S. Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations. Annu. Rev. Phys. Chem. 51, 691–729 (2000).
Jonas, D. M. Two-dimensional femtosecond spectroscopy. Annu. Rev. Phys. Chem. 54, 425–463 (2003).
Jonas, D. M. Optical analogs of 2D NMR. Science 300, 1515–1517 (2003).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786 (2007).
Stone, K. W. et al. Two-quantum 2D FT electronic spectroscopy of biexcitons in GaAs quantum wells. Science 324, 1169–1173 (2009).
Kolano, C., Helbing, J., Kozinski, M., Sander, W. & Hamm, P. Watching hydrogen-bond dynamics in a β-turn by transient two-dimensional infrared spectroscopy. Nature 444, 469–472 (2006).
Zumbusch, A., Holtom, G. R. & Xie, X. S. Three-dimensional vibrational imaging by coherent anti-Stokes Raman scattering. Phys. Rev. Lett. 82, 4142–4145 (1999).
Zhang, C., Zhang, D. & Cheng, J.-X. Coherent Raman scattering microscopy in biology and medicine. Annu. Rev. Biomed. Eng. 17, 415–445 (2015).
Marino, A. M., Pooser, R. C., Boyer, V. & Lett, P. D. Tunable delay of Einstein–Podolsky–Rosen entanglement. Nature 457, 859–862 (2009).
Camacho, R. M., Vudyasetu, P. K. & Howell, J. C. Four-wave-mixing stopped light in hot atomic rubidium vapour. Nat. Photonics 3, 103–106 (2009).
Dudovich, N., Oron, D. & Silberberg, Y. Single-pulse coherently controlled nonlinear Raman spectroscopy and microscopy. Nature 418, 512–514 (2002).
Ideguchi, T. et al. Coherent Raman spectro-imaging with laser frequency combs. Nature 502, 355–358 (2013).
Weber, T. et al. Complete photo-fragmentation of the deuterium molecule. Nature 431, 437–440 (2004).
Sansone, G., Pfeifer, T., Simeonidis, K. & Kuleff, A. I. Electron correlation in real time. ChemPhysChem 13, 661–680 (2011).
Bencivenga, F. et al. Nanoscale transient gratings excited and probed by extreme ultraviolet femtosecond pulses. Sci. Adv. 5, eaaw5805 (2019).
Harrington, P. M., Mueller, E. J. & Murch, K. W. Engineered dissipation for quantum information science. Nat. Rev. Phys. 4, 660–671 (2022).
Avisar, D. & Tannor, D. J. Complete reconstruction of the wave function of a reacting molecule by four-wave mixing spectroscopy. Phys. Rev. Lett. 106, 170405 (2011).
Schwickert, D. et al. Electronic quantum coherence in glycine molecules probed with ultrashort X-ray pulses in real time. Sci. Adv. 8, eabn6848 (2022).
Fulde, P. Electron Correlations in Molecules and Solids (Springer, 2012).
Ossiander, M. et al. Attosecond correlation dynamics. Nat. Phys. 13, 280–285 (2017).
Wang, Y., Wu, H., McCandless, G. T., Chan, J. Y. & Ali, M. N. Quantum states and intertwining phases in kagome materials. Nat. Rev. Phys. 5, 635–658 (2023).
Ernst, R. R., Bodenhausen, G. & Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions (Oxford Univ. Press, 1990).
Tanaka, S. & Mukamel, S. X-ray four-wave mixing in molecules. J. Chem. Phys. 116, 1877–1891 (2002).
Popmintchev, D. et al. Near- and extended-edge x-ray-absorption fine-structure spectroscopy using ultrafast coherent high-order harmonic supercontinua. Phys. Rev. Lett. 120, 093002 (2018).
Rouxel, J. R. et al. Hard X-ray transient grating spectroscopy on bismuth germanate. Nat. Photonics 15, 499–503 (2021).
Morillo-Candas, A. S. et al. Time resolved hard X-ray/optical transient grating spectroscopy on a liquid jet. In Proc. 2023 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC) (IEEE, 2023).
Ferrari, E. et al. All hard X-ray transient grating spectroscopy. Commun. Phys. 8, 257 (2025).
Cavaletto, S. M., Keefer, D. & Mukamel, S. High temporal and spectral resolution of stimulated X-ray Raman signals with stochastic free-electron-laser pulses. Phys. Rev. X 11, 011029 (2021).
Belabas, N. & Jonas, D. M. Three-dimensional view of signal propagation in femtosecond four-wave mixing with application to the boxcars geometry. J. Opt. Soc. Am. B 22, 655–674 (2005).
Müller, A. et al. Photoionization of Ne atoms and Ne+ ions near the K edge: precision spectroscopy and absolute cross-sections. Astrophys. J. 836, 166 (2017).
Williams, S., Rohlfing, E. A., Rahn, L. A. & Zare, R. N. Two-color resonant four-wave mixing: analytical expressions for signal intensity. J. Chem. Phys. 106, 3090–3102 (1997).
Gel’mukhanov, F., Sałek, P., Privalov, T. & Ågren, H. Duration of x-ray Raman scattering. Phys. Rev. A 59, 380–389 (1999).
Rohringer, N. et al. Atomic inner-shell X-ray laser at 1.46 nanometres pumped by an X-ray free-electron laser. Nature 481, 488–491 (2012).
Li, K., Labeye, M., Ho, P. J., Gaarde, M. B. & Young, L. Resonant propagation of x rays from the linear to the nonlinear regime. Phys. Rev. A 102, 053113 (2020).
Frasinski, L. et al. Dynamics of hollow atom formation in intense X-ray pulses probed by partial covariance mapping. Phys. Rev. Lett. 111, 073002 (2013).
Hennies, F. et al. Resonant inelastic scattering spectra of free molecules with vibrational resolution. Phys. Rev. Lett. 104, 193002 (2010).
Lundberg, M. & Wernet, P. Resonant Inelastic X-ray Scattering (RIXS) Studies in Chemistry: Present and Future, 1–52 (Springer, 2019).
Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).
de Groot, F. M. et al. Resonant inelastic X-ray scattering. Nat. Rev. Methods Primers 4, 45 (2024).
Guo, Z. et al. Experimental demonstration of attosecond pump–probe spectroscopy with an X-ray free-electron laser. Nat. Photonics 18, 691–697 (2024).
Li, S. et al. Attosecond-pump attosecond-probe x-ray spectroscopy of liquid water. Science 383, 1118–1122 (2024).
Meier, T., Schulze, A., Thomas, P., Vaupel, H. & Maschke, K. Signatures of Fano resonances in four-wave-mixing experiments. Phys. Rev. B 51, 13977–13986 (1995).
Ott, C. et al. Lorentz meets Fano in spectral line shapes: a universal phase and its laser control. Science 340, 716–720 (2013).
Li, K. et al. Super-resolution stimulated X-ray Raman spectroscopy. Nature 643, 662–668 (2025).
Eckbreth, A. C. BOXCARS: crossed-beam phase-matched cars generation in gases. Appl. Phys. Lett. 32, 421–423 (1978).
Prior, Y. Three-dimensional phase matching in four-wave mixing. Appl. Opt. 19, 1741–1743 (1980).
Vdovin, G. & van Goor, F. LightPipes for Python. Github https://opticspy.github.io/lightpipes/ (2023).
Prat, E. et al. An X-ray free-electron laser with a highly configurable undulator and integrated chicanes for tailored pulse properties. Nat. Commun. 14, 5069 (2023).
Pradervand, C. et al. A compact gas attenuator for the SwissFEL ATHOS beamline realized using additive manufacturing. J. Synchrotron Radiat. 30, 717–722 (2023).
Al Haddad, A. et al. High magnification optical imaging systems for the characterization of soft X-ray focii. J. Synchrotron Radiat. 32, 1479–1490 (2025).
Boyd, R. W., Gaeta, A. L. & Giese, E. in Springer Handbook of Atomic, Molecular, and Optical Physics, 1097–1110 (Springer, 2023).
Lutman, A. et al. Fresh-slice multicolour X-ray free-electron lasers. Nat. Photonics 10, 745–750 (2016).
Reiche, S. & Prat, E. Two-color operation of a free-electron laser with a tilted beam. J. Synchrotron Radiat. 23, 869–873 (2016).
Prat, E. et al. Widely tunable two-color X-ray free-electron laser pulses. Phys. Rev. Res. 4, L022025 (2022).
Wang, G., Dijkstal, P., Reiche, S., Schnorr, K. & Prat, E. Millijoule femtosecond X-ray pulses from an efficient fresh-slice multistage free-electron laser. Phys. Rev. Lett. 132, 035002 (2024).
Prior, Y. & Ben-Reuven, A. Nonimpact theory of four-wave mixing and intracollisional dynamics. Phys. Rev. A 33, 2362–2377 (1986).
Rohringer, N. & London, R. Atomic inner-shell X-ray laser pumped by an X-ray free-electron laser. Phys. Rev. A 80, 013809 (2009).
Pfeifer, T., Jiang, Y., Düsterer, S., Moshammer, R. & Ullrich, J. Partial-coherence method to model experimental free-electron laser pulse statistics. Opt. Lett. 35, 3441–3443 (2010).
Frasinski, L. J., Codling, K. & Hatherly, P. A. Covariance mapping: a correlation method applied to multiphoton multiple ionization. Science 246, 1029–1031 (1989).
Acknowledgements
We acknowledge the technical support of S. Tiefenbacher and all of the groups involved in the operation of SwissFEL. The research leading to these results has received support from the Swiss National Science Foundation under grant agreement no. 200021-165550/1. The Maloja instrument received support from the Swiss National Science Foundation through R’Equip grant no. 206021-182988. The work of A.S.M.-C. was financed by the European Union’s Horizon 2020 programme under the Marie Skłodowska-Curie grant agreement 884104 (PSI-FELLOW-III-3i).
Author information
Authors and Affiliations
Contributions
G.K. initiated and led the project. G.K. and A.S.M.-C. coordinated the project. G.K. and C.B. supervised the project and managed the funding acquisition. G.K. and T.P. developed the experimental concept and T.F. and A.C. provided advice on the experimental plan. K.S., A.A.-H., A.S., Z.S., N.Y., A.S.M.-C. and G.K. prepared the experimental beamline. E.P. prepared the X-ray pulses, in particular the set-up of the two-colour mode. All authors participated in the collection and interpretation of the experimental data. A.S.M.-C. led the data analysis, with support from S.A., J.K. and S.Z. A.S.M.-C., S.A. and G.K. developed the model and set up the required computational resources for the simulations. A.S.M.-C. and G.K. prepared the initial version of the manuscript. T.P., C.O., T.F., K.S. and A.A.-H. provided feedback on the initial draft. T.P., C.O. and T.F. provided feedback to the corresponding authors, A.S.M.-C. and G.K., in preparing the submitted manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Laura Foglia and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Beam propagation in the sample.
a, Calculation of the beam distribution at two positions before entering the gas cell. b,c, Propagation around the focus. c, Intensity distribution at the focus.
Extended Data Fig. 2 BoxCARS geometry.
a, Coordinate system and arrangement of beams on the mask used for the phase-matching calculation. The holes of the spatial mask have diameters of 1 mm and therefore cover a range of angles on the order 2Θmax − 2Θmin ≈ 0.04°. b, Phase-matching efficiency (sinc2 function in equation (4)) calculated for the case of ω1 = ω2 = 867 eV, a fixed θ = θ3 = θS, as a function of a varying ω3. The refractive index value is approximated to 1 and the propagation length is set as large as the gas cell, 8 mm, thus showing an unrealistic ‘worst-case scenario’ for phase mismatch. A shorter length value would increase the phase-matching energy/angle tolerance.
Extended Data Fig. 3 Spatial characterization of the XFWM signal.
To compare the signal beam with the incoming beams, we compare the images taken with a Ce-YAG screen located after the sample with and without the incoming beam open (that is, four holes or three holes opened in the spatial mask). a, Incoming beam opened in the signal direction (four holes opened in the mask). The photon energy was set at 876 eV. b, Same image as in panel a but scaled similarly as for the signal beam (see panel c) for comparison. c, XFWM signal detected with three holes opened in the spatial mask at the same photon energy, 876 eV. The signal beam profile is similar to the open incoming beam case. d, The XFWM signal vanishes when only two holes in the mask are opened, as expected from a FWM signal. The measurement in panel d was taken at 866.8 eV, around the maximum signal strength (see Fig. 1f). All measurements were done with the same gas pressure of 800 mbar. Each image is the average of 2,000 FEL shots.
Extended Data Fig. 4 Verification of the XFWM signal at 800 mbar.
Spectral maps recorded in the same experimental conditions but with different number and position of holes opened in the spatial mask. a, Standard measurement configuration, that is, three holes of the spatial mask open, only one incoming beam closed. b,c, Photon energy maps measured closing two of the incoming beams (two beams only reaching the sample). An indicative scheme of each mask and beam block configuration is shown as inset in the three 2D spectral maps. All measurements were done with the same gas pressure of 800 mbar and 25 fs r.m.s. pulse duration.
Extended Data Fig. 5 Verification of the XFWM signal at 200 mbar.
Spectral maps recorded in the same experimental conditions but with different number and position of holes opened in the spatial mask. a, Standard measurement configuration, that is, three holes of the spatial mask open, only one incoming beam closed. b,c, Photon energy maps measured closing two of the incoming beams. An indicative scheme of each mask and beam block configuration is shown as inset in the three 2D spectral maps. All measurements were done with the same gas pressure of 200 mbar and 25 fs r.m.s. pulse duration.
Extended Data Fig. 6 Pressure dependency of the XFWM spectra.
Photon energy scans for: 800 mbar (a), 400 mbar (b) and 200 mbar (c) measured with a pulse duration of 25 fs r.m.s. and plotted as spectral maps as a function of the incoming and detected photon energies.
Extended Data Fig. 7 Reference measurement, with no sample.
Photon energy map measured with three incoming beams and a gas pressure of 0.1 mbar.
Extended Data Fig. 8 Schematic energy diagrams for the XFWM processes considered in the model.
a, Two-colour XFWM (also valid for XSRS). b, Degenerate (for |f⟩ = |e⟩) or quasi-degenerate processes. c, XTG process.
Extended Data Fig. 9 Intensity scans.
a, Average spectra measured for different FEL transmissions at 800 mbar, 876.6 eV FEL photon energy and 25 fs r.m.s. pulse duration. The black lines show the region of interest taken for the fit. b, Integrated signal within the range indicated by the vertical lines in panel a, plotted as a function of intensity (FEL transmission), together with the corresponding fit and a power-three law simulation. c, Spectra measured for different FEL transmissions at 800 mbar, 866.4 eV FEL photon energy and 25 fs r.m.s. pulse duration. The black lines show the region of interest taken for the fit shown in panel d. d, Integrated signal within the range indicated by the vertical lines in panel c, plotted as a function of intensity (FEL transmission), together with the corresponding fit and a power-three law simulation. e, Spectra measured for different FEL transmissions at 200 mbar, 866.8 eV FEL photon energy and 25 fs r.m.s. pulse duration. f, Integrated signal within the range indicated by the vertical lines in panel e, plotted as a function of intensity (FEL transmission), together with the corresponding fit and a power-three law simulation. The error is calculated as the standard deviation within all shots.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Morillo-Candas, A.S., Augustin, S., Prat, E. et al. Coherent nonlinear X-ray four-photon interaction with core-shell electrons. Nature 649, 590–596 (2026). https://doi.org/10.1038/s41586-025-09911-1
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-09911-1