A comparison of methods to assess cell mechanical properties

Abstract

The mechanical properties of cells influence their cellular and subcellular functions, including cell adhesion, migration, polarization, and differentiation, as well as organelle organization and trafficking inside the cytoplasm. Yet reported values of cell stiffness and viscosity vary substantially, which suggests differences in how the results of different methods are obtained or analyzed by different groups. To address this issue and illustrate the complementarity of certain approaches, here we present, analyze, and critically compare measurements obtained by means of some of the most widely used methods for cell mechanics: atomic force microscopy, magnetic twisting cytometry, particle-tracking microrheology, parallel-plate rheometry, cell monolayer rheology, and optical stretching. These measurements highlight how elastic and viscous moduli of MCF-7 breast cancer cells can vary 1,000-fold and 100-fold, respectively. We discuss the sources of these variations, including the level of applied mechanical stress, the rate of deformation, the geometry of the probe, the location probed in the cell, and the extracellular microenvironment.

Main

Cells in vivo are continuously subjected to mechanical forces, including shear, compressive, and extensional forces (Fig. 1; definitions of important terms in biomechanics are provided in Supplementary Note 1). The ability of cells to deform and actively respond to mechanical forces is critical for embryonic development and for homeostasis in adult tissues and organs. Cell mechanics is the factor that defines the cellular response to the mechanical forces exerted by the cell’s microenvironment, including neighboring cells and the extracellular matrix¹. This cellular response can be viscous, elastic, or viscoelastic, as well as passive or active. The recent development of tools for measuring cell mechanics has revealed that changes in cell and nuclear mechanics are hallmarks of many human diseases, particularly metastatic cancer, cardiovascular disease, inflammation, laminopathies, host–microbe interactions in infectious diseases, and frailty in aging^2,3,4,5,6. Values of cell elasticity (the stretchiness of cells) and viscosity (a measure of viscous dissipation) reported in the literature vary considerably even among groups that used the same instruments. One contributor to these variations is often assumed to be differences in cell-culture conditions (subtle differences in temperature, pH, cell passage number, etc.), which prevent direct comparisons among datasets and may have slowed down the translation of cell mechanics instruments for clinical applications.

Fig. 1: Description of rheological tests.

a, Different geometries of deformation. To test the mechanical properties of a material, one can stretch or compress it (left) or apply a mechanical shear stress (right). During stretching, the deformation of the material results from a pulling force F perpendicular to the surface of the sample. Similarly, compression corresponds to deformation (shortening) that results from a pushing force perpendicular to the surface area. In contrast, a shear test involves deformations that occur when the force is applied parallel (tangential) to the surface of the sample. b, Constant or oscillating applied stress. A creep test consists in the application of a constant stress (σ = F₀/A) over time and recording of the resulting deformation ε(t) of the sample (left). For a dynamic test, the applied force oscillates, thereby resulting in an oscillatory deformation of the sample (right). c, Examples of material responses for a creep test and a dynamic test for a purely elastic material, a purely viscous fluid, and a viscoelastic material. T is the period of oscillation.

In this work, we measured and compared the mechanical properties of the commonly used MCF-7 human breast cancer cells, cultured in the same environmental conditions in vitro, by applying seven different technologies, including atomic force microscopy (AFM), magnetic twisting cytometry (MTC), particle-tracking microrheology (PTM), parallel-plate rheometry, cell monolayer rheology (CMR), and optical stretching (OS). Overall, although the underlying mechanical principles remain the same, our measurements highlight how cell mechanics depends on the level of mechanical stress and rate of deformation to which the cell is subjected, the geometry of the mechanical probe used in the experiments, the probe–cell contact area, the probed location in the cell (e.g., cell cortex, nucleus, lamella, or cytoplasm), and the extracellular context (monolayer of cells versus single cells, adherent versus free-floating cells, etc.). Our results also highlight how mechanical properties of cells can vary by orders of magnitude, depending on the length scale at which cell viscoelasticity is probed, from tens of nanometers (e.g., the diameter of an actin fiber) to several micrometers (the size of a whole cell).

Results

To ensure consistency, we obtained the measurements presented below in a total of eight different laboratories using MCF-7 cells from the same lot, cultured in medium from the same lot, all directly provided by ATCC. We measured the mechanical properties of these cells by AFM, MTC, PTM, parallel-plate rheometry, CMR, and OS. Details of the techniques used by the participating laboratories are presented in Supplementary Table 1. Different moduli were measured by different methods; a detailed description of moduli and their inter-relationships can be found in Supplementary Note 2. Among the methods tested in this study, AFM, parallel-plate rheometry, and OS all provide measurements of Young’s modulus (E), whereas MTC, CMR, and PTM all provide measurements of the shear modulus (G).

Atomic force microscopy

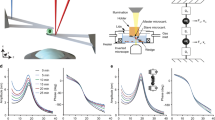
AFM-based indentation is commonly used to quantify the mechanical properties of adherent cells at subcellular resolution (Fig. 2a,b). An atomic force microscope consists of a cantilever of calibrated stiffness that applies a preset force or deformation at a defined speed onto an adherent cell or tissue and, through laser deflection and detection by a photodetector (Fig. 2a), measures the corresponding resisting force from the deformation of the cell (Fig. 2b). A 3D piezo scanner allows one to measure x, y, and z displacements of the cantilever relative to the underlying cell (Fig. 2a). Here we indented MCF-7 cells with nanoscale pyramidal probes (radius of the probe apex: ~10 nm), mesoscale spheroconical probes (radius: ~750 nm), and microscale spherical probes (radius: ~5 μm) (Fig. 2c).

Fig. 2: AFM measurements.

For these measurements we used sharp conical AFM probes, conospherical probes of radius 750 nm, and spherical probes of radius 2,500 nm. a, Schematic of the measurement of cell mechanics. An AFM probe with well-defined geometry is used to indent a cell along the vertical z-axis. b, Force curves from AFM showing the force F versus the vertical position z of the cell. Typical force curves for mechanically soft and hard samples are shown. c, Average elastic moduli obtained with various AFM probes under different conditions (vertical indenting speed v and surrounding temperature T). Error bars indicate s.d. d,f,h, Raw AFM force data (F versus z) obtained with sharp conical probes (d), the dull conospherical probe (semi-vertical angle, ~22.5°) (f), and the spherical probes (h). e,g,i, Histograms and cumulative probabilities of the elastic modulus obtained for indentation depths of 0–300 nm, corresponding to d,f,h, respectively. The appropriate model was used for each type of AFM probe: the Sneddon model for the sharp conical probes (e), and the Hertz model for the dull conospherical probe (g) and spherical probes (i). Sample temperatures and indenting speeds are shown in the histograms. For the conical probe, 20 and 60 cells were measured at 25 °C at an indenting speed of 6 μm s^–1 and at 37 °C at an indenting speed of 2 μm s^–1, respectively. For the spherical probes, 30, 10, and 20 cells were measured at 37 °C and 2 μm s^–1 with the 750-nm-radius probe, at 25 °C and 6 μm s^–1 with the 2,500-nm-radius probe, and at 37 °C and 10 μm s^–1 with the 2,500-nm-radius probe, respectively.

We measured the elastic (effective Young’s) modulus of the cells by fitting the curves of the measured force as a function of the vertical position of the cantilever using so-called elastic contact models that account for the geometry of the indentation (Methods). Our measurement with a nanoscale AFM probe showed that the mechanical properties of cells are heterogeneous and vary considerably from cell to cell (Fig. 2d,e). For ~1-µm indentations produced at a speed of 2 µm s^–1 with a sharp tip—both of which are typical values for this method—the average static effective Young’s elastic modulus of MCF-7 cells was 5.5 ± 0.8 kPa (mean ± s.d.; n = 60) over the central nuclear region and 3.8 ± 0.5 kPa over flat regions of the cell body, between the nucleus and the cell edge. Higher indentation speeds resulted in higher elastic moduli of 10.5 ± 0.5 kPa (Fig. 2c–e).

When cells are indented with a larger probe (Fig. 2f,g), AFM measurements are less sensitive to local cell heterogeneity, and the elastic modulus is substantially lower. Indentation of the nuclear region by probes with an intermediate apex radius (~0.75 μm) at a speed of 2 μm s^–1 yielded an elastic modulus of 0.58 ± 0.23 kPa, computed via the ‘blunted indenter’ contact model^7,8. With the Hertz model of indentation⁹, 5-μm-diameter glass beads attached to tipless cantilevers (Fig. 2h,i) and an indentation depth of ~300 nm yielded elastic moduli of 0.53 ± 0.52 kPa for an indentation speed of 10 µm s^–1 at 37 °C, and 0.81 ± 0.06 kPa for 6 µm s^–1 at room temperature. Together, these results show that the mechanical properties of cells measured by AFM can differ more than tenfold, depending on the measurement parameters and the probed regions of the cells.

Whole-cell deformation measurements

Once MCF-7 cells are detached from their underlying substrates, they round up (similarly to cancer cells in blood vessels after intravasation) and can be kept alive in suspension for a few hours. To measure the viscoelastic properties of cells in suspension, one must use methods that preserve this suspended state, such as parallel-plate rheometry and OS.

Parallel-plate rheometry

The parallel-plate rheometer extracts the Young’s (extensional) modulus and deformability (i.e., compliance) at the global cellular scale¹⁰. A single cell is placed between a rigid plate and a flexible plate of calibrated stiffness k that is used as a force probe, and the cell is stretched through constant or oscillatory displacements (Fig. 3a). For oscillatory displacements of plates with frequency ω (Fig. 1), the elastic (storage) and viscous (loss) moduli, E′(ω) and Eʺ(ω), respectively, are weak power laws of the frequency: E′(ω) ~ Eʺ(ω) ~ ω^α, with α << 1 (Fig. 3b). The exponent α of this power law estimates the balance between dissipative and elastic behaviors: a higher exponent signifies higher viscous dissipation; in particular, α = 0 for a purely elastic solid (e.g., rubber), whereas α = 1 for a viscous liquid (e.g., water). For MCF-7 cells at a frequency of 1 Hz, the viscous modulus E₀ʺ was 340 ± 40 Pa, the elastic modulus E₀′ was 950 ± 150 Pa (Fig. 3c,d), and α was 0.18 ± 0.01, indicating a predominantly elastic response.

Fig. 3: Whole-cell deformation measurements.

a–d, Cells between surfaces. a, Schematic of the parallel-plate rheometer. An oscillating displacement D(ω) is applied at the base of the flexible microplate, and the resulting displacement d(ω) at the tip of the microplate is recorded. The force applied to the cell is proportional to the flexible plate deflection δ: F = kδ. The picture in the lower left represents a side view of an MCF-7 cell between the microplates. Scale bar, 10 µm. b, Elastic (E′; blue squares) and viscous (Eʺ; red circles) extensional moduli as a function of frequency for a single MCF-7 cell in a log–log graph, showing weak power-law behavior. c,d, Distributions of viscous (c) and elastic (d) moduli (n = 18 cells). The viscous and elastic moduli were 340 ± 50 Pa and 950 ± 140 Pa (mean ± s.d.), respectively. e, Schematic of OS: two diverging, counter-propagating laser beams emanating from single-mode optical fibers trap cells at low power as they are being flowed into the trapping region via a microfluidic channel (left) and then stretch them at higher powers (right). f, Strain and compliance profiles for each cell measured by OS. Cells (n = 514 cells) were trapped for 2 s at 0.2 W per fiber and stretched for 8 s (red portion of graph) at 0.75 W per fiber. The black curve shows the average strain and compliance for the entire population. The average peak strain (at t = 8 s) was 5.16% ± 0.11%; the average peak compliance was 0.053 ± 0.001 Pa⁻¹. The white triangle indicates a linear increase in strain, suggesting a dominant viscous behavior. Dark gray curves represent the average profiles of the lighter gray curves. The pink shading at the edges of the graph indicate the time windows of pre- and post-stretching. g, Distribution of steady-state viscosity obtained by fitting the compliance results for each cell to the so-called standard linear liquid model. The steady-state viscosity was 158 ± 84 Pa s^–1 (mean ± s.d.). h, Distribution of elastic moduli obtained from the standard linear liquid model fitting, where the elastic modulus obtained was 18 ± 24 Pa (mean ± s.d.). Dashed lines represent cumulative distributions in c,d,g,h.

The parallel-plate rheometer also measures the relaxation and creep functions of individual cells, that is, the evolution of stress under constant strain and the deformation under constant stress, respectively. MCF-7 cells showed a weak power-law behavior with an extensional modulus ${E}_{0}=\sqrt{{E}_{0}^{^{\prime} 2}+{E}_{0}^{^{\prime\prime} 2}}$ = 1,020 ± 150 Pa at 1 Hz (Supplementary Fig. 1). Moreover, when we applied static cell elongation and measured the corresponding lateral cell deformation, we found a Poisson’s ratio ν of 0.33. We estimated the shear modulus G₀ as E₀/2(1 + ν) = 380 Pa at 1 Hz.

Optical stretching

The optical stretcher allows one to measure the creep compliance and modulus of single cells through the use of a dual-beam optical trap to induce well-defined mechanical stresses on whole cells in suspension^2,11,12. The forces that trap and deform the cell surface (Fig. 3e) through the transfer of momentum from the light to the cell are due to the change in the refractive index (RI) at the cell–medium interface¹². We measured the RI of MCF-7 cells by digital holographic microscopy and found an average RI of 1.374 ± 0.002 (mean ± s.e.m.; n = 89)¹³ (Supplementary Fig. 2). We computed the stress on the cells by using an electromagnetic wave model¹⁴. For convenient delivery of the cells into the trapping region, the optical stretcher is integrated into a microfluidic system (Fig. 3e), which enables measurement rates of >100 cells per hour.

In this study, we analyzed MCF-7 cells after each cell had been trapped for 2 s at a power of 0.2 W per fiber and stretched for 8 s at 0.75 W per fiber. We obtained an average peak strain (at t = 8 s after onset of stretching) of 5.16% ± 0.11% (Fig. 3f), with average peak compliance (i.e., deformability) of 0.053 ± 0.001 Pa⁻¹ (Fig. 3f). The creep compliance profile of cells reveals their composite viscous and elastic properties. The white triangle in Fig. 3f indicates a clear linear increase in strain (i.e., deformation) with time, demonstrating a dominant viscous behavior when the cells were in suspension. The inverse of the slope provides a first estimation of steady-state viscosity, which we found to be about 180 Pa s^–1. Fitting with finer models² yielded a viscosity of 158 ± 84 Pa s^–1 (Fig. 3g). We note here that this overwhelming dominance of viscosity over elasticity is not a feature of all cell types as measured by OS¹⁵. Elastic moduli obtained via standard linear liquid model fitting were 18 ± 24 Pa (Fig. 3h). Even with MCF-7 cells, stretching at higher laser powers produced creep curves with more pronounced elastic components (Supplementary Fig. 2d). Overall, whole-cell measurements of the elasticity of MCF-7 cells by parallel-plate rheometry and OS showed ~50-fold differences, with parallel plates leading to higher values. Notably, the measurements of elasticity obtained with parallel plates were in the same range as those obtained by AFM.

Multicellular measurements

CMR probes cells placed between two plates of a commercial rotational rheometer with a glass sensor and plate–ring geometry, which provides more accurate measurements in the regime of large shear deformations than the conventional plate–plate geometry¹⁶ (Fig. 4a). Fibronectin coating (2 µg cm^–2) of the plates enhances cell adhesion; cells form a sparse monolayer that can be observed through a microscope during measurements (Fig. 4a). The ring rotates around its symmetry axis, which leads to simultaneous shear deformation of the cells. At an oscillation frequency of 0.5 Hz, MCF-7 cells exhibit a decrease in shear modulus with increasing amplitude of the imposed shear deformation. The cell shear modulus G at a relative deformation of 0.1 is 4.6 ± 2.2 kPa. The cell elastic (stretching) modulus E was 12 ± 5.7 kPa, assuming a Poisson ratio of 0.3. We extracted elastic and viscous contributions to the cell shear modulus from the phase shift between excitation and cell response, G′ = 4.5 ± 2.2 kPa and Gʺ= 1.1 ± 0.5 kPa, corresponding to elastic and viscous stretching moduli Y′ = 12 ± 5.7 kPa and Yʺ = 3.9 ± 2.9 kPa, respectively (Fig. 4). At a constant relative deformation of 0.02, the cell shear modulus increased with increasing oscillation frequency to fit a power law with an exponent β = 0.065. Under constant load, single-cell creep compliances followed a power law in time with an exponent that decreased with increasing stress from approximately 0.1 to 0.01 (Methods). Overall, the elasticity of cells obtained by CMR was close to the elasticity measured by AFM with a conical probe.

Fig. 4: Cell monolayer rheology.

a, Schematic of the experimental setup; the image in the upper right is a differential interference contrast image of the cells. b, Deformation-controlled amplitude sweep: the Young’s modulus exhibits a decrease in cell stiffness with increasing oscillation amplitude at a constant frequency of 0.5 Hz. c, Frequency sweep: the cell shear modulus increases with increasing frequency at a constant shear deformation of 0.02 as a power law with an exponent β of 0.065 (n = 8). Error bars in b,c indicate s.d. d, Results of creep experiments at different applied stresses. The creep compliances follow power laws. e, Deformation–stress curves obtained from cyclic stress ramp experiments. We applied different rates of increasing stress, as shown in the key. For low rates, the deformation–stress curves exhibit nonlinear hysteresis (left x-axis, upper curve), which vanishes at high rates (right x-axis, lower curve).

Bead-based measurements

The magnetic twisting cytometer

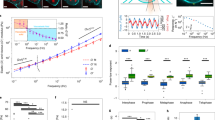
MTC uses an Arg-Gly-Asp-coated ferromagnetic bead bound to the apical surface of the MCF-7 cell^12,13 (Fig. 5a). We applied a controlled homogeneous magnetic field to the cell via magnetic coils, which caused the bead to translocate and rotate. We measured the stiffness of MCF-7 cells on the basis of the magnitude of the bead–cell area of contact (Fig. 5b), the magnetic field applied (Fig. 5c), and the displacement of the magnetic bead^14,15 (Fig. 5c). The shear modulus of MCF-7 cells G₀, calculated as $\sqrt{{G}_{0}^{^{\prime} 2}+{G}_{0}^{^{\prime\prime} 2}}$, was 0.69 ± 0.05 kPa; the elastic modulus G′ was 0.62 ± 0.04 kPa; and the viscous modulus Gʺwas 0.25 ± 0.02 kPa. Assuming a Poisson’s ratio of 0.3, Young’s modulus E₀ of MCF-7 cells was 1.78 ± 0.12 kPa, the elastic modulus E′ was 1.62 ± 0.11 kPa, and the viscous modulus Eʺ was 0.66 ± 0.06 kPa (Fig. 5d).

Fig. 5: Bead-based measurements.

a–d, Magnetic twisting cytometry. a, Schematic of the MTC process. The dashed circle denotes the position of the bead before twisting, the dashed arrow indicates the magnetic twist force, the white arrow indicates the direction of the bead magnetic moment, and the dashed vertical lines indicate the displacement of the bead. RGD, Arg-Gly-Asp. b, Quantification of magnetic beads bound to or embedded in MCF-7 cells. We estimated bead embedment (~30%) by measuring the actin ring diameter from the fluorescent image (dashed white circle) and comparing it to the bead diameter from the brightfield image (white arrows). Scale bars, 10 μm. c, Application of a continuous magnetic field of 50 G with stress modulation (17.5-Pa peak stress) and displacement of the magnetic beads as a function of cyclic force (0.3 Hz). For visual clarity, data from only 10 representative beads out of a total of 193 beads are shown. d, The elasticity of MCF-7 cells as measured by MTC (n = 193 beads). e–l, Particle-tracking microrheology. e, Representative phase contrast image of an MCF-7 cell with fluorescent beads (red circles) after recovery. Scale bar, 15 μm. f, Zoomed-in image of a fluorescent bead (diameter, 100 nm; outlined by a black box in e) inside a cell. Scale bar, 10 μm. g, Trajectory corresponding to the bead shown in f. Scale bar, 200 nm. h, PTM measurements of 20 cells (>100 beads) from three separate preparations. Ensemble-averaged MSDs from three different cell-culture plates were identical (bottom right plot). i, The elastic modulus at 30 Hz as measured by PTM of cells from three different plates (n > 100 beads in each plate, with a total of 512 beads). One-way ANOVA showed that there was no significant difference between plates (NS; P = 0.30). j, The distribution of elastic and viscous moduli of MCF-7 cells from the plates. k, Creep compliance of MCF-7 cells calculated from the bead MSDs. l, Distribution of creep compliance (bars) and its cumulative distribution (dotted curve). In box-and-whisker plots (d,i,j), center lines indicate medians, edges of boxes define the 25th and 75th percentiles, whiskers extend to the 5th and 95th percentiles, and dots represent data points below or above the 5th or 95th percentile values.

Particle-tracking microrheology

For PTM, we ballistically injected submicrometer fluorescent beads into the cytoplasm or nucleus of cells, and then allowed the cells to recover in fresh medium overnight¹⁷. We measured spontaneous movements of the beads inside the cells with ~5-nm spatial resolution at a video rate of 30 frames per second for 20 s^17,18,19. We computed the mean square displacements (MSDs) of beads from the bead trajectories (Fig. 5e–g). The ensemble-averaged MSDs from three different cell-culture plates were identical (Fig. 5h). One-way analysis of variance (ANOVA) showed that there was no significant difference (P = 0.3) in the elastic modulus from three different plates measured at 30 Hz, thus suggesting consistent and reproducible results (Fig. 5i). At 1 Hz, the elastic modulus G′ was 4.5 ± 0.4 Pa, and the viscous modulus Gʺ was 10.1 ± 0.9 Pa (Fig. 5j). We were also able to calculate the creep compliance of the cytoplasm of MCF-7 cells from the MSDs of the beads (Fig. 5k). The peak incidence of creep compliance from beads was ~7 × 10⁻³ (1/Pa) (Fig. 5i). Together, these results demonstrate that the elasticity of cells measured by MTC is >100-fold higher than that measured by PTM, and that MTC measurements of cell elasticity are in the same range as AFM measurements.

Discussion

Mechanical forces play a major role in the regulation of the function and organization of cells, tissues, and organs. The modulus of a cell—a measure of its viscoelastic properties—is a key factor in how cells sense these forces and interact with other cells and the extracellular matrix. In this study, we measured the mechanical properties of cells by different methods, including AFM, PTM, OS, CMR, MTC, and parallel-plate rheometry. In principle, different types of rheological measurements should be related to each other if certain assumptions about the materials being measured are valid, yet the average values of moduli vary by at least two orders of magnitude (Table 1). In general, the results presented in Table 1 can be divided into three categories on the basis of the values of the obtained moduli: small (OS and PTM), intermediate (AFM with dull probes, parallel-plate rheometry, and MTC), and high (AFM with a sharp probe and CMR). The widely distributed mechanical measurements obtained in our study indicate that the mechanical response of cells to forces is highly dependent on the force profile. These methods differ widely in how the measurements are collected and what area of the cell is probed (Supplementary Table 1), which explains the differences in part. These results also highlight the importance of selecting an adequate technique for the biological question being addressed (Supplementary Table 1). Below we briefly discuss the main reasons for similarities and variations among different measurements; a more thorough discussion can be found in Supplementary Note 3.

Table 1 Overview of measurements

The methods that produce intermediate modulus values (AFM with a dull probe, MTC, and parallel-plate rheometry) share physical similarities in terms of how measurements are collected²⁰. Among the AFM measurements, measurements giving rise to smaller elastic moduli can be explained by the difference in the physics of the probe–cell contacts in these methods. Moduli derived from MTC data are about 60% higher than those derived by parallel-plate rheometry. The difference could be explained by the additional contact between the beads and microscopic roughness of the pericellular membrane (microvilli and microridges) in the MTC approach. Whereas forces are applied to the cell directly as a result of physical contact in AFM, parallel plates apply forces through molecular links developed between the plates and the cell body. In CMR, the measured elastic modulus is about an order of magnitude higher than the ones obtained via other probe-based methods, and this can presumably be explained by the increased level of tensile pre-stress²¹. Cells in CMR can undergo high tensile forces between plates because of the fibronectin coating^10,22,23. The positive association between pre-stress level and measured elastic modulus is also consistent with the observations of substantially higher moduli in AFM experiments with the sharp conical AFM probe compared with those obtained by different methods. Such a probe produces much higher stresses compared with those observed with dull probes. As a result, the cell presumably becomes overstretched and stiff, similar to what is observed with other soft materials and viscoelastic polymer solutions²⁴. In this study, MTC and CMR involved an ‘active’ mechanical measurement in which specific ligands were used. Mechanical measurements can propagate deeply into a cell through pre-stress and stiff actin bundles that guide the propagation of forces over long distances²⁵. This active mechanical measurement can be achieved with AFM and the parallel-plate method^10,22,23.

The elasticity of MCF-7 cells measured by OS was more than two orders of magnitude smaller than the elasticity measured by AFM or MTC. This difference is probably attributable to the fact that OS measures free-floating cells, whereas the other methods measure cells adhered to a rigid glass substrate. Given that it was shown that the modulus of weakly adherent MCF-7 cells does not change substantially²⁶, complete detachment of cells from the surface may be required to mechanically ‘relax’ cells. The location of probes relative to cells can also affect mechanical measurements, and it has been shown that cell nuclei are typically harder than the cell periphery^{8,26,27,28,29,30}. PTM yielded the lowest elastic moduli out of all the techniques tested in this study. It is likely that this is due to the low pre-stress in PTM measurements; also, this method can probe mechanical properties of the cytosol³¹.

For further comparison of the various measurement methods, analytical models based on the physics principles of each method are used, and with these certain assumptions are introduced, such as linear elasticity for AFM or viscoelastic behavior for the other methods. The second assumption underlying most mechanical measurements of cells is that the Poisson’s ratio is close to 0.5, or at least is a constant. However, recent work indicates that the cytoplasm of living cells can behave as a poroelastic material. Thus the common assumption that the Poisson’s ratio is a constant during measurement is invalid, and this is likely to affect measurements that occur on different length or time scales³². Furthermore, Young’s and shear moduli during macroscopic measurements of biopolymer networks such as collagen networks^33,34 and intact biological tissues^35,36 become uncoupled from each other at deformations as small as a few percent. Consequently, errors can be introduced during transformation of the primary data into material properties.

The current study does not cover the whole spectrum of cellular mechanical measurement methods. Several new techniques have recently been developed to measure cell mechanical properties at high speed (10–10,000 cells per second), such as microfluidic-based methods^37,38,39,40 and the optics-based noninvasive Brillouin microscopy method^41,42. These methods potentially can provide new avenues to extend cellular mechanical studies to clinically relevant samples. However, most of these techniques do not provide a direct measurement of the Young’s modulus of cells, which makes comparison between techniques difficult.

The goal of this work was to directly compare different methods of measuring cell mechanics by probing the same type of cells with minimal biological variation, but systematic errors may arise from different instrumentation setups, which could also contribute to the observed wide spectrum of results. For example, temporal heating of the cells during cell stretching is one of the primary sources of systematic error with OS⁴³. Measurements of cell elasticity with OS can lead to shortening of the time scale at which the cells respond owing to the elevated temperature from the laser. The potential sources of systematic error for PTM^44,45, AFM^24,34,35, MTC^46,47, and parallel-plate measurements⁴⁸ have been discussed previously. Importantly, the reported systematic relative error is, in general, <20%, whereas the observed differences in measured elastic moduli with these different methods can be more than three orders of magnitude. The ~1,000-fold differences in elasticity measured by AFM and PTM in the present study were in the same range as shown in a previous study in which the mechanical properties of nontumorigenic breast epithelial MCF-10A cells and tumorigenic breast cancer MDA-MB-231 cells were measured⁴⁹. Therefore, the measurement spread between different cell mechanical assays is less likely to be due to method-dependent systematic errors, and more likely to be due to the differential mechanical responses of cells to the different force profiles produced by these different methods.

Methods

Cell culture

MCF-7 cells (American Type Cell Culture, Manassas, VA) were cultured at 37 °C and 5% CO₂ in culture medium consisting of DMEM supplemented with 10% FBS and penicillin–streptomycin. Cell lines were passaged every 3–4 d according to their growing conditions.

Parallel plates

Each MCF-7 cell was subjected, successively, to three different protocols: dynamic moduli measurements, a relaxation experiment, and a creep experiment. Each measurement was separated by a lag time of 1 min; the whole protocol lasted just 6 min to limit the evolution of cell behavior in response to mechanical solicitations. We applied stresses of about 80 Pa and strains of around 10% in amplitude to ensure linear mechanical behavior of the cells (when the mechanical stress induced by the applied strain increases linearly with strain amplitude)^48,50. In dynamic rheometry, single cells were deformed sinusoidally and the storage and loss moduli were retrieved as functions of the frequency f (obtained from measurements of the ratio |δ|/|D| and the phase lag between δ(t) and D(t) for 0.01 Hz < f < 10 Hz, where δ(t) and D(t) are the instantaneous deflection of the flexible plate and the rigid plate displacement, respectively). The complex viscoelastic modulus,

$${E}^{* }=\frac{{\rm{\sigma }}}{{\rm{\varepsilon }}}=\frac{k{L}_{0}}{S}\left(\frac{{D}_{0}}{{d}_{0}}{e}^{-i{{\varphi }}}-1\right)$$

and the storage and loss moduli are therefore respectively

$$\begin{array}{c}{E}^{^{\prime} }=\frac{k{L}_{0}}{S}\left(\frac{{D}_{0}}{{d}_{0}}\cos{{\varphi }}-1\right)\\ {E}^{^{\prime\prime} }=-\frac{k{L}_{0}}{S}\left(\frac{{D}_{0}}{{d}_{0}}\sin{{\varphi }}\right)\end{array}$$

where σ and ε are the stress and strain, respectively; k is the bending stiffness; L₀ is the cell’s initial length; S is the area of contact; D₀ and d₀ are the amplitudes of the imposed sinusoidal displacement D, resulting in the movement of the plate tip d; and φ is the phase lag between D and d.

In relaxation experiments, cells were subjected to a constant strain (constant D), and we measured δ(t). The relaxation modulus $E(t)={\rm{\sigma }}(t){{\rm{/\varepsilon }}}_{0}$ then is

$$E\left(t\right)=\frac{kD\left(t\right)}{{{\rm{\varepsilon }}}_{0}S}=\frac{k{L}_{0}D\left(t\right)}{{\Delta }_{0}S}$$

The rigid plate tip is moved over a distance Δ₀ corresponding to the desired cell elongation (phase of strain increase), and a feedback loop applies a displacement D(t) to the base of the flexible plate to keep its tip in a fixed position (flexible plate deflection, and thus stress, increases to elongate the cell from its initial shape to the target elongation). The cell response is a power law of time (Supplementary Fig. 1b). Data can be fit with the expression

$$\left(t\right)=\frac{{\rm{\sin }}(\pi \alpha )}{A\pi \alpha \tau (1-\alpha )}\left[{t}^{1-\alpha }-{\left(t-\tau \right)}^{1-\alpha }\right]$$

where τ is the rise time during which strain is established (first phase of the experiment), and A and α are, respectively, the prefactor and exponent as defined in power law creep.

In creep experiments, single cells were stretched under constant applied stress. We thus applied a constant deflection δ on the flexible plate and measured the displacement D(t) of the rigid plate, which was proportional to cell elongation. The cell creep function is

$$J\left(t\right)=\frac{{\rm{\varepsilon }}(t)}{{{\rm{\sigma }}}_{0}}=\frac{D\left(t\right)S}{k{d}_{0}{L}_{0}}$$

Consistent with dynamical measurements in the frequency domain (described above), the creep function of cells follows a power law of time (Supplementary Fig. 1a), and data can be fit to $J\left(t\right)=A{t}^{\alpha }$. The exponent α is the same as the one retrieved from dynamic measurements (described above), and the prefactors A (creep) and ${E}_{0}=\sqrt{{\left({E}_{0}^{^{\prime} }\right)}^{2}+{\left({E}_{0}^{^{\prime\prime} }\right)}^{2}}$ (dynamic rheology) are related by the relationship

$${E}_{0}=\frac{{\left(2\pi \right)}^{\alpha }}{A{\rm{\Gamma }}\left(1+\alpha \right)}$$

where Γ is the gamma function, Γ(n) = (n−1)!. More technical details about the instrument itself can be found in ref.⁵¹.

Optical stretching

We used a microfluidic delivery system to serially trap and then stretch cells along the laser beam axis. We used a CCD (charge-coupled device) camera to image the elongation dynamics of the cell body caused by stretching, and then used the video to measure the time-dependent strain (Fig. 3e). We normalized the time-dependent strain extracted from the video images by the applied peak stress and a geometric factor⁵² to obtain the creep compliance for each cell. For each passage, the number of cells per OS experiment was n ≥ 55. Compliance data are presented as mean ± s.e.m. Overall, the number of individual cells analyzed was 514. Curve-fitting of the average compliance was done with the curve-fitting toolbox in Matlab (Mathworks, Natick, MA, USA). To fit the compliance of individual cells, we used a custom code to implement nonlinear least-squares fitting based on the Matlab function fminsearch (Nelder–Mead algorithm).

Cell monolayer rheology

To characterize the rheology of MCF-7 breast cancer cells, we used oscillatory shear to determine viscous and elastic cell moduli. Here we imposed either strain or stress and measured the other. We also performed creep measurements at constant shear stress to determine the creep compliance. We recorded the cell shear deformation while increasing or decreasing stress at a constant rate.

• (1) Amplitude sweep: an oscillatory excitation at a fixed frequency with stepwise increasing amplitude of either strain or stress (Fig. 4b). This protocol probes the amplitude dependence of the mechanical properties of MCF-7 cells. Here we oscillated at a frequency of 0.5 Hz and probed a strain γ between 0.001 and 0.1, which corresponds to 0.015–0.5 μm of displacement of the rheometer plates (gap between plates: 15 μm). First, we performed strain-controlled measurements and recorded the amount of stress that occurred in response. For stress-controlled measurements we remained within the observed bounds, which were typically a few hundred pascals per cell. This maintained the cell strain as a response to the applied stress at a reasonable magnitude, thus allowing us to avoid cell detachment or yielding.

• (2) Frequency sweep: the amplitude of oscillation was kept constant at a value of 0.02 for strain-controlled measurements, or at the corresponding stress value (Fig. 4c). We increased the oscillation frequency gradually from 0.1 to 10 Hz.

• (3) Creep experiments: for applied stress, the cell strain was recorded as a function of time. During measurements, each stress was kept constant for 10 s and subsequently increased stepwise. The resulting creep compliances (resulting shear divided by applied stress) were plotted as a function of time for a total of ten stress values. The curves were well approximated by a power law yielding exponents that decreased with increased stress, from approximately 0.1 to 0.01 (Fig. 4d).

• (4) Stress ramp: the applied stress was increased at a constant rate until it reached a maximum stress, and then it was decreased at the same rate back to zero (Fig. 4e). The time course of the resulting strain was recorded. We carried out this process three additional times, each time with an increased rate.

Magnetic twisting cytometry

Ferromagnetic beads (Fe₃O₄; ~4.5 μm in diameter) were coated with Arg-Gly-Asp (RGD) peptide, where 50 µg of RGD peptide per milligram of beads was incubated overnight at 4 °C in 1 ml of carbonate buffer, pH 9.4, on a tube rotator that was constantly being rotated^53,54. Beads were first added to the cell-culture dish and incubated for 10 min before the experiment. Beads were then magnetized with a strong magnetic impulse (~1,000 G, <100 μs), giving rise to the bead’s magnetic moment. A sinusoidal varying magnetic field (0.3 Hz) perpendicular to that of the bead’s magnetic moment was then applied to rotate the bead. We used the MTC technique of measuring cell stiffness^{53,54,55,56,57} to exert an oscillatory force on the cells with a peak stress of 17.5 Pa by varying the magnetic twisting field between 0 and 50 G. By quantifying the magnetic bead displacements, we were able to calculate the cell stiffness in units of pascals per nanometer, the bead embedded area, and the cell complex modulus^55,58.

The complex shear modulus (G) is defined as

$$G=G^{\prime} +iG^{\prime\prime}$$

where the real part (G′) is the storage modulus, the imaginary part (Gʺ) is the loss modulus, and i is the unit imaginary number $\sqrt{-1}$. The component of the bead displacement that is in phase with the applied magnetic torque corresponds to G′ and is a measure of stiffness. G′ is proportional to the stored mechanical energy. The component of the bead displacement that is out of phase with the magnetic torque corresponds to Gʺ and is a measure of friction. Gʺ may be taken as the dissipated mechanical energy. Because MTC applies a rotational shear stress, the Young’s modulus is calculated with the assumption that the cell is incompressible, and it is three times the shear modulus. During twisting, the applied apparent stress (σ) is

$${\rm{\sigma }}=cH\cos{\rm{\alpha }}$$

where $(\pi {\rm{/}}2)-{\rm{\alpha }}$ is the angle of the bead’s magnetic moment relative to the twisting field, c is the bead constant (in pascals per gauss), and H is the applied magnetic field (in gauss). To calibrate the bead constant, we placed beads in a fluid of known viscosity. Throughout this study, beads with a constant of 0.35 Pa/G were used. The actual stress (σ*) depends on the contact area between the bead and the cell surface, and thus σ* = βσ, where β is determined from the bead-embedded area by finite element analysis⁵⁸. The cell stiffness is calculated as $G=\sigma * {\rm{/}}\varepsilon$, where ε is the angular strain that equals the displacement of the bead divided by the radius of the bead.

Ballistic-injection nanorheology or particle-tracking microrheology

MCF-7 cells were plated on a 35-mm dish (Corning) and reached ~90% confluence before ballistic injection. 100-nm-diameter fluorescent polystyrene nanoparticles (Invitrogen) were ballistically injected into the cells with a Biolistic PDS-1000/HE particle-delivery system (Bio-Rad, Richmond, CA). Nanoparticles were coated on microcarriers (Bio-Rad) and allowed to dry for 6 h before injection. 1,100-p.s.i. rupture disks (Bio-Rad) were used to apply pressure to accelerate nanoparticles. Cells were repeatedly washed with Hank’s Balanced Salt Solution (Gibco) after ballistic bombardment to eliminate excess nanoparticles, thus reducing endocytosis of nanoparticles. Cells were allowed to recover in fresh growth medium overnight before embedded nanoparticles were tracked with a high-magnification objective (60×/1.4-NA (numerical aperture) Plan Apo lens; Nikon, Melville, NY). We verified that none of the probed nanoparticles underwent directed motion. An optimized region of interest was generated with NIS-Elements software. Movies of the Brownian motion of the fluorescent nanoparticles were captured at 30 frames per second for 20 s with an electron-multiplying charge-coupled device (EMCCD) camera (Andor Technology, Belfast, Ireland) mounted on a Nikon TE2000 microscope. Particle trajectories were tracked and analyzed with customized Matlab software (MathWorks, Natick, MA, USA). At least 200 different nanoparticles were tracked per condition. Three biological repeats were conducted.

Cells were incubated overnight before imaging after injection. Because injected nanoparticles can uniformly disperse throughout the entire cytoplasm in cells, the differences detected represent global changes in cytoskeletal stiffness as opposed to location-specific cytoskeletal changes. The MSDs (Δr²) of individual nanoparticles are calculated from 600-frame (20-s)-long streams of the centroid locations of the nanoparticles¹⁸. The mean elasticity of the cytoplasm is calculated from the ensemble-averaged MSD through the following steps as described by Mason et al.⁵⁹. Briefly, the ensemble-averaged MSD of the nanoparticles is related to the complex viscoelastic modulus as follows¹⁹:

$${G}^{* }\left({\rm{\omega }}\right)=\frac{{k}_{{\rm{B}}}T}{{\rm{\pi }}ai\omega \,{\Im }_{u}\left\{\langle\Delta {r}^{2}\left(\tau \right)\rangle\right\}}$$

where k_B is Boltzmann’s constant, T is the absolute temperature of the cell (in Kelvin), a is the radius of the nanoparticles, $\omega =1{\rm{/}}\tau$, τ is the time lag, and ${\Im }_{u}\left\{\left\langle \Delta {r}^{2}\left(\tau \right)\right\rangle \right\}$ is the Fourier transform of $\left\langle \Delta {r}^{2}\left(\tau \right)\right\rangle$, the time-lag-dependent, ensemble-averaged MSD. The above equation can be solved analytically⁶⁰, which allows the frequency-dependent elastic modulus to be calculated algebraically using the relationship

$${G}^{^{\prime} }\left(\omega \right)=\left|{G}^{* }\left(\omega \right)\right|{\rm{\cos }}\left(\frac{{\rm{\pi }}a\left(\omega \right)}{2}\right)$$

where

$$\left|{G}^{* }\left(\omega \right)\right|=\frac{2{k}_{{\rm{B}}}T}{3{\rm{\pi }}a\left\langle \Delta {r}^{2}\left(1{\rm{/}}\omega \right)\right\rangle {\rm{\Gamma }}\left(1+\alpha \left(\omega \right)\right)}$$

Here, α is the local logarithmic slope of $\left\langle \Delta {r}^{2}\left(1/\omega \right)\right\rangle$ at the frequency of interest and Γ is the gamma function. The elastic modulus, ${G}^{^{\prime} }$, describes the propensity of a complex fluid to store energy.

Atomic force microscopy

Conical tip

AFM was conducted with a DAFM-2X Bioscope (Veeco, Woodbury, NY) mounted on an Axiovert 100 microscope (Zeiss, Thornwood, NY) using triangular silicon nitride cantilevers with a conical tip (Veeco; model DNP-10) for indentation over the cell lamella (as opposed to the cell nucleus). The indentation was carried out at a 1-Hz loading rate and a ramp size of 3 μm. The spring constant of the cantilever, calibrated by resonance measurements, was typically 0.06 N m^–1. To quantify cellular stiffness, we collected about 80 force–distance curves from 18 cells in four different samples and analyzed them according to the Hertz model modified for a conical probe,

$$F=\frac{2}{{\rm{\pi }}}\frac{E{d}^{2}\tan\theta }{\left(1-{\nu }^{2}\right)}$$

where F is the indentation force, d is the indentation distance, θ is the half-angle of the cone, ν is the Poisson’s ratio of the sample, and E is the Young’s modulus of the sample.

Sharp tip

The cells were plated on a 50-mm optical dish (Fluorodish; World Precision Instruments, Sarasota, FL) 48 h before experiments. AFM nanoindentation was performed with an MFP3D-BIO atomic force microscope (Asylum Research, Santa Barbara, CA) mounted on an IX-71 inverted optical microscope (Olympus America, Center Valley, PA) equipped with an iXon⁺ EMCCD camera (Andor Technology, Belfast, Northern Ireland). We indented the cells with an MLCT probe (Bruker, Santa Barbara, CA) that has a soft (nominal spring constant k = 0.01 N m^–1) Si_xN_y cantilever with a sharp (nominal radius r = 10 nm) Si_xN_y tip. Measurements were performed in the growth medium at 37 °C. Each cell was indented at two locations: one location over the nuclear region, and one location over the cytoplasm (lamella). These locations were selected to ensure that the region was relatively flat and not too close to any neighboring cells. At each location, the cell was indented ten times, with 1 min between each indentation. The loading rate was 2 µm s^–1 and the trigger force (the applied force at which the probe is retracted) was 600 pN.

The same experiment was conducted with an intermediate-sized LRCH-750 probe (Nanoscience Instruments, Phoenix, AZ) (r = 680 nm; k = 0.214 N m^–1) wherein cells were indented 3–4 times over only the nuclear region. The loading rate was 2 µm s^–1 and the trigger force—the applied force at which the probe is retracted—was 8.5 nN.

Data-processing method

For all force–indentation curves, we corrected the virtual deflection by fitting a line through the noncontact region and subtracting the force value of the fit line from the force value of the curve at every (F, d) coordinate. Contact points were determined and any pathological curves were filtered by visual inspection. The contact region of each curve was separated into 100-nm segments starting at the contact point. Each segment was then fit separately to the contact model to get the effective modulus at the corresponding depth. The geometry of the contact determines the power law exponent and prefactors relating the (F, d) data to the elastic modulus. Segments are linearized to the model and then least-squares linear regression is performed to find the best value of the modulus. For the conical-indenter model,

$$F=\frac{2}{{\rm{\pi }}}\frac{E{d}^{2}\tan\theta }{\left(1-{\nu }^{2}\right)}$$

where F is the indentation force, d is the indentation distance, θ is the half-angle of the cone, ν is the Poisson’s ratio of the sample, and E is the Young’s modulus of the sample. The intermediate-sized LRCH-750 tips were fit with a blunted cone model introduced by Briscoe et al.⁷,

$$\begin{array}{l}F=\frac{2E}{\left(1-{{\rm{\nu }}}^{2}\right)}\left\{ad-\frac{{a}^{2}}{2\tan\theta }\left[\frac{{\rm{\pi }}}{2}-{\sin}^{-1}\left(\frac{R\cos\theta }{a}\right)\right]\right.\\ \left.-\frac{{a}^{3}}{3R}+{\left({a}^{2}-R\cos{\theta }^{2}\right)}^{1/2}\left(\frac{R\cos\theta }{2\tan\theta }+\frac{{a}^{2}-R\cos{\theta }^{2}}{3R}\right)\right\}\\ d+\frac{a}{R}\left[{\left({a}^{2}-R\cos{\theta }^{2}\right)}^{1/2}-a\right]\\ -\frac{a}{\tan\theta }\left[\frac{{\rm{\pi }}}{2}-{\sin}^{-1}\left(\frac{R\cos\theta }{a}\right)\right]=0\end{array}$$

where R is the apex radius of the tip and a is the contact radius the probe forms with the sample. The latter equation is numerically solved for a given d, and the former is approximated by a power-law equation over the defined segment. The segment is linearized by the approximate power law and fit in the same manner as the conical-indenter model.

Spherical probe

We used a Bioscope catalyst (Bruker/Veeco) atomic force microscope placed on a Nikon U2000 confocal Eclipse C1 microscope, and a standard cantilever holder cell for operation in liquids. To record force curves over the cell surface and simultaneously record cell topography, we used the force–volume mode of operation. This is important because the mechanical (Hertz) models used to derive the Young’s modulus have been developed for an indenter deforming a surface of known (spherical) geometry. Thus, we processed force curves collected only near the top of the cell, which can typically be approximated as a spherical surface. The force curves were collected with the vertical ramp size within 5–6 µm to ensure that the AFM probe detaches from the cell after each retraction. The AFM probe moves up and down during the force collection with a frequency of 1 Hz to reasonably minimize viscoelastic effects while keeping the total measurement time relatively short. It is impossible to avoid viscoelastic effects completely, and to be consistent, we performed all measurements with the same ramping speed. The force–volume images of cells were collected with a resolution of 16 × 16 pixels (typically within a 50 × 50 µm² area). A relatively flat (as described above; <10–15° of inclination angle with respect to the cell topmost point) area around the top (nucleus region of the cell) was identified. It gave about ten force curves per cell. The global position of the AFM probe at the beginning of the scanning was controlled by the optical microscope. The measurement methodology can be found in refs ^28,61.

An NPoint closed-loop scanner (200 × 200 × 30 μm, XYZ) was used in this study. A large vertical closed-loop Z-range was particularly important because the cell height was >10 μm. A closed loop is important for quantitative description of the force curves with such an extended scan range.

AFM probe: spherical indenter

A V-shaped standard narrow 200-µm AFM tipless cantilever (Veeco, Santa Barbara, CA) was used throughout the study. A 4.5–5-µm-diameter silica ball (Bangs Labs, Inc.) was glued to the cantilever as described in ref. ⁶². We measured the radius of the probe by imaging the inverse grid (TGT1 by NT-NGT, Russia). The cantilever spring constant was measured via the thermal tuning method before the spherical probe was glued.

Data-processing method

The force curves were processed through the cell–brush model^28,63. Briefly, the cell is considered in this model as a homogeneous isotropic medium covered with entropic brush⁶⁴. Consequently, during cell deformation, the AFM probe squeezes the brush, which in turn deforms the cell body. Deflection of the cantilever d results from mechanical deformation of the substrate and long-range force. The loading force F is estimated on the basis of Hooke’s law, F = kd, where k is the spring constant of the cantilever. The presented geometry implies the following relation between the parameters:

$$h=Z-{Z}_{0}+i+d$$

(1)

Here, Z is the vertical position of the cantilever, Z₀ is the value when Z is at a nondeformed position of the sample, i is the deformation of the substrate at the point of contact, and h is the separation between the AFM probe and the substrate. Z is assigned with Z = 0 at the maximum allowable deflection d_max.

AFM allows users to directly collect the parameters Z and d (so-called raw data). For the case of an AFM probe with well-defined geometry (e.g., a spherical probe) and a homogeneous isotropic material, we can use a particular case of the Hertzian model⁵², which implies that

$$i={\left[\frac{9}{16}\frac{kd}{E}\sqrt{\frac{R+{R}_{{\rm{s}}}}{R{R}_{{\rm{s}}}}}\right]}^{2/3}$$

(2)

where R_s is the radius of curvature of the substrate at the point of contact. Poisson’s ratio was chosen to be equal to 0.5 for simplicity.

Using equations (1) and (2), one can write the following formula for each specific point of contact i:

$$h=Z-Z+{\left[\frac{9}{16}\frac{kd}{E}\sqrt{\frac{R+{R}_{{\rm{s}}}}{R{R}_{{\rm{s}}}}}\right]}^{2/3}+d$$

(3)

This approach allows us to unambiguously derive the brush forces due to the adsorbed molecules, as well as the Young’s modulus of the substrate. Specifically, it is done in two steps. First, the Young’s modulus E of the substrate is found, assuming h = 0 at the moment of maximum load. Using equation (3), one can arrive at

$$\begin{array}{l}E=\frac{9}{16}k\sqrt{\frac{R+{R}_{{\rm{s}}}}{R{R}_{{\rm{s}}}}}{\left(\frac{{d}_{\max}^{2/3}-{d}^{2/3}}{Z-{d}_{\max}+d}\right)}^{2/3}\\ \approx \frac{3}{8}\sqrt{\frac{2}{3}}k{d}_{\max}^{-1/2}\sqrt{\frac{R+{R}_{{\rm{s}}}}{R{R}_{{\rm{s}}}}}{\left(\frac{{d}_{\max}-d}{Z-{d}_{\max}+d}\right)}^{3/2}{| }_{d\to {d}_{\max}}\end{array}$$

(4)

After that, one can find the force due to brush of the adsorbed molecules by the following equation:

$$h(d)=Z-{\left(\frac{9}{16}\frac{k}{E}\sqrt{\frac{R+{R}_{{\rm{s}}}}{R{R}_{{\rm{s}}}}}\right)}^{2/3}\left({d}_{\max}^{2/3}-{d}^{2/3}\right)-\left({d}_{\max}-d\right)$$

(5)

where F = kd.

By modeling the force on the adsorbed molecules with the help of the entropic brush formula, one can find the length of the molecular brush L and grafting density N as follows⁶⁴:

$${F}_{{\rm{steric}}}\approx 50{k}_{{\rm{B}}}T\frac{R{R}_{{\rm{s}}}}{R+{R}_{{\rm{s}}}}{N}^{3/2}\exp\left(\frac{-2\pi h}{L}\right)L$$

(6)

Here we assumed a finite radius of the surface asperity R_s. As before, this formula is a good approximation for 0.2 < h/L < 0.8. A nonlinear curve fitting of equations (4)–(6) allows one to derive both the Young’s modulus of the cell body and parameters of the brush (length and grafting density).

Statistics

For AFM measurement, 20 and 60 cells were measured with a conical probe at 25 °C and 6 μm s^–1 and at 37 °C and 2 μm s^–1, respectively. With spherical probes, 30, 10, and 20 cells were measured at 37 °C and 2 μm s^–1 with the 750-nm-radius probe, 25 °C and 6 μm s^–1 with the 2,500-nm-radius probe, and 37 °C and 10 μm s^–1 with the 2,500-nm-radius probe, respectively. For the parallel plates, 18 different cells were measured. For OS, 514 cells were measured. For CMR, the results were derived from eight different cell monolayers. For MTC, 193 cells were measured. For PTM, the results were derived from three different cell culture plates, and in each plate at least 20 cells were measured (with a total of ~100 beads). For Fig. 5i, a two-tailed Student’s t-test was used, with P = 0.05 used as the threshold for significance.

Reporting Summary

Further details on experimental design are available in the Nature Research Reporting Summary linked to this article.

Code availability

Custom code used in this study is available from the corresponding authors upon reasonable request.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.