Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Prediction of neural activity in connectome-constrained recurrent networks

Nature Neuroscience volume 28, pages 2561–2574 (2025)Cite this article

Subjects

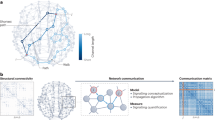
Abstract

Recent technological advances have enabled measurement of the synaptic wiring diagram, or ‘connectome’, of large neural circuits or entire brains. However, the extent to which such data constrain models of neural dynamics and function is debated. In this study, we developed a theory of connectome-constrained neural networks in which a ‘student’ network is trained to reproduce the activity of a ground truth ‘teacher’, representing a neural system for which a connectome is available. Unlike standard paradigms with unconstrained connectivity, the two networks have the same synaptic weights but different biophysical parameters, reflecting uncertainty in neuronal and synaptic properties. We found that a connectome often does not substantially constrain the dynamics of recurrent networks, illustrating the difficulty of inferring function from connectivity alone. However, recordings from a small subset of neurons can remove this degeneracy, producing dynamics in the student that agree with the teacher. Our theory demonstrates that the solution spaces of connectome-constrained and unconstrained models are qualitatively different and determines when activity in such networks can be well predicted. It can also prioritize which neurons to record to most effectively inform such predictions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Task-trained networks with the same connectivity.
Fig. 2: Predicting activity of unrecorded neurons when the activity of a subset of the network is observed.
Fig. 3: Prediction of unrecorded neuron activity depends on dimensionality, not network size.
Fig. 4: Model mismatch between teacher and student.
Fig. 5: Prediction of neural activity in networks with empirical connectome constraints.
Fig. 6: Linear teacher–student model.
Fig. 7: Loss landscape in nonlinear networks.
Fig. 8: Optimal selection of recorded neurons.

Similar content being viewed by others

Data availability

The connectomics data used in this study were published in Zarin et al.16 for Drosophila larva, in Scheffer et al.9 for the central complex of adult Drosophila and in Vishwanathan et al.41 for the brainstem of the larval zebrafish. All generated data shown in the main results, together with the teacher and student recurrent networks, are publicly available at https://doi.org/10.5281/zenodo.16618353 (ref. 65).

Code availability

All simulations and analyses were performed using custom code written in Python (https://www.python.org). The code used to generate all the results and can be found in ref. 65 and https://github.com/emebeiran/connconstr.

References

  1. Das, A. & Fiete, I. R. Systematic errors in connectivity inferred from activity in strongly recurrent networks. Nat. Neurosci. 23, 1286–1296 (2020).

    Article  CAS  PubMed  Google Scholar 

  2. Haber, A. & Schneidman, E. Learning the architectural features that predict functional similarity of neural networks. Phys. Rev. X 12, 021051 (2022).

    CAS  Google Scholar 

  3. Levina, A., Priesemann, V. & Zierenberg, J. Tackling the subsampling problem to infer collective properties from limited data. Nat. Rev. Phys. 4, 770–784 (2022).

    Article  Google Scholar 

  4. Liang, T. & Brinkman, B. A. Statistically inferred neuronal connections in subsampled neural networks strongly correlate with spike train covariances. Phys. Rev. E 109, 044404 (2024).

    Article  CAS  PubMed  Google Scholar 

  5. Dinc, F., Shai, A., Schnitzer, M. & Tanaka, H. CORNN: convex optimization of recurrent neural networks for rapid inference of neural dynamics. Adv. Neural Inf. Process. Syst. 36, 51273–51301 (2023).

    Google Scholar 

  6. White, J. G., Southgate, E., Thomson, J. N. & Brenner, S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 314, 1–340 (1986).

    Article  CAS  PubMed  Google Scholar 

  7. Ohyama, T. et al. A multilevel multimodal circuit enhances action selection in Drosophila. Nature 520, 633–639 (2015).

    Article  CAS  PubMed  Google Scholar 

  8. Zheng, Z. et al. A complete electron microscopy volume of the brain of adult Drosophila melanogaster. Cell 174, 730–743 (2018).

    Article  Google Scholar 

  9. Scheffer, L. K. et al. A connectome and analysis of the adult Drosophila central brain. eLife 9, e57443 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  10. Dorkenwald, S. et al. Neuronal wiring diagram of an adult brain. Nature 634, 124–138 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. Hildebrand, D. G. C. et al. Whole-brain serial-section electron microscopy in larval zebrafish. Nature 545, 345–349 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Turner, M. H., Mann, K. & Clandinin, T. R. The connectome predicts resting-state functional connectivity across the Drosophila brain. Curr. Biol. 31, 2386–2394 (2021).

    Article  Google Scholar 

  13. Randi, F., Sharma, A. K., Dvali, S. & Leifer, A. M. Neural signal propagation atlas of Caenorhabditis elegans. Nature 623, 406–414 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Shiu, P. K. et al. A Drosophila computational brain model reveals sensorimotor processing. Nature 634, 210–219 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  15. Pospisil, D. A. et al. The fly connectome reveals a path to the effectome. Nature 634, 201–209 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  16. Zarin, A. A., Mark, B., Cardona, A., Litwin-Kumar, A. & Doe, C. Q. A multilayer circuit architecture for the generation of distinct locomotor behaviors in Drosophila. eLife 8, e51781 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  17. Keller, A. J. et al. A disinhibitory circuit for contextual modulation in primary visual cortex. Neuron 108, 1181–1193 (2020).

    Article  Google Scholar 

  18. Kohn, J. R., Portes, J. P., Christenson, M. P., Abbott, L. F. & Behnia, R. Flexible filtering by neural inputs supports motion computation across states and stimuli. Curr. Biol. 31, 5249–5260 (2021).

    Article  Google Scholar 

  19. Lappalainen, J. K. et al. Connectome-constrained networks predict neural activity across the fly visual system. Nature 634, 1132–1140 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  20. Eckstein, N. et al. Neurotransmitter classification from electron microscopy images at synaptic sites in Drosophila melanogaster. Cell 187, 2574–2594 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Barnes, C. L., Bonnéry, D. & Cardona, A. Synaptic counts approximate synaptic contact area in Drosophila. PLoS ONE 17, e0266064 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Kasai, H., Fukuda, M., Watanabe, S., Hayashi-Takagi, A. & Noguchi, J. Structural dynamics of dendritic spines in memory and cognition. Trends Neurosci. 33, 121–129 (2010).

    Article  CAS  PubMed  Google Scholar 

  23. Bargmann, C. I. & Marder, E. From the connectome to brain function. Nat. Methods 10, 483–490 (2013).

    Article  CAS  PubMed  Google Scholar 

  24. Marder, E. Neuromodulation of neuronal circuits: back to the future. Neuron 76, 1–11 (2012).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  25. Gutierrez, G. J., OʼLeary, T. & Marder, E. Multiple mechanisms switch an electrically coupled, synaptically inhibited neuron between competing rhythmic oscillators. Neuron 77, 845–858 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  26. Stroud, J. P., Porter, M. A., Hennequin, G. & Vogels, T. P. Motor primitives in space and time via targeted gain modulation in cortical networks. Nat. Neurosci. 21, 1774–1783 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  27. Ferguson, K. A. & Cardin, J. A. Mechanisms underlying gain modulation in the cortex. Nat. Rev. Neurosci. 21, 80–92 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  28. Connors, B. W. & Gutnick, M. J. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 13, 99–104 (1990).

    Article  CAS  PubMed  Google Scholar 

  29. Kubota, Y., Hatada, S., Kondo, S., Karube, F. & Kawaguchi, Y. Neocortical inhibitory terminals innervate dendritic spines targeted by thalamocortical afferents. J. Neurosci. 27, 1139–1150 (2007).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  30. Perich, M. G. et al. Inferring brain-wide interactions using data-constrained recurrent neural network models. Preprint at bioRxiv https://doi.org/10.1101/2020.12.18.423348 (2021).

  31. Seung, H. S., Sompolinsky, H. & Tishby, N. Statistical mechanics of learning from examples. Phys. Rev. A 45, 6056 (1992).

    Article  CAS  PubMed  Google Scholar 

  32. Saad, D. & Solla, S. A. Exact solution for on-line learning in multilayer neural networks. Phys. Rev. Lett. 74, 4337 (1995).

    Article  CAS  PubMed  Google Scholar 

  33. Gao, P. et al. A theory of multineuronal dimensionality, dynamics and measurement. Preprint at bioRxiv https://doi.org/10.1101/214262 (2017).

  34. Kim, C. M., Finkelstein, A., Chow, C. C., Svoboda, K. & Darshan, R. Distributing task-related neural activity across a cortical network through task-independent connections. Nat. Commun. 14, 2851 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  35. Russo, A. A. et al. Motor cortex embeds muscle-like commands in an untangled population response. Neuron 97, 953 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  36. Beiran, M., Dubreuil, A., Valente, A., Mastrogiuseppe, F. & Ostojic, S. Shaping dynamics with multiple populations in low-rank recurrent networks. Neural Comput. 33, 1572–1615 (2021).

    Article  PubMed  Google Scholar 

  37. Sompolinsky, H., Crisanti, A. & Sommers, H. J. Chaos in random neural networks. Phys. Rev. Lett. 61, 259 (1988).

    Article  CAS  PubMed  Google Scholar 

  38. Clark, D. G., Abbott, L. F. & Litwin-Kumar, A. Dimension of activity in random neural networks. Phys. Rev. Lett. 131, 118401 (2023).

    Article  CAS  PubMed  Google Scholar 

  39. Hamood, A. W. & Marder, E. Animal-to-animal variability in neuromodulation and circuit function. Cold Spring Harb. Symp. Quant. Biol. 79, 21–28 (2014).

    Article  PubMed  Google Scholar 

  40. Turner-Evans, D. B. et al. The neuroanatomical ultrastructure and function of a biological ring attractor. Neuron 109, 1582 (2021).

    Article  CAS  PubMed  Google Scholar 

  41. Vishwanathan, A. et al. Predicting modular functions and neural coding of behavior from a synaptic wiring diagram. Nat. Neurosci. 27, 2443–2454 (2024).

  42. Kim, S. S., Rouault, H., Druckmann, S. & Jayaraman, V. Ring attractor dynamics in the Drosophila central brain. Science 356, 849–853 (2017).

    Article  CAS  PubMed  Google Scholar 

  43. Noorman, M., Hulse, B. K., Jayaraman, V., Romani, S., Hermundstad, A. M. Maintaining and updating accurate internal representations of continuous variables with a handful of neurons. Nat. Neurosci. 27, 2207–2217 (2024).

  44. Ben-Yishai, R., Bar-Or, R. L. & Sompolinsky, H. Theory of orientation tuning in visual cortex. Proc. Natl Acad. Sci. USA 92, 3844–3848 (1995).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  45. Prinz, A. A., Bucher, D. & Marder, E. Similar network activity from disparate circuit parameters. Nat. Neurosci. 7, 1345–1352 (2004).

    Article  CAS  PubMed  Google Scholar 

  46. Mastrogiuseppe, F. & Ostojic, S. Linking connectivity, dynamics, and computations in low-rank recurrent neural networks. Neuron 99, 609–623 (2018).

    Article  CAS  PubMed  Google Scholar 

  47. Dubreuil, A., Valente, A., Beiran, M., Mastrogiuseppe, F. & Ostojic, S. The role of population structure in computations through neural dynamics. Nat. Neurosci. 25, 783–794 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  48. Singer, W. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 55, 349–374 (1993).

    Article  CAS  PubMed  Google Scholar 

  49. Koch, C. & Segev, I. The role of single neurons in information processing. Nat. Neurosci. 3, 1171–1177 (2000).

    Article  CAS  PubMed  Google Scholar 

  50. Goaillard, J.-M. & Marder, E. Ion channel degeneracy, variability, and covariation in neuron and circuit resilience. Annu. Rev. Neurosci. 44, 335–357 (2021).

    Article  CAS  PubMed  Google Scholar 

  51. Seung, H. S. Predicting visual function by interpreting a neuronal wiring diagram. Nature 634, 113–123 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  52. Li, H., Xu, Z., Taylor, G., Studer, C. & Goldstein, T. Visualizing the loss landscape of neural nets. Adv. Neural Inf. Process. Syst. 31, 6391–6401 (2018).

    Google Scholar 

  53. Fort, S. & Jastrzebski, S. Large scale structure of neural network loss landscapes. Adv. Neural Inf. Process. Syst. 32, 6709–6717 (2019).

    Google Scholar 

  54. Simsek, B. et al. Geometry of the loss landscape in overparameterized neural networks: symmetries and invariances. In Proceedings of the International Conference on Machine Learning 9722–9732 (PMLR, 2021).

  55. Gutenkunst, R. N. et al. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 3, e189 (2007).

    Article  PubMed  PubMed Central  Google Scholar 

  56. Daniels, B. C., Chen, Y. J., Sethna, J. P., Gutenkunst, R. N. & Myers, C. R. Sloppiness, robustness, and evolvability in systems biology. Curr. Opin. Biotechnol. 19, 389–395 (2008).

    Article  CAS  PubMed  Google Scholar 

  57. Fisher, D., Olasagasti, I., Tank, D. W., Aksay, E. R. & Goldman, M. S. A modeling framework for deriving the structural and functional architecture of a short-term memory microcircuit. Neuron 79, 987–1000 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  58. Naumann, E. A. et al. From whole-brain data to functional circuit models: the zebrafish optomotor response. Cell 167, 947–960 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  59. Otopalik, A. G. et al. Sloppy morphological tuning in identified neurons of the crustacean stomatogastric ganglion. eLife 6, e22352 (2017).

  60. O’Leary, T., Sutton, A. C. & Marder, E. Computational models in the age of large datasets. Curr. Opin. Neurobiol. 32, 87–94 (2015).

    Article  PubMed  PubMed Central  Google Scholar 

  61. Werbos, P. J. Backpropagation through time: what it does and how to do it. Proc. IEEE 78, 1550–1560 (1990).

    Article  Google Scholar 

  62. Kingma, D. P. & Ba, J. L. Adam: a method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR, 2015).

  63. Paszke, A. et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 32, 8026–8037 (2019).

    Google Scholar 

  64. Van Overschee, D. P. & De Moor, B. Subspace Identification for Linear Systems: Theory–Implementation–Applications (Springer Science and Business Media, 2012).

  65. Beiran, M. & Litwin-Kumar, A. Dataset and code for generating the figures of publication Beiran, M., Litwin-Kumar A., Prediction of neural activity in connectome-constrained recurrent networks. Zenodo https://doi.org/10.5281/zenodo.16618353 (2025).

Download references

Acknowledgements

We are grateful to L. F. Abbott for helpful discussions and comments on the paper. M.B. and A.L.-K. were supported by the Kavli Foundation, the Gatsby Charitable Foundation (GAT3708), the Burroughs Wellcome Foundation and National Institutes of Health awards R01EB029858 and RF1DA060772. A.L.-K. was supported by the McKnight Endowment Fund. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the paper.

Author information

Authors and Affiliations

  1. Zuckerman Mind Brain Behavior Institute, Columbia University, New York, NY, USA

    Manuel Beiran & Ashok Litwin-Kumar

  2. Kavli Institute for Brain Science, Columbia University Irving Medical Center, New York, NY, USA

    Manuel Beiran & Ashok Litwin-Kumar

  3. Department of Neuroscience, Vagelos College of Physicians and Surgeons, Columbia University Irving Medical Center, New York, NY, USA

    Ashok Litwin-Kumar

Authors
  1. Manuel Beiran
    View author publications

    Search author on:PubMed Google Scholar

  2. Ashok Litwin-Kumar
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.B. and A.L.-K. conceived the study. M.B. performed simulations and analyses, with contributions from A.L.-K. M.B. and A.L.-K. wrote the paper.

Corresponding authors

Correspondence to Manuel Beiran or Ashok Litwin-Kumar.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Neuroscience thanks Jakob Macke and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Related to Fig. 2.

A Teacher as in Fig. 2. The students are trained on a varying number of recorded neurons M. B Average error in the recorded and unrecorded activity between teacher and students. C Left: Error in the network activity for a given student network in a given trial, when M = 20 neurons are recorded. Right: Error in the task-related readout signal. While the recorded neurons have low error, the unrecorded neurons in the student display large deviations. D Analogous to C, when more neurons are recorded, M = 60. In this case, the activity of unrecorded neurons and the readout are well predicted. E Teacher network from panel A receives a strong external two-dimensional time-varying input, fed to a subset of 100 excitatory neurons. Middle: The dimensionality of the activity, measured by the participation ratio, increases with the input. F Error in unrecorded neuronal activity after training student networks to match the input-driven teacher (color dots), compared to the non-driven teacher (grey dots). Fewer recorded neurons are required to predict activity of unrecorded neurons in this example input-driven network. G Input-driven teacher network with different levels of connectivity sparsity and gain heterogeneity. Teachers have E-I random connectivity, and are initialized at the fixed point. A positive input of unit strength is delivered to 5 excitatory neurons. Recorded neurons correspond to excitatory neurons, while unrecorded neurons can be both excitatory or inhibitory. Teacher networks are generated with different fractions f of non-zero weights, and different ranges for the uniformly distributed gains. Both gains and biases are trained in the students. H Error in unrecorded activity after training vs number of recorded neurons, for different level of sparsity f and gain distributions. While the overall magnitude of the error changes for different gain strengths, the decay of the error as a function of M does not change.

Extended Data Fig. 2 Teacher networks with different dynamics, related to Fig. 3.

A Teachers with variable network size and fixed rank-two connectivity, generating a limit cycle. Right: Error in the activity of recorded neurons after training. The students always learn the dynamics of the teacher. B Error in the single-neuron gains after training. C Example of error in the activity of a recorded neuron and an unrecorded neuron, when there is only one recorded neuron (left), compared to when 7 neurons are recorded (right). For one recorded neuron, the student learns the frequency of the limit cycle, but the temporal profile of the unrecorded neurons does not much the profile of the teacher network. Example for N = 400. D Teachers with variable network size and random connectivity, generating chaotic dynamics. Right: Error in the activity of recorded neurons after training. The students always learn the dynamics of the teacher. E Error in the single-neuron gains for the chaotic teachers. Note that the single-neuron parameters are much better inferred given enough recorded neurons when the teacher is chaotic than when it is low-rank, because there are many more stiff dimensions. F Traces of one example neuron in teacher and student networks with size N = 400 (left) and N = 1000 (right). For N = 400, M = 64 recorded neurons is sufficient to accurately match unrecorded neural activity from the teacher (gray line), while for N = 1000, M = 64 recorded neurons is insufficient but M = 256 is sufficient.

Extended Data Fig. 3 Training connectivity with model mismatch, related to Fig. 4.

A Teacher with model mismatch in the activation function, from Fig. 4a-c. B Example traces of one recorded neuron and one unrecorded neuron in the teacher and after training the student with mismatch in the β parameter. The students networks were trained with 20 recorded neurons (left) and with 150 recorded neurons (right). C Teacher-student framework with mismatch. We train the connectivity of the student, given the teacher’s connectivity as initial condition. The single-neuron parameters are the same in teacher and student, while there is a mismatch in the activation function. Same network as in Fig. 4. D The activation function is a smooth rectification but with different degrees of smoothness, parameterized by a parameter β. Teacher RNN from Fig. 2. E Errors in the activity of recorded (left) and unrecorded (right) neurons for different values of model mismatch between teacher and student. We observe a minor decrease in the error in unrecorded neurons when recording from a large number of neurons, M ≈ 150. F Error in the recorded activity (loss function) for three different mismatch values as a function of training epochs (β = 1. means no mismatch). G Error in the unrecorded activity (loss function) for three different mismatch values as a function of training epochs. H Removing the mismatch in activation by training an additional parameter. We train a student network with the same connectivity as the teacher and different single-neuron parameters. However, the student also does not know the smoothness parameter β. The trained parameters are therefore the gains and biases of each neuron and the smoothness β. I Error in unrecorded activity after training on a subset of M recorded units, similar to C. Training the smoothness parameter of the nonlinearity provides the student with the same prediction power as students without mismatch (see Fig. 2). J Estimated parameter β during training (average and SEM over 10 different initializations). Networks do not retrieve the exact teacher value (β* = 1) although converge to values not far from it on average. Students have a bias towards estimating sharper activation functions (β > 1). Both bias and variance are reduced as the number of recorded neurons is increased.

Extended Data Fig. 4 Dimensionality of the activity and rank of connectivity in the data-constrained RNNs, related to Fig. 5.

A Neural activity traces (centered) used for training the student networks for the three different data constrained RNNs: the premotor network in the Drosophila larva, the central complex in the adult Drosophila, and the oculomotor integrator in larval zebrafish. Different trials/conditions have been concatenated. B Left: First eigenvalues of the covariance spectrum of the datasets. Right: Participation ratio of the activity covariance. The dimensionality of neural activity is higher in the premotor system, then the CX and then the premotor network, indicated by how fast the eigenvalues decay. C Left: Singular values of the connectivity matrix. Right: Estimated rank of the connectivity matrix J, calculated using the participation ratio of the distribution of singular values of J. Given the sparsity and heterogeneity in connectomes, the rank of the connectivity is high.

Supplementary information

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Beiran, M., Litwin-Kumar, A. Prediction of neural activity in connectome-constrained recurrent networks. Nat Neurosci 28, 2561–2574 (2025). https://doi.org/10.1038/s41593-025-02080-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41593-025-02080-4

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing