An improved long-term high-resolution surface pCO₂ data product for the Indian Ocean using machine learning

Abstract

Accurate estimation of surface ocean pCO₂ is crucial for understanding the ocean’s role in the global carbon cycle and its response to climate change. In this study, we employ a machine learning algorithm to correct the deviations in high-resolution (1/12°) model simulations of surface pCO₂ from the INCOIS-BIO-ROMS model (pCO₂^model) for the period 1980–2019, using available observations (pCO₂^obs). We train the XGBoost model to generate spatio-temporal deviations (pCO₂^obs − pCO₂^model) of pCO₂^model. The interannually and climatologically varying deviations are then added back to the original model separately, which results in an improved surface pCO₂ data product. A comparison of our surface pCO₂ data product with moored observations, gridded SOCAT, CMEMS-LSCE-FFNN, and OceanSODA demonstrates an improvement by approximately 40% ± 3.31% in RMSE. Further analysis reveals that adding climatological deviations to pCO₂^model results in greater improvements than adding interannual deviations. This analysis underscores the ability of machine learning algorithms to enhance the accuracy of model-simulated surface pCO₂ outputs.

Background & Summary

Since the Industrial Revolution, anthropogenic activities such as deforestation, changes in land use and cover, the manufacturing of cement, and burning fossil fuels have contributed to the rise in atmospheric carbon dioxide (CO₂)¹. Approximately 50% of the CO₂ released by human activities is absorbed by both land and water². Based on the Global Carbon Budget, 2023³, the ocean absorbed about 26% of the total CO₂ during 2013-2022.

The coasts of the Indian Ocean (IO) host close to 30% of the world’s population^4,5. As a result, these regions are subject to high anthropogenic pressure. The high freshwater influx from rivers in the north Indian Ocean, seasonal reversing currents due to the seasonal reversal of monsoonal winds, and high aerosol deposition severely affect the carbon cycle of the north Indian region^{6,7,8,9,10,11,12,13}. Further, climatic events like El Niño-Southern Oscillation (ENSO) and Indian Ocean Dipole (IOD) are observed to affect the partial pressure of the CO₂ (pCO₂) and pH variability in the IO region^14,15,16,17.

As a part of the Regional Carbon Cycle Assessment and Processes-2 (RECCAP2) project, multiple approaches, such as interpolated observational climatology, hindcast models, observation-based surface pCO₂ (empirical models), and atmospheric inversion models were utilized for estimating net air-sea CO₂ fluxes between 1985 and 2018. A high-resolution (1/12°) regional hindcast model, known as INCOIS-BIO-ROMS (IBR_Original), was configured following the RECCAP2 ocean modeling protocol for the regional oceans. The IBR_Original model simulated outputs from 1980-2019 were part of the RECCAP2 assessment process⁵ and used to study the ocean acidification over the IO region¹⁶.

Regional ocean models provide valuable insights to oceanic pCO₂ variability and trends but often exhibit significant biases due to their limitations in representing small-scale processes and associated uncertainties in model parameterizations. Although observations are essential to understand surface pCO₂ variability, the availability of spatially and temporally varying observations is limited, especially in the IO. This data scarcity poses a challenge for validating and improving observations-based model predictions. The errors between model outputs and observations can hinder our ability to accurately estimate surface pCO₂ and associated air-sea CO₂ flux, underscoring the need for advanced correction techniques that can bridge the gap between modeled and observed surface pCO₂ values.

Machine learning (ML) algorithms offer a promising method to improve the quality of model-simulated surface pCO₂ by correcting its biases^18,19 with respect to the observations. The ML algorithms are also widely applied to predict surface pCO₂ using observations^{13,20,21,22,23,24}. ML algorithms can capture complex, nonlinear relationships between target and predictor variables^{13,20– 24}. Integrating ML-based corrections with existing model outputs makes it possible to produce more reliable and high-resolution surface pCO₂ estimates that better reflect observed conditions¹⁹.

This study aims to produce an ML-based improved surface pCO₂ data product by combining the available observations and the high-resolution IBR_Original model-simulated outputs for the IO region from 1980 to 2019. This data product will be useful to estimate more accurate air-sea CO₂ flux and identify areas in the IO that act as source (releasing CO₂ into the atmosphere) and sink (absorbing CO₂ from the atmosphere) of CO₂. With improved accuracy in modeled pCO₂, we can gain a better understanding of IO acidification in response to the ever-changing climate.

Methods

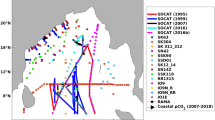
For improving model-simulated surface pCO₂ using heterogeneous in-situ observations across IO, we divided the IO region into four sub-regions (Fig. 1) as (a) the Arabian Sea (0° N–30° N; 30° E–78° E), (b) the Bay of Bengal (0° N–30° N; 78° E–110° E), (c) Central IO (0° N–18° S; 30° E–120° E) and (d) Southern IO (18° S–30° S; 30° E–120° E). This division is based on the complexity of regional physical processes in the IO region⁵.

Fig. 1

Represents the study region (Indian Ocean (IO)) and the sub-regions (Arabian Sea, Bay of Bengal, Central IO, and Southern IO). (a) Shows the yearly variations in pCO₂ observations acquired from the SOCAT (Surface Ocean CO₂ Atlas) data, and (b) is a representation of the yearly variation in observations from SAS (Sridevi and Sarma) data.

We assume that the surface pCO₂ deviant (observed pCO₂ (pCO₂^obs) - modeled pCO₂ (pCO₂^model)) is a function of surface temperature (SST), surface salinity (SSS), mixed layer depth (MLD), surface dissolved inorganic carbon (DIC), surface nitrate (NO₃), and surface chlorophyll-a (CHL). The changes in the above-mentioned ocean variables significantly control the variability of surface pCO₂. The variables SST, SSS, MLD, DIC, NO₃, and CHL are considered as the proxies of major ocean processes such as ocean thermodynamics, solubility, stratification, and biological pump. In this study, we predict the spatio-temporal varying surface pCO₂ deviants using an ML model. These predicted pCO₂ deviants are then added to the pCO₂^model to get the corrected surface pCO₂. Figure 2 is a schematic diagram showing the complete methodology adopted for this study. The details of the data required for this study, description of the ML model, and mapping methodology are described below.

Fig. 2

Schematic representation of the complete methodology adopted in this study to improve pCO₂^model.

Data Acquisition

We acquire pCO₂^obs from two different sources. The first source is the Surface Ocean CO₂ Atlas (SOCAT) (https://socat.info/index.php/version-2022/)²⁵ available for the period 1984 to 2019 in the IO. The availability of spatio-temporaral varying surface pCO₂ observations from SOCAT is shown in Fig. 1a. In addition to the SOCAT database, the surface pCO₂ observations are also collected from different Indian scientific cruises denoted as SAS (Sridevi and Sarma) data¹¹. The SAS data is available from 1991 to 2019. More details of the SAS data are available in our recent study¹³. Figure 1b shows the spatio-temporal availability of the surface pCO₂ from the SAS dataset. Data collection and quality control methods are explicitly available in the literature corresponding to each of these datasets^11,25.

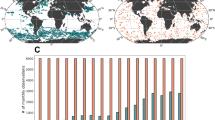
The monthly data frequency of available surface pCO₂ observations (pCO₂^obs) (SOCAT and SAS) from various sources is shown in Fig. 3 for four sub-regions of the Indian Ocean (IO), namely the Arabian Sea (AS), the Bay of Bengal (BoB), the Central IO and the Southern IO. In the AS region, a significantly higher number of observations is recorded from May to September compared to other months. Similarly, a large number of observations are available from February to May in the BoB. Observations in the AS and Central IO peak during the southwest monsoon season (June–September), while the pre-monsoon season (March–May) sees the maximum number of observations in the BoB and Southern IO regions (Fig. 3). This analysis highlights potential sources of prediction uncertainty due to data unavailability during certain periods. As the number of observations increases, the accuracy of predictions is expected to improve. Despite these temporal gaps, the data provide excellent spatial coverage across the IO region (Fig. 1).

Fig. 3

Monthly observations of pCO₂ (SOCAT+SAS) are divided into four sub-regions (a)–(d) of the Indian Ocean (IO). The blue bars denote the northeast monsoon season (December-February), while the green, yellow, and red bars represent the pre-monsoon (March-May), summer monsoon (June-September), and post-monsoon (October-November) seasons, respectively.

The input data of the ocean state variables (SST, SSS, MLD, DIC, NO₃, and CHL) are extracted from the IBR_Original model at locations at which pCO₂^obs are available from different sources (SOCAT and SAS). We also extracted the surface pCO₂ from IBR_Original i.e. pCO₂^model at these same locations. The IBR_Original model outputs are of 1/12° spatial resolution and are available from 1980 to 2019 on a monthly scale. The IBR_Original model outputs used in this study have been already validated and utilized in our previous studies^5,16. Hence, we encourage readers to refer to our previous studies^5,16 for more details on the IBR_Original model configuration.

We checked the data distribution for each sub-region of IO before using the data for training and predictions. The MLD, CHL, and NO₃ data are converted to a normal distribution by taking their log transformation. Since ML models are sensitive to outliers (>3σ), the outliers are removed from the available data for each sub-region of IO.

The Bay of Bengal Ocean Acidification (BOBOA) mooring is the only point-source observation of surface pCO₂ available from 2014-2018 in the IO region. Hence, it is used as an independent dataset for assessing improvements in surface pCO₂ at the BOBOA mooring location. The BOBOA mooring is located at 15° N, 90° E. The observation data at this location is converted to a monthly frequency before being compared with the simulated pCO₂. The surface pCO₂ data from BOBOA is downloaded from https://www.pmel.noaa.gov/co2/story/BOBOA.

We acknowledge that the scarcity of gap-free spatio-temporal observations is a common challenge in ocean carbonate variable studies. One approach for independent validation is to remove a specific cruise line from the dataset. However, this would reduce the number of available observations for developing ML models, potentially affecting their overall performance. More importantly, cruise lines are region-specific and often lack broad temporal coverage, making it unjustified to assess improvements across the entire IO based solely on validation using a single cruise line. Given that the corrected pCO₂ dataset has a high spatial resolution of 1/12° and spans from 1980 to 2019, it is essential to evaluate its improvements across the entire IO region.

The gridded SOCAT is a monthly 1° binned data product prepared from SOCAT cruise observations²⁵. The surface pCO₂ from IBR_Original has a spatial resolution of 0.083°. The pCO₂ values corresponding to each cruise location are extracted from this dataset, and the difference is used as our target variable (pCO₂ deviant). This extraction is performed using the nearest-neighbour interpolation method. Nevertheless, the SOCAT 1° data product bins values into a 1° grid without interpolation, resulting in slight differences from the values used for training. Therefore, we use the SOCAT 1° dataset to assess whether the final product demonstrates an improvement or decline in surface pCO₂ values. The pCO₂^model and corrected pCO₂ datasets have a monthly frequency, making the monthly gridded SOCAT data particularly useful for evaluating the improvement of the corrected pCO₂ datasets compared to observations. In the IO region, gridded SOCAT data is available from 1984 to 2019. This data can be downloaded from https://socat.info/index.php/data-access/.

ML-based products are important as they provide spatio-temporally gap-free estimates. In this study, we use two high-resolution (0.25° × 0.25°) gridded ML-based data products (CMEMS-LSCE-FFNN (Copernicus Marine Environment Monitoring Service–Laboratoire des Sciences du Climat et de l’Environnement feed-forward neural network)²³ and OceanSODA (OceanSODA-ETHZv2)²⁴). For this study, the CMEMS-LSCE-FFNN (OceanSODA) data is taken from 1985 (1982) to 2019. The CMEMS-LSCE-FFNN data is downloaded from https://data.ipsl.fr/catalog/srv/eng/catalog.search#/metadata/a2f0891b-763a-49e9-af1b-78ed78b16982. While the OceanSODA data is downloaded from https://zenodo.org/records/11206366. Although these data products were developed using SOCAT observations, they employ different methodologies for constructing surface pCO₂, leading to inherent differences among them. Additionally, the availability of data products with varying spatial resolutions, such as CMEMS-LSCE-FFNN and OceanSODA, enables a more rigorous comparison of our product. This comprehensive evaluation enhances confidence in the reliability of the final product. Table 1 summarizes all the data used in this study.

Table 1 Summarized information of the data used in this study.

Splitting and Scaling Data

In this study, SST, SSS, MLD, NO₃ concentration, and CHL from IBR_Original are used as predictors. The deviation between the pCO₂^obs values (from SOCAT and SAS datasets) and the pCO₂^model values [pCO₂^obs–pCO₂^model] serves as the target. The data from each of the four sub-regions are randomly divided into training (80%) and testing (20%) datasets using the Scikit-Learn module²⁶. These test datasets are kept separate for each sub-region and are exclusively used to validate the model’s performance, ensuring unbiased evaluation. To train the models and prevent the overfitting issue, a 10-fold cross-validation technique is applied. In this approach, the training dataset is split into 10 subsets (folds). The model is trained on nine of these folds and validated on the remaining one, with the process repeated for all folds.

Machine Learning Algorithm

The study utilizes an advanced ML algorithm, eXtreme Gradient Boosting (XGB), to produce an improved version of pCO₂^model for the IO region during the period 1980-2019. The details of the XGBoost algorithm are given below.

• eXtreme Gradient Boosting (XGB) The XGB algorithm²⁷ is a supervised learning algorithm that belongs to the decision tree-based boosting algorithm family. The XGB algorithm was created by increasing the computational speed and performance of the gradient-boosted algorithm. Previous studies highlight the algorithm’s superior computational speed, accuracy, and overall performance compared to other machine learning algorithms^13,19,22,28. The proven capability of this advanced ML algorithm in previous studies motivates us to employ this XGB algorithm to correct the pCO₂^model for each of the four sub-regions of the IO. This algorithm starts with an initial guess, and then trees are added sequentially. Each tree tries to improve the ensemble’s performance by minimizing a loss function. In this study, the model developed using the XGB algorithm is hereafter referred to as the ‘XGB-model.’

Performance of the tuned XGB-model

The XGB-model has tunable hyper-parameters. Following previous literature^13,22, we decided to use the Optuna optimization²⁹ to tune the hyper-parameters. The hyper-parameters range, and final optimized values for each of the sub-regions are shown in Table 2. To determine whether the tuned XGB-model is neither overfitting nor underfitting, it is essential to evaluate the performance of the XGB-model using the 20% test dataset set kept aside during the 80:20 data split for each sub-region of the IO. The performance of the four individual XGB-models developed for these sub-regions is summarized in Table 3. Similar RMSE values for the training and testing datasets across the respective sub-regions indicate consistent and reliable XGB-model performance throughout all sub-regions.

Table 2 Optimized values of the XGB hyper-parameters of the model developed for each sub-region (Arabian Sea, Bay of Bengal, Central IO, and Southern IO) of the IO region.

Table 3 Train and test RMSE (μatm) values of XGB models for four (Arabian Sea, Bay of Bengal, Central IO, Southern IO) regions.

Best Estimate and Uncertainty

To quantify the uncertainty associated with predicting pCO₂ deviants, we adopt a method similar to the bootstrapping technique in statistics^21,23. This approach requires generating a large number of models, where the average prediction provides the best estimate of the target (pCO₂ deviants), and the standard deviation (SD, 1-σ) quantifies the predictive uncertainty.

To achieve this, we generate 150 training datasets for each sub-region by randomly extracting 80% of the data from the training set used during hyperparameter tuning. This process results in 150 independently trained XGB-models. Subsequently, we create ensembles of varying sizes, from a minimum of 2 to a maximum of 150 XGB-models. The optimal ensemble size, defined as the size at which the RMSE (evaluated against the test dataset) stabilizes with no significant improvement, is then identified for each sub-region. As shown in Fig. 4, the optimal ensemble size is 140 for the AS and the Central IO, while it is 130 for the BoB and the Southern IO.

Fig. 4

Evaluation of RMSE as a function of ensemble size across the four sub-regions ((a) Arabian Sea, (b) Bay of Bengal, (c) Central IO, and (d) Southern IO) to determine optimal ensemble size.

Mapping Method

To generate the spatio-temporal variation in pCO₂ deviants for each sub-region, spatio-temporal inputs (SST, SSS, MLD, DIC, NO₃ concentration, and CHL) from IBR_Original (covering the period 1980–2019) are fed into each of the 140 XGB-models (for the AS and the Central IO) or 130 XGB-models (for the BoB and the Southern IO). As mentioned in the previous section, the average output of these algorithms provides the best estimate of the spatio-temporal pCO₂ deviants, while the standard deviation quantifies the associated uncertainty for the period 1980–2019. Figure 5 shows the domain-averaged pCO₂ deviants and their corresponding uncertainties for each sub-region. These spatio-temporal pCO₂ deviants are then added back to the pCO₂^model (at each grid cell) to derive the corrected pCO₂.

Fig. 5

The figure displays the annual variation of the pCO₂ deviants for the four sub-regions. The solid line shows the best estimates for each of the sub-regions of the IO domain, and the error bar indicates the associated uncertainty.

Here, we examine two different approaches for incorporating spatial deviants into the pCO₂ correction process. In the first approach, the interannual deviants are added to the pCO₂^model, resulting in the interannually corrected pCO₂ dataset (pCIBR_Int). In the second approach, only the climatological mean of the deviants is added to the pCO₂^model, producing the climatologically corrected pCO₂ dataset (pCIBR_Clim). Since the variability of the climatological deviance is greater than that of the interannual variability, we aim to determine which approach yields better results. The data products generated using both methods are extensively validated against BOBOA moored buoy-based observations, gridded 1° × 1° SOCAT dataset, and two additional gridded data products (CMEMS-LSCE-FFNN and OceanSODA) to identify the most effective method for correcting surface pCO₂ data.

Data Records

The long-term high-resolution corrected surface pCO₂ datasets (pCIBR_Clim and pCIBR_Int) produced for the IO region can be accessed from https://zenodo.org/records/14614739³⁰. This product has a monthly temporal resolution and a spatial resolution of 1/12°. The data is available from 1980-2019. From the same link, the users can access the input data used to correct pCO₂^model and the pCO₂ deviants, along with the associated uncertainty derived from the XGB-models. All the data are provided in a single NetCDF file.

Technical Validation

A comparison of the pCO₂^model and the corrected surface pCO₂ data products (pCIBR_Int and pCIBR_Clim) has been carried out against the time series observations of surface pCO₂ from the BOBOA moored buoy location (Fig. 6). This study employs three statistical metrics (Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Taylor Skill Score (TSS)) to evaluate the performance of the corrected pCO₂ data against the pCO₂^model using the BOBOA mooring-based observations. As summarized in Table 4, the RMSE between pCIBR_Clim (pCIBR_Int) and the BOBOA pCO₂ observations decreased by approximately 37.84%  ± 2.35% (40.63%  ± 0.38%) compared to the RMSE between the pCO₂^model and BOBOA. Similarly, the MAE decreased by about 50.43%  ± 1.85% for pCIBR_Int and 44.46%  ± 5.84% for pCIBR_Clim. The TSS measures the agreement between model outputs and reference data, particularly with respect to variability, where a value close to 1 indicates a perfect match. The pCO₂^model demonstrates a good TSS of 0.87. However, the corrections applied in this study further improve the TSS by approximately 1.11%  ± 0.77% for pCIBR_Int and 2.23%  ± 0.62% for pCIBR_Clim. Based on the comparison with BOBOA observations, we conclude that both correction methods (pCIBR_Clim and pCIBR_Int) provide significant improvements to the pCO₂^model. This comparison further indicates that both the methods perform very close to each other.

Fig. 6

Comparison of pCIBR_Int, pCIBR_Clim, and pCO₂^model with observation from BOBOA buoy, located at 15°N and 90° E. The grey-shaded region represents the standard deviation in the observation data from BOBOA buoy.

Table 4 Statistical comparison of pCIBR_Int, pCIBR_Clim, and pCO₂^model.

In addition to validation at a moored buoy location, a comparison of pCIBR_Int and pCIBR_Clim data products has been carried out with the gridded SOCAT, CMEMS-LSCE-FFNN, and OceanSODA datasets to evaluate the spatial improvement in the surface pCO₂ (Figs. 7, 8, and 9). The corrected pCO₂ datasets (pCIBR_Int and pCIBR_Clim) have a resolution of 1/12°, which is finer than all the reference datasets. Therefore, we re-grid the corrected pCO₂ data to match the grid of the reference datasets using the nearest-interpolation method.

Fig. 7

The figure represents the changes in RMSE (ΔRMSE, first row), MAE (ΔMAE, second row), and TSS (ΔTSS, third row) between pCIBR_Int (first column) or pCIBR_Clim (second column) and pCO₂^model while comparing each of them to the gridded SOCAT product. Negative values (blue) in ΔRMSE and ΔMAE indicate improvement over pCO₂^model. While positive values (red) in ΔTSS represent an improvement over pCO₂^model.

Figure 7 shows the difference in RMSE between pCIBR_Int (Fig. 7a) or pCIBR_Clim (Fig. 7b) and pCO₂^model when compared with the gridded SOCAT data. Both panels (Fig. 7a and b) demonstrate a considerable reduction in RMSE across the IO domain. Specifically, the RMSE decreases by approximately 40.43%  ± 4.39% for pCIBR_Int and 38.87%  ± 4.92% for pCIBR_Clim. The second and third rows of Fig. 7 show the differences in MAE and TSS between the corrected pCO₂ outputs (from both methods) and pCO₂^model when compared to SOCAT. The reduction in MAE is more pronounced for pCIBR_Clim (≈ 40%  ± 5%) compared to pCIBR_Int (≈ 35%  ± 4%). The third row of Fig. 7, which shows TSS differences, contains fewer grid cells than the first and second rows. This is because TSS accounts for data availabilityS, and the gridded SOCAT dataset bins cruise line data into a 1° mesh, resulting in fewer cells with repeated data values. The grid cells displayed in the third row have at least three observation data points per cell. An increase in TSS of approximately 7.13%  ± 0.22% is observed for pCIBR_Int, while pCIBR_Clim shows an increase of about 5.15%  ± 0.76%. Nevertheless, the availability of a limited number of spatio-temporal varying surface pCO₂ observations makes it challenging to conclusively determine which method (pCIBR_Int or pCIBR_Clim) better improves the pCO₂^model. However, the analysis clearly indicates that both methods result in significant improvements over SSthe pCO₂^model.

CMEMS-LSCE-FFNN and OceanSODA are observation-based reconstructed data products that provide high-resolution, gap-free, spatio-temporally varying gridded surface pCO₂. Both datasets were developed using different ML methods to predict long-term changes in surface pCO₂. These data products are widely recognized by the international scientific community for their significant contributions to advancing ocean carbon cycle research and improving our understanding of how environmental changes influence air-sea CO₂ flux dynamics. Accordingly, we utilize these datasets to perform robust spatio-temporal validation, as shown in Figs. (8 and 9).

Fig. 8

The figure represents the changes in RMSE (ΔRMSE, first row), MAE (ΔMAE, second row), and TSS (ΔTSS, third row) between pCIBR_Int (first column) or pCIBR_Clim (second column) and pCO₂^model while comparing each of them to the CMEMS-LSCE-FFNN product. Negative values (blue) in ΔRMSE and ΔMAE indicate improvement over pCO₂^model. While positive values (red) in ΔTSS represent an improvement over pCO₂^model.

Fig. 9

The figure represents the changes in RMSE (ΔRMSE, first row), MAE (ΔMAE, second row), and TSS (ΔTSS, third row) between pCIBR_Int (first column) or pCIBR_Clim (second column) and pCO₂^model while comparing each of them to the OceanSODA product. Negative values (blue) in ΔRMSE and ΔMAE indicate improvement over pCO₂^model. While positive values (red) in ΔTSS represent an improvement over pCO₂^model.

Figure (8a and b) demonstrate a significant reduction in RMSE for both pCIBR_Clim and pCIBR_Int compared to the pCO₂^model. When compared against CMEMS-LSCE-FFNN, a domain-averaged RMSE decrease of approximately 29.48%  ± 4.25% is observed for pCIBR_Int, and approximately 37.06%  ± 4.46% for pCIBR_Clim, relative to pCO₂^model. Figure (8c and d) highlight the differences in MAE between the corrected pCO₂ datasets and pCO₂^model, when compared with CMEMS-LSCE-FFNN. For pCIBR_Int, small regions, particularly in the AS, show an increase in MAE. This suggests that the addition of interannually varying pCO₂ deviants to pCO₂^model can lead to a decrease in quality in certain areas. This decline is likely due to the limited temporal frequency of pCO₂ cruise observations. In contrast, for pCIBR_Clim, regions with a decline in quality are almost negligible (Fig. 8d). Over the entire IO domain, MAE decreases by approximately 32.19%  ± 4.28% for pCIBR_Int and by approximately 38.91%  ± 4.93% for pCIBR_Clim. Similarly, Figure (8e and f) show changes in TSS. For pCIBR_Int (Fig. 8e), certain regions exhibit a decrease in TSS. However, for pCIBR_Clim (Fig. 8f), TSS increases consistently across the entire domain. The domain-averaged improvement in TSS is approximately 1.35%  ± 0.09% for pCIBR_Int and significantly higher at approximately 5.01%  ± 0.21% for pCIBR_Clim. In summary, the results indicate that pCIBR_Clim significantly outperforms pCIBR_Int. It achieves greater reductions in RMSE (37.06%  ± 4.46% vs. 29.48%  ± 4.25%) and MAE (38.91%  ± 4.93% vs. 32.19%  ± 4.38%), and a higher improvement in TSS (5.01%  ± 0.21% vs. 1.35%  ± 0.09%), with fewer regions showing quality degradation. Overall, pCIBR_Clim demonstrates superior performance and consistency when compared against CMEMS-LSCE-FFNN.

Figure 9a and b) illustrate the differences in RMSE between the corrected surface pCO₂ data products (pCIBR_Int and pCIBR_Clim) and pCO₂^model when compared with OceanSODA data. A decrease in RMSE is observed across the domain for both methods. On average, the domain-wide RMSE is reduced by approximately 30.82%  ± 4.43% for pCIBR_Int and by approximately 37.73%  ± 4.75% for pCIBR_Clim. The differences in MAE are also presented in Fig. 9c and d). Similar to the comparison with CMEMS-LSCE-FFNN, the pCIBR_Int case (Fig. 9c) shows localized increases in MAE, particularly in the AS. In contrast, the MAE decreases consistently across the IO domain for the pCIBR_Clim case (Fig. 9d). On a domain-averaged basis, MAE is reduced by approximately 34.71%  ± 4.91% for pCIBR_Int and by approximately 40.94%  ± 5.14% for pCIBR_Clim. Figure 9e and f) show TSS improvements. For the pCIBR_Clim case, TSS shows consistent improvement across the IO domain. However, for pCIBR_Int, certain regions exhibit patches of deterioration. On average, the domain-wide TSS improves by approximately 3.81%  ± 0.15% for pCIBR_Clim and by approximately 1.00%  ± 0.08% for pCIBR_Int. In conclusion, when comparing the two corrected surface pCO₂ data products (pCIBR_Int and pCIBR_Clim) with reference to products such as CMEMS-LSCE-FFNN and OceanSODA, pCIBR_Clim demonstrates superior performance. It achieves greater reductions in RMSE and MAE, along with more consistent improvements in TSS, making it the more effective correction method.

Hence, based on this technical analysis, it is evident that both methods (pCIBR_Clim and pCIBR_Int) adopted in this study improve the pCO₂^model. Furthermore, when compared with other ML-based products, pCIBR_Clim demonstrates superior performance over pCIBR_Int. Nevertheless, we have made both products, i.e., one derived from pCIBR_Int and the other from pCIBR_Clim, available for users. The users can choose the one that best fits the purpose of their research. The corrected surface pCO₂ can be utilized to derive more accurate air-sea CO₂ flux estimations for the period 1980–2019 in the IO region. This long-term, high-resolution air-sea CO₂ flux data can also help identify regions with significant source and sink characteristics within the IO, thereby contributing to a better understanding of the IO’s role in the global carbon budget.