Background & Summary

Crystal structure determination is fundamental in materials science, particularly when studying previously unreported compounds. In academic contexts, X-ray diffraction is one of the most widely used techniques, with single-crystal and powder X-ray diffraction being the two most common methods1. Single-crystal X-ray diffraction allows for directly determining the three-dimensional crystal structure from a corresponding collection of diffracted data. In contrast, powder X-ray diffraction presents a challenge, as it compresses the three-dimensional information into a one-dimensional pattern2. This compression makes it more challenging to determine the crystal structure unambiguously, especially in the case of organic compounds.

Generally, a crystal structure can be described by symmetry information in the space group, cell parameters, atomic numbers, atomic coordinates, and atomic content. Therefore, determining a crystal structure from powder X-ray diffraction involves retrieving this 3D information from the 1D diffraction pattern2,3. In most cases, this task is performed using direct space approaches that treat the retrieval of 3D information as an optimization problem3. However, these methods have limitations, as the structural search space is prohibitively ample3.

Recently, some authors have explored machine learning techniques for this task. Some works study the prediction of space groups4,5,6,7, cell parameters8 and atomic coordinates9,10. Usually, most of these works employ datasets with diffractograms simulated from files in the Crystallographic Information File (CIF) format4,5,7,9. Nevertheless, in most cases, the CIF datasets are not free to download and lack structural diversity. Some examples include datasets with only inorganic compounds11 and only metal-organic frameworks12,13. In addition, although there are datasets with many crystal structures such as Crystallography Open Database (COD)14,15,16,17,18,19,20,21,22,23, Materials Project (MP)24 and Cambridge Structural Database (CSD)25, simulating a large volume of powder diffractograms can be expensive in terms of time and computational resources.

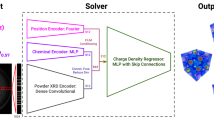
Intending to advance machine learning techniques in this field, we introduce SIMPOD, a dataset comprising 467,861 crystal structures and their corresponding simulated powder X-ray diffractograms in vector and radial-image format (Fig. 1). SIMPOD has a large variety of structures sourced from the COD14,15,16,17,18,19,20,21,22,23 up to mid-2023. COD is the open-access database that contains the most extensive collection of crystallographic structures of minerals, organic metals, organometallic structures, and small organic compounds26. Furthermore, COD is constantly growing and features crystal structures from donations by individual researchers and peer-reviewed academic press26.

Fig. 1
figure 1

Samples of (a) a simulated powder X-ray diffractogram and (b) a powder X-ray radial image.

Full size image

Based on CIF files from the entire COD14,15,16,17,18,19,20,21,22,23, we created 467,861 JSON files containing individual crystal structures and their corresponding simulated powder diffractograms. Furthermore, we generated radial images in PNG format from the powder diffractograms through a mathematical transformation described in the Methods. The latter was done to facilitate using computer vision models for this problem.

As far as we know, SIMPOD is the first public benchmark for the crystal structure determination task from powder X-ray diffraction. Its size and diversity of structures make it an appropriate dataset for training generalizable models for other essential tasks in materials science, such as crystal parameter prediction (e.g., space groups, unit cells, and atomic coordinates) and crystal structure generation, opening up new possibilities for research and discovery in the field.

Methods

Data extraction and diffractogram simulation

We used COD14,15,16,17,18,19,20,21,22,23 (https://www.crystallography.net/cod/) until August 2023, which at that date had 498,027 CIF files. We only selected crystal structures with more than 4 atoms in the asymmetric unit to focus the benchmark on structures that are more difficult to determine and up to 256 atoms due to computational cost. In addition, we used Dans Diffraction27, Gemmi28, scikit-image29, and PyAstronomy30 Python packages to filter the database and extract the structural information. Specifically, we obtained an identifier code (ID) in the original dataset, space group, cell parameters (a, b, c, α, β, γ), atom types, atomic coordinates, and atomic content of the selected structures. The structural information and corresponding diffractograms were organized and compiled into 467,861 files in JSON format.

The powder diffractograms were simulated using a 2θ range between 5° and 90°, with 10,824 total intensity points (simulating a step size around 0.008°) and default parameters from the Dans Diffraction package, that uses copper (Cu) as the source with a wavelength of 1.5406 Å and 0.01° peak width. By normalizing the diffractograms from their maximum intensity, we constrained all intensity values to be within the [0, 1] interval. These simulation parameters reflect the standard analysis conditions of a conventional diffractometer. Unlike experimental diffractograms, the simulated patterns do not include background and have fixed peak widths, which is a dataset limitation. In addition, the generated patterns correspond to a single X-ray wavelength and a flat detector. Other wavelengths, radiation types (such as neutron diffraction), and detector shapes will produce different patterns, which are not included in this dataset.

Radial images creation

We began by reducing the size of the diffractogram from 10,824 to 1,024 intensities using nearest neighbor interpolation. Following this, we applied a mathematical transformation as described below.

Let \(i\in {{\mathbb{R}}}^{d}\) be the powder diffractogram defined as i = [i1, i2, …  , id] and let x be a vector of integers ranging from  − v to v, where \(x\in {{\mathbb{R}}}^{s}\) and s = 2v + 1. This vector is defined in equation (1):

$$x=[{x}_{1},{x}_{2},\cdots \,,{x}_{s}]=[-v,-v+1,\cdots \,,-1,0,1,\cdots ,v-\,1,v]$$
(1)

Using this, we build a matrix W, where each element wa,b is a function of x as shown in equation (2). We use a constant \(k\in {\mathbb{R}}\) with k > 0 to control the scale of the values in W.

$$W=\left[\begin{array}{cccc}{w}_{0,0} & {w}_{0,1} & \cdots & {w}_{0,s}\\ {w}_{1,0} & \ddots & & \\ \vdots & & \ddots & \\ {w}_{s,0} & & & {w}_{s,s}\end{array}\right]\,\text{where}\,\,{w}_{a,b}(x)=\lfloor k\sqrt{{x}_{a}^{2}+{x}_{b}^{2}}\rceil $$
(2)

In addition, in equation (3), we define a function I that receives an input matrix and operates it element-wise.

$$I(h)=\left\{\begin{array}{l}{i}_{h}\,if\,h\in [0,d]\\ 0\,otherwise\end{array}\right.$$
(3)

From the matrix W and the function I, we can obtain an image Z = I(W − c) of dimension (s, s), where \(c\in {\mathbb{N}}\) is a constant to control the free space at the center of the image.

For this case, we set v = 260, k = 5, and c = 20. The total approximate data processing time for creating the images and diffractograms was 300 CPU hours. The source code is available at https://github.com/BCV-Uniandes/SIMPOD.git. It is important to note that the radial images could present artefacts along the horizontal and vertical axes derived from the proposed creation process.

Space Group Prediction

A simple example of SIMPOD use is training machine learning models for space group prediction. SIMPOD allows us to perform this task using simulated diffractograms and radial images. In that sense, we trained different traditional machine learning models, such as Distributed Random Forest (DRF) and Multi-Layer Perceptrons (MLP), using SIMPOD diffractograms and the H2O AutoML library31. Moreover, we trained and optimized several computer vision models, such as AlexNet32, ResNet33, DenseNet34, Swin Transformer35 and Swin Transformer V236, using the radial images and the Pytorch framework37.

The experimentation was done using 2-fold cross-validation, where each fold had 50,000 crystal structures from SIMPOD. In addition, the resulting models were tested in 25,000 crystal structures. The source code is available at https://github.com/BCV-Uniandes/SIMPOD.git. For details on training and optimization of computer vision and H2OAutoML models, see the Supplementary Information.

Experimentation results are shown in Tables 1 and 2. Complete validation results can be found in the Supplementary Information. We see that models employing radial images show the best performance, followed by the models using 1D diffractograms. Thus, we empirically demonstrate the benefits of using deep learning models trained with SIMPOD radial images for this particular task.

Table 1 Test results of H2O AutoML31 classic machine learning models trained on 1D diffractograms.
Full size table
Table 2 Test results of computer vision models trained on complete circle radial images.
Full size table

Furthermore, we observe an improvement in accuracy and top 5 accuracy in all computer vision models when complexity increases. Figure 2 presents a performance comparison for models with different complexities, highlighting a correlation between Floating Point Operations (FLOPs) per image and accuracy. Moreover, we also see that pretraining benefits model performances. Notably, the average increase in performance when using pretraining is 2.58 ± 0.83% for accuracy and 1.51 ± 0.32% for top 5 accuracy.

Fig. 2
figure 2

Model complexity measured in GFLOPs against (a) accuracy and (b) top 5 accuracy.

Full size image

As more complex and recent computer vision models demonstrate better results, researchers will benefit from using SIMPOD radial images when training state-of-the-art models. In that sense, SIMPOD represents an important benchmark for addressing different materials science tasks when using powder X-ray diffraction data.

Data Records

SIMPOD is available at Science Data Bank38. The data is organized in 2 folders containing the structural information in JSON format and the images in PNG format. Each JSON file has a dictionary with the ID, the crystallographic information, and the simulated diffractogram of a single structure. The images, named after the ID, are related to each one of the JSON files. It is paramount to mention that SIMPOD has no information about the authors or publications related to the described structures.

Technical Validation

We validated the quality and relevance of the data in five ways. First, we manually reviewed 200 random diffractograms, verifying that their 2θ values and relative intensities were consistent with the respective crystal structure. We employed the Cambridge Crystallographic Data Centre’s program Mercury39 to explore and analyze the structures. Thus, we used the simulated PXRD patterns from Mercury as the reference, verifying their similarity with the SIMPOD ones.

We observed PXRD pattern consistency in all cases, with excellent matching independent of the structure type. Some examples can be seen in Fig. 3, which shows the structure of a mineral, a coordination complex, and an organic compound together with its SIMPOD and Mercury simulated PXRD patterns, respectively. Therefore, we demonstrate the robustness of the PXRD simulation process along different crystalline compounds.

Fig. 3
figure 3

Simulated diffractograms from Mercury39 and SIMPOD, and crystal structures of (a) Searlesite (NaBSi2O5(OH)), (b) a Bipyridine Palladium Complex (C22H16F3N3OPd) and (c) methyl 5,6-diphenylpyreno[4′,5′:4,5]imidazo[2,1-a]isoquinoline-3-carboxylate (C39H24N2O2).

Full size image

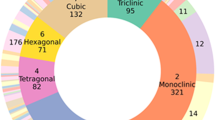
Second, we proved that the dataset has varied structural types and elemental diversity. By analyzing the distribution of atomic numbers and space groups in all SIMPOD data (Fig. 4), we found that most of them are well represented. Notably, the organic atoms, including hydrogen (H), carbon (C), nitrogen (N), and oxygen (O), are the most prevalent, with over 105 structures containing these elements in SIMPOD. This aligns with the fact that organic crystalline compounds present higher molecular diversity than their inorganic counterparts. Additionally, most elements in the periodic table have at least 103 structures and instances in the dataset, ensuring a diverse range of compositions.

Fig. 4
figure 4

Distributions of (a) atoms per structure, (b) total atoms in dataset and (c) space groups in SIMPOD and COD datasets.

Full size image

On the other hand, we saw that all the space groups are present in SIMPOD, with at least one representative structure. In fact, most space groups have more than 102 instances in SIMPOD, proving crystalline symmetry diversity. Given that COD features a variety of structural types26, it is not surprising that SIMPOD showcases significant structural and compositional diversity.

Third, we proved that COD is well represented in SIMPOD. As the selected structures are a subset of the COD, it is relevant to analyze if the structure selection process generates any structural or compositional biases. Therefore, we also analyze atomic numbers and space group distributions from COD (Fig. 4) and compare them to the SIMPOD ones. Particularly, we calculate the Kullback-Leibler Divergence (KLD) for the normalized distributions.

Taking the COD distributions as a reference, we obtained KLD values of 6.58 ⋅ 10−4 for the atomic distribution per structure, 1.35 ⋅ 10−4 for the atomic distribution in the dataset, and 9.84 ⋅ 10−3 for the space group distribution. Since the KLD for each distribution is low ( < 1 ⋅ 10−2), we demonstrate that SIMPOD is structurally and compositionally similar to COD. It is paramount to note that SIMPOD has fewer instances than COD, which could be relevant when studying less frequent structures (E.g., structures with Helium or Radon).

Fourth, we evaluated the importance of using the proposed images for model training, since we observed that image-trained models had significantly better performance than diffractogram-trained ones. Thus, we tested whether radial images with more resolution and less redundancy, such as those with only a quarter of a circle, changed performance. We created these images by replacing x with \({x}^{{\prime} }=[0,1,2,\cdots \,,2v-1,2v]\) in the process described in the Methods section.

Table 3 shows the results of Swin Transformer V236 models trained with the two versions of radial images. For additional optimization details and validation results, see the Supplementary Information. We observe that the different versions obtain similar results, showing that the image creation is valuable regardless of modality. In that sense, other image-creation approaches could also be used, and we leave exploring other processes for future research.

Table 3 Test results of Swin V236 models trained on complete and quarter of circle radial images.
Full size table

Fifth, we tested the generalization ability of the AI models trained on SIMPOD’s complete circle radial images using real experimental data. We used 20 experimental diffractograms from compounds with known crystal structures to test the implemented computer vision models. Table 4 shows the results. We hypothesize that real background affected the performance, as this element is not present in our simulated dataset. Nevertheless, it is worth noting that the best-performing model achieved a top-5 accuracy of 35% on the experimental data without an expert’s manual peak indexing or background correction. Therefore, even though SIMPOD does not contain experimental diffractograms, it still serves as a valuable benchmark for developing methods that could later be extended to real-world scenarios.

Table 4 Test results of computer vision models on 20 experimental diffractograms.
Full size table

Usage Notes

We strongly suggest following the data loading tutorials available at https://github.com/BCV-Uniandes/SIMPOD.git. We also recommend downloading only the JSON files if images are not needed.