US-CoastEX: Observation-based probabilistic reanalysis of storm surge and sea level extremes for the United States

Abstract

Reliable estimates of storm surge and sea level extremes with proper uncertainty quantification are key for cost-effective risk/adaptation planning. However, observational estimates are often unavailable or uncertain along most coastlines owing to data scarcity. Here, we provide a fully observational-driven probabilistic dataset (US-CoastEX) of storm surge and sea level extremes for the U.S. coast (1950–2020). Non-stationary extreme storm surge distributions are generated for gauged and ungauged sites by applying Bayesian methods to the U.S. tide gauge network, complemented with additional storm data unavailable in commonly used tide gauge data. The distributions are combined with tidal peak data to estimate return periods and levels of extreme sea levels and their uncertainty. Ou results show that traditional site-by-site estimates based on existing model data, as well as regionally-aggregated analysis of standard tide gauge data, have underestimated 100-year extreme sea levels by 50% (on average) along much of the U.S. coast, especially in regions exposed to extreme storms. The data supports coastal managers to make decisions, especially in vulnerable areas where in-situ sea-level monitoring is limited.

Background & Summary

Extreme sea level (ESL) events caused by storm surge extremes pose a threat to many coastal populations and natural ecosystems¹ especially when combined with high astronomical tides^1,2. The most extreme storm surge events develop during major storms, such as hurricanes and/or powerful extratropical storms, when extreme winds and low atmospheric pressure push ocean water ashore^1,2. Establishing robust estimates of storm surge and extreme sea level events with proper uncertainty quantification through statistical analysis of observational data is critical for coastal design and risk and adaptation assessments³. However, high-quality historical sea-level observations are only available at sites with tide gauges, leaving long coastal stretches without observational coverage^3,4,5. Furthermore, most tide gauges contain only a few years, or decades, of data, thereby providing only a limited sample of extremes. They also usually comprise gaps and/or erroneous or incomplete readings during major storms such as hurricane events^4,5,6. These limitations limit reliable estimates of the likelihoods of extreme events (and their changes over time) using site-by-site statistical analysis of observational data^4,5,6.

Global and regional storm surge hindcasts, and extended data-reconstructions from machine-learning methods, based on atmospheric reanalysis forcing fields provide spatially-continuous extreme data from which extreme value statistics can be obtained. However, such products tend to underestimate coastal storm surge extremes, partly due to their coarse resolution atmospheric reanalysis forcing that cannot properly resolve extreme values^6,7,8,9 and generally exhibit spurious climate variability and trends due to interplays between model biases and changes in historical observational data in reanalysis products^9,10,11,12. In addition, as with most tide gauge data, existing storm surge hindcasts generally cover a few decades, typically after 1980 when satellite records began to become available to constrain atmospheric reanalyses¹². Spatial statistical approaches such as regional frequency analysis (RFA)^13,14,15 offer an alternative to partially overcome several sampling limitations of traditional site-by-site analysis of storm extremes by fitting a particular extreme value distribution to sets of aggregated storm data pooled together (from tide gauges sites or model outputs) across coastal regions that are assumed to be coherent. However, while easy to apply, RFA approaches rely on subjective criteria to establish coastal sites with coherent extreme storm characteristics^13,14,15 and suffer from unsubstantiated statistical assumptions (e.g., neglecting spatial inter-site dependences and relying on unrealistic regional limits that generate discontinuous extreme storm surge fields)^13,14,15, which often result in unreliable estimates and/or misrepresented uncertainties.

Recently, more advanced spatial models for storm extremes have been used to overcome such limitations by resolving spatial dependencies in extremes, and in turn, enabling sharing of data information across tide gauge sites, and enabling predictions of surge extremes for ungauged sites^4,5,16,17. However, existing spatial models (and associated data sets) for the U.S. have relied on a limited number of long-term tide gauge data^16,17, thereby suffering from similar problems as site-by-site analyses, and are limited to contiguous U.S. regions which creates a limited basis situation for future coastal planning⁵. These models have also assumed that surge extremes are stationary^16,17 whilst surge extremes have been shown to have regional coherent and significant trends along widespread U.S. coastal regions¹⁸. These current limitations preclude robust flood risk assessment and cost-effective adaptation planning with potentially severe implications due to premature failure of flood defenses designed with erroneous predictions¹⁹. Consequently, there is an urgent need for more reliable and robust estimates of the occurrence probabilities of storm surge and sea level extremes with a rigorous treatment of uncertainty. This should also account for major storm extremes that happened in the past, but are not captured and resolved in commonly used coastal water level databases.

Here, we present a new observation-based probabilistic dataset (“US-CoastEX”) of storm surge and sea level extremes along the entire U.S coastline by applying an established non-stationary spatiotemporal Bayesian Hierarchical Framework (BAYEX)⁴ to the U.S. tide gauge network¹⁸ between 1950–2020. The complete dataset comprises two different versions: a standard version in which BAYEX is informed solely with high-quality tide gauge record data¹⁸ and an extended version where additional records from other sources (including sub-hourly tide gauge records, inferred extremes, last recorded water levels or high-water marks) are processed and also used to support BAYEX in addition to the standard hourly tide gauge records. BAYEX resolves tide gauge dependences in space and time and models extreme storm surge fields as a nonstationary continuous process consistent with underlying climatological storm patterns. The consideration for such dependences in BAYEX compensates for data spareness (i.e., allows accommodation of data gaps), reduces uncertainty for coastal gauged sites and enables estimates of storm surge distribution data for ungauged sites^4,18.

In addition to providing storm surge data, our dataset also contains ESL return period estimates estimated by combining BAYEX-inferred skew surge distribution data with astronomical tidal distributions. These estimates are compared to published ESL estimates used to inform coastal hazard and/or risk flood assessments, highlighting that return levels and return periods of ESL events have been underpredicted on widespread U.S. coastal regions relative to other products.

The data provided can support coastal managers to make more confident decisions, especially along many U.S. coastlines that are vulnerable and where long-term in-situ sea level monitoring is limited or non-existent. Our fully-empirical dataset provides supports for a range of coastal engineering and science needs (e.g., engineering design/management and coastal flood hazard and risk analysis). It provides, for instance, a new benchmark for validation of storm extremes and flood hazard estimates generated through numerical modeling (based on reanalysis climate data, synthetic storms or climate model projections) and extended data-reconstructions. It could also be directly combined with other relevant meteorological, hydrological and/or oceanographic extremes (e.g., rainfall and wind-waves) to estimate total water levels and other compound extremes. Thus, it fills an important gap, particularly for U.S. coastal regions such as Hawaii, Alaska, Puerto Rico/U.S Virgin Islands where historical in-situ sea level monitoring is limited or even non-existent (and which have been usually excluded from coastal climate assessments¹⁸). A summary of the data in US-CoastEX is fully described in Supplementary Information.

Methods

Bayesian Hierarchical Modeling with BAYEX

The BAYEX framework⁴ performs spatiotemporal Bayesian hierarchical modeling of coastal storm surge extremes and is represented as a product of conditional distributions or sub-models, or layers. These comprise: (1) an “observation model” that links the prescribed extreme data to the spatio-temporal processes; (2) a “process model” that accounts for underlying dynamics of the processes involved; and (3) a “parameter model” that considers the underlying uncertainties in the parameters and integrates any prior knowledge about the prescribed data and underlying processes. The hierarchical model structure enables the assessment of the joint distribution of the processes and parameters conditioned on the data (also known as the posterior distribution), while rigorously propagating the uncertainties underlying the data, processes, and parameters⁴. These types of Bayesian Hierarchical Models (BMH) have been applied across various science disciplines (e.g., hydrology²⁰ and ecology²¹) to enable robust statistical estimates, especially in contexts characterized by data scarcity and high uncertainty.

In modeling spatial inter-site dependences of storm surge extremes, BAYEX resolves residual dependence (sites with co-occurrence of storm extremes) and climatological dependence (sites with similar and/or consistent storminess but not necessarily co-occurrence of storm extremes). Residual dependence is resolved using a max-stable process^4,16,22 (i.e., an infinite-dimensional generalization of a Generalized Extreme Value (GEV) distribution) and storm climatological dependence is here captured using latent Gaussian processes with random effects and physical bathymetric covariates (continental shelf width estimated using Natural Earth 200-meter depth contour line)⁴. In other words, residual dependence implies dependence among annual maxima whereas climatological dependence reflects spatial association amongst the GEV parameters⁴. The marginal distribution at any particular site follows a univariate GEV distribution based on max-stable process theory, with parameters μ (location), σ (scale), and ξ (shape). The location parameter, μ, is modelled as a spatial time-evolving process (using an integrated random walk) to account for climatological storm frequency changes. The GEV scale and shape parameters follow a spatial-varying, stationary process. An extensive description of BAYEX including its formulation, implementation and testing, has already been provided elsewhere^4,14, and thus we only provide a brief description of its observation and process model layers. The likelihood can be written as^4,22:

$${Y}_{t}\left({s}_{i}\right)|{\theta }_{t}\left({s}_{i}\right),{\mu }_{t}\left({s}_{i}\right),\sigma \left({s}_{i}\right),\xi ({s}_{i}),\alpha \sim {GEV}\left({\mu }_{t}^{* }\left({s}_{i}\right),{\sigma }_{t}^{* }\left({s}_{i}\right),\alpha {\xi }^{* }({s}_{i})\right),$$

(1)

$${\mu }_{t}^{* }\left(s\right)={\mu }_{t}\left(s\right)+\frac{\sigma (s)}{\xi }\left({{\theta }_{t}\left(s\right)}^{\xi (s)}-1\right),$$

(2)

$${\sigma }_{t}^{* }\left({s}_{i}\right)=\alpha \sigma \left(s\right){{\theta }_{t}\left(s\right)}^{\xi \left(s\right)},$$

(3)

where ${Y}_{t}\left({s}_{i}\right)$ is the annual maximum surge (m) for year $t$ at site ${s}_{i}$, and ${\theta }_{t}\left(s\right)$ is a spatial process resolving residual dependence and $\alpha$ ∈ (0,1) is a parameter that controls the relative contribution of small-scale errors. The GEV shape parameter, ξ, is allowed to vary in space, according to a Gaussian process¹⁸:

$$\xi (s) \sim GP(\underline{\xi },c(s,s{\prime} ;{\gamma }_{\xi },{\rho }_{\xi })),$$

(4)

where $GP(\underline{\xi },c(s,s{\prime} ;{\gamma }_{\xi },{\rho }_{\xi }))$ is a Gaussian process with mean $\underline{\xi }$ and covariance function c(,∙). The hyperparameters ${\gamma }_{\xi }$ and ${\rho }_{\xi }$ denote, respectively, standard deviation and length scale values defining the covariance function⁴.

The GEV location parameter ${\mu }_{t}\left(s\right)$ is assumed to vary smoothly through time (to resolve long-term changes such as nonlinear trends as opposed to shorter-term variations, which are likely unresolvable) using a spatio-temporal integrated random walk according to⁴:

$${\mu }_{t}\left(s\right)={\mu }_{t-1}\left(s\right)+{\mu }_{{trend},t-1}\left(s\right),$$

(5)

$${\mu }_{{trend},t}\left(s\right)={\mu }_{{trend},t-1}\left(s\right)+{\omega }_{t}\left(s\right),$$

(6)

where ${\omega }_{t}\left(s\right)$ is a zero-mean Gaussian process ${\omega }_{t}\left(s\right) \sim {GP}\left(0,c\left(s,s{\prime} ;{\gamma }_{\mu },{\rho }_{\mu }\right)\right)$.

The extended description of all BAYEX process layers and parameters, including all Gaussian processes and initial states of $\mu$, see refs. ^4,5. The full description of the BAYEX spatial domain and the statistical inference process and model diagnostics analysis has been provided in ref. ¹⁸. In total, 6,000 distribution samples (post-warm-up draws for analysis) are provided by BAYEX (after a warm-up phase) for gauged and ungauged sites along the U.S. coastline (Fig. S1)¹⁸.

Observational data for BAYEX

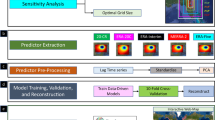
US-CoastEX includes extreme skew surge distributions (Fig. S3 shows posterior-median and 90% credible intervals) in addition to ESL estimates derived through BAYEX based on annual maximum skew surge data obtained from different data sources (Tables S1-S2) as shown below and illustrated in Fig. 1.

Fig. 1

Methodological framework diagram. The orange-shaded section displays the general workflow used to generate BAYESL-TG/EXT while the blue-shaded section shows the general workflow used to estimate the extreme sea level data from BAYESL-TG/EXT. The application of BAYES-TG uses only annual maxima skew surge data from observed hourly tide gauge sea-level records (as shown by the dashed violet line and the asterisk ‘*’).

Standard version (BAYESL-TG)

In the standard application of BAYEX (henceforth BAYESL-TG), the model is informed solely by historical time series of annual maxima skew surge (used synonymously with storm surge) derived from high quality hourly sea-level records (1950–2020) from 208 open-coast tide gauge sites included in the GESLA-2 (Global Extreme Sea Level Analysis) database (retrieved from: https://www.bodc.ac.uk/resources/inventories/edmed/report/6562/)²³ (Figs. S1, S2). Skew surge (defined as the absolute difference between observed high-water level and the closest predicted high tide regardless of their timing over a tidal cycle) has been shown to be a reliable metric of storm surge under different tidal regimes²⁴. Note that tide gauge data included in GESLA-2 are very similar to records in GESLA-3, as most updates and new data are for estuarine, river and lake regions, which are not used here, as further discussed below. We require 70% of all hourly records over a given year to determine an annual maximum. We remove any underlying mean sea level changes and its underlying variability by removing a centered 30-day moving average from the observed water level data. The data is also visually scrutinized and the corrected when required for any datum shifts and tsunamis. The tidal signal was extracted using a year-by-year harmonic analysis. This analysis is entirely focused on open-coastal regions where storm surge extremes are mainly driven by wind and pressure effects. Therefore, only tide gauges within a maximum of 5 km from a coastline are used and locations further within deltas, narrow inlets, bays and tidal rivers, have been removed to minimize major effects of hyper-local geography, river discharge and/or nonlinear interactions which generally lead to very different storm surge extremes than events experienced along open-coastal regions. The full description of the data processing is available elsewhere¹⁸. The exact location of the tide gauge sites, and their record length, are shown in Fig. S1. The samples of GEV model parameters (summarized as posterior-medians and 90% CI within Fig. S3) and annual maxima from BAYESL-TG/EXT are archived without further processing (Table S3). A full discussion of BAYESL-TG extreme skew surge data is also provided in ref. ¹⁸.

Extended version (BAYS-TG/EXT)

Hourly tide gauge records provide high-quality ESL information but since they generally have hourly resolution, they could miss absolute peaks of storm events when there are larger changes in water levels at sub-hourly levels, as occurs more often during major events. In addition, it is well documented that during major storms (e.g., Camille and Katrina) there is typically missing data due to tide gauge damage or malfunction^25,26. Hence, we provide an extended-data version (BAYESL-TG/Extended) where BAYEX has been informed not only by historical time series of annual maxima skew surge from hourly sea-level records, but also with extreme surges from NOAA top-ten water level data archives (https://api.tidesandcurrents.noaa.gov/dpapi/prod/)²⁷, including 6-min tide gauge records (after 1996), inferred extremes (derived through gap-filling procedures due to missing data), last recorded extreme water levels (last successfully recorded level before tide gauge malfunction during a storm) and high water marks and storm-tide peaks from SURGEDAT’s database (https://surge.climate.lsu.edu/data.html#GlobalMap) (Tables S1-S2)²⁶. In Fig. 1 (and Table S1 and Fig. S4) we present a brief comparison of BAYESL-TG and BAYESL-TG/EXT. The top-ten water-level information data from NOAA contains tide gauge codes, station names, peak dates & times, height, datum (MSL) and source²⁷. The SURGEDAT data²⁶ provides location, year and datum (for specific events) and recorded (or observed) water level data. Storm surge events before 1950 and after 2020 have been removed for consistency. Storm events retrieved from SURGEDAT²⁶ are only considered when reported as ‘storm tides’ (without breaking wind-wave influence) and with datum (described as height relative to normal tides, i.e., MSL) and their documented locations are within 20 miles from a tide gauge. The peak date and time are retrieved from NOAA’s extreme water level meteorological reports and confirmed using historical hurricane track data²⁸. Any extreme events prior to 2020 have been updated (or corrected) to present-day MSL (2020) by adding MSL rise between the year of the recorded events and 2020) using relative MSL trends estimated by NOAA. There are a few tide gauge locations where no relative MSL trends are available and thus the values from the nearest tide gauge locations are used. The skew surge associated with each extreme water level event is determined by removing the closest tidal peak values extracted from NOAA’s tide prediction records, using their respective peak date and time, with all events brought to the same reference datum (MSL). For events where peak times are not provided (or available), tidal peak averages from that particular day have been used. In total, 1084 skew surge events have been estimated. We then compare these values with annual maxima skew surges previously estimated for those years using hourly tide gauge data, i.e., used to inform BAYESL-TG as previously described. The highest values within each year are therefore used as annual maxima. In total, 775 annual maxima skew surge values estimated from hourly tide gauge data are replaced by new, updated annual maxima skew surges, 652 obtained from processed NOAA top-ten water-level data, 2 from NOAA NWS data archives, and 7 from the SURGEDAT (Table S2). BAYESL-TG/EXT (extended version) and BAYESL-TG (standard version) use the same values for Alaska, Puerto Rico and the U.S. Virgin Islands, since no relevant annual maxima events have been identified across other complementary data sources (i.e., compared against annual maxima obtained from standard hourly tide gauge records). The GEV parameters associated with BAYESL-TG and BAYESL-TG/EXT are archived without further processing (see Table S3).

Estimation of ESL return levels using BAYEX outputs

ESL occurrences depend upon tidal processes and storm surges²⁹. Here we use two approaches that are typically used to calculate ESL return levels from skew surge and tidal data²⁹. The first approach (henceforth “Method 1”) convolves the probability distributions of deterministic tidal peak data and stochastic storm surge data. This convolution approach allows us to use complete tidal information, which is not possible through direct analysis of still water levels (Fig. S5)²⁹. The probability of a given ESL event is thereafter derived from the joint cumulative distribution function. The convolution integral is given by²⁹:

$$F\left(z\right)=\int {G}_{r}\left(z-x\right)f\left(x\right){dx}$$

(7)

where ${G}_{r}$ is the (GEV) distribution of extreme skew surges and $f$ is the density function of the tidal peaks over a full 18.61-year nodal tidal cycle. This approach assumes skew surge and tide independence with an equal probability of a given skew surge occurring at any high tide²⁸. We convolve 6,000 skew surge distribution samples from BAYEX with tidal peak data, generating a total of 6,000 ESL return period curves from which posterior-median values and associated 90% credible intervals are calculated. The second approach (henceforth Method 2) adds a fixed tide level (such as Mean High Water (MHW), Mean Higher High Water (MHHW), or Highest Astronomical Tide (HAT)) (Fig. S6) to estimates of extreme surge levels^9,23. Although we use Method 1 as reference in this analysis, we also provide alternative ESL estimates derived using fixed tide levels MHW, MHHW, and HAT (Fig. S6), aligning with previous research^15,29; but other tidal levels could be used. The observed tidal peaks at gauged locations are obtained from GESLA water level time series via harmonic analysis (using the same time series from which annual maxima skew surge levels are obtained to inform BAYEX). Fig. S5 shows a comparison of 100-year ESL events derived using the different alternative methods at tide gauge sites using GESLA-based tidal peak data. The comparison shows that Method 1 (convolution) and Method 2 (when adding MHHW to estimates of storm surge return levels) result in consistent 100-year ESL return levels almost everywhere (differences of less than 0.20 cm); except along macro-tidal coastal regions where tidal influences dominate over maximum surge levels (e.g., Gulf of Alaska and/or Bay of Fundy). The 100-year ESL return levels obtained using HAT (Method 2) illustrate a very conservative (assume that extreme surge events always happen during HAT²⁹) and exceed estimates from Method 1, everywhere, particularly on coastlines with considerable tidal ranges as mentioned before.

At ungauged sites, high tide values are derived by applying harmonic analysis to the barotropic tidal TPXO9-atlas model (version 5) dataset, a product that exhibits a very small deviation (<10 cm) in terms of harmonic constituents relative to tide gauge data (https://www.tpxo.net/home)^30,31. The distribution of high tides from TPXO9v4 spans a full 18.6-year nodal tidal cycle. The comparison of MHHW and HAT tide levels from TXPO9v5 and GESLA for tide gauge stations (Fig. S6) shows that TPXO9v5 and GESLA-based MHHW and HAT agree well at most coastal sites with absolute differences of less than 0.1 m and 0.3 m, respectively. Note that tidal peak records from other tidal model products could be used to determine ESL estimates at ungauged sites based on BAYEX skew surge data. Figure 2 presents 100-year ESL return levels (relative to mean sea level) calculated from BAYESL-TG/EXT through Method 1 and Fig. 3 presents their associated 90% credible intervals (CI). In Fig. 4, absolute and relative differences between 100-year ESL estimates derived using BAYESL-TG and BAYESL-TG/EXT data are provided. The differences shown in Fig. 4 result from incorporating important extreme storm surge events not included in standard commonly-used hourly tide gauge records, as previously described (Table S1 and Fig. S4). Tide gauge sites are often 10 s to 100 s km apart from each and prone to missing and/or underestimating peaks due to storms making landfall between gauged sites. In addition, as previously discussed, hourly tide gauge data can miss absolute peaks of storm events at sub-hourly scales and/or generally comprise gaps and erroneous and/or incomplete readings during major storms including hurricanes (e.g., Katrina and Camille)^4,5,6 owing to tide gauge damage²⁵. Consequently, extreme outlier events could not be always captured in curated, global tide gauge datasets (e.g., NOAA, GESLA and UHAWAII archives). These results evidence that including additional observational sources of data is vital to enhancing estimates of storm surge and sea level extremes and that assessments relying entirely on hourly tide gauge observational data^32,33 could result in unpredicted higher return periods particularly in coastal regions exposed to TC events. This includes physical models that (generally) bias-adjust storm surge outputs and are validated based on tide gauge data^34,35. It is key to mention that even with pooling extreme data across areas through BAYEX and inclusion of additional extreme storm data (e.g., NOAA and SURGEDAT) beyond tide gauge records, estimates for TC areas remain highly uncertain (Fig. 3).

Fig. 2

100-year return levels (m) along the coastline of the U.S., Puerto Rico and the U.S. Virgin Islands. The estimates are calculated by convolving BAYESL-TG/EXT extreme skew surge data and TPXO tidal peak distributions. All estimates are all relative to present-day mean sea level (MSL).

Fig. 3

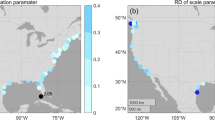
90% Credible interval (CI) width (m) associated with 100-year ESL return levels along the coastline of the U.S., Puerto Rico and the U.S. Virgin Islands. The estimates are calculated by convolving BAYESL-TG/EXT extreme skew surge data and TPXO9v5 tidal peak distributions. The latitude and longitude scales are as in Fig. 2.

Fig. 4

Absolute difference (m) between 100-year ESL return level estimates derived from BAYESL-TG and BAYESL-TG/EXT along the coastline of the U.S including Hawaii. The estimates are calculated by convolving BAYESL-TG and BAYESL-TG/EXT skew surge data with TPXO9v5 tidal peak distributions. The latitude and longitude scales are as in Fig. 2.

Data Records

The entire dataset (US-CoastEX) is archived at Zenodo³⁶ and provided in NetCDF format. The dataset contains 4 files with a total size of approximately 15 GB:

• 1) The files BAYESL-TG_GEV_PRED & BAYESL-TG-EXT_GEV_PRED comprise samples of non-stationary extreme skew surge distributions (GEV time-varying location, scale and shape), from BAYESL-TG and BAYESL-TG/EXT, respectively, for ungauged coastal U.S. sites (see Table S3 for further details);

• 2) The files BAYESL-TG_RL_ESL_PRED & BAYESL-TG-EXT_RL_ESL_PRED encompasses return level estimates of extreme sea levels for return periods of up to 1000 years, derived under different approaches (see Methods) based on BAYESL-TG and BAYESL-TG/EXT skew surge data and TPXO9v5 tidal peaks, respectively, for ungauged coastal U.S. sites (see Table S4 for further details);

The code that implements BAYEX is archived at Zenodo³⁷.

Data considerations

It must be mentioned, as previously discussed, that BAYESL-TG and BAYESL-TG/EXT have been developed for open-coast regions using only tide gauge data within less than 5 km from a coast. The application of BAYEX to the U.S. coastline¹⁵ (and associated data sets) (BAYESL-TG and BAYESL-TG/EXT) are hence not representative (or been tested or validated) of storm surge and sea level extremes in deltas, narrow inlets, bays and/or tidal rivers where hyperlocal geography, extensive river discharge, tidal influences and/or other nonlinear interactions could play a role. It should be noted though that a few specific tide gauges (with long-term data) used to inform BAYEX located within less than 5 km of a coast could still be affected by hyperlocal geography (e.g., New York and Delaware). It is also important to mention that that storm surge and tides are just two contributors to total water levels that result in flooding. The data provided here are for storm surge extremes (and sea level extremes) but coastal design/risk assessments often require total coastal water levels. These may be derived by combining BAYEX data with other relevant meteorological and/or oceanographic water level contributors (e.g., rainfall and wave setup) (and their associated uncertainty) with total water level products.

Complementary data sources

BAYESL-TG/EXT is informed not only by historical time series of annual maxima skew surge from hourly sea level records but also with complementary annual maxima data processed from NOAA top-ten water level and SURGEDAT archives (Tables S1-S2). That includes 6-min tide gauge records (after 1996), inferred extremes (determined using gap-filling procedures due to missing data), last successfully recorded extreme water levels prior to tide gauge malfunction during a storm and high water marks²⁷ and historical storm-tide peaks from SURGEDAT peak surge database (Table S1-S2)²⁶. The inclusion of multiple major TC storms (e.g., that produced maximum surge levels > 4 m; Hazel, Katrina or Camille) and other relevant events that do not exist in tide gauge records along with other relevant storms that have not been fully represented (and hence underestimated) by standard hourly tide gauge data result in much higher estimates compared to our standard BAYESL-TG version data (see Fig. 4; Fig. S4). Although we derive annual maxima skew surges only for storms with reported locations and datums (as previously mentioned), there is a degree of uncertainty introduced for specific inferred extremes and high-water marks where processing techniques have been applied (e.g., gap-filling procedures from NOAA) or when the exact peak time of major hurricanes are not reported (e.g., SURGEDAT) and therefore daily tidal peak needs to be averaged to derive skew surge estimates. It could also be possible that the few high-water marks labeled in SURGEDAT as storm-tides (without wave breaking influence) might still contain a wave-related component. It should be noted, however, that these uncertainties are rather small relative to the uncertainties associated with storm surge levels resulting from major storms. This is the case of many coastal areas exposed to major TC events (e.g., U.S. Gulf coastline) where storm surge extremes exceed 4 m (e.g., Carla, Camile, Katrina and Rita; Fig. S4) and differences between tidal peaks are extremely small (Fig. S6).

Model spatial knot grid

The Bayesian hierarchical model rigorously propagates the underlying uncertainties associated with the prescribed extreme data, processes and parameters. However, some considerations on the uncertainties associated with how we model residual dependence need to be discussed. The spatial residual process is expressed as a linear combination of scaled Gaussian kernels defined on a grid of spatial knots⁴, converging to a max-stable process asymptotically as the number of knots grows infinitely large. Here a consistent 0.5-degree knot grid covering the U.S. coast has been used to resolve the spatial residual process¹⁸, corresponding to the length scale and spatial extend of traditional historical TC storms (~500 km). The residual process is built using all the knots at each tide gauge location. The length scale of the spatial residual dependence represents the spatial distance over which the residuals (differences between observed vs predicted values) remain correlated⁴, representing how far spatial influences persist before becoming negligible. Increasing BAYEX grid knot to 0.2 degrees or less could yield even more precise estimates for particular areas. However, such an increase comes with trade-offs as it is only computationally tractable by building the residual process using the nearest ten knots to each tide gauge station. Regional sensitivity analysis conducted for Florida indicates that increasing BAYEX grid knot from 0.5 to 0.2 degrees (while using ten knots at each tide gauge location) results in a reduction of the location (μ) and scale (σ) parameters by< 5% and the shape parameter (ξ) by ~15% when average across all tide gauge sites. While this increase in resolution could help resolve smaller length scales, the reduction in the number of spatial knots used decreases the ability of BAYEX to capture important regional dependence along many coastal regions. For example, in the U.S. South and East Coasts and Gulf Coast, major TC storms often track coastlines for hundreds of miles, affecting multiple tide gauges relatively far apart. Neglecting such regional dependences results in underestimated GEV parameters within such regions, particularly ξ¹⁸.

Technical Validation

The adequacy and performance of BAYEX (and its underlying max-stable process) have been comprehensively assessed using tide gauge records, modeled storm surge simulations and synthetic storm data^4,5. The max-stable assumption in BAYEX for representing storm surge extremes has also been confirmed through leave-one-out cross-validation based on tide gauge observations^4,5. A full comparison of BAYEX skew surge (GEV) distribution parameters (and associated return period estimates) against estimates from conventional at-site GEV model based on Bayesian inference have been conducted for 208 tide gauges along the U.S. coastal areas¹⁸. Below, we compare our convoluted ESL return levels using BAYEX and TPXO9v5 data against published or reported estimates from different data set available.

Comparison of ESL estimates against NOAA observational estimates

Here we compare ESL return levels estimated based on BAYESL-TG/EXT data with published estimates using different data sets and statistical approaches. First, we compare 100-year ESL return level predictions from convolving BAYESL-TG/EXT extreme skew surge distributions and GESLA-based tidal peaks with values estimated by NOAA via regional frequency analysis (RFA)¹⁴ (https://sealevel.globalchange.gov/resources/2022-sea-level-rise-technical-report/) of tide gauge records (Figs. 4, 5). The comparison shows that 100-year ESL estimates presented here exceed estimates from NOAA for most tide gauge sites along the U.S. East and Gulf coasts by up to 1.5 m, depending on locations. The differences found at tide gauge sites along the U.S. West coast, Hawaii and Alaska are relatively small (i.e., typically less than 0.25 m) as extreme sea levels are generally dominated by high tides. A comparison of other return periods (25, 50, 75; and 100 years) is also presented highlighting that differences between estimates are already considerable beyond 25-year return periods for the U.S. East and Gulf coastline regions (Fig. 6). We note that there are multiple factors that can contribute to those differences, e.g., number and/or location of tide gauge sites, from which data was extracted, and their record lengths (as well as other data sources used to complement such records), differences in the data processing steps, spatial model used and estimation methodology for calculation of ESL return periods (as shown in Table S1). It is impossible for us to isolate the differences due to the use of different statistical models, unless the exact same data sources, time period and data processing methods are used.

Fig. 5

Difference (m) between 100-year ESL return level estimates derived by convolving BAYESL-TG/EXT extreme skew surge distributions and GESLA tidal peak data against estimates reported by NOAA using RFA across different tide gauge sites. Only common tide gauge sites are shown. The latitude and longitude scales are as in Fig. 2.

Fig. 6

Comparison of 25, 50, 75 and 100-year ESL return level estimates (m) against those reported by NOAA for each region. Estimates are all relative to present-day mean sea level (MSL).

Comparison of ESL estimates against numerical model-based estimates

We also compare BAYESL-TG/EXT return periods obtained through Method 1 with estimates calculated from a widely-used storm-tide model hindcast dataset (CODEC)³⁴ covering 38-years between 1979–2017 (Table S1). This enables a comparison along the entire coastlines and not just for tide gauge sites. The extreme surge distribution estimated from CODEC data is derived by fitting a traditional GEV to annual maxima skew surge (m) time series for each model point separately (through maximum likelihood estimation), from which ESL return periods are then calculated through convolution based on tidal peaks from TPXO9, for direct comparison. Figure 7 compares 100-year ESL estimates through Method 1 and CODEC for all U.S. coastal regions. These results show that 100-year ESL return levels estimated from BAYESL-TG/EXT exceed site-by-site CODEC estimates for approximately 87% of the U.S. coastline by 65% on average. Similar results are found when fitting a Generalized Pareto Distribution (GPD) to CODEC data (not shown for simplicity). The exception is from Georgia to South Carolina, where single-site CODEC 100-year ESL estimates exceed BAYESL-TG-EXT based on Method 1 by up to 0.5 m (Fig. 7). In Fig. S7, we present return periods (years) using BAYESL-TG-EXT data for ESL that are estimated to have a 100-year return period based on at-site100-year ESL return levels based on CODEC data, indicating that (on average) extreme events of that magnitude are nearly three times more likely to actually occur (i.e., a 35-year return period event) as estimated from BAYESL-TG/EXT data. In many major coastal cities, such ESL events are up to 20 times more likely according to our results (e.g., New York, Tampa, Miami, San Francisco, Boston, Seattle and Honolulu; see Fig. S8). These considerable differences originate from the use of different data sources (observational archives versus simulated data; as shown in Fig. S9) and statistical methods (spatio-temporal BHM modeling versus traditional at-site analysis of surge extremes) as previously shown in ref. ¹⁸ (Table S1). In addition, we show a comparison against published 100-year ESL estimates retrieved from COAST-RP (https://data.4tu.nl/articles/_/13392314)³⁵ - which have been obtained empirically from numerical surge simulations forced with synthetic storm tracks from a TC-database (STORM)³⁸ and extra-tropical storms from ECMWF’s ERA5 reanalysis forcing³⁵ (Fig. S10). We detect nearly identical differences (ca. Figure 7 and Fig. S9) with 100-year return level estimates from BAYESL-TG/EXT exceeding COAST-RP estimates for 76% of the U.S. coastlines by 50% on average.

Fig. 7

Comparison of 100-year ESL return levels (m) derived by convolving BAYESL-TG/EXT and TPXO9 tidal peak data with estimates from at-site GEV analysis based on CODEC data along the coastline of the U.S., Puerto Rico and the U.S. Virgin Islands. To facilitate visualization, only every grid point is shown. The comparison against COAST-RP (which includes synthetic storms) is provided in Fig. S10. The latitude and longitude scales are as in Fig. 2.

Comparison of ESL estimates with FEMA total water levels

To further contextualize our estimates, we provide comparison of 100-year ESL return levels based on BAYESL-TG/EXT against 100-year total water level return level estimates (referred to as stillwater elevation by the Federal Emergency Management Agency (FEMA) and includes astronomical tide, storm surge, and wave setup contributions) developed by FEMA³⁹ to support floodplain management and flood insurance purchase requirements within the U.S. (Fig. S11). Despite not including wave setup, which can be a key contributor to coastal extreme stillwater elevations, we find that 100-year ESL return levels based on BAYESL-TG/EXT usually exceed or are on par with FEMA estimates for tide gauge locations along the U.S. Gulf and East Coasts. Our comparison is less useful for the U.S. West Coast, where wave setup is a major contribution to sea level extremes (relative to storm surge events). There, not surprisingly, FEMA 100-year total water levels (and referred by FEMA as stillwater elevation) exceed BAYESL-TG/EX ESL estimates. FEMA estimates hold considerable authority in the U.S. However, to our knowledge, very few comparisons have been made against other methodological approaches, including in terms of uncertainty propagation and/or quantification. We hypothesize that this may be due to the absence of a single, centralized dataset – data are dispersed across hundreds of FEMA Flood Insurance Studies - and the existing lack of a standardized approaches and/or metrics for storm surge and wave.