Background & Summary

Gross primary production (GPP) is a key measure of how ecosystems capture and convert solar energy into organic carbon through photosynthesis, which is crucial for carbon storage and the functioning of the Earth’s carbon cycle1,2,3,4. Numerous remote sensing-based GPP datasets are freely accessible, including those that employ machine learning techniques5,6, process-based models7,8, light use efficiency (LUE) models9,10,11, and solar-induced fluorescence12,13. However, these datasets typically operate at coarse spatial resolutions (e.g., 500 m or coarser) and temporal intervals (e.g., 8 days or longer). The enhancement of both spatial and temporal resolutions in GPP datasets is vital for gaining deeper insights into ecosystem processes and improving carbon cycle models.

Recent advancements have seen significant progress in generating high-resolution GPP datasets at a nationwide scale. Robinson et al.14 successfully applied the big-leaf Moderate-resolution Imaging Spectroradiometer (MODIS) algorithm to produce a GPP dataset at 30-m resolution covering the United States, marking the first such product at fine resolution in this region. More recently, Lin et al.15 developed a 30-m resolution version of Global LAnd Surface Satellite (GLASS) GPP dataset by employing the two-leaf eddy covariance (EC) LUE model specifically for China. These datasets were developed at a national scale primarily due to limitations in global-scale applications, such as limitations in accessing high-resolution remote sensing data and the substantial computational resources required. While their work represents significant progress in enhancing spatial resolution, temporal resolution in GPP datasets remains relatively underexplored.

From a temporal perspective, the non-linear responses of plant photosynthesis to meteorological fluctuations are smoothed out in coarse-resolution GPP datasets. Over a 6-hour period, Wang et al.16 revealed that the total GPP summed from 1-hour estimates showed a much better match with EC GPP across 194 global sites, compared to those directly modeled at the 6-hour resolution. The reduced accuracy of course-resolution GPP arises from scaling uncertainty, a phenomenon widely reported in the modeling of ecological process parameters such as GPP17,18,19, net primary production20,21, and evapotranspiration22,23. Despite the scaling uncertainty, 1-hour GPP datasets can reflect the immediate responses of vegetation to environmental changes such as variations in light intensity24,25, temperature12,26, and humidity27,28,29. Therefore, improving the temporal resolution of GPP datasets to an hourly interval is essential for gaining a finer and more precise insight into terrestrial carbon dynamics.

LUE models offer significant advantages at the global scale, primarily due to their low parameter demands and the ease of integrating remote sensing data30,31. These models mainly rely on two input types: vegetation properties (such as vegetation type and leaf area index) and meteorological variables. Vegetation properties, which are typically derived from remote sensing data, remain relatively stable over longer periods from weeks to years32,33,34. In contrast, meteorological variables exhibit greater temporal variability and are typically sourced from reanalysis datasets. The development of 1-hour reanalysis datasets, such as the fifth generation of European ReAnalysis (ERA5)35, now enables the provision of GPP datasets at 1-hour intervals.

In this research, we developed a fine-resolution terrestrial GPP dataset for the period 2001–2020 at global-scale, based on a modified radiation scalar two-leaf LUE (RTL-LUE) model36,37,38. The RTL-LUE GPP dataset was generated at a 1-hour temporal resolution and a spatial resolution of 0.1°, using multiple inputs from land component of ERA5 (ERA5-land), GLASS leaf area index (LAI), MODIS land map, and NOAA atmospheric CO2 concentration. We validated the RTL-LUE GPP at the 184 EC flux sites, with 1-hour EC GPP serving as references. Additionally, we compared the RTL-LUE GPP with two coarser temporal resolution LUE-based GPP dataset, including the big-leaf MODIS GPP dataset (MOD17A2)39 and the two-leaf LUE (TL-LUE) dataset40,41. The high temporal resolution of the RTL-LUE GPP dataset can provide a more detailed perspective on terrestrial carbon dynamics and improving insights into the temporal dynamics of global carbon fluxes.

Methods

RTL-LUE model description

The model employed in the work is RTL-LUE model developed from the TL-LUE model, is effective in capturing temporal variations in GPP36,37,38. In this model, all leaves share the same maximum LUE, with differences in their LUE values determined by a radiation coefficient. The calculations of the RTL-LUE model are presented in the equations below:

$${GPP}={\varepsilon }_{max}\times (\,{f}({PPF}{{D}}_{{su}})\times {APA}{{R}}_{{su}}+{f}({PPF}{{D}}_{{sh}})\times {APA}{{R}}_{{sh}})\times {f}({VP}{{D}}_{{\rm{a}}{\rm{v}}{\rm{e}}})\times {g}({{T}}_{{\min }})\times {{C}}_{{s}}$$
(1)

where εmax represents the maximum light use efficiency across all leaves; APARsu and APARsh indicate the photosynthetically active radiation (PAR) absorbed by sunlit and shaded leaves, respectively, and are defined as follows:

$${APA}{{R}}_{{su}}=(1-{\alpha })\times \left[\frac{{PA}{{R}}_{{dir}}\times \,\cos ({\beta })}{\cos ({\theta })}+\frac{{PA}{{R}}_{{dif}}-{PA}{{R}}_{{dif}{,}{u}}}{{LAI}}\right]\times {LA}{{I}}_{{su}}$$
(2)
$${APA}{{R}}_{{sh}}=(1-{\alpha })\times \left[\frac{{PA}{{R}}_{{dif}}-{PA}{{R}}_{{dif}{,}{u}}}{{LAI}}+{C}\right]\times {LA}{{I}}_{{sh}}$$
(3)
$${LA}{{I}}_{{s}{\rm{u}}}=2\times \cos ({\theta })\times \left(1-{\rm{e}}{\rm{x}}{\rm{p}}\left(-0.5\times \Omega \times \frac{{LAI}}{\cos ({\theta })}\right)\right)$$
(4)
$${LA}{{I}}_{{s}{\rm{h}}}={LAI}-{LA}{{I}}_{{su}}$$
(5)

where α is the albedo; β is the mean angle between the leaves and incident solar radiation; θ refers to the solar zenith angle; PARdir, PARdif, and PARdif,u, represent direct and diffuse PAR above the canopy and diffuse PAR under the canopy, respectively, while C indicating the influence of multiple scattering for direct light; Ω indicates the level of leaf clumping in the canopy by describing their non-random spatial distribution; LAIsu and LAIsh refer to the LAI of sunlit and shaded leaves.

The radiation scalars f(PPFDsu) and f(PPFDsh), corresponding to sunlit and shaded leaves, are derived from the photosynthetic photon flux density (PPFD) through an identical functional form as shown below42:

$${f}({PPFD})=\frac{{b}}{{a}\times {PPFD}+{b}}$$
(6)

where a represents the coefficients that modulate the sensitivity of LUE to PPFD and are parameterized according to plant functional types (PFTs); b is a constant value set at 1 mol/m2/hh, which remains unchanged across all relevant calculations.

The scalar functions of the water stress (VPDave), temperature (Tmin), and the newly introduced CO2 concentration (Cs)40,43, each with a range from 0 to 1, are calculated as follows:

$${f}({VP}{{D}}_{{\rm{ave}}})=\{\begin{array}{cc}0 & {VP}{{D}}_{{\rm{ave}}}\ge {PVP}{{D}}_{{\rm{M}}{\rm{A}}{\rm{X}}}\\ \frac{{PVP}{{D}}_{{\rm{M}}{\rm{A}}{\rm{X}}}-{VP}{{D}}_{{\rm{ave}}}}{{PVP}{{D}}_{{\rm{M}}{\rm{A}}{\rm{X}}}-{PVP}{{D}}_{{\rm{M}}{\rm{I}}{\rm{N}}}} & {PVP}{{D}}_{{\rm{M}}{\rm{I}}{\rm{N}}} < {VP}{{D}}_{{\rm{ave}}} < {PVP}{{D}}_{{\rm{M}}{\rm{A}}{\rm{X}}}\\ 1 & {VP}{{D}}_{{\rm{ave}}}\le {PVP}{{D}}_{{\rm{M}}{\rm{I}}{\rm{N}}}\end{array}$$
(7)
$${g}({{T}}_{{\rm{m}}{\rm{i}}{\rm{n}}})=\{\begin{array}{cc}1 & {{T}}_{{\rm{m}}{\rm{i}}{\rm{n}}}\ge {P}{{T}}_{{\rm{M}}{\rm{A}}{\rm{X}}}\\ \frac{{{T}}_{{\rm{m}}{\rm{i}}{\rm{n}}}-{P}{{T}}_{{\rm{M}}{\rm{I}}{\rm{N}}}}{{P}{{T}}_{{\rm{M}}{\rm{A}}{\rm{X}}}-{P}{{T}}_{{\rm{M}}{\rm{I}}{\rm{N}}}} & {P}{{T}}_{{\rm{M}}{\rm{I}}{\rm{N}}} < {{T}}_{{\rm{m}}{\rm{i}}{\rm{n}}} < {P}{{T}}_{{\rm{M}}{\rm{A}}{\rm{X}}}\\ 0 & {{T}}_{{\rm{m}}{\rm{i}}{\rm{n}}}\le {P}{{T}}_{{\rm{M}}{\rm{I}}{\rm{N}}}\end{array}$$
(8)
$${{C}}_{{s}}=\frac{{{C}}_{{i}}-{{\Gamma }}^{\ast }}{{{C}}_{{i}}+2\times {{\Gamma }}^{\ast }}$$
(9)

where VPDave represents the hourly average vapor pressure deficit; Tmin refers to minimum temperature of the day; Ci and Γ* are the intercellular CO2 concentration and the CO2 compensation point calculated without considering dark respiration44, respectively; PVPDMAX, PVPDMIN, PTMAX, and PTMIN are model parameters specific to PFTs.

Data preparation

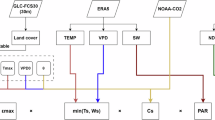
The RTL-LUE GPP product, generated using ERA5-land45, GLASS LAI32,46, MODIS land cover39, and NOAA CO2 concentration data, has a temporal resolution of 1 hour and a spatial resolution of 0.1°. We selected the downward shortwave radiation (DSR), dewpoint temperature (DPT), and air temperature (TA) from ERA5-land with a spatial resolution of 0.1° from 2001–2020. The vapor pressure deficit (VPD) was derived from TA and DPT according to Wang et al.16. Subsequently, VPDave was calculated based on VPD, while Tmin was obtained from TA. The GLASS LAI dataset with temporal resolution of 8-day and spatial resolution of 0.05°, was procured from the University of Maryland for the period spanning 2001 to 2020. A modified version of the Whittaker trend filter was employed to remove remaining noise from the LAI temporal data47. The annual International Geosphere-Biosphere Programme (IGBP) land cover maps in MCD12C1 were also used, providing a spatial resolution of 0.05° from 2001 to 2020. Finally, these original LAI and land cover maps were aggregated to a 0.1°resolution to ensure consistency with the climate datasets used in this study. Monthly CO2 concentration data from the NOAA Earth System Research Laboratory (ESRL) were used to construct the scalar function for CO2 concentration.

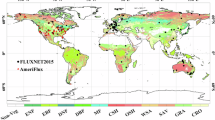
Via the FLUXNET2015 network, we selected 184 sites based on available observations for more than one year during 2001–2014 (Table S1)48. These sites include deciduous broadleaf forest (DBF, 22 sites), deciduous needleleaf forest (DNF, 1 site), evergreen broadleaf forest (EBF, 14 sites), evergreen needleleaf forest (ENF, 42 sites), mixed forest (MF, 9 sites), grass (GRA, 34 sites), crop (CRO, 18 sites), closed shrub (CSH, 2 sites), open shrub (OSH, 12 sites), wetlands (WET, 16 sites), savannas (SAV, 8 sites), woody savannas (WSA, 6 sites). In this study, the EC GPP (GPP_DT_VUT_REF) was initially provided at half-hour resolution and then aggregated into 1-hour intervals for model calibration and validation. Additionally, we also obtained two coarser temporal resolution LUE-based GPP datasets, including the big-leaf MOD17A2 dataset39 and the TL-LUE dataset40,41. To enable direct comparisons, these two GPP datasets were spatially interpolated to match the spatial resolution of the RTL-LUE GPP. Table 1 provided comprehensive details about the products used in this study.

Table 1 Summary of products adopted in the research.
Full size table

Generation and evaluation scheme for the proposed GPP dataset

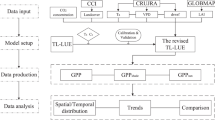
The process flowchart for the RTL-LUE GPP is displayed in Fig. 1. Firstly, two sensitive parameters including the maximum LUE (εmax) and the proportion of LUE relative to PPFD (a), were optimized for each PFT using the FLUXNET2015 dataset. For each site, one year of site data was randomly selected, and the parameter values corresponding to the maximum of agreement index (d) were identified as the optimization results49:

$${d}=1\,-\,\frac{\mathop{\sum }\limits_{{i}=1}^{{N}}{({Pi}-{Oi})}^{2}}{\mathop{\sum }\limits_{{i}=1}^{{N}}{(|{Pi}-\overline{{O}}|+|{Oi}-\overline{{O}}|)}^{2}}$$
(10)

where N represents the total count of 1-hour EC GPP; Oi is EC GPP value; \(\bar{{\rm{O}}}\) is the average of 1-hour EC GPP; Pi denotes the 1-hour RTL-LUE GPP, which is derived using ERA5-Land meteorological data as input. The optimized parameter values are documented in Table S2.

Fig. 1
figure 1

Workflow for generating and evaluating the proposed GPP dataset.

Full size image

Following the optimization of model parameters, 1-hour RTL-LUE GPP dataset was generated using meteorological data (including DSR, Tmin, and VPDave from ERA5-land), GLASS LAI maps, and MOD12C1 land cover maps. For model validation, the reliability of RTL-LUE GPP was assessed by comparing it with EC GPP at the 1-hour scale. At the global scale, RTL-LUE GPP was compared with TL-LUE and MOD17A2 GPP to evaluate inter-product differences in spatial patterns and annual total values.

Data Records

This dataset provides global gridded GPP with a temporal resolution of 1-hour and a spatial resolution of 0.1° for the period 2001–2020. The dataset is organized by year into 20 compressed files in 7z format, totaling either 8760 or 8784 records per file depending on the year. Each archive contains GeoTiff files with geographic information and temporal metadata, with each record corresponding to 1-hour of GPP data. The filename convention follows the pattern: “RTL-LUE-GPP-V01-YYYYMMDDHH.tif”, in which “YYYY” stand for year, “MM” is the month, “DD” refers to the day, and “HH” is the hour (e.g., RTL-LUE-GPP-V01-2002010313.tif). All data are stored as 16-bit integers, with GPP values in units of gC/m2/h derived by multiplying the stored integers by a scaling factor of 0.0001. The dataset is publicly available at the Science Data Bank (https://doi.org/10.57760/sciencedb.2950050).

Data Overview

Multi-year averages of 1-hourly GPP maps at fixed UTC times reveal the diurnal characteristics of global vegetation photosynthesis (Fig. 2). The high-GPP region shifts longitudinally from east to west, in step with the progression of solar illumination driven by Earth’s rotation (Fig. 3). For instance, significant photosynthetic activity is apparent across Asia at 06:00 UTC, while high-GPP region is centered over the Americas at 15:00 UTC. Peak global GPP values are consistently found in the most densely vegetated regions, particularly the tropical rainforests of the Amazon, the Southeast Asian, and the Central Africa, reaching their maximum during their respective daylight hours.

Fig. 2
figure 2

Multi-year averages of 1-hourly GPP maps at fixed UTC times. Panels (a–h) represent hourly GPP averaged from the proposed RTL-LUE GPP dataset during 2001–2020.

Full size image
Fig. 3
figure 3

Multi-year average of 1-hourly GPP across different UTC times and longitude ranges. These values are averaged from the proposed RTL-LUE GPP dataset during 2001–2020.

Full size image

As shown in Fig. 4a, approximately 64.15% of the global vegetated land surface has a GPP range of 0 to 1000 gC/m2/yr, 22.85% falls within 1000 to 2000 gC/m2/yr, and 13.00% exceeds 2000 gC/m2/yr. The higher GPP is found in tropical rainforests, particularly in the Amazon, the Southeast Asian, and the Central Africa. In contrast, lower GPP is characteristic of arid, semi-arid, and high northern latitude regions. As shown in Fig. 4b, the GPP trend map from 2001 to 2020 indicates a widespread greening pattern. Overall, approximately 49.64% of the global vegetated land surface has a GPP trend of 0 to 5 gC/m2/yr2, 17.47% falls within 5 to 10 gC/m2/yr2, and 14.23% exceeds 10 gC/m2/yr2. The significant greening trends are observed across the Sahel, India, eastern China, Europe, and boreal regions. However, notable GPP declines are also detected in certain areas, primarily due to factors including land use changes, climate variability, and extreme meteorological events51,52,53.

Fig. 4
figure 4

The spatial patterns of the annual average GPP (a) and its trend (b). These values are averaged from the proposed RTL-LUE GPP dataset during 2001–2020.

Full size image

Technical Validation

Hourly validation via EC flux towers

Hourly validation of the RTL-LUE GPP at 184 EC towers is shown in Fig. 5. At the PFT scale, the average RTL-LUE GPP exhibits a strong linear correlation with EC GPP (Fig. 5a), with a high coefficient of determination (R2) of 0.84 and a low root-mean-square-error (RMSE) of 0.03 gC/m2/h. A minor systematic underestimation of RTL-LUE GPP is observed for EBF and DBF. The site-scale RTL-LUE GPP is also found to be a close match to EC GPP (Fig. 5b), with an average R2 of 0.61 and a RMSE of 0.15 gC/m2/h. A higher site-scale average R2 is found in EBF (0.77), CSH (0.74), MF (0.72), DBF (0.68), and ENF (0.66), followed by WET (0.62), WSA (0.61), SAV (0.61), and GRA (0.50), and is lower in OSH (0.47), CRO (0.46), and DNF (0.44).

Fig. 5
figure 5

Assessment of the RTL-LUE GPP against EC GPP at both PFTs (a) and site scales (b,c).

Full size image

Comparisons with other LUE-based GPP datasets

As shown in Fig. 6a,d, annual RTL-LUE GPP exhibits a stronger pixel-to-pixel correlation with TL-LUE GPP (R2 = 0.83, RMSE = 405.93 gC/m2/yr) than with MOD17A2 GPP (R2 = 0.72, RMSE = 428.83 gC/m2/yr). The differences between RTL-LUE GPP and TL-LUE GPP display a distinct global distribution (Fig. 6b). The majority of the global vegetated land surface (73.42%) falls within the range of −400 to 400 gC/m2/yr. Larger differences occur less frequently, with 13.09% of the area exhibiting differences between −800 and −400 gC/m2/yr and 9.28% between 400 and 800 gC/m2/yr. Extreme differences are rare, with only 2.22% of the area below −800 gC/m2/yr and 1.99% above 800 gC/m2/yr. As for the differences between RTL-LUE and MOD17A2 GPP (Fig. 6e), approximately 81.00% of the global vegetated areas lies between −400 and 400 gC/m2/yr. Larger differences are observed less frequently, with 2.35% of the area exhibiting differences between −800 and −400 gC/m2/yr and 12.55% between 400 and 800 gC/m2/yr. Extreme differences (either below −800 or above 800 gC/m2/yr) are rare, accounting for only 4.10% of the area.

Fig. 6
figure 6

Spatial comparisons between annual mean RTL-LUE GPP and other global LUE-based GPP. Panel (a) shows a global pixel-to-pixel comparison between RTL-LUE and TL-LUE GPP, while Panels (b,c) illustrate their spatial differences. Panels (d–f) shows the comparisons between RTL-LUE and MOD17A2 GPP. These GPP are averaged from corresponding GPP maps from 2001 to 2020, with all comparisons performed at a spatial resolution of 0.1° × 0.1°.

Full size image

As shown in Fig. 6c,f, the latitudinal profiles further reveal that RTL-LUE GPP has higher values than TL-LUE and MOD17A2 GPP across the tropical, subtropical, and mid-latitude continental regions of the Northern Hemisphere. In contrast, RTL-LUE showed comparatively smaller estimates at high latitudes above 50°N. Overall, RTL-LUE has a lower global total GPP (124.77 PgC/yr) compared to TL-LUE (126.92 PgC/yr), but it is higher than the MOD17A2 GPP (113.90 PgC/yr) during the years spanning 2001 to 2020 (Fig. 7). Furthermore, all three GPP datasets exhibit increasing trends during this period, with TL-LUE showing the highest rate of 0.51 PgC/yr2, followed by RTL-LUE (0.48 PgC/yr2) and MOD17A2 (0.41 PgC/yr2).

Fig. 7
figure 7

Global total RTL-LUE, TL-LUE, and MOD17A2 GPP. Significant trend for 2001–2020 is depicted by ** (p < 0.01).

Full size image

The closer similarity between RTL-LUE and TL-LUE can be explained by the fact that both are two-leaf models36,41, while MOD17A2 is based on a big-leaf framework. Previous studies also suggested that MOD17A2 GPP tends to underestimate significantly in regions with high LAI and during the peak growing season, leading to notably lower GPP estimates, similar to the findings in this study38,54. In addition, the slightly lower GPP estimated by RTL-LUE relative to TL-LUE is mainly attributed to the temporal resolution of the modeling16. RTL-LUE operates at an hourly scale, which allows it to capture short-term extreme stresses more effectively25,55,56. Taking water stress as an example, GPP typically peaks at an intermediate VPD, whereas both excessively high and low VPD values reduce GPP. When models operate at a daily scale, they rely on mean VPD values over the day, which tends to smooth out stress extremes and leads to higher GPP estimates38,54. By contrast, the hourly resolution of RTL-LUE better reflects the impact of these stress events, resulting in slightly lower but more realistic GPP values. It is well known that atmospheric CO2 concentrations have been continuously increasing in recent decades, and the associated CO2 fertilization effect has significantly enhanced global GPP57,58. This is reflected in the interannual variability of GPP estimates: the two models that account for the CO2 effect (RTL-LUE and TL-LUE) exhibit higher interannual variability, whereas the model that does not consider CO2 (MOD17A2) shows lower variability.

Uncertainties

Compared to more mechanistic process-based models8,59, although the fertilization effect of CO2 concentration was taken into account60,61, LUE models did not consider additional environmental influences (water content and nutrient availability), which can result in larger biases in GPP estimation62. Recent research estimates global GPP to be around 150  Pg C/yr63, which exceeds the values provided in this dataset, likely due to limitations such as light saturation and scaling effects64,65. Furthermore, parameter uncertainty arising from scale mismatches66,67 and the sparse distribution of observation sites48 further exacerbated the bias in GPP estimates. The relatively coarse spatial resolution of input data, such as LAI and meteorological variables, made it difficult to accurately match the footprint of eddy covariance flux observations, thus adding to model parameters uncertainty68. For vegetation types with a limited number of observation sites (e.g., DNF), the calibrated model parameters often failed to fully represent the actual physiological state of the vegetation. Numerous previous studies had usually demonstrated that the εmax of C4 crops was generally higher than that of C3 crops15,69. However, due to the inability of the MODIS land cover map to distinguish between C3 and C4 crop types, it was not possible to separately estimate their GPP, which led to reduced accuracy in GPP simulations for these vegetation types (Fig. 5). Moreover, existing studies have indicated that high cloud cover is generally prevalent in tropical regions70,71, which significantly increases the uncertainty in LAI and other satellite-derived data. Variations in input datasets further contribute to substantial discrepancies in the estimated GPP72,73.