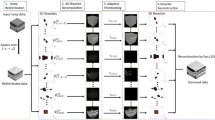
Abstract
Image quality datasets are used to train and evaluate predictive models of subjective human perception. However, most existing datasets focus on distortions commonly found in digital media and not in natural conditions. Affine transformations are particularly relevant for study, as they are among the most commonly encountered by human observers in everyday life. This Data Descriptor presents a set of human responses to suprathreshold affine image transformations (rotation, translation, scaling) and Gaussian noise as convenient reference to compare with existing image quality datasets. The responses were measured using well-established psychophysics: the Maximum Likelihood Difference Scaling (MLDS). The set contains responses to 864 distorted images. The experiments involved 210 observers and over 40,000 image quadruple comparisons. The dataset is validated by two facts: (a) the responses reproduce classical absolute detection thresholds of the affine and Gaussian distortions, and (b) the responses to Gaussian distortion are correlated to the Mean Opinion Score (MOS) of conventional image quality databases for that distortion. Moreover, the classical Piéron’s law applies to the reaction times of the dataset, and Group-MAD adversarial stimuli reveal that MLDS perceptual scales are more accurate than the conventional MOS.
Similar content being viewed by others
Data availability
The dataset and accompanying materials are publicly available on Zenodo at [https://doi.org/10.5281/zenodo.17348027]38, ensuring long-term preservation, accessibility, and reproducibility. All data are released under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.
Code availability
The source code supporting this work is available on GitHub at [https://github.com/paudauo/BBDD_Affine_Transformations], where detailed documentation is provided in the README file. Together with the dataset, we provide coding examples in Python. In particular, we show how to read the different versions of the dataset. We also demonstrate how to read the raw data specifically and compute the MLDS perceptual scales for a single image and a single distortion. Other libraries could be used to compute the MLDS perceptual scales, such as the one from the original authors46, or a wrapper to use it in Python47. Additionally, we provide an example of reading the MLDS perceptual scales already computed for all images and all distortions. We also show how to convert the MLDS data to MOS values.
The structure of the code is as follows:
• Load_DDBB_example.ipynb: Load images and responses.
• Load_RAW_data_and_compute_MLDS.ipynb: Compute MLDS curves from raw data.
• Load_MLDS_data_and_plot_curves.ipynb: Plot normalized perceptual scale curves.
• Convert_MLDS_to_MOS.ipynb: Convert MLDS perceptual scales to MOS (aligned with TID2013).
• Load_RAW_data_and_plot_left_right_RT.ipynb: Analyze reaction times and decision patterns.
References
Wang, Z. & C. Bovik, A. Mean squared error: Love it or leave it? a new look at signal fidelity measures. IEEE Signal Processing Magazine 26, 98–117, https://doi.org/10.1109/MSP.2008.930649 (2009).
Zhang, R., Isola, P., Efros, A. A., Shechtman, E. & Wang, O. The unreasonable effectiveness of deep features as a perceptual metric, in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 586–595, https://doi.org/10.1109/CVPR.2018.00068 (2018).
Watson, A. & Malo, J. Video quality measures based on the standard spatial observer, in Proceedings. International Conference on Image Processing, vol. 3, pp. III–III, https://doi.org/10.1109/ICIP.2002.1038898 (2002).
Laparra, V., Munoz-Marí, J. & Malo, J. Divisive normalization image quality metric revisited. J. Opt. Soc. Am. A 27, 852–864, https://doi.org/10.1364/JOSAA.27.000852 (2010).
Hepburn, A., Laparra, V., Malo, J., McConville, R. & Santos-Rodriguez, R. Perceptnet: A human visual system inspired neural network for estimating perceptual distance, in 2020 IEEE International Conference on Image Processing (ICIP), pp. 121–125, https://doi.org/10.1109/ICIP40778.2020.9190691 (2020).
Laparra, V., Berardino, A., Ballé, J. & Simoncelli, E. P. Perceptually optimized image rendering. J. Opt. Soc. Am. A 34, 1511–1525, https://doi.org/10.1364/JOSAA.34.001511 (2017).
Martinez-Garcia, M., Cyriac, P., Batard, T., Bertalmío, M. & Malo, J. Derivatives and inverse of cascaded linear+nonlinear neural models. PLoS ONE 13, e0201326, https://doi.org/10.1371/journal.pone.0201326 (2018).
Kumar, M., Houlsby, N., Kalchbrenner, N. & Cubuk, E. D. Do better imagenet classifiers assess perceptual similarity better?, Transactions on Machine Learning Research (2022).
Hernández-Cámara, P., Vila-Tomás, J., Laparra, V. & Malo, J. Dissecting the effectiveness of deep features as metric of perceptual image quality. Neural Networks 185, 107189, https://doi.org/10.1016/j.neunet.2025.107189 (2025).
Martinez-Garcia, M., Bertalmío, M. & Malo, J. In praise of artifice reloaded: Caution with natural image databases in modeling vision, Frontiers in Neuroscience 13, https://doi.org/10.3389/fnins.2019.00008 (2019).
Lin, H., Hosu, V. & Saupe, D. Kadid-10k: A large-scale artificially distorted iqa database, in 2019 Tenth International Conference on Quality of Multimedia Experience (QoMEX), pp. 1–3, IEEE, (2019).
Gu, J. et al. Pipal: a large-scale image quality assessment dataset for perceptual image restoration, in European Conference on Computer Vision (ECCV) 2020, pp. 633–651, Springer, https://doi.org/10.1007/978-3-030-58621-8_37 (2020).
Ponomarenko, N. et al. Image database TID2013: Peculiarities, results and perspectives. Signal Processing: Image Communication 30, 57–77, https://doi.org/10.1016/j.image.2014.10.009 (2015).
Torralba, A., Isola, P. & Freeman, W. Foundations of Computer Vision, MIT Press, (2024).
Liu, X., Pedersen, M. & Hardeberg, J. Y. Cid:iq – a new image quality database, in Image and Signal Processing, pp. 193–202, Springer, https://doi.org/10.1007/978-3-319-07998-1_22 (2014).
Abrams, A. B., Hillis, J. M. & Brainard, D. H. The relation between color discrimination and color constancy: When is optimal adaptation task dependent? Neural Computation 19, 2610–2637, https://doi.org/10.1162/neco.2007.19.10.2610 (2007).
Chromatic Adaptation Models, chap. 9, pp. 181–198, John Wiley & Sons, Ltd, (2013).
Laparra, V., Jiménez, S., Camps-Valls, G. & Malo, J. Nonlinearities and adaptation of color vision from sequential principal curves analysis. Neural Computation 24, 2751–2788, https://doi.org/10.1162/NECO_a_00342 (2012).
Atherton, T. Energy and phase orientation mechanisms: a computational model. Spatial Vision 15, 415–441, https://doi.org/10.1163/156856802320401892 (2002).
Todorović, D. Extension of a computational model of a class of orientation illusions. Vision Research 223, 108459, https://doi.org/10.1016/j.visres.2024.108459 (2024).
Frisby, J. P. & Stone, J. V. Seeing: The computational approach to biological vision, MIT Press, (2010).
Hansard, M. & Horaud, R. A differential model of the complex cell. Neural Computation 23, 2324–2357, https://doi.org/10.1162/NECO_a_00163 (2011).
Langley, K., Lefebvre, V. & Anderson, S. J. Cascaded bayesian processes: An account of bias in orientation perception. Vision Research 49, 2453–2474, https://doi.org/10.1016/j.visres.2009.07.015 (2009).
Bruna, J. & Mallat, S. Invariant scattering convolution networks. IEEE Transactions on Pattern Analysis and Machine Intelligence 35, 1872–1886, https://doi.org/10.1109/TPAMI.2012.230 (2013).
Bouvrie, J., Rosasco, L. & Poggio, T. On invariance in hierarchical models, in Advances in Neural Information Processing Systems, vol. 22, Curran Associates, (2009).
Alabau-Bosque, N., Daudén-Oliver, P., Vila-Tomás, J., Laparra, V. & Malo, J. Invariance of deep image quality metrics to affine transformations, https://doi.org/10.48550/arXiv.2407.17927 (2024).
International Telecommunication Union (ITU), Recommendation ITU-R BT.500-13: Methodology for the subjective assessment of the quality of television pictures, Tech. Rep., (2012).
Kingdom, F. A. & Prins, N. Psychophysics, 2nd ed., Academic Press, UK, (2016).
Maloney, L. T. & Yang, J. N. Maximum likelihood difference scaling. Journal of Vision 3, 5–5, https://doi.org/10.1167/3.8.5 (2003).
Ma, K. et al. Group maximum differentiation competition: Model comparison with few samples. IEEE Transactions on Pattern Analysis and Machine Intelligence 42, 851–864, https://doi.org/10.1109/TPAMI.2018.2889948 (2020).
Eastman Kodak Company, Kodak lossless true color image suite, 1999. https://r0k.us/graphics/kodak/.
Piéron, H. II. recherches sur les lois de variation des temps de latence sensorielle en fonction des intensités excitatrices. L’année psychologique 20, 17–96 (1913).
Daly, S. Application of a Noise Adaptive Contrast Sensitivity Function to Image Data Compression, in Human Vision, Visual Processing, and Digital Display, vol. 1077, pp. 217–227, SPIE, https://doi.org/10.1117/12.952720 (1989).
Wagenmakers, E.-J. & Brown, S. On the linear relation between the mean and the standard deviation of a response time distribution. Psychological Review 114, 830–841, https://doi.org/10.1037/0033-295x.114.3.830 (2007).
Kepecs, A., Uchida, N., Zariwala, H. A. & Mainen, Z. F. Neural correlates, computation and behavioural impact of decision confidence. Nature 455, 227–231, https://doi.org/10.1038/nature07200 (2008).
Wang, Z. & Simoncelli, E. P. Maximum differentiation (MAD) competition: A methodology for comparing computational models of perceptual quantities. Journal of Vision 8, 8–8, https://doi.org/10.1167/8.12.8 (2008).
Malo, J. & Simoncelli, E. P. Geometrical and statistical properties of vision models obtained via maximum differentiation, in Proc SPIE Conf on Human Vision and Electronic Imaging (HVEI XX), vol. 9394, Optical Society of America, https://doi.org/10.1117/12.2085653 (2015).
Daudén-Oliver, P. et al. RAID-Dataset: human responses to affine image distortions and Gaussian noise, https://doi.org/10.5281/zenodo.17348027 (2025).
Regan, D., Gray, R. & Hamstra, S. Evidence for a neural mechanism that encodes angles. Vision Research 36, 323–IN3, https://doi.org/10.1016/0042-6989(95)00113-E (1996).
Legge, G. E. & Campbell, F. Displacement detection in human vision. Vision Research 21, 205–213, https://doi.org/10.1016/0042-6989(81)90114-0 (1981).
Baldwin, A., Fu, M., Farivar, R. & Hess, R. The equivalent internal orientation and position noise for contour integration. Scientific Reports 7, 2045–2322, https://doi.org/10.1038/s41598-017-13244-z (2017).
Teghtsoonian, R. On the exponents in Stevens’ law and the constant in Ekman’s law, Psychological Review, https://doi.org/10.1037/h0030300 (1971).
Aguilar, G., Wichmann, F. A. & Maertens, M. Comparing sensitivity estimates from MLDS and forced-choice methods in a slant-from-texture experiment. Journal of Vision 17, 37–37, https://doi.org/10.1167/17.1.37 (2017).
Devinck, F. & Knoblauch, K. A common signal detection model accounts for both perception and discrimination of the watercolor effect. Journal of Vision 12, 19–19, https://doi.org/10.1167/12.3.19 (2012).
Campbell, F. W. & Robson, J. G. Application of Fourier analysis to the visibility of gratings. Journal of Physiology 197, 551–566, https://doi.org/10.1113/jphysiol.1968.sp008574 (1968).
Knoblauch, K. & Maloney, L. T. MLDS: Maximum likelihood difference scaling in R. Journal of Statistical Software 25, 1–26, https://doi.org/10.18637/jss.v025.i02 (2008).
Aguilar, G. Python wrapper for MLDS R package, https://github.com/computational-psychology/mlds (2022).
Acknowledgements
This work was partially funded by the Valencian local government (GVA) under the grant CIGE/2022/066 (grupos emergentes), by the Universitat Jaume I (UJI) under the grant UJI-A2022-12, by the Ministerio de Ciencia e Innovación grants number PID2020-118071GB-I00 and PDC2021-121522-C21, PID2023-152133NB-I00, and by the grant BBVA Foundations of Science program: Mathematics, Statistics, Computational Sciences and Artificial Intelligence (VIS4NN).
Author information
Authors and Affiliations
Contributions
P.D. - data acquisition, data processing, validation, writing. D.A. - data acquisition, data processing, validation. E.S. - software development, data acquisition, writing. R.M. - writing. V.L - data processing, validation, writing. J.M. - writing, validation. M.M. - data acquisition, validation, writing. All authors read, edited, and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Daudén-Oliver, P., Agost-Beltran, D., Sansano-Sansano, E. et al. RAID-Dataset: human responses to affine image distortions and Gaussian noise. Sci Data (2026). https://doi.org/10.1038/s41597-026-06581-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-026-06581-0