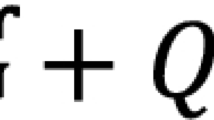Improved modified estimator for estimation of median using auxiliary information under simple random sampling

Abstract

This article aims to suggest an improved estimator for estimation of population median using auxiliary information under simple random sampling. The expression for the bias and mean square error are obtained up to first order approximation. We determine the MLE of the optimal values of the describing scalars. The proficiency of the suggested estimator is evaluated in comparison to the preliminary estimators using the MSE threshold. The suggested estimators are compared numerically to the ones that are currently studied in this study. The performance and novelty of the estimators was evaluated using real data sets and a simulation study. To check the efficiency of estimators empirical and theoretical study has been studied. Based on numerical result it is to be noted that our suggested estimator is more efficient as compared to existing estimators which is considered in this article in terms of least MSE and greater PRE.

Introduction

In survey sampling, utilization of auxiliary information can improved estimator efficiency whichever at the design or at the estimation stage. Many efforts have been done for the purpose of increasing efficiency of an estimator. The efficient estimators of the population’s median have received comparatively less attention compared to that of its mean, proportion, variance, regression coefficient, etc., which have all been the subject of significant studies. Income, expenditure, taxation, consumption, and production are frequently of interest to researchers; at this point the distributions of these last two variables are extremely skewed. The median is a far better, rather than the mean in these circumstances. It is common for statisticians to be interested in handling variables with extremely skewed distributions, such earnings and consumption, in the sampling literature. In such circumstances, the median is believed to be a well central measure than the mean. The authors in Ref.¹ recommended enhanced estimator for median exhausting auxiliary information under simple and stratified random sampling. Reference² discussed difference type estimator for median estimation. The authors in Refs.^3,4,5 discussed estimation of population median using two phase sampling. Reference⁶ recommended median estimator using auxiliary information. Reference⁷ suggested improved estimator for population median. References^8,9 discussed a novel estimator utilizing auxiliary information. Reference¹⁰ recommend ratio and regression type estimator for population median. Reference¹¹ suggested enhanced estimator for population median usig two phase sampling. The authors in Refs.^12,13 discussed exponential and ratio type estimator for population median. Reference¹⁴ discussed difference type estimator for population median using auxiliary information. The authors in Refs.^{15,16,17,18,19,20,21,22,23,24} discussed some improved estimator for population parameter under different sampling design using auxiliary information.

Materials and methods

Let a population consists $\text{W}$ = $\left({\text{W}}_{1}, {\text{W}}_{2}, \dots , {\text{W}}_{N}\right)$ of N differing units. Let $Y_{i}$ and $X_{i}$ be the $i{\text{th}}$ values of the study variable and the auxiliary variables. Let a sample of n is chosen from $\text{W}$. The sample and population medians of the study and the auxiliary variable are denoted by $M_{y}$ and $M_{x}$, and $M_{y}$ and $M_{x}$ with probability density functions of fy $\left({M}_{y}\right)$ and fx $\left({M}_{x}\right)$. The correlation coefficienct between the $M_{y}$ and $M_{x}$ are represented by ${\rho }_{yx}$ and is defined as ${\rho }_{\left({M}_{y}, {M}_{x}\right)}$ = 4 ${P}_{11}\left(y,x\right) -$ 1, where ${P}_{11}$ = $P\left(y\le {M}_{y}\cap x\le {M}_{x}\right)$.

To gain the expressions of bias and MSE we used the following error terms:

$${{e}_{y}}=\left(\frac{{{\widehat{M}}_{y}}-{{M}_{y}}}{{M}_{y}}\right), \text{ and }{{e}_{x}}=\left(\frac{{{\widehat{M}}_{x}}-{{M}_{x}}}{{M}_{x}}\right),$$

$${\text{E}}\left({e}_{y}^{2}\right)= \lambda {C}_{My}^{2},\text{ E}\left({e}_{x}^{2}\right)= \lambda {C}_{Mx}^{2}, {\text{E}}\left({e}_{y}\,{e}_{x} \right)=\lambda {C}_{Myx}^{2},$$

where

$${C}_{My}=\frac{1}{{M}_{y}\left({M}_{y}\right)}, {C}_{Mx}=\frac{1}{{M}_{x}{f}_{x}\left({M}_{x}\right)}, {C}_{Myx }={\rho }_{yx}{C}_{My}{C}_{Mx},\Lambda =\left(\frac{1}{4}\left\{\frac{1}{n}-\frac{1}{N}\right\}\right).$$

Existing counterparts

This section consists of some well know existing estimators for comparison purpose.

• (1) Reference⁶ discuss usual unbiased median estimator $\left({\widehat{M}}_{y}\right)$, which is given by:

  $${\widehat{M}}_{y}={\widetilde{M}}_{y}.$$

  (1)

  The variance of ${\widehat{M}}_{y}$, is given by:

  $$ Var\left( {\hat{M}_{y} } \right) = \Lambda M_{y}^{2} C_{My}^{2} = \Lambda \left\{ {f_{y} (M_{y} )} \right\}^{ - 2} . $$

  (2)

• (2) Reference⁹ recommended ratio estimator, which is given by:

  $$ \hat{M}_{R} = \hat{M}_{y} \left( {\frac{{M_{x} }}{{M_{x} }}} \right). $$

  (3)

  The expressions of $Bias\left( {\hat{M}_{R} } \right)$ and $MSE\left( {\hat{M}_{R} } \right)$ are given by:

  $$ Bias\left( {\hat{M}_{R} } \right) \cong \Lambda M_{y} \left( {C_{Mx}^{2} - C_{Myx} } \right), $$
  $$ MSE\left( {\hat{M}_{R} } \right) \cong \Lambda M_{y}^{2} \left( {C_{My}^{2} + C_{Mx}^{2} - 2C_{Myx} } \right). $$

  (4)

• (3) The exponential ratio-type estimator is given by:

  $$ \hat{M}_{EX} = \hat{M}_{y} \exp \left( {\frac{{M_{x} - \hat{M}_{x} }}{{M_{x} + \hat{M}_{x} }}} \right). $$

  (5)

  The expressions of $Bias\left( {\hat{M}_{EX} } \right)$ and $MSE\left( {\hat{M}_{EX} } \right)$ are given by

  $$ Bias\left( {\hat{M}_{EX} } \right) \cong \Lambda M_{y} \left( {\frac{3}{8}C_{Mx}^{2} - \frac{1}{2}C_{Myx} } \right), $$

  and

  $$ MSE\left( {\hat{M}_{EX} } \right) \cong \Lambda M_{y}^{2} \left( {C_{My}^{2} + \frac{1}{4}C_{Mx}^{2} - 2C_{Myx} } \right){.} $$

  (6)

• (4) The difference estimator, is given by:

  $$ \hat{M}_{D} = \hat{M}_{y} + d\left( {M_{x} - \hat{M}_{x} } \right){.} $$

  (7)

  The optimum value of d is given by:

  $$ d_{opt} = \frac{{M_{y} \rho_{yx} C_{My} }}{{M_{x} C_{Mx} }}. $$

  The minimum $MSE\left( {\hat{M}_{D} } \right)$ at the optimum value is given by:

  $$ MSE\left( {\hat{M}_{D} } \right)_{\min } \cong \Lambda M_{y}^{2} C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right){.} $$

  (8)

• (5) Following^5,10,25 respectively, proposed some difference-type estimators $\hat{M}_{Di} (i = 1,2,3)$, which is given by:

  $$ \hat{M}_{D1} = d_{1} \hat{M}_{y} + d_{2} \left( {M_{x} - \hat{M}_{x} } \right){,} $$

  (9)
  $$ \hat{M}_{D2} = \left[ {d_{3} \hat{M}_{y} + d_{4} \left( {M_{x} - \hat{M}_{x} } \right)} \right]\left( {\frac{{M_{x} }}{{\hat{M}_{x} }}} \right), $$

  (10)
  $$ \hat{M}_{D3} = \left[ {d_{5} \hat{M}_{y} + d_{6} \left( {M_{x} - \hat{M}_{x} } \right)} \right]\exp \left( {\frac{{M_{x} - \hat{M}_{x} }}{{M_{x} + \hat{M}_{x} }}} \right){.} $$

  (11)

  At the optimum values of $d_{i} (i = 1,2,.....,6)$ the bias of $\hat{M}_{Di} (i = 1,2,3)$ are given by

  $$ Bias\left( {\hat{M}_{D1} } \right) \cong M_{y} \left( {d_{1} - 1} \right){,} $$
  $$ Bias\left( {\hat{M}_{D2} } \right) \cong M_{y} \left( {d_{3} - 1} \right) + d_{3} \Lambda M_{y} \left( {C_{Mx}^{2} - C_{Myx} } \right) + d_{4} \Lambda M_{x} C_{Mx}^{2} {,} $$
  $$ Bias\left( {\hat{M}_{D3} } \right) \cong M_{y} \left( {d_{5} - 1} \right) + d_{5} \Lambda M_{y} \left\{ {\frac{3}{8}C_{Mx}^{2} - \frac{1}{2}C_{Myx} } \right\} + \frac{1}{2}d_{6} \Lambda M_{x} C_{Mx}^{2} . $$

  At the optimum values of $d_{i} (i = 1,2,...,6)$

  $$ d_{1(opt)} = \frac{1}{{1 + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}},\;d_{5(opt)} = \frac{{1 - \left( {{{\Lambda C_{Mx}^{2} } \mathord{\left/ {\vphantom {{\Lambda C_{Mx}^{2} } 8}} \right. \kern-0pt} 8}} \right)}}{{1 + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}, $$
  $$ d_{3(opt)} = \frac{{1 - \Lambda C_{Mx}^{2} }}{{1 - \Lambda C_{Mx}^{2} + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}},\;d_{2(opt)} = \frac{{M_{y} }}{{M_{x} }}\left[ {\frac{{\rho_{xy} C_{My} }}{{C_{Mx} \left\{ {1 + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)} \right\}}}} \right], $$
  $$ d_{4(opt)} = \frac{{M_{y} }}{{M_{x} }}\left[ {1 + d_{3(opt)} \left( {\frac{{\rho_{xy} C_{My} }}{{C_{Mx} }} - 2} \right)} \right]\;{\text{and}}\;d_{6(opt)} = \frac{{M_{y} }}{{M_{x} }}\left[ {\frac{1}{2} + d_{5(opt)} \left( {\frac{{\rho_{xy} C_{My} }}{{C_{Mx} }} - 1} \right)} \right]. $$

  The minimum mean square error of $\hat{M}_{Di} (i = 1,2,3)$ are given by

  $$ MSE\left( {\hat{M}_{D1} } \right)_{\min } \cong \frac{{\Lambda M_{y}^{2} C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}{{1 + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}, $$

  (12)
  $$ MSE\left( {\hat{M}_{D2} } \right)_{\min } \cong \frac{{\Lambda M_{y}^{2} \left( {1 - \Lambda C_{Mx}^{2} } \right)C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}{{\left( {1 - \Lambda C_{Mx}^{2} } \right) + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}{,} $$

  (13)
  $$ MSE\left( {\hat{M}_{D3} } \right)_{\min } \cong \frac{{\Lambda M_{y}^{2} \left[ {C_{Mx}^{2} \left( {1 - \rho_{xy}^{2} } \right) - \frac{\Lambda }{4}C_{Mx}^{2} \left\{ {\frac{1}{16}C_{Mx}^{2} + C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)} \right\}} \right]}}{{1 + \Lambda C_{My}^{2} \left( {1 - \rho_{xy}^{2} } \right)}}. $$

  (14)

• (6) Reference¹⁴ suggested the generalized difference-type estimator for population median, which is given by:

  $$ \hat{M}^{G}_{pp} = \left[ {m_{1} \hat{M}_{y} + m_{2} \left( {M_{x} - \hat{M}_{x} } \right)} \right]\left[ {\left( {\frac{{aM_{x} + b}}{{a\hat{M}_{x} + b}}} \right)\exp \left\{ {\frac{{\alpha_{2} a\left( {M_{x} - \hat{M}_{x} } \right)}}{{a\left\{ {(\gamma - 1)M_{x} + \hat{M}_{x} } \right\} + 2b}}} \right\}} \right], $$

  (15)

  where $m_{1}$ and $m_{2}$ are unidentified constants whose values are to be determined, $a$ and $b$ defined as unknown population parameters and $\alpha_{1}$, $\alpha_{2}$ and $\gamma$ are scalar quantities which can take different values like $\alpha_{1} = b = 0$ and $\alpha_{2} = \gamma = a = 1$.

  The $Bias\left( {\hat{M}^{G}_{pp} } \right)$ is given by

  $$ Bias\left( {\hat{M}_{pp}^{G} } \right) \cong (m_{1} - 1)M_{y} + m_{2} M_{y} \Lambda \left\{ {\frac{3}{2}C_{Mx}^{2} - C_{My} } \right\} + m_{2} M_{x} \Lambda C_{Mx}^{2} {.} $$

  At the optimum values of

  $$ m_{1(opt)} = \frac{{1 - 0.5\Lambda C_{Mx}^{2} }}{{1 + \Lambda C_{My}^{2} (1 - \rho_{xy}^{2} )}}, $$

  and

  $$ m_{2(opt)} = \frac{{M_{y} }}{{M_{x} }}\left[ {1 + m_{1(opt)} \left\{ {\frac{{\rho_{xy} C_{My} }}{{C_{Mx} }} - 2} \right\}} \right]. $$

  The $\min MSE\left( {\hat{M}^{G}_{pp} } \right)$ is given by

  $$ MSE\left( {\hat{M}^{G}_{pp} } \right)_{\min } \cong \frac{{M_{y}^{2} }}{{1 + \Lambda C_{My}^{2} (1 - \rho_{xy}^{2} )}}\left[ {\Lambda C_{My}^{2} (1 - \rho_{xy}^{2} ) - \frac{1}{4}\Lambda^{2} C_{Mx}^{4} - \Lambda^{2} C_{My}^{2} C_{Mx}^{2} (1 - \rho_{xy}^{2} )} \right]{.} $$

  (16)

• (7) The author in Ref.² proposed the following difference type estimator using two-auxiliary variables

  $$ \hat{M}_{P}^{I} = \left\{ {\hat{M}_{y} + m_{1} \left( {M_{x} - \hat{M}_{x} } \right)} \right\}\left\{ {m_{2} \exp \left( {\frac{{M_{z} - \hat{M}_{z} }}{{M_{z} + \hat{M}_{z} }}} \right)} \right.\left. { + \left( {1 - m_{2} } \right)\exp \left( {\frac{{\hat{M}_{z} - M_{z} }}{{M_{z} + \hat{M}_{z} }}} \right)} \right\}{.} $$

  (17)

  The $Bias\left( {\hat{M}_{P}^{I} } \right)$ is given by

  $$ Bias\left( {\hat{M}_{P}^{I} } \right) = \Lambda \left[ {m_{1} M_{x} C_{Mxz} \left( {m_{2} - 0.5} \right) + M_{y} C_{Myz} \left( {0.5 - m_{2} } \right)} \right]. $$

  The $MSE\left( {\hat{M}_{P}^{I} } \right)$ is given by

  $$ MSE\left( {\hat{M}_{P}^{I} } \right) = \Lambda \left[ {M_{y}^{2} } \right.\left\{ {\left( {C_{My}^{2} + 0.25C_{Mz}^{2} } \right) + m_{2} C_{Mz} \left( {m_{2} } \right.C_{Mz} - C_{Mz} - 2\rho_{yz} \left. {C_{My} } \right) + \rho_{yz} C_{My} C_{Mz} } \right\} + m_{1} M_{x} C_{Mx} \left( {m_{1} } \right.\,M_{x} C_{Mx} - 2M_{y} \rho_{yx} C_{My} - \rho_{xz} C_{Mz} M_{y} + 2m_{2} \rho_{xz} C_{Mz} \left. {\left. {M_{y} } \right)} \right], $$
  $$ m_{1(opt)} = \frac{{C_{My} M_{y} \left( {\rho_{xz} \rho_{yz} - \rho_{yx} } \right)}}{{C_{Mx} M_{x} \left( {\rho_{xz}^{2} - 1} \right)}}, $$
  $$ m_{2(opt)} = \frac{{C_{Mz} \left( {\rho_{xz}^{2} - 1} \right) + 2C_{My} \left( {\rho_{xz} \rho_{yx} - \rho_{yz} } \right)}}{{2C_{Mz} \left( {\rho_{xz}^{2} - 1} \right)}}. $$

  At the optimum values of, the expression of $MSE(M_{p}^{I} )_{\min }$ is given by:

  $$ MSE(\hat{M}_{p}^{I} )_{\min } = \frac{{\Lambda M_{y}^{2} C_{My}^{2} }}{{\left( {1 - \rho_{xz}^{2} } \right)}}\left( {1 - \rho_{xz}^{2} - \rho_{yx}^{2} - \rho_{yz}^{2} + 2\rho_{yx} \rho_{xz} \rho_{yz} } \right). $$

  (18)

• (8) Reference²⁶ proposed the following ratio-cum-product exponential-type median estimator as

  $$ \hat{M}_{SM} = \hat{M}_{y} \left\{ {m_{12} \left( {\frac{{M_{x} }}{{\hat{M}_{x} }}} \right)} \right.\left. { + m_{13} \left( {\frac{{\hat{M}_{x} }}{{M_{x} }}} \right)} \right\}\left\{ {\alpha \exp \left( {\frac{{M_{x} - \hat{M}_{x} }}{{M_{x} + \hat{M}_{x} }}} \right)} \right.\left. { + \left( {1 - \alpha } \right)\exp \left( {\frac{{\hat{M}_{x} - M_{x} }}{{M_{x} + \hat{M}_{x} }}} \right)} \right\}{,} $$

  (19)
  $$ Bias\left( {\hat{M}_{SM} } \right) = M_{y} \left[ {\left( {m_{12} + m_{13} - 1} \right) + m_{12} \Lambda \left\{ {\left( {\frac{3}{8} + \frac{3\alpha }{2}} \right)C_{Mx}^{2} - \left( {\alpha + \frac{1}{2}} \right)C_{Myx} } \right\}} \right.\left. { + m_{13} \Lambda \left\{ {\left( {\frac{3}{2} - \alpha } \right)C_{Myx} + \left( {\frac{3}{8} - \frac{\alpha }{2}} \right)C_{Mx}^{2} } \right\}} \right]. $$

The optimal values of $m_{12(opt)} = \left[ {\frac{{A_{2} A_{4} - A_{3} A_{5} }}{{A_{1} A_{2} - A_{3}^{2} }}} \right]$ and $m_{13(opt)} = \left[ {\frac{{A_{1} A_{5} - A_{3} A_{4} }}{{A_{1} A_{2} - A_{3}^{2} }}} \right]$, the expression of $MSE\left( {M_{SM} } \right)_{\min }$ is given by:

$$ MSE\left( {M_{SM} } \right)_{\min } = M_{y}^{2} \left[ {1 - \frac{{A_{1} A_{5}^{2} - 2A_{3} A_{4} A_{5} + A_{2} A_{4}^{2} }}{{A_{1} A_{2} - A_{3}^{2} }}} \right], $$

(20)

where $A_{1} = 1 + \Lambda \left\{ {C_{My}^{2} + \left( {\alpha^{2} + 4\alpha + 1} \right)C_{Mx}^{2} - 2\left( {2\alpha + 1} \right)C_{Myx} } \right\},$ $A_{2} = 1 + \Lambda \left\{ {C_{My}^{2} + \left( {\alpha^{2} - 4\alpha + 3} \right)C_{Mx}^{2} + 2\left( {3 - 2\alpha } \right)C_{Myx} } \right\},$ $A_{3} = 1 + \Lambda \left\{ {C_{My}^{2} + 2\left( {1 - 2\alpha } \right)C_{Myx} + \alpha^{2} C_{Mx}^{2} } \right\},$ $A_{4} = 1 + \Lambda \left\{ {\left( {\frac{3}{8} + \frac{3\alpha }{2}} \right)C_{Mx}^{2} - \left( {\alpha + \frac{1}{2}} \right)C_{Myx} } \right\}$ and $A_{5} = 1 + \Lambda \left\{ {\left( {\frac{3}{8} - \frac{\alpha }{2}} \right)C_{Mx}^{2} + \left( {\frac{3}{2} - \alpha } \right)C_{Myx} } \right\}$.

Proposed estimator

Estimator performance can be enhanced by making use of auxiliary information during design and estimation stages. We used auxiliary information to determine the population median based on this notion. Taking motivation from Ref.²⁷, we have suggested an improved estimator for population median using single auxiliary variable under simple random sampling. Our suggested estimator under simple random sampling offers several advantages over the existing estimators, the most notable of which are their enhanced adaptability, efficiency, and originality, which is given by:

$$ \hat{M}_{y}^{*} = \left[ {\alpha_{1} \hat{M}_{y} \left\{ {\frac{1}{2}\left( {\frac{{M_{x} }}{{\hat{M}_{x} }} + \frac{{\hat{M}_{x} }}{{M_{x} }}} \right)} \right\} + \alpha_{2} \left( {M_{x} - \hat{M}_{x} } \right)} \right]\exp \left( {\frac{{M_{x} - \hat{M}_{x} }}{{M_{x} + \hat{M}_{x} }}} \right). $$

(21)

By expressing the above equation in error terms, we have:

$$ \hat{M}_{y}^{*} = \left[ {\alpha_{1} M_{y} (1 + e_{y} )\left\{ {\frac{1}{2}\left( {(1 + e_{x} )^{ - 1} + 1 + e_{x} } \right)} \right\} + \alpha_{2} \left( {M_{x} - M_{x} (1 + e_{x} )} \right)} \right]\exp \left( {\frac{{M_{x} - M_{x} (1 + e_{x} )}}{{M_{x} + M_{x} (1 + e_{x} )}}} \right). $$

After simplifying we have:

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} + \frac{{e_{x}^{2} }}{2}} \right\} - \alpha_{2} M_{x} e_{x} } \right]\exp \left( {\frac{{ - e_{x} }}{{2 + e_{x} }}} \right) - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} + \frac{{e_{x}^{2} }}{2}} \right\} - \alpha_{2} M_{x} e_{x} } \right]\exp \left\{ {\frac{{ - e_{x} }}{2}\left( {1 - \frac{{e_{x} }}{2} + \frac{{e_{x}^{2} }}{4}} \right)} \right\} - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} + \frac{{e_{x}^{2} }}{2}} \right\} - \alpha_{2} M_{x} e_{x} } \right]\exp \left\{ {\left( {\frac{{e_{x}^{2} }}{4} - \frac{{e_{x} }}{2}} \right)} \right\} - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} + \frac{{e_{x}^{2} }}{2}} \right\} - \alpha_{2} M_{x} e_{x} } \right]\left( {1 - \frac{{e_{x} }}{2} + \frac{{3e_{x}^{2} }}{8}} \right) - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} + \frac{{e_{x}^{2} }}{2}} \right\}\left( {1 - \frac{{e_{x} }}{2} + \frac{{3e_{x}^{2} }}{8}} \right) - \alpha_{2} M_{x} \left( {e_{x} - \frac{{e_{x}^{2} }}{2}} \right)} \right] - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1\left( {1 - \frac{{e_{x} }}{2} + \frac{{3e_{x}^{2} }}{8}} \right) + e_{y} \left( {1 - \frac{{e_{x} }}{2} + \frac{{3e_{x}^{2} }}{8}} \right) + \frac{{e_{x}^{2} }}{2}\left( {1 - \frac{{e_{x} }}{2} + \frac{{3e_{x}^{2} }}{8}} \right)} \right\} - \alpha_{2} M_{x} \left( {e_{x} - \frac{{e_{x}^{2} }}{2}} \right)} \right] - M_{y} , $$

$$ \hat{M}_{y}^{*} - M_{y} = \left[ {\alpha_{1} M_{y} \left\{ {1 + e_{y} - \frac{{e_{x} }}{2} + \frac{{7e_{x}^{2} }}{8} - \frac{{e_{x} e_{y} }}{2}} \right\} - \alpha_{2} M_{x} \left( {e_{x} - \frac{{e_{x}^{2} }}{2}} \right)} \right] - M_{y} , $$

$${M}_{y}^{*}-{M}_{y}=\left({\alpha }_{1}\times {M}_{y}\times \left(1+{e}_{y}-\frac{{e}_{x}}{2}+\frac{7\times {e}_{x}\times {e}_{x}}{8}-\frac{{e}_{x}\times {e}_{y}}{2}\right)+{\alpha }_{2}\times {M}_{x}\times \left(\frac{{e}_{x}\times {e}_{x}}{2}-{e}_{x}\right)-{M}_{y}\right).$$

(22)

Taking expectation on both sides of Eq. (22), we have:

$${Bias(M}_{\text{y}}^{*})=E\left[{\alpha }_{1}\times {M}_{y}\times \left(1+{e}_{y}-\frac{{e}_{x}}{2}+\frac{7\times {e}_{x}\times {e}_{x}}{8}-\frac{{e}_{x}\times {e}_{y}}{2}\right)+{\alpha }_{2}\times {M}_{x}\times \left(\frac{{e}_{x}\times {e}_{x}}{2}-{e}_{x}\right)-{M}_{y}\right],$$

$$\text{Bias}\left({M}_{\text{y}}^{*}\right)=\left[{\alpha }_{1}\times {M}_{y}\times \left(1+\frac{7\times \varphi \times {C}_{x}^{2}}{8}-\frac{\varphi \times {R}_{\text{yx}}{C}_{y}{C}_{x}}{2}\right)+{\alpha }_{2}\times {M}_{x}\times \left(\frac{\varphi \times {C}_{x}^{2}}{2}\right)-{M}_{y}\right].$$

Squaring Eq. (22), and ignoring higher order terms and taking expectation, we got:

$$\text{MSE}\left({M}_{\text{y}}^{*}\right)=E{\left[{\alpha }_{1}\times {M}_{y}\times \left(1+{e}_{y}-\frac{{e}_{x}}{2}+\frac{7\times {e}_{x}\times {e}_{x}}{8}-\frac{{e}_{x}\times {e}_{y}}{2}\right)+{\alpha }_{2}\times {M}_{x}\times \left(\frac{{e}_{x}\times {e}_{x}}{2}-{e}_{x}\right)-{M}_{y}\right]}^{2},$$

$$\text{MSE}\left({M}_{\text{y}}^{*}\right)=\left[{M}_{y}^{2}-2{M}_{y}^{2}{\alpha }_{1}-\frac{7}{4}{e}_{x}^{2}{M}_{y}^{2}{\alpha }_{1}+{e}_{x}{e}_{y}{M}_{y}^{2}{\alpha }_{1}+{M}_{y}^{2}{\alpha }_{1}^{2}+2{e}_{x}^{2}{M}_{y}^{2}{\alpha }_{1}^{2}-2{e}_{x}{e}_{y}{M}_{y}^{2}{\alpha }_{1}^{2}+{e}_{y}^{2}{M}_{y}^{2}{\alpha }_{1}^{2}-{e}_{x}^{2}{M}_{x}{M}_{y}{\alpha }_{2}+2{e}_{x}^{2}{M}_{x}{M}_{y}{\alpha }_{1}{\alpha }_{2}-2{e}_{x}{e}_{y}{M}_{x}{M}_{y}{\alpha }_{1}{\alpha }_{2}+{e}_{x}^{2}{M}_{x}^{2}{\alpha }_{2}^{2}\right],$$

$$\text{MSE}\left({M}_{\text{y}}^{*}\right)={M}_{y}^{2}-2{M}_{y}^{2}{\alpha }_{1}-\frac{7}{4}\varphi \times {C}_{x}^{2}\times {M}_{y}^{2}{\alpha }_{1}+\varphi \times {R}_{\text{yx}}{C}_{y}{C}_{x}{M}_{y}^{2}{\alpha }_{1}+{M}_{y}^{2}{\alpha }_{1}^{2}+2\varphi \times {C}_{x}^{2}{M}_{y}^{2}{\alpha }_{1}^{2}-2\varphi \times {R}_{\text{yx}}{C}_{y}{C}_{x}{M}_{y}^{2}{\alpha }_{1}^{2}+\varphi \times {C}_{y}^{2}{M}_{y}^{2}{\alpha }_{1}^{2}-\varphi \times {C}_{x}^{2}{M}_{x}{M}_{y}{\alpha }_{2}+2\varphi \times {C}_{x}^{2}{M}_{x}{M}_{y}{\alpha }_{1}{\alpha }_{2}-2\varphi \times {R}_{\text{yx}}{C}_{y}{C}_{x}{M}_{x}{M}_{y}{\alpha }_{1}{\alpha }_{2}+\varphi \times {C}_{x}^{2}\times {M}_{x}^{2}{\alpha }_{2}^{2},$$

(23)

$${\alpha }_{1opt}=\frac{8+3\varphi {C}_{x}^{2}}{8(1+\varphi {C}_{x}^{2}+{C}_{y}^{2}(\varphi -\varphi {R}_{\text{yx}}^{2}))},$$

$${\alpha }_{2opt}=\frac{{M}_{y}(\varphi {C}_{x}^{3}+8{C}_{y}{R}_{\text{yx}}+3\varphi {C}_{x}^{2}{C}_{y}{R}_{\text{yx}}-4{C}_{x}(1+\varphi {C}_{y}^{2}(-1+{R}_{\text{yx}}^{2})))}{8{C}_{x}{M}_{x}(1+\varphi {C}_{x}^{2}+{C}_{y}^{2}(\varphi -\varphi {R}_{\text{yx}}^{2}))}.$$

Putting the optimum values of ${\alpha }_{1opt}$ and ${\alpha }_{2opt}$ in Eq. (23), we got the minimum mean square, we have:

$$\text{MSE}{({M}_{\text{y}}^{*})}_{\text{min}}={M}_{y}^{2}-\frac{{M}_{y}^{2}\left[64+\varphi {C}_{x}^{2}(64+\varphi \left\{25{C}_{x}^{2}-16{C}_{y}^{2}\left(-1+{R}_{\text{yx}}^{2}\right)\right\}\right]}{64\left[1+\varphi {C}_{x}^{2}+\varphi {C}_{y}^{2}\left\{1-{R}_{\text{yx}}^{2}\right\}\right]}.$$

(24)

Numerical study

In this section, we take three actual data sets to observe the efficiency of an estimators. Here, we consider three actual data sets. The PRE of ${\widehat{M}}_{i}$ with respect to ${\widehat{M}}_{y}$ is carried using below expression.

$${\text{PRE}}=\frac{\text{Var}\left({\widehat{M}}_{y}\right) }{MSE\left({\widehat{M}}_{i}\right)}\times 100.$$

Population 1: [Source²⁸].

Y = Number of faculty, X = Number of students in 4 diverse schools under 36 districts in Punjab.

N = 144, n = 10, $\Lambda$ = 0.02327, ${M}_{y}$ = 2023, ${M}_{x}$ = 64,659, fy $\left({M}_{y}\right)$ = 0.00024, fx $\left({M}_{x}\right)$ = 0.00001, ${\rho }_{yx}$ = 0.86110, $C_{My}$ = 2.05965, $C_{Mx}$ = 1.54658, $C_{Myx}$ = 2.74295.

Population 2: [Source²⁹].

Y = Oil prices in present week in 2017, X = Oil prices in preceding week from 2017.

N = 51, n = 11, $\Lambda$ = 0.01782, ${M}_{y}$ = 25.80, ${M}_{x}$ = 25.60, fy $\left({M}_{y}\right)$ = 0.0728, fx $\left({M}_{x}\right)$ = 0.1080, ${\rho }_{yx}$ = 0.9956, $C_{My}$ = 0.53242, $C_{Mx}$ = 0.36168, $C_{Myx}$ = 0.19172.

Population 3: [Source³].

Y = Advanced degrees in 2007 of US, X = Advanced degrees in 2006 of US.

N = 1134, n = 210, $\Lambda$ = 0.00097, ${M}_{y}$ = 48.55, ${M}_{x}$ = 48.49, fy $\left({M}_{y}\right)$ = 0.0075349, fx $\left({M}_{x}\right)$ = 0.0075437, ${\rho }_{yx}$ = 0.9953, $C_{My}$ = 2.73359, $C_{Mx}$ = 2.7378, $C_{Myx}$ = 7.43791.

Empirical study

In this section, a simulation study was acknowledged to estimate the performance of the estimators empirically. Three populations are generated of size 1500 from normal population with theoretical means 5, for both Y and X. The variance covariance metrics used for three different populations are given by:

Population 1:

$$\sum =\left[\begin{array}{cc}12& 4\\ 4& 3\end{array}\right].$$

Population 2:

$$\sum =\left[\begin{array}{cc}8& 4\\ 4& 2\end{array}\right].$$

Population 3:

$$\sum =\left[\begin{array}{cc}10& 2.9\\ 2.9& 3\end{array}\right].$$

The sample sizes n = 50, 150, 250 are chosen in each population. The population density functions for Y and X are calculated utilizing normal distributions. Tables 3 and 4 comprise the mean square error and percentage relative efficiency based on the simulated data.

Conclusion

In this article, we have suggested an enhanced estimator for estimation of population median under simple random sampling using auxiliary variable. Up to the first order of approximation, we evaluated into the bias and MSE of the suggested estimator. Three different datasets are used to evaluate the proposed generalized class of estimators against existing estimators. To check the novelty of estimator a simulation study is also conducted. The results of mean square error and percentage relative efficiency using actual data sets are given in Tables 1 and 2. Three simulated populations are generated of population size 1500 from normal distribution with theoretical means 5, for both Y and X. The sample sizes n = 50, 150, 250 are chosen in each population. The population density functions for Y and X are calculated utilizing normal distributions. The results based on simulation study include on Tables 3 and 4. Based on outcome of actual data sets and a simulation study, we can observe that the suggested estimator achieved minimum MSE and the higher percentage relative efficiency. This shows that the suggested estimator is more efficient for practical determinations when compared to other estimators. Consequently, regarding the new survey, we highly suggest choosing the suggested estimators discussed in this work for calculating the finite population median under the scenario of simple random sampling. The current work can be easily extended to estimation population mean using predictive approach under stratified and systematic random sampling. Further this work is easily extended to estimate population median under stratified random sampling.

Table 1 MSE result of all estimators considered in this article using real data sets.

Table 2 PRE result of all estimators considered in this article using real data sets.

Table 3 MSE result of all estimators considered in this article using simulated data.

Table 4 PRE result of all estimators considered in this article using simulated data.