Human monkeypox disease prediction using novel modified restricted Boltzmann machine-based equilibrium optimizer

Abstract

While the globe continues to struggle to recover from the devastation brought on by the COVID-19 virus's extensive distribution, the recent worrying rise in human monkeypox outbreaks in several nations raises the possibility of a novel worldwide pandemic. The symptoms of human monkeypox resemble those of chickenpox and traditional measles, with a few subtle variations like the various kinds of skin blisters. A range of deep learning techniques have demonstrated encouraging results in image-oriented tumor cell, Covid-19 diagnosis, and skin disease prediction tasks. Hence, it becomes necessary to perform the prediction of the new monkeypox disease using deep learning techniques. In this paper, an image-oriented human monkeypox disease prediction is performed with the help of novel deep learning methodology. Initially, the data is gathered from the standard benchmark dataset called Monkeypox Skin Lesion Dataset. From the collected data, the pre-processing is accomplished using image resizing and image normalization as well as data augmentation techniques. These pre-processed images undergo the feature extraction that is performed by the Convolutional Block Attention Module (CBAM) approach. The extracted features undergo the final prediction phase using the Modified Restricted Boltzmann Machine (MRBM), where the parameter tuning in RBM is accomplished by the nature inspired optimization algorithm referred to as Equilibrium Optimizer (EO), with the consideration of error minimization as the major objective function. Simulation findings demonstrate that the proposed model performed better than the remaining models at monkeypox prediction. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of RMSE is 75.68%, 70%, 60.87%, and 43.75% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Similarly, the proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to accuracy is 9.22%, 7.75%, 3.77%, and 10.90% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively.

Introduction

The monkeypox virus, as per the World Health Organization (WHO), describes the reason for this uncommon illness^1,2. Being a viral zoonotic illness, it may travel from animals to humans and among humans as well as the environment³. After the COVID-19 pandemic was finished, the monkeypox epidemic became the major talked-about issue worldwide^4,5. As of right now, 72,874 confirmed cases—including 28 fatalities—have been found in 12 different sites⁶. The major common symptoms of monkeypox include headache, fever, pains in the muscles, low energy, back pain, and enlarged lymph nodes. A rash may also develop later^7,8,9.

Quickly and accurately diagnosing this condition is quite challenging for medical practitioners^10,11. Nevertheless, early detection of this disease is essential to halt its spread by following further instructions established by the WHO and the initial line of prevention for monkeypox, which involves separation and isolation from others, among various measures¹².

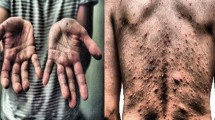
Deep learning is clearly significantly more advanced than traditional machine learning methods such as Random Forest classifier, KNN, and so forth, according to recent study^13,14. They are still computers, though, and they still need human intervention as well as extra subject expertise to handle the classification challenge¹⁵. It is also common for classical machine learning methods to perform well exclusively on the tasks for which they were designed¹⁶. As a result, the conventional machine learning method might not work as well in this domain¹⁵. Recent advances in medical science have been made possible by deep learning methods improved learning abilities, particularly in their variations^{17,18,19,20,21}. Transferring learning methods also aids in addressing the issue of the massive need for datasets. The symptoms of monkeypox disease is displayed in Fig. 1 below.

Figure 1

Visual symptoms of Monkeypox Disease.

The paper contribution is as below.

• To perform an image-oriented human monkeypox disease prediction with the help of novel deep learning methodology.

• To accomplish pre-processing using the image resizing and image normalization as well as data augmentation techniques.

• To undergo the prediction phase using the MRBM, where the parameter tuning in RBM is accomplished by the nature inspired optimization algorithm referred as EO with the consideration of error minimization as the major objective function.

The paper organization is as follows. Section "Introduction" is the introduction of monkeypox disease. Section "Related work" is a literature survey. Section "Proposed methodology" is proposed methodology with proposed model, data collection, pre-processing, feature extraction by CBAM, prediction by MRBM, and EO algorithm. Section "Results" is the results. Section "Discussion" is the discussion. Section "Conclusion" is conclusion.

Motivation

A red lump on the skin is the long-term outcome of a monkeypox infection, which can cause fever, body aches, as well as tiredness in patients. Because of this, people are progressively growing more fearful and nervous, which is commonly reflected in what people think on social media. 28 individuals have died from the virus despite global vaccination campaigns, proving that it is not lethal still is very contagious and can develop into various sub-variants. There could be more cases and fatalities on the globe if they are not appropriately handled and managed. Despite being approved by the FDA, vaccines against the monkeypox virus are currently unavailable and have not been administered to humans. These real-time prediction frameworks could be very useful for healthcare providers and government agencies in directing early responses for the very successful as well as timely control of this disease. They could also be utilized to make decisions about controlling present opportunities.

Related work

On the basis of the M protein amino acid sequence and the MPXV nucleic acid sequence, phylogenetic trees were built in this work²². AlphaFold v2.0 was used to estimate the MPXV_VEROE6 M proteins' 3D format. According to the findings, the MPXV_VEROE6 M protein included 377 amino acids having a somewhat regular spatial arrangement that included a rotating as well as random coil shape. In order to provide theoretical knowledge for the creation of fast diagnostic tools, monoclonal antibodies, and epitope vaccines against the monkeypox virus, this work clarified the evolutionary and structural properties of MPXV membrane proteins.

On the basis of information from the USA CDC, this research employed EpiSIX (an analysis as well as prediction framework for epidemics on the basis of a generic SEIR method) to assess the monkeypox epidemic and anticipate the main trends²³. On May 2, 2022, a global outbreak associated with monkeypox began in the UK, signaling the beginning of an epidemic wave. The striking effectiveness of ring vaccination against monkeypox was demonstrated by simulation findings utilizing EpiSIX. The results validated the need for a 20 day isolation period for close interactions.

The current study's goal was to create a novel mathematical method that investigates the dynamics, future forecast, as well as successful management measures of this newly discovered illness in Nigeria²⁴. Utilizing a typical nonlinear least square minimizing residual approach, the method that fits the real examples the optimal was offered, and the fundamental reproduction count was assessed. Additionally, the method's simulation was used to depict a future state related to the disease, and the dynamics related to the disease was analyzed employing a variety of control methods utilizing actual information. In order to determine the major important framework parameters, a mathematical analysis and a normalized sensitivity analysis of the method was also accomplished in this work. Furthermore, four time-dependent control interventions are used to build an optimum control issue.

Utilizing an ensemble n-sub-epidemic modelling approach on the basis of weekly cases and 10-week calibration intervals, short-term estimates of novel cases of monkeypox was produced across the research regions²⁵. The weekly predictions were presented and evaluated from the second-ranked, ensemble, and top-ranked sub-epidemic methods having quantified uncertainty. Over the previous 10 consecutive prediction periods, the top-ranked method has consistently predicted a declining trend in monkeypox incidence on both country-specific and a global scale. The possible effects of enhanced immunity as well as behavioral change in high-risk groups are reflected in the data.

August 2022 saw the completion of this cross-sectional investigation²⁶. Through the use of educational platforms and social media, an online self-administered questionnaire was used to efficiently gather information from eight Middle Eastern nations. R programme was utilized for doing statistical analysis. There was little public awareness regarding monkeypox in the Middle East. Increasing public knowledge of monkeypox must help the outbreak. The results of this research provide data that might be used to develop health education initiatives.

The purpose of this work was to find putative small interfering RNAs (siRNAs) that may be used to silence E8L and provide a foundation for future therapeutic research²⁷. siRNAs have shown great promise as possibilities for antibacterial, antiviral, and genetic therapy. The study establishes the groundwork for next efforts in genome-level treatments. It may be able to build synthetic RNA molecules that work well as antiviral medications to treat monkeypox virus infections.

The future trajectory associated with the monkeypox outbreak in the United States was forecasted using Facebook's Prophet prediction algorithm, which was made public in 2017²⁸. The 2022 U.S. monkeypox epidemic's range of daily confirmed cases was applicable from May 17, 2022, to August 10, 2022, having a reporting date. The findings indicate monkeypox trends in the United States for durations ranging from seven days to seventeen days. The forecasting accuracy of entire MAPE values in this prediction was good, falling between 0.018 and 0.117. The k-value biasing brought on by unusual occurrences and the use of epidemic control measures may have an impact on the prediction method's accuracy.

In this work, a prediction method was developed for the transmission of the monkeypox epidemic²⁹. For this, specific efficient Neural Network (NN) methods were used. An Artificial Neural Network (ANN) with a single hidden layer was developed and validated using the Levenberg–Marquardt (LM) learning approach.

The goal of this research was to identify the best autoregressive integrated moving average method combinations for capturing the virus's time-dependent flow characteristics and short-term prediction³⁰. The information was compiled from the Our World in Data website and includes information from Brazil, US, France, Spain, Germany, Mexico, Colombia, the UK, Peru, and Canada, among other nations. The autoregressive integrated moving average was a useful tool for short-term prediction and modelling. Various model performance metrics, including RMSE, MAE, and Mean Absolute Prediction Error (MAPE), were presented to support the validity related to the estimated methods.

In this study, images for monkeypox virus prediction were found by utilizing the intrinsic features of PSO, like exploitation and exploration³¹. This research included the following in addition to chickenpox, monkeypox, cowpox, smallpox, tomato flu, measles, and normal skin images for the purpose of predicting as well as diagnosing monkeypox virus. For analysis as well as testing, the images were gathered from the International Skin Imaging Collaboration (ISIC). In order to differentiate monkeypox skin lesions from various skin illnesses, the GLCM-SVM and the classifier hidden Markov method were employed in the diagnostic test. Accuracy, recall, precision, and F1 score are the four performance assessment measures that assess the method as well as examine the results of simulations.

Research gap

The real count of cases of monkeypox infection data represents a collection of findings arranged chronologically. Statistics is where time-series prediction approaches first appeared. For this aim, there are other approaches on the basis of meta-predictors, structure, and machine learning. Numerous academics have worked hard to predict how this illness would spread, including data scientists. Data scientists can make major advances in knowledge by developing prediction methods that highlight the expected characteristics of this virus and enhance the capacity to anticipate its transmission. To the best of knowledge, no substantial research on the monkeypox outbreak has been conducted.

Proposed methodology

Proposed model

The proposed human monkeypox disease prediction model includes various phases such as data collection, pre-processing, feature extraction, and prediction. First, the MSLD standard benchmark dataset is used to collect the data. Using methods for data augmentation, image scaling, and image normalization, pre-processing is carried out using these gathered data. The CBAM technique does the feature extraction on these pre-processed images. The final prediction stage of the MRBM is applied to the retrieved features. The optimization technique known as EO, which is inspired by nature, is used to adjust the RBM's parameters while keeping error minimization as the primary goal. The proposed model’s effectiveness is demonstrated by comparing it with traditional models in terms of distinct analysis like RMSE, MAE, MAPE, MSE, SMAPE, accuracy, precision, recall, and F1 Score. The overall proposed methodology for human monkeypox disease prediction model is depicted in Fig. 2.

Figure 2

Human Monkeypox Disease Prediction model.

Data collection

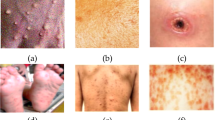
MSLD is utilized to predict cases of monkeypox. There are 228 original images in all in this image collection. The dataset has a 70:10:20 ratio and contains both original as well as enhanced folded images (Train, Test, Validation). For training, the data from the enhanced Train folder is used, which has 2142 images divided into 2 classes (Normal, Monkeypox). Here, the test set only included the original images, but the training as well as validation images from the dataset are enhanced. Medical professionals and researchers investigating the monkeypox virus as well as its effects on human health will find this dataset to be an invaluable resource.

This dataset is made up of several high-resolution images showing different phases as well as cutaneous symptoms of monkeypox infection. An uncommon viral illness called monkeypox resembles smallpox in its signs and develops a rash similar to that of the pox. This collection provides a wealth of images that depict many elements of monkeypox, allowing investigators to examine the disease's course and pinpoint distinctive characteristics that might facilitate a precise diagnosis.

Furthermore, the dataset can be a useful tool for creating as well as testing deep learning methods or computer vision models meant to automatically identify and categorize skin problems linked to monkeypox. Through the use of this information, scientists can learn more about the visual traits of monkeypox and possibly aid in the creation of more effective treatment plans as well as diagnostic instruments. The provision of an extensive and specialized dataset fosters cooperation and makes improvements in the fields of infectious diseases as well as dermatology possible. Some of the sample images attained from the dataset is shown in Fig. 3 below.

Figure 3

Sample images attained from the dataset.

Pre-processing

The pre-processing of the gathered images of the human monkeypox disease prediction model is done by image resizing and image normalization as well as data augmentation techniques. Since preprocessing increases the line for data consistency as well as quality, it is essential to image analysis. The first processing methods used in the work are data augmentation, image scaling, and image normalization.

Image resizing and image normalization The preprocessing techniques from previous trials are presented in this part. For example, image scaling enables researchers to modify the input images to better fit the DL. Even though this approach is carried out prior to the images being input into the methods, it emulates a real-time simulation by conducting the resizing procedure utilizing a fully convolutional layer as portion of the framework. Due to the homogeneity in image size, the images in this research are scaled down to 224 × 224 pixels such that the method could analyze the information more simply. A normalization filter was used to even out variations in the images' contrast and lighting.

Data augmentation To avoid overfitting as well as enhance the dataset, data augmentation approaches are used on images. This increase in the data set increased the accuracy as well as dependability associated with the method. Numerous methods of data augmentation have been put up to overcome these two challenges. The size of the dataset may be gradually increased by regular data augmentation approaches. These methods include, but are not limited to, shearing, rotating (0–360 degrees), flipping, and shifting. With the use of these techniques, which enable the creation of novel images having just little modifications to the original images, a bigger as well as more diverse dataset may be produced. It improve the method's capacity for generalization by augmenting the dataset with vast data. When these strategies are applied, the method is subjected to a greater range of variations, making it more capable of learning the basic features associated with the images. These techniques for growing the dataset enhanced the prediction performance of monkeypox images in terms of both accuracy as well as dependability.

Feature extraction by CBAM

The features are extracted from the pre-processed images of the proposed human monkeypox disease prediction model using the CBAM technique. CBAM is used to extract the most pertinent information from the produced feature maps. Two successive attention-oriented processes are present in CBAM: channel attention and spatial attention. In order to accomplish binary classification, flatten is utilized to convert the layer into a 1D input for the final dense layer, then fed the output into that layer using sigmoid activation. Ultimately, the results from the training information are combined using the validation information.

CBAM describes an adaptive image refining module that focuses more on the key elements associated with the images by applying it in the channel as well as spatial dimensions in a sequential manner. The attention procedure in its simplest form is:

$$ G^{\prime} = N_{d} \left( G \right) \otimes G $$

(1)

$$ G^{\prime\prime} = N_{t} \left( {G^{\prime}} \right) \otimes G^{\prime} $$

(2)

Here, 1D channel attention map ${N}_{d}\in {S}^{D\times 1\times 1}$ and 2D spatial attention map ${N}_{t}\in {S}^{1\times I\times X}$, $G=feature map \left(G\in {S}^{D\times I\times X}=input\right)$, ${G}^{{\prime}{\prime}}$ shows the final refined output, and $\otimes$ stands for element-wise multiplication.

Reducing channel redundancy and focusing on the relationships between characteristics across channels are the main goals of channel attention. The singular spatial descriptors ${G}_{avg}^{d}$ and ${G}_{max}^{d}$ are aggregated using the max-pooling and average-pooling features.

These descriptors are fed into a shared network consisting of a single-hidden-layer Multi-Layer Perceptron (MLP) to produce the channel attention map ${N}_{d}\in {S}^{D\times 1\times 1}$. The output feature vectors are then combined. In general, the computation is:

$${N}_{d}\left(G\right)=\sigma \left(MLP\left(avg\, pool\left(G\right)\right)+MLP\left(\text{max}\,pool\left(G\right)\right)\right)=\sigma \left({X}_{1}\left({X}_{0}\left({G}_{avg}^{d}\right)\right)+{X}_{1}\left({X}_{0}\left({G}_{max}^{d}\right)\right)\right)$$

(3)

Here, ${X}_{0}$, ${X}_{1}$ are the MLP weights, while $\sigma$ is the sigmoid function. After that, the ${N}_{t}\left(G\right)\in {S}^{I\times X}$ spatial attention map is produced using a convolutional layer. To generate a 2D spatial attention map, a traditional convolutional layer concatenates the outcomes related to the pooling operations, ${G}_{avg}^{t}\in {S}^{1\times I\times X}$ and ${G}_{max}^{t}\in {S}^{1\times I\times X}$. The definition of the computations is as below:

$${N}_{t}\left(G\right)=\sigma \left({g}^{7\times 7}\left(\left[avg\, pool\left(G\right);\text{max}\,pool\left(G\right)\right]\right)\right)=\sigma \left({g}^{7\times 7}\left(\left[{G}_{avg}^{t}; {G}_{max}^{t}\right]\right)\right)$$

(4)

In this case, ${g}^{7\times 7}$ = Convolutional operation, $\sigma$ = Sigmoid function, and $7\times 7$ filter size.

Prediction by MRBM

The extracted features of the proposed human monkeypox disease prediction model undergoes the final prediction phase using the developed novel MRBM. Here, the parameters of RBM are tuned by the nature inspired optimization algorithm called EO with the intention of error minimization as the major fitness function. A visible layer $\left(w\right)$ as well as a hidden layer $\left(i\right)$ make up the two layers of the RBM method; the visible layer has $n$ units, while the hidden layer has $o$ units. Any two units among the visible layer as well as hidden layer are linked to each other, but there exists no connection among the internal units of every layer. This is the connection among RBM: the layers are fully connected, and there exists no connection inside the layer. The connection weight within RBM layers is denoted by $x$. $w={\left({w}_{1},{w}_{2},\cdots ,{w}_{n}\right)}^{T}$ stands for the visible layer's state vector, and ${w}_{j}$ for the unit's state. $j$. The hidden layer's state vector is represented by $i={\left({i}_{1},{i}_{2},\cdots ,{i}_{o}\right)}^{T}$, while the ${k}^{th}$ unit's state is represented by ${i}_{k}$. j. The biases vector associated with the visible layer is represented by $b={\left({b}_{1},{b}_{2},\cdots ,{b}_{n}\right)}^{T}$, while the biases related to the unit $j$ are represented by ${b}_{j}$. $c={\left({c}_{1},{c}_{2},\cdots ,{c}_{o}\right)}^{T}$ describes the biases vector associated with the hidden layer and ${c}_{k}$ describes the biases related to the unit $k$.

Every group of variables in an RBM relates to an energy function ${F}_{\theta }\left(w,i\right)$, and the energy function is continuously altered throughout RBM training. RBM describes an energy-oriented method.

$${F}_{\theta }\left(w,i\right)=-\sum_{j=1}^{n}{b}_{j}{w}_{j}-\sum_{k=1}^{o}{c}_{k}{i}_{k}-\sum_{j=1}^{n}\sum_{k=1}^{o}{i}_{k}{x}_{jk}{w}_{j}$$

(5)

The energy function defines the joint probability distribution associated with RBM in the following way:

$$Q\left(w,i|\theta \right)=\frac{1}{A\left(\theta \right)}exp\left(-{F}_{\theta }\left(w,i\right)\right)$$

(6)

Here, $A\left(\theta \right)={\sum }_{w,i}exp\left(-{F}_{\theta }\left(w,i\right)\right)$ describes a normalization factor in the energy function; $n$ and $o$, correspondingly, indicate the count of units in the layer $w$ and $i$; and $\theta =\left\{{x}_{jk}, {b}_{j}, {c}_{k};1\le j\le n, 1\le k\le o\right\}$ represents the RBM parameter.

The following describes the conditional probability distribution associated with the hidden vector $i$ as well as the visible vector $w$:

$$Q\left(w|\theta \right)=\sum_{i}Q\left(w,i|\theta \right)=\frac{exp\left({\sum }_{j=1}^{n}{b}_{j}{w}_{j}\right){\prod }_{k=1}^{o}\left(1+exp\left({\sum }_{j=1}^{n}{x}_{jk}{w}_{j}+{c}_{k}\right)\right)}{A\left(\theta \right)}$$

(7)

$$Q\left(i|\theta \right)=\sum_{w}Q\left(w,i|\theta \right)=\frac{exp\left({\sum }_{k=1}^{o}{c}_{k}{i}_{k}\right){\prod }_{j=1}^{n}\left(1+exp\left(o{\sum }_{k=1}{x}_{jk}{i}_{k}+{b}_{j}\right)\right)}{A\left(\theta \right)}$$

(8)

The conditional likelihood of both visible as well as hidden layer unit activation is as below.

$$Q\left({i}_{k}=1|w\right)=sigmoid\left(\sum_{j=1}^{n}{x}_{jk}{w}_{j}+{c}_{k}\right)$$

(9)

$$Q\left({w}_{j}=1|i\right)=sigmoid\left(\sum_{k=1}^{o}{x}_{jk}{i}_{k}+{b}_{j}\right)$$

(10)

The visible as well as hidden units in the particular RBM framework without any unit-to-unit connections inside the layer are conditionally independent. As a result, the conditional probabilities associated with the hidden vector as well as visible units are displayed as below, accordingly:

$$Q\left(i|w\right)=\prod_{k=1}^{o}Q\left({i}_{k}|w\right)$$

(11)

$$Q\left(w|i\right)=\prod_{j=1}^{n}Q\left({w}_{j}|i\right)$$

(12)

Based on the previously mentioned formulas, RBM describes a network method with an activation function of $sig\left(y\right)=1/\left(1+{e}^{-y}\right)$. The gradient ascent technique is used in the standard RBM training process to maximize the log-likelihood function. Still, the method training is less effective because this technique necessitates a lot of summing operations. Hence, to overcome its limitations, the parameters of RBM are tuned by EO with the intention of error minimization as the main fitness function, thus called MRBM. This MRBM requires fewer summing operations and also overcome the computational complexity problem.

EO algorithm

The EO algorithm is selected here in the proposed human monkeypox disease prediction model for optimizing the parameters of the RBM model in order to derive the error minimization as the major objective function. Models of control volume mass balance that are utilized to describe both dynamic as well as equilibrium states serve as an inspiration for EO. Every particle (solution) in EO functions as a search agent according to its concentration (location). Towards the equilibrium state (ideal outcome), the search agents adjust their concentration at random in relation to the optimal-so-far solutions, or equilibrium candidates. It has been demonstrated that a clearly described "generation rate" term improves EO's capacity for exploitation, exploration, and avoiding local minima.

The physics behind the conservation of exiting, mass entering, and created in a control volume are provided by the mass balance equation. The general mass-balance equation may be expressed as a first-order ordinary differential equation.

$$W\frac{dD}{du}=R{D}_{EQ}-RD+H$$

(13)

The concentration within the control volume $\left(W\right)$ is represented by $D$; the rate of variation of mass within the control volume is $W\frac{dD}{du}$; the volumetric flow rate into as well as out of the control volume is $R$; the concentration at an equilibrium state, where no generation occurs within the control volume, is represented by ${D}_{EQ}$; and the mass generation rate within the control volume is $H$. A condition of stable equilibrium is obtained when $W\frac{dD}{du}$ hits zero. By rearranging Eq. (13), it is possible to get $\frac{dD}{du}$ as a function of $\frac{R}{W}$, in which $\frac{R}{W}$ denotes the turnover rate (i.e., $\lambda =\frac{R}{W}$) or the inverse associated with the residence period, known to as $\lambda$. In order to find the concentration in the control volume $\left(D\right)$ as a function of time $\left(u\right)$, Eq. (13) may therefore also be modified as follows:

$$\frac{dD}{{\lambda D}_{EQ}-\lambda D+\frac{H}{W}}=du$$

(14)

Equation (15) illustrates how Eq. (14) integrates over time:

$${\int }_{{D}_{0}}^{D}\frac{dD}{{\lambda D}_{EQ}-\lambda D+\frac{H}{W}}={\int }_{{u}_{0}}^{u}du$$

(15)

This leads to:

$$D={D}_{EQ}+\left({D}_{0}-{D}_{EQ}\right)G+\frac{H}{\lambda W}\left(1-G\right)$$

(16)

The following describes the calculation of $G$ in Eq. (16):

$$G=exp\left[-\lambda \left(u-{u}_{0}\right)\right]$$

(17)

Here, depending on the integration interval, ${u}_{0}$ and ${D}_{0}$ represent the initial start time as well as concentration. Like the majority of meta-heuristic methods, EO begins the optimisation procedure with the starting population. The following is the construction of the initial concentrations, which are dependent on the count of particles as well as dimensions in the search space and use uniform random initialization:

$${D}_{j}^{initial}={D}_{min}+{Rand}_{j}\left({D}_{max}-{D}_{min}\right) j=\text{1,2},\cdots o$$

(18)

The initial concentration vector associated with the ${j}^{th}$ particle is represented by ${D}_{j}^{initial}$, while the lowest as well as maximum values for the dimensions are shown by ${D}_{min}$ and ${D}_{max}$. ${Rand}_{j}$ describes a random vector within the interval [0,1], and $o$ shows the count of particles in the population. The equilibrium candidates are identified by first sorting the particles based on their objective function evaluation.

The equilibrium state, which aims to be the global optimum, describes the method's final state of convergence. Only equilibrium candidates are chosen at the start of the optimisation procedure in order to offer the particles a search pattern; the equilibrium state is unknown. These candidates are the four optimal-so-far particles found during the whole optimisation procedure plus an additional particle whose concentration describes the arithmetic mean associated with the previously stated four particles. They are dependent on several trials conducted beneath various types of case issues. The average aids in exploitation, but these four alternatives improve EO's capacity for exploration. The count of candidates is determined by the nature related to the optimisation issue and is arbitrary.

$${\overrightarrow{D}}_{EQ,Pool}=\left\{{\overrightarrow{D}}_{EQ\left(1\right)}, {\overrightarrow{D}}_{EQ\left(2\right)},{\overrightarrow{D}}_{EQ\left(3\right)},{\overrightarrow{D}}_{EQ\left(4\right)},{\overrightarrow{D}}_{EQ\left(AVE\right)}\right\}$$

(19)

Every particle updates its concentration in an iteration by selecting a candidate at random from a pool of candidates having an equal probability. For example, the initial particle updates entire concentrations on the basis of ${\overrightarrow{D}}_{EQ\left(1\right)}$ in the initial iteration; it may next update its concentrations on the basis of ${\overrightarrow{D}}_{EQ\left(AVE\right)}$ in the second iteration. Every particle may go through an updating procedure until the optimization procedure is completed, with about equal updates being received by entire potential solutions for every particle.

The exponential term $\left(G\right)$ describes the following term that adds to the primary concentration updating procedure. In order for EO to maintain a sensible balance among exploration as well as exploitation, a precise description of this word is necessary. $\lambda$ is taken to be a random vector in the interval [0,1] as the turnover rate in a real control volume might change with time.

$$\overrightarrow{G}={e}^{-\overrightarrow{\lambda }\left(u-{u}_{0}\right)}$$

(20)

In this case, the count of iterations reduces time, $u$, which is described as a function of iteration $\left(iter\right)$:

$$u=\left(1-\frac{iter}{\text{max}\_iter}\right)\left({b}_{2}\frac{iter}{\text{max}\_iter}\right)$$

(21)

Here, the current as well as maximum count of iterations are represented by $iter$ and $\text{max}\_iter$, correspondingly, and ${b}_{2}$ describes a constant variable that controls the capability to exploit. This additionally considers the following factors to ensure convergence by reducing the search pace and enhancing the method's capacity for exploration as well as exploitation:

$${\overrightarrow{u}}_{0}=\frac{1}{\overrightarrow{\lambda }}ln\left(-{b}_{1}sign\left(\overrightarrow{s}-0.5\right)\left[1-{e}^{-\overrightarrow{\lambda }u}\right]\right)+u$$

(22)

Here, the constant value ${b}_{1}$ governs the capacity for exploration. The stronger the exploration capability and, hence, the lower the exploitation effectiveness, the higher the ${b}_{1}$. In an identical manner, the exploitation capability improves while the exploration capability decreases with increasing ${b}_{2}$. The third factor, $sign\left(s-0.5\right)$, influences the exploration as well as exploitation path. The random vector $s$ ranges from 0 to 1. ${b}_{1}$ and ${b}_{2}$ are equal to 2 and 1, correspondingly, for all of the issues. A selection of test functions is empirically tested in order to choose these constants. On the other hand, these settings may be adjusted as required for various issues. Eq. (23) represents the updated form of Eq. (20) after Eq. (22) was replaced with Eq. (20):

$$\overrightarrow{G}={b}_{1}sign\left(\overrightarrow{s}-0.5\right)\left[{e}^{-\overrightarrow{\lambda }u}-1\right]$$

(23)

One among the key components associated with the suggested method that enhances the exploitation stage and yields the precise answer describes the generation rate. There exist several methods that may be utilized to describe the generation rate as a function of time in a variety of engineering applications. One versatile method, for instance, is described as follows:

$$\overrightarrow{H}={\overrightarrow{H}}_{0}{e}^{-\overrightarrow{l}\left(u-{u}_{0}\right)}$$

(24)

Here, $l$ describes a decay constant and ${H}_{0}$ represents the starting value. This work assumes that $l=\lambda$ and employs the earlier determined exponential term in order to have a more regulated as well as methodical search pattern and to reduce the count of random variables. Consequently, the following represents the final generation rate equations:

$$\overrightarrow{H}={\overrightarrow{H}}_{0}{e}^{-\overrightarrow{\lambda }\left(u-{u}_{0}\right)}={\overrightarrow{H}}_{0}\overrightarrow{G}$$

(25)

$${\overrightarrow{H}}_{0}=\overrightarrow{GCP}\left({\overrightarrow{D}}_{EQ}-\overrightarrow{\lambda }\overrightarrow{D}\right)$$

(26)

$$\overrightarrow{GCP}=\left\{\begin{array}{c}\begin{array}{cc}0.5{s}_{1}& {s}_{2}\ge GP\end{array}\\ \begin{array}{cc}0& {s}_{2}<GP\end{array}\end{array}\right.$$

(27)

Here, the values ${s}_{1}$ and ${s}_{2}$ represent random integers in the interval [0,1], and the GCP vector is created by repeating the value obtained from Eq. (27). The Generation rate Control Parameter, or GCP, is described in this equation as the generation term's potential contribution to the updating procedure. Another term, Generation Probability (GP), determines the likelihood of this contribution. The contribution's procedure is ascertained using Eqs. (26) and (27). Every particle is involved in Eq. (27). For instance, if $GCP = 0$, then $H = 0$, and all of that particular particle's dimensions are updated without the need for a generation rate term. $GP = 0.5$ results in an excellent balance among exploration as well as exploitation. Lastly, the following may be the EO updating rule:

$$\overrightarrow{D}={\overrightarrow{D}}_{EQ}+\left(\overrightarrow{D}-{\overrightarrow{D}}_{EQ}\right)\cdot \overrightarrow{G}+\frac{\overrightarrow{H}}{\overrightarrow{\lambda }W}\left(1-\overrightarrow{G}\right)$$

(28)

Here, $W$ is regarded as the unit and $G$ is specified in Eq. (23). In Eq. (28), the equilibrium concentration is represented by the initial term, and the concentration changes are represented by the second as well as third terms. The task of finding an optimal location in the space is delegated to the second term. Because it makes a greater contribution to the exploration process, this term is able to capitalise on significant concentration changes, or the difference among an equilibrium as well as a sample particle. The third term helps to improve the accuracy of the response since it makes a point. Therefore, this term is more exploitative and gains from concentration fluctuations that are minor and controlled by the generation rate term (Eq. 25). The second as well as third terms may have the identical sign or opposite sign based on factors like the concentrations of equilibrium candidates and particles as well as the turnover rate $\left(\lambda \right)$.

Every particle's fitness value in the present iteration is compared to the one from the earlier iteration, and if a superior match is found, that value will be rewritten. This process helps with exploitation capacity, but if the approach does not benefit from global exploration capability, it may enhance the likelihood of being stuck in local minima. Algorithm 1 presents the pseudo code for the suggested EO algorithm.

Algorithm 1

EO.

Results

Experimental setup

The proposed MRBM-EO model for the proposed human monkeypox disease prediction model was implemented in MATLAB and the findings were analyzed. The operating system used is Windows 10. The CPU used is i5-7300 CPU @ 2.50 GHz and the RAM has a storage capacity of 16 GB. The population size and the iteration count was fixed to 10 and 100. MSLD is utilized to predict cases of monkeypox. There are 228 original images in all in this image collection. The dataset has a 70:10:20 ratio and contains both original as well as enhanced folded images (Train, Test, Validation). The pre-processing for the gathered data is done by image resizing, image normalization, and data augmentation. The parameters of the RBM such as the weight and bias are tuned by EO optimizer with the intention of error minimization as the fitness function. The proposed MRBM-EO model was compared with various methods such as PSO-SVM³¹, Xception-CBAM-Dense³², ShuffleNet³³, and RBM³⁴ in terms of distinct analysis like Root Mean Square Error (RMSE), Mean Absolute Error (MAE), MAPE, Mean Square Error (MSE), Symmetric Mean Absolute Percentage Error (SMAPE), accuracy, precision, recall, and F1 Score to demonstrate the betterment of the developed methodology. The sample output images attained from the proposed MRBM-EO model for the developed human monkeypox disease prediction framework is shown in Fig. 4 below.

Figure 4

Segmented images attained from the proposed MRBM-EO model for the developed human monkeypox disease prediction framework.

RMSE analysis

The RMSE analysis of the proposed MRBM-EO model for the developed human monkeypox disease prediction model and the conventional models is revealed in this section as shown in Table 1 and Fig. 5. It reflects the square root associated with the average squared discrepancies among the goal value as well as the model output value. The RMSE must quit dropping while the count of epochs grows, so that the training stage may be finished. The method that ranks highest has the lowest RMSE value. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of RMSE is 75.68%, 70%, 60.87%, and 43.75% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Hence, it can be concluded that the proposed MRBM-EO model accomplished lower RMSE than the other considered existing methods for the developed human monkeypox disease prediction models respectively.

Table 1 RMSE analysis.

Figure 5

RMSE analysis.

MAE analysis

This section presents the results related to the MAE study of the traditional methods and the suggested MRBM-EO model for the created human monkeypox disease prediction model as given in Table 2 and Fig. 6. It describes a measurement associated with the discrepancies among two observations related to the similar occurrence that are paired. To complete the training phase, the MAE should stop declining as the number of epochs increases. The lowest MAE value is found in the approach that ranks highest. The proposed MRBM-EO for the recommended human monkeypox disease prediction model with respect to MAE is 44%, 42.86%, 33.33%, and 20% advanced than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Therefore, it may be said that, for the produced human monkeypox disease prediction models, the suggested MRBM-EO model achieved lower MAE than the remaining approaches that were taken into consideration.

Table 2 MAE analysis.

Figure 6

MAE analysis.

MAPE analysis

The findings from the MAPE analysis of the conventional techniques as well as the recommended MRBM-EO model for the developed human monkeypox disease prediction model are presented in this section as depicted in Table 3 and Fig. 7. It defines a statistic used to gauge how accurate a forecasting system is in making predictions. The MAPE must cease decreasing as the number of epochs rises in order to finish the training stage. The strategy that scores highest has the lowest MAPE value. The proposed MRBM-EO for the introduced human monkeypox disease prediction model in terms of MAPE is 50%, 40.82%, 30.95%, and 17.14% greater than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Thus, it can be concluded that the proposed MRBM-EO model obtained minimal MAPE than the other techniques that were considered for the created human monkeypox disease prediction methods.

Table 3 MAPE analysis.

Figure 7

MAPE analysis.

MSE analysis

This section presents the results associated with the MSE analysis of the traditional methods together with the suggested MRBM-EO model for the created human monkeypox disease prediction model as revealed in Table 4 and Fig. 8. It calculates the average squared difference among the estimated as well as actual values, or the average associated with the squares of the errors. To complete the training step, the MSE should stop lowering as the count of epochs increases. The MSE value of the highest scoring strategy is the lowest. The proposed MRBM-EO for the developed human monkeypox disease prediction model with respect to MSE is 51.72%, 45.10%, 36.36%, and 24.32% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. In light of this, it may be said that the suggested MRBM-EO model produced a lower MSE than the remaining approaches considered for the development of human monkeypox disease prediction models.

Table 4 MSE analysis.

Figure 8

MSE analysis.

SMAPE analysis

The findings of the SMAPE study related to the conventional techniques are shown in this part together with the recommended MRBM-EO method for the developed human monkeypox disease prediction model as demonstrated in Table 5 and Fig. 9. It describes a metric for accuracy that is dependent on percentage or relative errors. The absolute error divided by the precise value's size describes the relative error. SMAPE includes a lower bound as well as an upper bound, unlike MAPE. The SMAPE must cease decreasing as the number of epochs rises in order to finish the training stage. The top scoring approach has the lowest SMAPE value. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of SMAPE is 54.90%, 47.73%, 37.84%, and 23.33% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Given this, it can be claimed that the proposed MRBM-EO method generated a minimal SMAPE than the other methods considered for creating disease prediction methods for human monkeypox.

Table 5 SMAPE analysis.

Figure 9

SMAPE analysis.

Accuracy analysis

In this section, the results associated with the accuracy investigation pertaining to traditional methodologies are displayed together with the suggested MRBM-EO method for the human monkeypox disease prediction model, as illustrated in Table 6 and Fig. 10. This statistic assesses how frequently a machine learning method forecasts the result accurately. By dividing the total count of guesses by the count of right forecasts, accuracy may be computed. The proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to accuracy is 9.22%, 7.75%, 3.77%, and 10.90% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. In light of this, it can be said that, in comparison to the other approaches taken into consideration for developing disease prediction techniques for human monkeypox, the suggested MRBM-EO method produced a higher accuracy.

Table 6 Accuracy analysis.

Figure 10

Accuracy analysis.

Precision analysis

As Table 7 and Fig. 11 shows, the proposed MRBM-EO approach for the human monkeypox illness prediction model is presented in this part together with the findings from the precision research related to established methodologies. The proportion of values that truly belong to a positive class out of all the values that are projected to belong to that class is what this model performance indicator represents. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of precision is 8.31%, 8.02%, 2.79%, and 11.28% higher than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Given this, it can be concluded that the proposed MRBM-EO method achieved a greater precision when compared to the other methodologies considered for creating disease prediction algorithms for human monkeypox.

Table 7 Precision analysis.

Figure 11

Precision analysis.

Recall analysis

In this section, recall findings pertaining to known approaches are provided with the suggested MRBM-EO strategy for the human monkeypox sickness prediction model, as illustrated in Table 8 and Fig. 12. It gauges the frequency with which a machine learning method properly selects positive examples (true positives) from among all of the dataset's real positive samples. The proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to recall is 8.49%, 9.45%, 2.85%, and 12.87% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. In light of this, it can be said that, in comparison to the other approaches taken into consideration for developing disease prediction algorithms for human monkeypox, the suggested MRBM-EO technique obtained a higher recall.

Table 8 Recall analysis.

Figure 12

Recall analysis.

F1 Score analysis

As shown in Table 9 and Fig. 13, this section presents the recommended MRBM-EO technique for the human monkeypox illness prediction model together with F1 Score findings for known approaches. It describes a measurement of the precision and recall harmonic mean. To improve comprehension of model effectiveness, it combines recall and precision into a single statistic. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of F1 Score is 7.51%, 9.76%, 1.80%, and 13.31% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Given this, it can be concluded that the proposed MRBM-EO strategy received a higher F1 Score when compared to the other methods considered for creating disease prediction algorithms for human monkeypox.

Table 9 F1 Score analysis.

Figure 13

F1-Score analysis.

Discussion

The proposed MRBM-EO model for the monkeypox disease prediction is validated against the state-of-the-art methods in terms of distinct measures such as RMSE, MAE, MAPE, MSE, SMAPE, accuracy, precision, recall, and F1 Score. It can be demonstrated clearly that the error measures such as RMSE, MAE, MAPE, MSE, and SMAPE return minimal error than the traditional methods, thereby revealing the superiority of the proposed monkeypox disease prediction model. On the other hand, the proposed model shows higher outcome than the other methods with accuracy, precision, recall, and F1 Score, thereby proving the betterment of the developed monkeypox disease prediction model. Hence, it can be concluded that the proposed monkeypox disease prediction model is better than the other considered existing methods, respectively.

Interpretation of the findings

The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of RMSE is 75.68%, 70%, 60.87%, and 43.75% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the recommended human monkeypox disease prediction model with respect to MAE is 44%, 42.86%, 33.33%, and 20% advanced than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the introduced human monkeypox disease prediction model in terms of MAPE is 50%, 40.82%, 30.95%, and 17.14% greater than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the developed human monkeypox disease prediction model with respect to MSE is 51.72%, 45.10%, 36.36%, and 24.32% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of SMAPE is 54.90%, 47.73%, 37.84%, and 23.33% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to accuracy is 9.22%, 7.75%, 3.77%, and 10.90% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of precision is 8.31%, 8.02%, 2.79%, and 11.28% higher than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to recall is 8.49%, 9.45%, 2.85%, and 12.87% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of F1 Score is 7.51%, 9.76%, 1.80%, and 13.31% superior to PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively.

Implication

The proposed MRBM-EO model for the monkeypox disease prediction showed minimal error in terms of RMSE, MAE, MAPE, MSE, and SMAPE and higher outcome with measures such as accuracy, precision, recall, and F1 Score. In the future, the proposed model must be compared with hybrid deep learning models in terms of these measures to return minimal error and higher positive outcomes for the monkeypox disease prediction model respectively. By presenting the results and thorough analyses, it is possible to hope to provide future researchers as well as practitioners with insightful knowledge about the work and the possibilities of using explainable AI and transfer learning methods to create secure as well as accurate methods for the diagnosis of monkeypox.

Strength and limitations

This research uses a unique deep learning algorithm to accomplish an image-oriented human monkeypox disease prediction. The results of the simulation show that the suggested method outperformed the other methods in terms of monkeypox prediction. There is insufficient justification given by any of the studies for their better prediction rates. Furthermore, no regularization or generalization techniques have been used, which frequently reduces the overfitting problems with DL-oriented techniques. The extent of the existing literature on this issue is still restricted at this moment owing to the limitation of extensive data. It will be interesting to see how the proposed model does on a huge dataset and in several classes in the near future.

Future work

It is predicted that future models built on this dataset for transfer learning would outperform the current ones. Larger datasets will also be used to train the models that are presented in the paper. Additionally, it is expected that hybrid models will be created and assessed in comparison to the existing models. This model will be used in hospitals and clinics in future research.

Conclusion

This research used a unique deep learning algorithm to accomplish an image-oriented human monkeypox illness prediction. First, the MSLD standard benchmark dataset was used to collect the data. Using methods for data augmentation, image scaling, and image normalization, pre-processing was carried out using these gathered data. The CBAM technique did the feature extraction on these pre-processed images. The final prediction stage of the MRBM was applied to the retrieved features. The optimization technique known as EO, which was inspired by nature, was used to adjust the RBM's parameters while keeping error reduction as the primary goal. The results of the simulation showed that the suggested model performed better at predicting monkeypox than the other models. The proposed MRBM-EO for the suggested human monkeypox disease prediction model in terms of RMSE was 75.68%, 70%, 60.87%, and 43.75% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. Similarly, the proposed MRBM-EO for the suggested human monkeypox disease prediction model with respect to accuracy was 9.22%, 7.75%, 3.77%, and 10.90% better than PSO-SVM, Xception-CBAM-Dense, ShuffleNet, and RBM respectively. In the future, the proposed monkeypox disease prediction model can be performed using hybrid deep learning models being tuned with recent nature inspired optimization algorithms.