Comparative study of Sombor index and its various versions using regression models for top priority polycyclic aromatic hydrocarbons

Abstract

The aromatic compounds having structural configurations with two or more fused benzene rings are the polycyclic aromatic hydrocarbons (PAHs). Topological indices are valuable tools for studying the structure property relationships of PAHs and also helps in predicting various properties and activities. They find applications widely in computational chemistry, drug design and QSPR studies. This article focuses on analysing the potential predictive index for Sombor index (SO), elliptic Sombor index (ESO), Euler Sombor index (EU), reverse Sombor index (RSO), reverse elliptic Sombor index (RESO) and reverse Euler Sombor index (REU) using regression models for top priority 38 PAHs. From the study it is evident that, SO and RSO have proved to be potential predictive indices among the considered degree-based and reverse degree-based indices. The variation of best predictive index with minimal RMSE are plotted for linear, quadratic and cubic regression models for better understanding.

Introduction

A branch of mathematics, that applies the concept of graph theory to study molecular structures is chemical graph theory(CGT). Using CGT, PAHs are modelled into graphs where atoms are represented as vertices and the bond between the atoms are represented as edges. The connectivity of the atoms are analysed with respect to properties of these graphs where researchers gather information about the structure of PAHs molecules^1,2,3,4,5.

In general, CGT equips a dynamic framework for understanding the structure property relationships in PAHs molecule which is necessary for applications in the fields of design of new materials, monitoring environment and pharmaceuticals. A powerful tool to encode the structural information of PAH molecules in numerical representation is obtained by molecular descriptors. These molecular descriptors may be distance-based, graph spectral-based, and degree-based are used in QSPR/QSAR (quantitative structure property/activity relationship) studies to predict the physicochemical properties of PAH compounds^6,7,8,9,10.

A topological index (TI) is the numerical value associated with the molecular structure of a chemical compound. These indices provide an understanding into various physicochemical properties and biological activities of a molecule^{11,12,13,14,15,16,17,18}. Polycyclic aromatic hydrocarbons(PAHs) are composed of multiple aromatic ring having significant applications in the field of pharmacology, materials science and environmental science^19,20,21. In the literature, various TIs are studied to characterize the structural properties of PAHs. They include Wiener index (W) which was the oldest and first TI based on distances between pairs of vertices in a graph. This index contributes information about the molecular size and branching for PAHs.

Hyper-Wiener index (WW) is an extension of the Wiener index which is used in the study of large PAH molecules. The molecular connectivity and symmetry in PAHs are provided using Harary Index (H), since this index is based on average distance between pairs of vertices. The Balaban index (J) gives insights into the degree of molecular branching and symmetry of PAHs as this index is based on topological distance matrix. The information about branching and symmetry of PAHs is obtained by using Randic index (R)^22,23,24,25.

The main axioms of core chemistry postulates that there is an intricate link between the molecular structure with that of its physical properties. Topological indices are worthy in extracting appropriate details of the construction of molecules, thereby proving its applications across diverse fields such as medicinal chemistry, pharmacy, materials science and etc.,^{26,27,28,29,30,31,32,33}.

In 2021, Gutman introduced Sombor index using Euclidean geometry which has become very popular within a short span of time for its contribution in chemistry and pharmacology. The general form of a vertex degree-based index is a function which is chosen such that, it satisfies symmetry property. The edge uv representation in 2-dimensional coordinate system is called the degree-point of the edge uv. The Euclidean distance between the degree-point $(d_u,d_v)$ and the origin O is $\sqrt{d_u^2+d_v^2}$ which is the definition of Sombor index³⁴.

In 2023, Gutman et al., introduced another version of Sombor index called elliptic Sombor index referring to the orbits of planets in the solar system which takes elliptic orbits with the Sun as focus point. In astronomy, the perimeter of an ellipse is of great importance from which elliptic Sombor index was derived³⁵.

In 2024, Gutman et al., showed that, in ellipse, the lengths of semi major and the semi minor axes are equal. The area of the ellipse was found to be $\pi \sqrt{\sqrt{(d_u^2+d_v^2)}(d_u+d_v)}$. Leonard Euler found the approximate perimeter of the ellipse as $\pi \sqrt{2(d_u^2+d_v^2)(d_u+d_v)^2}$. Using these relations, Euler Sombor index was proposed as $\sqrt{d_u^2+d_v^2+d_u.d_v}$. Algebraically, there is a geometric analogy of Sombor and Euler Sombor indices³⁶.

Numerous research work have been carried out on the above indices world wide. The information about graph degree could be relied on the new topological index introduced by Gutman in the year 2021, known as Sombor index. It has been proved that, it holds promise for decoding the thermodynamic behaviour of compounds. Hayat et al.,³⁷ proposed the minimum Sombor index of graphs while Sakandar et al.³⁸ employed valency-based indices in QSPR studies for monocarboxylic acids for physicochemical properties.

In a very short time of its existence, the Sombor index has attracted appreciable attention from both chemists as well as mathematicians. Redžepovi’c³⁹ studied about the alkane’s entropy and enthalpy of vaporization by statistical techniques. The mathematical aspects of Sombor index is studied by Gutman et al.⁴⁰ giving more insights into the topic. The researchers are continuously studying about the Sombor index in which numerous articles are being published for which the extremal values of the index within graphs are considered as the foundation⁴¹.

Using domination numbers for trees, Sun and Du^42,43 studied for the maximal Sombor index. Zhou et al.⁴⁴ used unicyclic graphs and classified the Sombor index with matching number. Li et al.⁴⁵ derived the extreme value of Sombor index for trees with fixed diameter. Réti et al.,⁴⁶ studied about the maximizing graphs for Sombor index using K-cyclic graphs where K takes the values from 1 to 5.

Narahari et al.⁴⁷ introduced a new vertex degree-based index known as reverse Sombor index for which mathematical properties are defined recently. Kulli⁴⁸ established some mathematical properties of reverse elliptic Sombor index for two families of dendrimer nanostars.

Carlos et al.⁴⁹ recently solved the extremal value problem of elliptic Sombor index with equal number of vertices over the set of chemical graphs and chemical trees. Shanmukha et al.⁵⁰ focussed on the chemical applicability of elliptic Sombor index using various benzenoid hydrocarbons through curvilinear regression models.

There has been a momentous progress in the study of the correlation capabilities of several families of graph theoretic descriptors. Gutman and Tosovi’c⁵¹ initiated this study to assess the quality of degree-based indices which was measured by correlation with the physicochemical properties of octane isomers. It was followed by Malik et al.⁵² to continue this study for benzenoid hydrocarbons for the characteristics that included total $\pi$-electronic energy.

Motivated by the above studies on Sombor index and its various versions, an attempt is made to study degree-based indices: Sombor index, elliptic Sombor index, Euler Sombor index and its reverse degree-based indices. To establish the potential index with respect to various physicochemical properties of top priority 38 PAHs using regression models is carried out.

This article mainly concentrates on

• Identifying the potential vertex degree-based topological index in the considered indices with respect to physicochemical properties of top priority 38 PAH’s: Sombor index, elliptic Sombor index, Euler Sombor index and its Reverse degree-based indices.

• To check the potential index, statistical analysis is carried out using regression models.

• We employ RMSE measure to find the minimal error between the set of actual values and the predicted values.

• Based on the obtained RMSE values in this work, we opt for minimal RMSE value which signifies minimal error between the actual and predicted values.

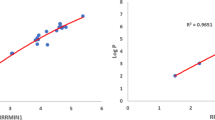
• For better understanding of statistical analysis, a scatter diagram is depicted for linear regression model and is extended for quadratic and cubic regression models with minimal RMSE to notice the variation.

Methodology

G=(V, E) is a simple graph with V as vertex set and E as edge set. For a vertex u belonging to V, $d_u$ indicates the degree of the vertex u^53,54. In this work, the top priority 38 PAHs (Fig. 1) are modeled as molecular graphs for which 6 vertex degree-based topological indices are computed.

Figure 1

Molecular structures of the top priority PAHs.

The considered degree-based indices such as Sombor index, elliptic Sombor index and Euler Sombor index^34,35,36 are defined as follows

$$\begin{gathered} SO(G) = \sum\limits_{{uv \in E(G)}} {\sqrt {d_{u}^{2} + d_{v}^{2} } } \;,ESO(G) = \sum\limits_{{uv \in E(G)}} {(d_{u} + d_{v} )} (\sqrt {d_{u}^{2} + d_{v}^{2} } ) \hfill \\ EU(G) = \sum\limits_{{uv \in E(G)}} {\sqrt {d_{u}^{2} + d_{v}^{2} + d_{u} d_{v} } } . \hfill \\ \end{gathered}$$

Reverse degree-based indices such as reverse Sombor index, reverse elliptic Sombor index^47,48 are defined as follows

$$\begin{gathered} RSO(G) = \sum\limits_{{uv \in E(G)}} {\sqrt {c_{u}^{2} + c_{v}^{2} } } , \hfill \\ RESO(G) = \sum\limits_{{uv \in E(G)}} {(c_{u} + c_{v} )} (\sqrt {c_{u}^{2} + c_{v}^{2} } ). \hfill \\ \end{gathered}$$

An attempt is made to define reverse Euler Sombor index and is defined as

$$REU(G) = \sum\limits_{{uv \in E(G)}} {\sqrt {c_{u}^{2} + c_{v}^{2} + c_{u} c_{v} } } .$$

where $c_u=\Delta -d_u+1$ for any vertex $u \in E(G)$ and $\Delta$ is the maximum vertex degree of the graph G.

Results and discussions

The evaluation of regression models is conducted as follows,

$$y = a + b_{1} x_{1} ;\quad n,\;r,\;F\;(Linear)$$

(1)

$$\begin{aligned}&y=a+b_1x_2+b_2x^2_2;\,\,\,\ n,\,\ r,\,\ F\,\ (Quadratic)\end{aligned}$$

(2)

$$\begin{aligned}&y=a+b_1x_3+b_2x^2_3+b_3x^3_3;\,\,\,\ n,\,\ r,\,\ F\,\ (Cubic) \end{aligned}$$

(3)

Here, y is the dependent variable. a being the regression constant and $b_{i}$ where$(i=1,2,3)$ are the regression coefficients and $x_{i}(i=1,2,3)$ are the independent variables. Samples are used for regression equation, r being the correlation coefficient, SE is the standard error of the estimates and F is the Fisher’s statistic.

RMSE plays a vital role to understand the behaviour of statistical models to evaluate the accuracy of regression models and is used to measure the difference between the actual values and the predicted values. It is defined as

$$RMSE = \sqrt {\frac{{\sum\limits_{{i = 1}}^{n} {(y_{i} - \widehat{{y_{i} }})^{2} } }}{n}}$$

Here, n denotes the number of data points. $y_{i}$ is the actual value for the $i^{th}$ data point, $\hat{y_{i}}$ is the predicted value for the $i^{th}$ data point.

Regression models

In this study, 8 physicochemical properties (Table 1) of PAHs are considered such as molecular weight$(MW \,\ g/mol)$, melting point$(MP\,\ ^{\circ }C)$, boiling point$(BP\,\ ^{\circ } C)$, molar refractivity$(MR \,\ cm^3)$, polarizability $(PO \,\ {10^{-24}}cm^3)$, molar volume$(MV \,\ cm^3)$, flash point$(FP \,\ ^{\circ } C)$, complexity (C) for which coefficient of correlation are calculated using the computed values of TIs (Table 2).

Table 1 Physicochemical properties of top priority 38 PAHs.

Table 2 Computed PAHs values of Sombor index, elliptic Sombor index, Euler Sombor index and its reverse degree-based indices.

From Table 3, it is obvious that of all the 3 degree-based indices considered in the study SO has high correlation with 7 $(MW,\,\ BP,\,\ MR,\,\ PO,\,\ MV,\,\ FP,\,\ C)$ properties out of 8 properties considered while ESO has high correlation with the property MP. From Table 4, it is obvious that of all the 3 reverse degree-based indices considered in the study RSO has high correlation with 7 $(MW, \,\ MP,\,\ BP,\,\ MR,\,\ PO,\,\ FP,\,\ C)$ properties out of 8 properties considered while RESO has high correlation with the property MV.

Table 3 The correlation coefficient r between degree-based TIs and physicochemical properties of PAHs.

Table 4 The correlation coefficient r between reverse degree-based TIs and Physicochemical properties of PAHs.

Linear regression model: Degree-based TIs are studied using linear regression models for Eq. (1), are as follows

$$\begin{gathered} MW = 41.778 + 2.463(SO), \hfill \\ MP = 8.472 + 0.476(ESO), \hfill \\ BP = 178.784 + 3.342(SO), \hfill \\ MR = 19.11 + 0.799(SO), \hfill \\ PO = 7.67 + 0.317(SO), \hfill \\ MV = 7.824 + 1.32(SO), \hfill \\ FP = 36.234 + 2.204(SO), \hfill \\ C = - 26.6 + 4.364(SO). \hfill \\ \end{gathered}$$

Table 5 Various Statistical parameters of linear regression models.

Table 6 Predicted values of physicochemical properties of PAHs from linear regression model with minimal RMSE:$PO=7.67+0.317(SO)$.

Linear regression model

Reverse degree-based TIs are studied using linear regression models for equation (1), are as follows

$$\begin{aligned}&MW=5.061(RSO)-11.62,\\&MP=5.597(RSO)-75.626,\\&BP=7.082(RSO)+95.856,\\&MR=1.683(RSO)-0.184,\\&PO=0.667(RSO)-0.074,\\&MV=0.999(RESO)+23.564,\\&FP=4.703(RSO)-19.988,\\&C=8.522(RSO)-99.813. \end{aligned}$$

Table 7 Various statistical parameters of linear regression model.

Table 8 Predicted values of physicochemical properties of PAHs from linear regression model with minimal RMSE:$PO=0.667(RSO)-0.074$.

Conclusion

This work concentrates on analysing the potential predictive index for SO, ESO, EU, RSO, RESO and REU using regression models for top priority 38 PAHs. From the results, it is evident that Sombor index shows high correlation with considered physical properties compared to that of newly introduced elliptic Sombor and Euler Sombor indices. For best predictive index the minimal RMSE value is considered. From the analysis, it is clear that SO is the best predictive index with minimal RMSE from the considered degree-based indices (Tables 5, 6). RSO is the best predictive index with minimal RMSE from the considered reverse degree-based indices (Tables 7, 8). The variation of best predictive indices with minimal RMSE are plotted for linear, quadratic and cubic regression models for better understanding (Figs. 2, 3). This study may be useful for the researchers who wish to study further about PAHs and also about the applications of the considered indices.

Figure 2

Scatter diagrams of property PO with Sombor index: linear, quadratic, cubic.

Figure 3

Scatter diagrams of property PO with reverse Sombor index: linear, quadratic, cubic.