Introduction

As the Internet of Things (IoT) continues to advance, the construction of smart oilfields places higher demands on the automatic control and fault diagnosis of pumping units. The pumping unit is a vital equipment used for oil well extraction, and the dynamometer card is a key method for analyzing and evaluating the performance of the pumping unit and also plays a crucial role in identifying various downhole conditions.

Conventional methods for acquiring dynamometer cards typically involve installing load sensors at the horsehead of the pumping unit1,2,3. However, due to the harsh environment in oilfield production sites, these load sensors often suffer from damage, distortion, and aging, resulting in large measurement errors and low reliability. Additionally, the long distances between oil wells and the high maintenance costs of load sensors make real-time monitoring of pumping unit operation status challenging.

The electrical parameters of the pumping unit motor are important parameters that can provide real-time feedback on the operating condition of the pumping unit. Recently, several calculation methods have been introduced for switching from motor parameters to dynamometer cards. Li et al. proposed the theory of using the measured power curve of the motor to predict the suspension dynamometer card of the pumping unit4. However, if the inertial force of each moving part and the friction between the bearings are not considered, the result will be a large error. Ma et al. developed a continuous real-time pumping well condition inspection system5, which analyzes oil well condition information by measuring electrical signals, and its basic principle is to apply the torque coefficient method to establish the relationship between electrical parameters and load. Zhang et al. further studied the electric power inversion method of the suspension dynamometer card6, and obtained the correspondence between the motor power and the suspension point displacement. Chen Peiyi used the relationship between ground node force and energy parameters to convert the electrical power into a suspension point dynamometer card7. When calculating the suspension point load torque, it is expressed as a function with Fourier coefficient, the sum of the squares of the errors between the fitting suspension point load torque and the theoretical suspension point load torque is the objective function, and the suspension point load torque is equal to 0 when the power is equal and the torque factor is equal to 0 is taken as the constraint condition, the objective function based on the sum of the square of the suspension point load torque is optimized, and the suspension point dynamometer card is obtained. Zhang et al.8 proposed a method that relies on big data to invert the model of the dynamometer card . Firstly, a sample library of electrical power curves is constructed, and 144 points are selected as key eigenvalues from these electrical power curves. Then, the deep learning technology was used to train these samples, and the conversion model from electrical parameters to dynamometer diagram was successfully constructed. Despite these advances, challenges remain, especially in cases involving specific equipment failures where the quality of dynamometer card is still suboptimal.

With the rapid development of the times, CNN have been widely used in agriculture, industry, and medical fields due to their advantages of automatic feature extraction, the effect of processing spatial transformation, and the reduction of complexity by parameter sharing. However, they also face challenges such as sensitivity to large data volumes and hyperparameters, poor model interpretability, and these factors need to be carefully weighed and optimized in real-world applications to ensure the efficiency and performance of the model. Based on the powerful performance of CNN, this paper proposes an innovative method for inversion of dynamometer card of pumping unit, which combines CNN and electrical parameters to eliminate the interference of pumping unit model and equilibrium state on the inversion of dynamometer card. By combining key parameters such as motor power and crank position, a more efficient and accurate dynamometer card inversion is realized, which provides a new solution for pumping unit performance evaluation. Compared with the traditional method of measuring dynamometer card directly through a force sensor, this method has significant advantages in terms of improved accuracy, reduced cost, and enhanced reliability, but it also faces challenges such as data requirements, implementation complexity, and ongoing maintenance in practical applications.

In summary, the basic experimental procedure of this paper is as follows:By continuously measuring the current, voltage, and power of the motor, one can calculate the output torque and speed of the AC drive motor over time. Integrating the velocity gives the angle of rotation of the crank. Monitoring the change in motor torque, along with the crank’s inclination angle and the geometric parameters of the pumping unit, allows for the calculation of the load \({\varvec{F}}_{{\varvec{t}}}\) and displacement \({\varvec{S}}_{{\varvec{t}}}\) at the suspension point.

The difference between the \({\varvec{F}}_{{\varvec{t}}}\) and actual load is used as the training target, and the voltage, current and crank angle is used as the input variable, and the compensation data is obtained after training by the CNN network, and then the image of the load with displacement of polished rod can be obtained. The flowchart is shown in Fig. 1.

Figure 1
figure 1

Block diagram of the basic experimental flow.

Full size image

Motor speed and torque estimation

In the rod pump oil production system, the motor is the main driving equipment, and it is very important to obtain accurate motor output torque and speed information for calculating the dynamometer card. In this section, we will analyze the working principle of the motor to obtain the relationship between voltage, current, flux, and output torque and rotational speed. The dynamic model of asynchronous motors in a two-phase stationary coordinate system is:

Voltage equation:

$$\begin{aligned} {\left\{ \begin{matrix} u_{\alpha {\text{s}}} = R_{s}i_{\alpha {\text{s}}} + \frac{d\Psi _{\alpha {\text{s}}}}{\text {dt}} \\ u_{\beta {\text{s}}} = R_{s}i_{\beta {\text{s}}} + \frac{d\Psi _{\beta {\text{s}}}}{\text {dt}} \\ u_{\alpha {\text{r}}} = R_{r}i_{\alpha {\text{r}}} + \frac{d\Psi _{\alpha {\text{r}}}}{\text {dt}} + \omega _{r}\Psi _{\beta {\text{r}}} \\ u_{\beta {\text{r}}} = R_{r}i_{\beta {\text{r}}} + \frac{d\Psi _{\beta {\text{r}}}}{\text {dt}} - \omega _{r}\Psi _{\alpha {\text{r}}} \\ \end{matrix} \right. } \end{aligned}$$
(1)

\(u_{\alpha {\text{s}}}\), \(u_{\beta {\text{s}}}\) are stator voltages. \(i_{\alpha {\text{s}}}\), \(i_{\beta {\text{s}}}\) is the stator current, \(R_{s}\), \(R_{r}\) are the stator resistance and rotor resistance, \(\Psi _{\alpha {\text{s}}}\), \(\Psi _{\beta {\text{s}}}\)is the stator flux, \(\Psi _{\alpha {\text{r}}}\), \(\Psi _{\beta {\text{r}}}\)is the rotor flux, \(u_{\alpha {\text{r}}}\), \(u_{\beta {\text{r}}}\)rotor voltage, the value is 0, \(i_{\alpha {\text{r}}}\), \(i_{\beta {\text{r}}}\) is the rotor current, \(\omega _{r}\) is the rotor angular velocity.

Flux linkage equation:

$$\begin{aligned} \left\{ \begin{matrix} \Psi _{\alpha {\text{s}}} = L_{s}i_{\alpha {\text{s}}} + L_{m}i_{\alpha {\text{r}}} \\ \Psi _{\beta {\text{s}}} = L_{s}i_{\beta {\text{s}}} + L_{m}i_{\beta {\text{r}}} \\ \Psi _{\alpha {\text{r}}} = L_{r}i_{\alpha {\text{r}}} + L_{m}i_{\alpha {\text{s}}} \\ \Psi _{\beta {\text{r}}} = L_{r}i_{\beta {\text{r}}} + L_{m}i_{\beta {\text{s}}} \\ \end{matrix} \right. \end{aligned}$$
(2)

\(L_{s}\), \(L_{r}\) and \(L_{m}\) are stator inductance, rotor inductance, and mutual inductance, respectively. In Eq. 3, \(n_{p}\) is the number of pole pairs.

Motor’s output torque T:

$$\begin{aligned} T = \frac{3}{2}n_{p}L_{m}{(i}_{\beta {\text{s}}}i_{\alpha {\text{r}}} - i_{\alpha {\text{s}}}i_{\beta {\text{r}}}) \end{aligned}$$
(3)

In order to obtain motor speed information, we usually use optical sensor to measure the motor speed. However, it is not always advantageous because optical sensor are difficult to install and easily damaged in the field of oil fields. Many methods such as fuzzy sliding mode control, MRAS, observers or time-varying sinusoidal mode extraction (TVSME) method can be used to estimate motor speed. Every of them can be implemented in many ways, and all have some drawbacks9,10,11.

In this paper, a motor speed estimation method based on MRAS algorithm is demonstrated12,13,14,15,16,17,18. The MRAS model consists of a reference model, an adjustable model, and an adaptive structure. The voltage model of the rotor magnetic flux is only related to the voltage and current of the stator, and these electrical parameters can be accurately measured by the electro-energy meter chip. Thus, this model is used as the reference model in this paper. The model is represented by Eq. 4. Where \(\sigma\) is the leakage inductance coefficient and the expression is \(\sigma = 1-L^{2}_{m}/L_{s} L_{r}\).

$$\begin{aligned} \left\{ \begin{matrix} \Psi _{\alpha {\text{r}}} = \frac{L_{r}}{L_{m}}[\int {(u_{\alpha {\text{s}}} - R_{s}i_{\alpha {\text{s}}})dt - \sigma L_{s}i_{\alpha {\text{s}}}}]\\ \Psi _{\beta {\text{r}}} = \frac{L_{r}}{L_{m}}[\int {(u_{\beta {\text{s}}} - R_{s}i_{\beta {\text{s}}})dt - \sigma L_{s}i_{\beta {\text{s}}}}]\\ \end{matrix} \right. \end{aligned}$$
(4)

Because the current model of the rotor magnetic flux includes information about the motor speed, the rotor magnetic flux current model is adopted as an adjustable model. The fluxes computed by this model are marked with a asterisk. The model is represented by Eq. 5. Where \(T_{r}\) is the rotor time constant, and the expression is \(T_{r} = L_{r}/R_{r}\).

$$\begin{aligned} \left\{ \begin{matrix} {\Psi ^{*}}_{\alpha {\text{r}}} = (L_{m}i_{\alpha {\text{s}}} - \omega _{r}T_{r}\Psi _{\beta {\text{r}}})\frac{1}{T_{r}s + 1} \\ {\Psi ^{*}}_{\beta {\text{r}}} = (L_{m}i_{\beta {\text{s}}} + \omega _{r}T_{r}\Psi _{\alpha {\text{r}}})\frac{1}{T_{r}s + 1} \\ \end{matrix} \right. \end{aligned}$$
(5)

This article adopts a PI Control Theory as an adaptive structure, with the difference between the reference model and the output of the adjustable model as the input to the adaptive structure. The purpose of the adaptive structure is to minimize the error between the two models, and a smaller error indicates a closer estimate of the actual motor speed. The deviation is represented by Eq. 6 and the equation for the used adaptive structure by Eq. 7. Where \(K_{p}\) is the proportional gain and \(K_{i}\) is the integral gain.

$$\begin{aligned} e(t)&= \Psi _{\alpha {\text{r}}}^*{\Psi _{\beta {\text{r}}}} - {\Psi _{\alpha {\text{r}}}}\Psi _{\beta {\text{r}}}^* \end{aligned}$$
(6)
$$\begin{aligned} {\omega _r}(t)&= {K_p}e(t) + {K_i}\int _0^t {e(t)dt} \end{aligned}$$
(7)

According to the above analysis, the block diagram of asynchronous motor speed estimation based on MRAS algorithm is shown in Fig. 2.

Figure 2
figure 2

Based on MRAS speed estimation schematic.

Full size image

To validate the performance of the proposed method, this article utilizes the Matlab/Simulink module to construct a simulation model of an asynchronous motor speed and torque estimation system, as shown in Fig. 3. The basic parameters of asynchronous motors are shown in Table 1. The simulation results, as shown in Figs. 4 and 5, indicate that there are some oscillations in the waveform of the speed estimation at the moment of motor startup. However, it quickly tracks the actual motor speed and exhibits good dynamic performance. Oscillation is common during motor start-up. This does not only happen during the start-up phase, but can also occur when the motor is disturbed by changes in external conditions. One of the main causes of oscillation is the initial transient response of the motor. That is, when the motor just starts to run or changes suddenly, it takes a while for the motor to reach a steady state. During this time, the motor’s current, torque, and speed fluctuate.

Figure 3
figure 3

Simulation model for speed and torque estimation.

Full size image
Figure 4
figure 4

Motor speed estimation.

Full size image
Figure 5
figure 5

Motor torque estimation.

Full size image
Table 1 Basic parameters of the motor.
Full size table

Mechanism modeling of beam pumping units

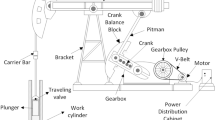
Conventional walking beam pumping units typically consist of a four-bar mechanism (crank, connecting rod, walking beam, and rocker arm). The mechanism drives the crank through the motor to carry out rotary motion(the motor is directly connected to the power grid), and then drives the horsehead to reciprocate up and down through the connecting rod and the traveling beam. By analyzing this mechanism, we can determine the relationship between the suspension point displacement and the crank angle. A simplified schematic diagram of the structure is shown in Fig. 6.

Figure 6
figure 6

Geometric model of pumping unit.

Full size image

Here are the definitions of the mechanical parameters in the diagram:

R: Crank radius (m).

L: Connecting rod length (m).

C: Length of the rear arm of the walking beam (m) .

K: Length of the base pillar, the distance from the support point of the walking beam to the center of the output shaft of the gearbox (m).

A: Length of the front arm of the walking beam (m).

I: Horizontal distance from the support point of the walking beam to the center of the output shaft of the gearbox (m).

H: Height from the support point of the walking beam to the base bottom (m) .

P: Reference line, represents the distance between the center of the crank shaft and the support point of the walking beam (m).

G: The height of the crank shaft to the ground.

Assuming the crank is in the 12 o’clock direction, the position of the polished rod is the zero point of displacement, and the clockwise direction is positive. The polished rod position S* and the torque factor \(\overline{\text {TF}}\) as a function of the crank angle \(\theta\) can be obtained by the sine and cosine theorem19,20,21.

$$\begin{aligned} K&= \sqrt{{H^2} + {I^2}} \end{aligned}$$
(8)
$$\begin{aligned} \alpha&= {\sin ^{ - 1}}\frac{I}{K} \end{aligned}$$
(9)
$$\begin{aligned} \beta&= 2\pi - \theta + \alpha \end{aligned}$$
(10)
$$\begin{aligned} P&= \sqrt{{R^2} + {K^2} - 2RK\cos \beta } \end{aligned}$$
(11)
$$\begin{aligned} \psi&= {\cos ^{ - 1}}\sqrt{\frac{{{C^2} + {P^2} - {L^2}}}{{2CP}}} \end{aligned}$$
(12)
$$\begin{aligned} \lambda&= {\sin ^{ - 1}}(\frac{R}{P}\sin \beta ) \end{aligned}$$
(13)
$$\begin{aligned} \varphi&= \psi + \lambda \end{aligned}$$
(14)

The displacement of the polished rod and crank angle can be expressed by the following equation:

$$\begin{aligned} S^{*}&= A *(\varphi _{\max } - \varphi ) \end{aligned}$$
(15)
$$\begin{aligned} \varphi _{\max }&= \cos ^{- 1}{(\frac{C^{2} + K^{2} - (R^{2} + L^{2})}{2CK})} \end{aligned}$$
(16)

The computing formula of the torque factor is derived as follows, and the simulation results of displacement, velocity, acceleration, and torque factors are shown in Fig. 7.

Figure 7
figure 7

Simulation for movement and torque factor of pump jack.

Full size image
$$\begin{aligned} \overline{TF} = \frac{A}{C}R\frac{{\sin (2\pi - {\alpha _1})}}{{\sin {\beta _{_1}}}} \end{aligned}$$
(17)

When the pumping unit is working, the load at the horsehead is mapped to the torque at the crank through the walking beam and connecting rod, and the torque generated by the crank and counterweight, and the torque output by the motor constitutes a balance of force.

$$\begin{aligned} W = \frac{1}{\overline{\text {TF}}}(T{(\eta _{1}\eta _{2}\eta _{3})}^{i}k + M_{q}) \end{aligned}$$
(18)

Where \(\eta_{1}\) represents the instantaneous efficiency of the motor, \(\eta_{2}\) represents the instantaneous efficiency of the belt, \(\eta_{3}\) represents the instantaneous efficiency of the gearbox, k represents the total transmission ratio of the belt and gearbox, i represents the efficiency index of the pumping unit, and when \(\overline{\text {TF}}\)> 0, i = −1, and when \(\overline{\text {TF}}\) \(\le\) 0, i = 1.

Crank balancing torque \(M_{q}\):

$$\begin{aligned} M_{q} = (W_{a}r_{1} + W_{b}r_{2})\sin {\theta - M_{i}} \end{aligned}$$
(19)

\(W_{a}\) represents the total weight of the crank balance weight, \(W_{b}\) represents the weight of the crank itself. \(r_{1}\) represents the crank balancing radius, which is the distance from the crankshaft to the center of gravity of the balancing block, \(r_{2}\) represents the crank center of gravity radius, which is the distance from the crankshaft to the crank center of gravity. \({M_{i}}\) denotes the torque generated by the inertial load, and the equation is as follows:

$$\begin{aligned} M_{i} = (m_{a}r_{1} + m_{b}r_{2})\frac{d^{2}\theta }{dt^{2}} \end{aligned}$$
(20)

For the asymmetrical structure of the crank balance weight, as shown in Fig. 8, the torque of the balance weight is:

$$\begin{aligned} {W_a}{r_1}\sin \theta&= {W_3}{r_3}\sin (\theta - \alpha ) + {W_4}{r_4}\sin (\theta + \beta ) \end{aligned}$$
(21)
$$\begin{aligned} {M_i}&= ({m_3}{r_3} + {m_4}{r_4} + {m_b}{r_2})\frac{{{d^2}\theta }}{{d{t^2}}} \end{aligned}$$
(22)
Figure 8
figure 8

Asymmetrical structure of the crank balance.

Full size image

Convolutional neural network

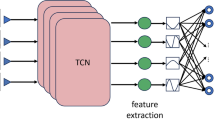
CNN stands for Convolutional Neural Network. It is a deep learning model widely used in the field of computer vision.CNN is inspired by the functioning of the biological visual system. It takes an image’s pixels as input and extracts image features through multiple convolutional and pooling layers. The convolutional layers use a set of filters to perform feature extraction on the input image, and then the pooling layers downsample the extracted features to reduce the number of parameters and computational complexity. Finally, the extracted features are mapped to their respective classes through fully connected layers and output layers22,23,24, its structure as shown in Fig. 9.

  1. 1.

    Convolutional Layers: CNNs have one or more convolutional layers that apply filters (also known as kernels) to the input data. These filters, through the process of convolution, extract spatial features from the input. By sliding the filters across the entire input, different patterns and features are detected.

  2. 2.

    Pooling Layers: CNNs often have pooling layers, which downsample the spatial dimensions of the input data. Common pooling operations include max pooling and average pooling. The pooling layers help reduce the computational burden and abstract the learned features. In practical applications, the effect of max pooling is often better than average pooling, mainly because the maximum feature value in dimension reduction can provide more informative information.

  3. 3.

    Non-linear Activation Functions: Non-linear activation functions, such as ReLU (Rectified Linear Unit), are typically used after each convolutional and fully connected layer in a CNN. These activation functions introduce non-linearities, enabling the network to learn complex patterns.

  4. 4.

    Fully Connected Layers: The fully connected layer acts as a “classifier” in the overall convolutional neural network, mapping the representation of the studied trait to the labeled sample space. In other words, features are collected for final classifier or regression (highly purified characteristics).

  5. 5.

    Training: CNNs are trained using backpropagation with gradient descent. During training, the network learns to optimize its parameters to minimize a specified loss or error function, typically through techniques like stochastic gradient descent (SGD) or more advanced optimization algorithms.

  6. 6.

    Applications: CNNs have achieved state-of-the-art performance in image recognition and classification, it has a wide range of applications, including but not limited to image segmentation, object detection, and speech recognition.

CNN is characterized by parameter sharing and local receptive fields. Parameter sharing means that the filters are shared across the entire image, greatly reducing the number of parameters to be learned. Local receptive fields imply that each filter only focuses on a local receptive field in the input, capturing local features in the image.

Figure 9
figure 9

Structure of CNN.

Full size image

Experimental results

Through the analysis of the kinematics and dynamics mechanism of the pumping unit, as well as the analysis of the asynchronous motor mechanism, a mechanism model based on the reverse calculation of pumping unit electrical parameters for predicting the pumping unit card has been established. Now, we need to collect data from the oil field site for the simulation and analysis of the model.

Figure 10
figure 10

Physical drawing of pumping unit.

Full size image

Taking a typical oil well in the Liaohe Oilfield of China as a case study, the pumping unit model is CYJ10-3-53HB, and its structural parameters and motor physical parameters are shown in the Table 2.

Table 2 Technical parameters of the beam pumping unit.
Full size table

We installed a proximity switch at the 12 o’clock position on the crankshaft base. When the crankshaft rotates to the 12 o’clock position, the proximity switch is triggered, and the electrical parameter acquisition device starts collecting electrical parameter data. When the crankshaft rotates to the 12 o’clock position again, we have collected one cycle of electrical parameter data.We sampled the electrical parameters of more than 10 pumping units, as shown in Fig. 10, and the electrical parameter data of one of the pumping units is shown in Fig. 11. Based on the power graph above, the power of the pumping unit motor varies greatly in one operating cycle.

Figure 11
figure 11

Measured power curve and current curve.

Full size image

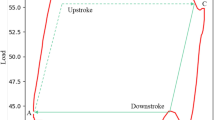
Please simulate the dynamometer card by incorporating the mechanical parameters of the pumpjack and the collected electric motor parameters into the model. Figure 12 shows a comparison between the calculated and actual dynamometer card for one stroke.

According to Fig. 12, it can be observed that there is a significant deviation between the fit dynamometer card generated by the software-based dynamometer card measurement model and the actual dynamometer card. This deviation is particularly pronounced at the top and bottom dead centers, causing the curve to diverge and resulting in poor accuracy of the dynamometer card. This discrepancy is primarily due to the torque factor approaching zero at the dead centers, while the load on the horsehead equal to the torque of the motor and balance block divided by the torque factor. To mitigate this error, this study plans to introduce a CNN (Convolutional Neural Network) to compensate for this deviation.

Figure 12
figure 12

Comparison diagram of indicator diagram.

Full size image

This experiment prepared 2000 sets of data, with 1600 sets of data used as the training set and 400 sets of data used as the test set. The CNN neural network has a convolutional layer with a kernel size of 3*1 and uses the ReLU function as the activation function. The pooling layer uses max pooling, and the RMSE (Root Mean Squared Error) is used as the training evaluation metric. The training and test results are shown in Figs. 13 and 14, respectively.

Figure 13
figure 13

The result predicted by the training set.

Full size image
Figure 14
figure 14

The result predicted by the test set.

Full size image

From Fig. 15, it can be seen that the predicted dynamometer card curve by the CNN neural network after training is very close to the actual curve. To validate the effectiveness of the CNN neural network training, we have selected other neural network models based on the same experimental data, including the Random Forest algorithm (RF), Radial Basis Function (RBF), Particle Swarm Optimization-Backpropagation (PSO-BP) neural network, Extreme Learning Machine (ELM), and Particle Swarm Optimization-Support Vector Machine (PSO-SVM) for comparative experiments. The prediction results are shown in Fig. 16.

Figure 15
figure 15

The prediction result of dynamometer card.

Full size image
Figure 16
figure 16

Comparison of dynamometer card prediction results of different algorithms.

Full size image

Root mean square error (RMSE), mean absolute error (MAE) and Accuracy(the error between the predicted value and the actual value is less than 1 to be accurate) are used as the prediction evaluation indicators. The predicted effect is shown in Fig. 17.

Figure 17
figure 17

Comparison of the prediction effect of each neural network.

Full size image

For pumping units of different structures and pumping units of the same type but with different downhole working conditions, comparative experiments on the prediction effects of various neural networks are also carried out. The prediction results are shown in Figs. 18 and 19.

Figure 18
figure 18

Dynamometer card of pumping unit of different structures.

Full size image
Figure 19
figure 19

Dynamometer card of different working conditions.

Full size image

As shown in Fig. 19a–h, the working conditions of the oil wells are as follows:insufficient liquid supply, sand inflow, travailing valve leakage, standing valve leakage, standing valve lock, gas influence, oil blowout, rod parting.

From Figs. 16, 17, 18 and 19, it can be seen that the predictive performance of the RF and RBF networks is slightly worse, while the PSO-BP and PSO-SVM networks have better prediction results that are closer to the actual dynamometer card curve, but still have small errors in some areas such as top and bottom dead center. In summary, the inversed pumping unit power curve based on the CNN convolutional neural network has a very good performance, and the prediction accuracy as well as the trend changes are very close to the actual dynamometer card curve.

Conclusion

In actual oilfield production processes, real-time and accurate acquisition of pumping unit dynagraph data is of great significance for well fault diagnosis. Due to the limitations of load sensors, this paper proposes a hybrid model for pumping unit dynagraph based on motor electrical parameter data and CNN convolutional neural network, which shows a good agreement with actual data in terms of prediction performance. The advantages of this model can be summarized as follows:

  1. 1.

    Based on the mathematical model of asynchronous AC motors, accurate estimation of the motor’s output torque and real-time speed has been achieved, and verifies the feasibility of this method by building a simulation model using Matlab/Simulink.

  2. 2.

    In order to compensate for data errors, this paper introduces CNN convolutional neural networks and conducts comparative experiments with other neural networks. The experimental results show that the prediction performance of CNN convolutional neural networks is superior.