Introduction

Augmented reality (AR) and virtual reality (VR) are cutting-edge technologies that enable immersive experiences in a rapidly growing number of applications including healthcare1, video-gaming and entertainment2, education3, and manufacturing4. Computer-generated holography (CGH) has emerged as a promising technology for AR and VR displays due to its unique volume image rendering capabilities5,6,7,8,9. With CGH, users can experience a highly immersive environment where virtual objects and scenes are perceived with exceptional realism and accurate depth cues10. Additionally, by rendering true 3D objects to each eye, CGH eliminates the vergence-accommodation conflict, a common issue in AR and VR systems based on 2D near-eye display technology that leads to visual discomfort and eye strain5. CGH also has the advantage of enabling image renderings matched to the morphology of the human visual system, with both wide field capabilities needed to stimulate the peripheral vision, and high-resolution capabilities adjustable to match the human eye’s fovea11. Finally, CGH can be implemented in a compact form factor that is practical for portable and wearable devices8.

The development of CGH-based displays has sparked significant research efforts to enhance physical models8,12 and algorithms for image synthesis6,7,10. To complement these advances, there is currently a growing need for reliable metrics that quantify the realism and immersiveness of display technologies11,13,14. This necessitates the development of advanced Image Quality Assessment (IQA) metrics that align with human perception of image quality. Accurate metrics that can assess the quality of CGH renderings and CGH-specific noise patterns will facilitate the refinement of future CGH algorithms15 and display technologies and enable more immersive and realistic AR and VR experiences.

Multiple IQA metrics have already been developed to evaluate the quality of visual data across a broad range of computer vision applications, including image rendering6,10,13,16,17, image synthesis18,19, transfer20, and reconstruction21,22. There are three categories of IQA metrics, depending on how imaging data is assessed. The first category is Full Reference IQAs (FR-IQA), which compare a target image to a rendered or measured image. The second category is Reduced Reference IQAs (RR-IQA), which quantify image mismatches indirectly by comparing information derived from both the target and the rendered image. The third category is No Reference IQA (NR-IQA), which evaluates a single image for one or more intrinsic properties such as naturalness18,23, sharpness24, or contrast25.

In the context of CGH-based AR and VR displays, FR-IQAs are utilized to quantitatively rate the fidelity of renderings to the target images. Most of the currently available FR-IQA metrics do not incorporate human feedback data to calculate image mismatch scores. Furthermore, these metrics are primarily intended for evaluating images in general computer vision applications, and their sensitivity to distortions that are specific to any particular image-rendering technology is not well understood. For example, images generated using CGH often display ringing patterns, quantization noise, and speckle artifacts that are direct consequences of the wave-like nature of light, or common limitations of the light modulation hardware. The impact of these specific artifacts on human perception of quality, as well as how various FR-IQA methods measure and evaluate them, remains unclear.

Another challenge FR-IQAs face in the context of CGH is that exact matches between target and rendered images are highly unlikely. CGH-rendered images must be feasible solutions to the wave propagation equation, while target images typically do not meet this requirement. As a result, CGH algorithms only aim to identify the best possible approximation. Oppositely, the majority of FR-IQAs are designed to expect exact matches (e.g., mean squared error) or exact correlations (e.g., cosine similarity), and systematically penalize any mismatch, even if they are imperceptible to the human eye. For a precise evaluation of image quality in specialized applications like CGH, FR-IQAs should prioritize penalizing noticeable disparities between target and rendered images while being more tolerant towards mismatches that are less detectable by the human eye.

We developed ConIQA, a new deep learning-based IQA metric, to specifically address these outstanding issues. ConIQA aims to accurately represent human perception and account for domain-specific artifacts with only a limited amount of human-labeled data. We built a Siamese-like network structure and introduced semi-supervised training via consistency training26 to enhance generalization and prevent overfitting. Our model uses both labeled and unlabeled data for loss computation, with the unsupervised loss calculated by measuring the consistency of network predictions. This is achieved by comparing the network predictions before and after random image transformations are applied to both the target and rendering. Since not all image transformations preserve the perceptual quality, we limited our use to horizontal flipping and introduced a new transformation, weighted averaging. We generated a weighted average between the rendering and the target. We assume that it approximates a CGH solution for which the associated perceptual quality is likely an equally weighted average between a hypothetical perfect match and the original perceptual quality. This weighted averaging method can be used in consistency training to enhance generalization.

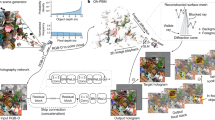
We also created a publicly available labeled dataset (Fig. 1), evaluating the human perception of images rendered with CGH. We selected 1000 high-quality natural images from the KonIQ-10k dataset23 and we generated a CGH rendering for each target image by randomly selecting a CGH algorithm from Gerchberg–Saxton algorithm (GS)27, NOVO-CGH28, and DeepCGH6. We then computed Mean Opinion Score (MOS) values for each pair by asking thirteen human volunteers to rate each pair of images for perceived quality on a scale from 1 to 5 (Fig. 1a), and by averaging these ratings for each pair (Fig. 1b,c,d). The resulting hologram quality assessment dataset, HQA1k, is available on a public repository29. We also assembled a larger unlabeled dataset based on images selected from the KonIQ-10k dataset. We performed image transformations to augment the dataset, then, we paired each image with a rendering from a randomly selected CGH algorithm. The result is an unlabeled dataset of 33,000 target-rendering pairs.

Fig. 1
figure 1

Synthesis and characterization of the HQA1k dataset. (a) Our graphical user interface presented pairs of target-rendering images side by side. Users were asked to rate the quality of images with a score ranging from 1 (poor quality) to 5 (perfect match). (b) We recorded ratings across our entire dataset of 1000 image pairs obtained from thirteen participants. For each target-rendering pair of images, we averaged the 13 ratings to yield a mean opinion score (MOS). The resulting dataset, with 1000 rated image pairs, and associated MOS values is named HQA1k. (c) Histogram of MOS values in the HQA1k dataset. (d) Histogram of per-sample variance of the ratings obtained from thirteen participants evaluating individual image-rendering pairs in the HQA1k dataset.

Full size image

Related prior work

The majority of FR-IQA metrics currently in use are analytical, i.e. they quantify the discrepancies between reference and distorted images through mathematical norms and distances. Key examples of these include Mean Squared Error (MSE)30, Mean Absolute Error (MAE)10,30, Structural Similarity Index Measure (SSIM)31,32, Visual Information Fidelity (VIF)33, and Feature Similarity Index Measure (FSIM)34. Despite MSE and MAE’s ability to measure pixel-level disparities between images, their representation of perceptual quality is not always accurate13. Comparing common FR-IQAs to human perception has shown that SSIM is one of the best analytical FR-IQAs in generic computer vision applications13,35,36. However, none of the advanced analytical metrics, including SSIM, directly incorporate any human-perceived quality data, and the correlations between these metrics and human ratings remain limited13,36 (Fig. 2).

Fig. 2
figure 2

Comparison of ConIQA to existing methods. We used 80% of the HQA1k dataset to train ConIQA. Then we used the remaining 20% to compare ConIQA to other IQA methods on previously unseen data. The radar plot compares the Pearson, Spearman, and Kendall’s tau-b correlation coefficients between ground truth MOS values, and FR-IQA predictions. Higher values indicate a stronger correlation with manually scored image pairs.

Full size image

Advancements in deep learning13,20,37 have made it possible to directly incorporate human-perceived quality data into IQA score computations. Deep learning models are especially adept at handling complex non-linear mappings. Consequently, when these models are trained with IQA datasets scored by humans, they can effectively estimate the perceived quality as experienced by humans13,23,36,38. However, the supervised training of a deep learning FR-IQA model requires a sizable labeled IQA dataset to prevent overfitting22,39. The amount of human input needed for creating such datasets can be prohibitively time-consuming and expensive. A variety of approaches have been explored to tackle this problem and train deep-learning FR-IQA models using smaller IQA datasets20,23,36,38,40,41,42,42,43,44.

The first and most commonly used approach38,41 is “transfer learning”. This technique involves training a neural network on a proxy task, e.g. image recognition. The trained model is used to compute FR-IQA metrics. In these pre-trained models, convolutional layers serve as generic feature extractors that closely resemble human perception of images41,45. Johnson et al.41 introduced “perceptual loss”, where the Euclidean distance between extracted features from the target and distorted image is computed. Zhang et al.38 proposed “Learned Perceptual Image Patch Similarity” (LPIPS). LPIPS further expanded the perceptual loss by calculating the Cosine similarity between these features at all convolutional layers. Both studies showed the benefits of using pre-trained networks for image quality assessment tasks by simply comparing the extracted features. However, since the extracted features are based on an unrelated proxy task, human input is not incorporated directly, and alternative methods must be explored to build human-centric FR-IQA models.

Zhang et al.38 further explored the transfer learning approach by fine-tuning the parameters of the pre-trained neural network. They then used a small fully connected network to predict the final perceptual quality. They also employed data augmentation to prevent overfitting risks associated with the smaller training dataset. This approach has been applied to video quality assessment44 and NR-IQA tasks23, resulting in robust model performance. Despite promising results, feature extractors in these approaches are mainly trained on proxy tasks that are unrelated to IQA, and the final predictions of the network remain imperfect estimations of how humans perceive image quality13,20,37.

The second category of techniques trains an entire network from scratch to take full advantage of the deep neural networks’ nonlinear mapping abilities. However, since available IQA datasets are usually small, additional strategies must be implemented to prevent overfitting. This includes extensive data augmentation techniques38,42,46, reducing the size of the neural networks38,41,46, and/or sharing parameters across Siamese-like38,47 neural network architectures38,41,42,46. For instance, Bosse et al.42 proposed a Siamese-like CNN48 for both FR-IQA and NR-IQA tasks, using publicly available IQA datasets31,49,50 to perform fully supervised training. They augmented the training data, by dividing input images into smaller overlapping patches for individual processing, and the final MOS was obtained from the predictions of each patch. This approach has also been explored in video quality assessment43 by segmenting videos into temporal blocks to further increase the size of the available training dataset.

Despite their promising results, these approaches often rely on image transformations that do not always preserve human-perceived quality in FR-IQA applications. Certain operations like cropping, shearing, and rotation can modify crucial global or local information, affecting perceived image quality. For instance, removing segments with high-frequency patterns via cropping will affect human perception to a greater extent than removing uniform areas devoid of high-frequency content. Moreover, high-frequency speckle might go unnoticed if it overlaps with similar patterns in the target image, and may inadvertently inflate the perceptual quality in that part of the image. Unwanted effects such as the inverted face effect51 or the Thatcher effect52 can occur when applying transformations like rotating or vertically flipping facial images. Shearing can either suppress or magnify image distortions. These specificities of the human visual system limit the validity of patch-based data augmentation techniques42. In high-performance IQAs, global image quality can no longer be deduced from local features within smaller patches. As a result, data augmentation techniques cannot be implemented without first considering their potential impact on FR-IQA scores. Relying solely on these methods during initial neural network training may lead to drift, inaccurate IQA predictions, and ultimately, subpar model performance.

Self-supervised learning53 is appealing for applications such as FR-IQA, where unlabeled data is easy to obtain, but access to labeled data is limited. Recently, Madhusudana et al.40 proposed applying self-supervised contrastive learning for NR-IQA. The principle is to train a network to perform an auxiliary task, which shares similarities with the final task, NR-IQA, but is not equal to the task. After initial training, the pre-trained network operates as a feature extractor for the NR-IQA task, similar to the transfer learning approaches discussed earlier. Even though this approach is more closely aligned with the desired NR-IQA task, the outcomes only showed performance that was either similar or slightly superior to existing methods. Our interpretation of these findings is that it is impossible to achieve a high-performance NR-IQA by exclusively employing unlabeled data to train the convolutional layers (or feature extractors). Also, these results show that defining an auxiliary task that closely corresponds to a NR or a FR-IQA task is challenging. Overall, these results indicate that training CNNs using semi-supervised techniques benefits from utilizing both labeled and unlabeled data.

While significant progress has been made, there are currently no methodologies that effectively utilize unlabeled data without compromising the quality of IQA predictions. Even the best existing self-supervised learning approaches are only marginally better than existing methods. Hence, the next logical step is to devise strategies that maintain high IQA prediction accuracy and leverage both a small amount of labeled data, and a large amount of easily available unlabeled data during training.

Results

We validated our ConIQA model in a FR-IQA task on images generated with Computer Generated Holography. For this, we first trained our model using 80% of the HQA1k dataset and an additional 33,000 unlabeled pairs of target images matched with their CGH renderings. Our model was trained and tested on a RTX 4090 GPU, with a desktop computer operating a Intel Core i9 4900K CPU, with 64GB of Random Access memory. We trained our model through 4000 epochs which required a total time of 45 hours.

We then compared the performances of ConIQA to fifteen other FR-IQA metrics using the remaining 20% of the HQA1k dataset that was not available during training. Inference time for individual frames, after model optimization was 1 millisecond with the same computer and GPU. Batch inference can further reduce this time by at least one order of magnitude. We considered popular and high-performance FR-IQA metrics: LPIPS38, Mean Square Error (MSE)31, Mean Absolute Error (MAE)31, Root Mean Squared Error (RMSE)31, Peak Signal-to-Noise Ratio (PSNR)31, Cosine similarity (Cosine)28, Structural Similarity Index Measure (SSIM)32,54, Multi-Scale SSIM (MS-SSIM)55, Information content Weighted SSIM (IW-SSIM)56, Visual Information Fidelity (VIFp)33, Feature Similarity Index Measure (FSIM)34, Gradient Magnitude Similarity Deviation (GMSD)57, Visual Saliency-induced Index (VSI)58, DCT Subband Similarity Index (DSS)59, and Mean Deviation Similarity Index (MDSI)60.

To compare the performance of these metrics, we first measured the correlation between the ground truth MOS values and the predictions from our ConIQA model on previously unseen data from our HAQ1k dataset. We calculated the same correlations for fifteen other FR-IQAs. Our results (Fig. 2) show that the Pearson, Spearman, and Kendal’s tau correlations are consistently higher with ConIQA (0.98, 0.965, and 0.86, respectively) than with any other FR-IQAs. Correlation coefficients measure the degree of linear relationship between the ground truth MOS and the predictions from various IQA metrics. A higher correlation coefficient with human ratings indicates that the FR-IQA being tested precisely predicts human perception. Our results indicate that ConIQA outperforms all existing metrics.

Imperfect correlations between the scores predicted by an FR-IQA and the ground truth MOS values do not always represent uniform, noise-like, prediction errors across the range of possible scores (0-5). Another possibility is that they represent systemic non-linearities in their predictions. For instance, when comparing the predictions of ConIQA and IW-SSIM (Fig. 3a) we find that although the correlation coefficient between IW-SSIM predictions and ground truth MOS is relatively high, \(r=0.92\), there’s a clear non-linear pattern in the predictions of the model and the overall trend does not follow an ideal identity function. This non-linearity can be indirectly reflected in the slope and intercept of the fitted trend lines. Therefore we fitted similar linear models to all the metrics and we compared the Pearson correlation coefficient to the slope and intercept of the trend lines (Fig. 3b,c). In this context, the correlation coefficient indicates the precision of predictions and the trend line’s slope and intercept indicate the prediction accuracy. For instance, we find that VIFP, Cosine, and PSNR are precise, but not accurate, whereas LPIPS is more accurate but not as precise as ConIQA.

Fig. 3
figure 3

Comparing the slope and intercept of the fitted trend line for predictions by different metrics as a function of ground truth MOS values. The linear trend is defined as \(MOS'=aMOS+b\) where a, and b are slope, and intercept respectively. (a) The scatter plot compares the linearity of predictions by ConIQA and IW-SSIM as a function of ground truth MOS values. (b) Pearson correlation coefficient vs. slope of the fitted lines for all metrics. The dotted black lines represent the ideal values for the correlation coefficient, \(r=1\), and the slope, \(a=1\). (c) Intercept and slope of the fitted trend lines. The dotted black lines represent the ideal values for the correlation coefficient, \(r=1\), and the intercept, \(b=0\).

Full size image

In summary, our results show that ConIQA consistently outperforms other metrics with improved correlation, precision, and accuracy. ConIQA predictions compared to actual human predictions follow a linear trend (Fig. 3a). These results show that ConIQA can reliably infer human perceptions of image quality in the context for which it was trained, with only 800 labeled data points. Since the computation of ConIQA does not depend on the image synthesis technique used to generate the training data, our method can be implemented with any other type of image quality assessment task for which labeled data is difficult to obtain.

Discussion

We have developed and validated ConIQA, a deep learning-based FR-IQA metric that leverages both labeled and unlabeled data for training. ConIQA is specifically designed for image rendering applications where access to labeled image quality assessment data is difficult, expensive, or time-consuming. We employed consistency training to train the model simultaneously with both labeled and unlabeled data. We also introduced an image transformation technique based on weighted averaging for data augmentation in FR-IQA applications.

To validate our approach, and demonstrate ConIQA’s robustness, we considered the case of images rendered with computer-generated holography. For this purpose, we developed a labeled dataset, called HQA1k, consisting of 1000 target and rendering pairs with human-rated quality. ConIQA was trained on 80% of this labeled dataset, and with an additional large unlabeled dataset. Our results indicate that ConIQA consistently outperforms other FR-IQA methods, by reliably predicting MOS values that correlate well with human perception and are accurate, and precise.

Although we validated ConIQA in the context of images rendered with CGH, ConIQA is designed to assess image quality across a broad spectrum of image synthesis, rendering, or manipulation methods and the computation of ConIQA does not set constraints on how the training data is obtained. Our approach is particularly beneficial in contexts where the unique, or experimental nature of the rendering technique makes obtaining large labeled datasets challenging. Thus, the principles of ConIQA extend far beyond the specific application presented in this work, to any other image synthesis technique.

The first and most obvious limitation of our technique is the sample size and the number of human participants who volunteered to manually review our dataset of 1000 image pairs. Recently, crowd-sourcing has enabled the creation of large human-labeled datasets where thousands of humans can collectively rate larger IQA datasets. However, we envision that labeling samples with a smaller number of participants can be sufficient. One way to test this hypothesis would be to train and test ConIQA on a dataset that is labeled by a smaller group of human participants and compare performance with our current results. Beyone CGH applications, further testing of ConIQA in other domains would provide a more comprehensive understanding of the model’s performance, which could be the subject of future studies.

HQA1k and ConIQA evaluations are performed on simulated CGH renderings, which are different from experimentally recorded CGH renderings. While further training and testing on experimentally recorded holograms may help improve our proposed technique, it should be noted that the absence of standardized CGH-based displays introduces challenges to this approach. The imperfections and limitations of the experimental setup that physically renders the hologram to the users will introduce a considerable amount of display-specific distortions to the rendering. This considerably affects the perceptual quality of renderings yet is fundamentally separate from the CGH algorithm and is unique to the display setup being used. However, ConIQA can be trained specifically on experimentally recorded renderings and tan be used to evaluate both the CGH algorithm and the specific display together. For instance, ConIQA can be implemented to evaluate the performance of different CGH algorithms with a particular type of near-eye display hardware.

Future research could also explore extending ConIQA to other applications such as image and video quality assessment, where accurate and reliable FR-IQA metrics are also in demand. For instance, ConIQA could help develop more efficient image and video compression algorithms that prioritize the storage of information that human observers consider important. We expect that the versatility of ConIQA will similarly benefit many other research fields, beyond display technologies and computer vision.

Methods

HQA1k: a labeled dataset for perceptual hologram quality assessment

To validate ConIQA, we considered the use case of Computer-Generated Holography. We developed a labeled dataset, HQA1k, to train, test, and compare ConIQA to other FR-IQA methods. We created HQA1k by first gathering 1000 sample images from the KonIQ-10K dataset23. We specifically selected images that human observers consider to be of high quality according to the KonIQ-10k dataset’s recorded MOS values. This was done to ensure that human evaluations are minimally biased by variations in the inherent quality of the target images. We then randomly selected a CGH algorithm for each image and we calculated a potential CGH rendering. The CGH algorithms we used include Gerchberg–Saxton27, NOVO-CGH28, and DeepCGH6,16. For iterative algorithms, we randomly selected a number of iterations between 10 and 100 to ensure that HQA1k would contain a broad distribution of examples with various levels of mismatches. All samples rated by users exhibited a certain level of correspondence between the target and the rendering, excluding cases where the iterative algorithms diverged.

We displayed each pair of target-rendering in HQA1k on a 1080p display using a custom-designed graphical user interface (see Fig. 1a). Thirteen participants manually reviewed and rated their perception of the degree of the mismatch between the target images and their matched renderings with a grade ranging from 1 to 5. Before scoring image pairs, participants were advised that a grade of ‘1’ signified a poor match while a ‘5’ indicated a perfect match. The image pairs were presented randomly to eliminate bias from previous observations, and to mitigate the effects of experience, and drifts of grading between images that were scored early and late in the sequence. The mean opinion score (MOS) for each sample was calculated by averaging the ratings of all participants (see Fig. 1b). The result is a dataset of 1000 target-rendering pairs matched to a human label representing a suitable FR-IQA score for human perception.

Figure 1c shows the distribution of MOS values across the dataset. We observe that MOS skew toward high values corresponding to high-quality renderings. This uneven distribution is because even a low iteration count can still produce visually accurate solutions. Also, the convergence speed of iterative CGH methods is generally unpredictable and depends both on the type of algorithm and on the target image.

Figure 1d shows the variance of the 13 recorded scores associated with each MOS element in the dataset. Individual perceptions of mismatches between the target and the rendered image do not substantially vary from person to person, indicating that human observers were overall in agreement with each other in their individual perceptions of image quality.

In most Full-Reference Image Quality Assessment (FR-IQA) applications, renderings may be entirely devoid of content. For instance, when initialization effects remain entirely visible after only one iteration of a CGH algorithm. Since our HQA1k dataset does not include these low-quality samples, we incorporated an additional 180 lowest-quality image pairs into the ConIQA’s training set. We paired target images from the KonIQ-10k dataset with renderings made of uniform zeros, uniform ones, or random patterns, that correspond to commonly used initialization values for CGH algorithms, and we assigned to these image pairs a bottom-value MOS score of 0.

ConIQA and consistency training

The notations used in the following sections are listed below along with their descriptions:

\(I_t\):

Target image.

\(I_r\):

Rendered image.

\(\hat{I}_t\):

Transformed target image, for consistency training.

\(\hat{I}_r\):

Transformed rendered image, for consistency training.

M:

Ground truth MOS value associated with the original rendering.

\(M_p\):

Predicted MOS, the output of ConIQA.

\(\hat{M}\):

Expected MOS value after the transformation.

\(\hat{M}_p\):

Predicted MOS, the output of ConIQA for transformed images.

L:

Number of convolutional layers in the Network.

\(H_l\):

Height of the feature maps at Level l.

\(W_l\):

Width of the feature maps at Level l.

\(\textbf{f}_l^t(i,j)\):

Feature vectors at pixel (i, j) in the target image at level l.

\(\textbf{f}_l^d(i,j)\):

Feature vectors at pixel (i, j) in the difference image at level l.

\(\lambda\):

Weight used in transforming the image and MOS value.

ConIQA network structure

Figure 4a shows ConIQA’s network structure. ConIQA is a Siamese-style network where two parallel branches with shared parameters process both the target and the difference image. The difference image is calculated as the absolute value of the difference between the rendered image and the target. Each branch consists of five convolutional blocks, where each block consists of two convolutional layers, each followed by batch normalization. Each convolutional block is followed by a max pooling layer that halves the spatial dimensions of the feature maps. The number of feature maps in the convolutional blocks is doubled after each max-pooling halves the spatial dimensions, a common practice in deep learning model design. Although the parameters of the convolutional layers are shared between the two Siamese branches, the batch normalization layers have distinct parameters to allow for the learning of different statistics in each branch. The final MOS is obtained by calculating the cosine similarity between the extracted feature vectors at each pixel in the target and the difference images, and by averaging their values for all positions across the spatial dimension. While LPIPS includes normalization steps in this process, we chose to omit this for simplicity. The network-estimated MOS, \(M_p\), is obtained by averaging the average cosine similarities at each level, scaled to match the (0-5) range of HQA1k. The output of our ConIQA model, the predicted MOS value, \(M_p\), can be expressed as:

$$\begin{aligned} M_p = \sum _{l=1}^L\frac{5}{L H_l W_l}\sum _{i=1}^{H_l}\sum _{j=1}^{W_l}\frac{\textbf{f}_l^t(i,j)\cdot \textbf{f}_l^d(i,j)}{\left\| \textbf{f}_l^t(i,j)\right\| _2\left\| \textbf{f}_l^d(i,j)\right\| _2} \end{aligned}$$
(1)
Fig. 4
figure 4

ConIQA network structure and the consistency training paradigm. (a) ConIQA is a Siamese-style network where the same network is applied to both the target (top) and the difference (bottom) images. The difference image is defined as \(|I_t-I_r|\). The final estimated perceptual quality, \(M_p\), is calculated by averaging the cosine similarity of feature maps in the two branches. (b) To train ConIQA, we compute a supervised loss, calculated over the HQA1k dataset, as well as an unsupervised loss which is calculated over a large unlabeled dataset of target-rendering pairs. The unsupervised loss is calculated by comparing the network predictions before and after image transformations are applied to each unlabeled sample.

Full size image

Consistency training

Consistency training is a highly advantageous semi-supervised training strategy, especially in scenarios where unlabeled data are abundant. Unlike traditional approaches that heavily rely on labeled data, consistency training leverages both labeled and unlabeled data to calculate both a supervised and an unsupervised loss (Fig. 4b). In our implementation, the supervised loss compares predictions of our ConIQA network to the ground truth labels in HQA1k, using a weighted average (\(\alpha = 0.5\)), of MSE and MAE given by:

$$\begin{aligned} \mathscr {L}_{\text {sup}} = \alpha \text {MSE}(\text {M}, \text {M}_{\text {p}}) + (1-\alpha )\text {MAE}(\text {M}, \text {M}_{\text {p}}) \end{aligned}$$
(2)

To compute the unsupervised loss, we first pass the unlabeled data (\(I_t, I_r\)) through our ConIQA network and record the corresponding Mean Opinion Score (MOS) predictions, \(M_p\) (Fig. 5a). Subsequently, we apply random transformations to the unlabeled data to generate transformed image pairs (\(\hat{I}_t,\hat{I}_r\)) and we record the MOS predictions, \(\hat{M}_p\), of these transformed images from the network. We use the network’s MOS values, \(M_p\), for the original images to independently predict the expected MOS values, \(\hat{M}\), for the transformed images. We performed consistency training using only two image transformations, horizontal flip, and a novel technique called image augmentation by weighted averaging. When only horizontal flipping is applied (Fig. 5b), the expected MOS remains equal to the original MOS, \(\hat{M} = M_p\).

Fig. 5
figure 5

Image transformations used for consistency training in ConIQA. Two types of transformations were used to augment (a) samples from our HQA1k dataset. We considered (b) horizontal flipping, and (c) a novel augmentation method based on weighted averaging. The latter transformation generates a new sample from an existing pair, wherein the target is fixed and the rendering is replaced by a weighted average of the target and the rendering. The weight, \(\lambda\), is a small random number drawn from a uniform distribution in the [0, 0.05] range.

Full size image

The principle for weighted averaging is shown in Fig. 5c. The transformed rendered image, \(\hat{I}_r\), is a weighted average of the target and rendered images given by:

$$\begin{aligned} \hat{I}_r = \lambda \times I_t + (1-\lambda ) \times I_r \end{aligned}$$
(3)

For labeled data, the MOS value of the transformed rendering, \(\hat{M}\), is approximated as the weighted average of the ground truth MOS, M, and 1:

$$\begin{aligned} \hat{M} = \lambda \times 1 + (1-\lambda ) \times M \end{aligned}$$
(4)

For unlabeled data, there is no ground truth MOS value associated with the original rendering. Therefore this will be replaced by the MOS value that the ConIQA predicts for the original pair, \(M_p\). In our experiments, we choose \(\lambda = 0.05\). It is essential to note that during this process, the network isn’t subjected to gradient calculations, instead it serves as an inference tool to estimate the expected MOS for the unlabeled data.

We then equate the anticipated MOS values, \(\hat{M}\), with those generated by the ConIQA network for the transformed images, \(\hat{M}p\). Using a weighted average of MAE and MSE as our loss function, we calculate the unsupervised loss, \(\mathscr {L}_{\text {unsup}}\), given by:

$$\begin{aligned} \mathscr {L}_{\text {unsup}} = \alpha \text {MSE}(\hat{\text {M}}, \hat{\text {M}}_{\text {p}}) + (1-\alpha )\text {MAE}(\hat{\text {M}}, \hat{\text {M}}_{\text {p}}) \end{aligned}$$
(5)

The overall loss is the sum of the supervised and unsupervised losses. With this methodology, our model is capable of learning more robust data representations, which minimizes the risk of overfitting to the labeled data, and improves its generalization potential.

$$\begin{aligned} \mathscr {L} = \mathscr {L}_{\text {sup}} + \mathscr {L}_{\text {unsup}} \end{aligned}$$
(6)