Introduction

Asymmetric optical transmission (AOT) has attracted considerable attention due to its significance in the fields of optical isolators1, cloaking, electromagnetic shielding2,3, and other areas4,5. AOT typically refers to the phenomenon where incident light can only propagate through one side of the structure while being prohibited on the other side. However, in a conventional reciprocal medium, incident light generally exhibits symmetric transmission behavior with respect to incident direction, thereby limiting its utility in various complex systems. To overcome this limitation, a variety of non-reciprocal materials have been applied to electromagnetic transmission systems, such as magneto-optical materials6,7 and nonlinear materials8,9. Many effective AOT schemes have been proposed based on these materials, greatly promoting the development of AOT optical components. However, they also have some non-negligible limitations. For example, magneto-optical materials typically require operation with a magnetic field bias, which hinders their integration into compact systems10. Additionally, nonlinear materials-based AOT devices commonly require high input power and cannot operate when both sides of the structure are excited simultaneously11. Therefore, reciprocal passive AOT devices may be more attractive in the currently desired integrated optical systems.

In recent years, reciprocal micro/nano photonic structures-based AOT devices have been extensively constructed and researched due to their potential application prospects in integrated photonic systems for communication and information processing12,13,14. Although reciprocal AOT devices cannot directly achieve optical isolation, a function typically reserved for non-reciprocal active devices15, they offer some unparalleled advantages, such as a small footprint, high flexibility, and passive operation. Based on the principles of polarization conversion and higher order diffraction, various micro/nano photonic metamaterials that enable the breaking of spatial symmetry have been proposed, such as grating-coupled photonic crystal (PC)16,17, split-ring18,19, asymmetric nanograting20,21, and the like22,23,24,25,26. The asymmetry of these metamaterials selectively transmits incident light with specific polarization states and incidence angles from a single direction, thereby achieving AOT. These research efforts greatly enrich the principle of reciprocal AOT, henceforth promoting the development of reciprocal AOT devices. However, most of these devices only consider a single AOT band and unidirectional transmission in a predefined direction16,17,18,19,20,21,22,23,24,25,26. As optical systems become more complex and integrated, there is a growing demand to introduce versatile reciprocal AOT.

Here, we propose an all-dielectric metamaterial constructed using a nanograting-coupled defective multilayer PC. Based on the coupling of the nanograting-diffracted light with the defect mode and waveguide mode of the PC, the proposed metamaterial can simultaneously achieve multiband and bidirectional multiplexing AOT, that is, significantly different unidirectional transmission bands for different incident directions. Specifically, when illuminated from the defective PC and the nanograting, the metamaterial can achieve a narrowband AOT of ~ 3.9 nm (at 576 nm) and a broadband AOT of ~ 62.7 nm (at 624 nm), respectively. Among them, near-perfect unidirectional transmission at 624 nm can be achieved for transverse magnetic (TM) polarized incident light. Furthermore, the bandwidth, number, and wavelength location of AOT bands can all be flexibly tuned by structural parameters. The proposed metamaterial also exhibits polarization multiplexing characteristics, as the bandwidth and number of AOT bands depend on the polarization angle.

Structural design and AOT mechanism

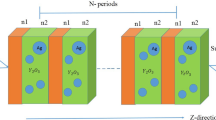
Figures 1a and b depict a three-dimensional schematic and an enlarged cross-section of the proposed AOT metamaterial, respectively. The proposed metamaterial termed the nanograting-coupled multilayer photonic structure, consists of a top TiO2 nanograting, a middle SiO2 dielectric spacer, and a bottom defective multilayer film. Notably, the bottom defective multilayer PC comprises 10 pairs of alternating TiO2 and SiO2 layers of equal thickness, with a relatively thicker SiO2 layer inserted as a defect film. Here, a high refractive index (RI) contrast between the SiO2 and TiO2 layers is chosen to generate a wide range of bandgap, and the defective film is introduced to break the perfect periodicity of the PC and, thus, excite the defect mode. The light illuminating from the dielectric nanograting (defective multilayer PC) to the defective multilayer PC (nanograting) is defined as forward incidence (backward incidence). When illuminated from different directions of the metamaterial, the wavelength and bandwidth of the output beam vary significantly. In this paper, the combination of the finite-difference time-domain (FDTD) simulation, transmission matrix method (TMM)27, and rigorous coupled wave analysis (RCWA)28 are exploited to characterize the optical spectral characteristics and illustrate the working principle of the proposed AOT metamaterial. In the FDTD simulation, the perfectly matched layer along the z-axis and periodic boundary conditions along the x-axis are applied. In Fig. 1b, the structural parameters of the metamaterial are explicitly marked. The thickness of the SiO2 spacer film (h3) between the top nanograting and the bottom defective multilayer, as well as the thickness (h) and width (w) of the nanograting, are fixed as 190 nm, 290 nm, and 300 nm, respectively. The period of nanograting and the thickness of the middle defect layer are marked as P and h1 + hD, respectively, where P and hD are preset to 678 nm and 80 nm, respectively. The thicknesses of SiO2 and TiO2 layers within the bottom PC are denoted by h1 and h2, respectively. They satisfy a quarter-wavelength optical thickness, namely, nihi = λBragg/4 (i = 1, 2), where ni and hi represent the RI and thickness of SiO2 and TiO2 layers, respectively, and λBragg represents the Bragg wavelength. The RIs of the SiO2 and TiO2 layers are fixed at 1.46 and 2.3, and their thicknesses are set to 103 nm and 65 nm for the Bragg wavelength of 600 nm.

Fig. 1
figure 1

The metamaterial composed of nanograting-coupled defective multilayer photonic crystal for multiband and bidirectional multiplexing AOT. (a) Three-dimensional schematic diagram and (b) the enlarged cross-section with geometric parameters. (c) The transmission spectra of the proposed AOT metamaterial illuminated from nanograting to defective PC (red-filled region) and from the defective PC to the nanograting (yellow-filled region). (d) The transmittance difference and contrast ratio of AOT metamaterial at specified peak wavelengths in three different transmission bands. The colors of the bar chart correspond to three peak wavelengths (518 nm: green region, 576 nm: yellow region, 624 nm: red region).

Full size image

Figure 1c demonstrates the transmission spectra of the proposed bidirectional multiplexing AOT metamaterial illuminated with a TM plane wave for two different incident directions. For forward incidence, there is a broadband transmission peak (marked as λ3) at 624 nm with a linewidth of ~ 62.7 nm and a narrowband transmission peak at 518 nm (marked as λ1). However, for backward incidence, there is only a narrowband transmission peak at 576 nm with a linewidth of ~ 3.9 nm (marked as λ2). Since these three bands do not overlap, different unidirectional transmission bands can be realized for two different incident directions, which here is termed bidirectional multiplexing. To quantitatively evaluate the AOT performance of the proposed metamaterial, two factors are considered: transmittance difference (Tport1 − Tport2) and contrast ratio ((Tport1 − Tport2) / (Tport1 + Tport2)) for both directions. As shown in Fig. 1d, the absolute value of transmittance difference and contrast ratio of peak wavelengths in the three bands exceed 0.61 and 0.89, respectively, where the symbol “ − ” in front of the number represents the unidirectional transmission for backward incidence. Notably, the transmittance difference and contrast ratio of the metamaterial for incident light with a wavelength of 624 nm (λ3) is 0.974 and 0.997 (Tport1 / Tport2 = 673), respectively, achieving near-perfect unidirectional transmission. These results prove that the designed metamaterial demonstrates excellent multiband and bi-directional multiplexing AOT.

To elucidate the physical mechanisms of AOT in the metamaterial, we calculate the energy band diagram of the defective PC using TMM, as shown in Fig. 2a. As a direct comparison, the counterpart result of the flawless PC without a defect is depicted in Fig. 2b. When the transverse wavevector (kx) of the incident light is 0, there is a wide bandgap ranging from 520 to 700 nm for the flawless PC. However, the presence of the defective layer within the PC results in a narrow transmission band at λ2. Therefore, the transmission peak λ2 for backward incidence originates from the excitation of the defect mode in the PC. Additionally, with the increase of transverse wavevector kx, the PC defect mode will gradually blueshift to meet the phase-matching conditions. Meanwhile, the inherent transmission band of the PC gradually appears in the energy band diagram and also demonstrates a blue-shift trend. Therefore, the key to unidirectional optical transmission for specific wavelengths is to simultaneously achieve a large difference in transverse wavevector kx at both sides of the PC. In the proposed metamaterial, the diffraction of the top nanograting exactly provides a wavevector compensation for the normally incident light from the nanograting side, resulting in a high kx. The black dashed lines in Fig. 2a and b represent the position of the first-order diffracted light (G = 2π/P) of the nanograting. Since the first-order diffracted light matches the transmission band (λ3) and defect mode (λ1) of the PC, broadband and narrowband transmission are achieved simultaneously for the forward incidence. Notably, the linewidth of the broadband transmission band is equal to the difference between Wood’s anomaly wavelength (kx/k0 = 1) and the wavelength of the diffracted light that coincides with the bandgap boundary. Besides, the defect mode of narrow-band transmission (λ1) is misaligned with the case of kx = 0 (λ2) due to its blueshift with the increase of wavevector, thus realizing a narrowband AOT. For backward incidence, the wavevector of the normally incident light from the backward direction cannot be compensated due to the absence of nanograting, resulting in a narrowband transmission peak at λ2.

Fig. 2
figure 2

The generation mechanisms of multiband and bidirectional multiplexing AOT. TMM-calculated energy band diagrams of one-dimensional (a) defective and (b) flawless photonic crystals for TM-polarized incident light. The black dashed lines represent the transverse wavevector provided by the first-order diffraction of nanograting. (c–e) Amplitude of the x-component of the electric field for the metamaterial illuminated with TM-polarized plane waves at λ = 518, 576, and 624 nm for forward incidence (top panel) and backward incidence (bottom panel).

Full size image

Additionally, the generation mechanisms of transmission peaks λ1, λ2, and λ3 are further analyzed by the spatial distributions of the electric field. Figures 2c–e illustrate the amplitude of the x-component (Ex) of the electric field at wavelengths λ1, λ2, and λ3 for the metamaterial when illuminated by TM-polarized plane waves. The top panels show the results for forward incidence, while the bottom panels show the results for backward incidence. The interior of the defect layer exhibits electric field enhancement at the narrowband transmission peak λ1 for the forward incidence. This is consistent with the typical characteristics of the defect mode, where constructive interference occurs within the defect layer. Moreover, Ex exhibits alternating positive and negative arrangements after the incident light has passed through the nanograting, which proves that the defect mode λ1 is excited by the first-order diffracted light of the nanograting. Similar to transmission peak λ1, the enhanced electric field can also be observed in the defect layer at λ2 for the backward incidence. The difference between them is its relatively uniform Ex distribution along the transverse direction. This indicates that the mode is mainly excited by the normal incident light, not diffracted light with an oblique angle. The faint transmission of the forward incidence is due to the zero-order diffracted light of the nanograting exciting the PC defect mode. Different from the two short-wavelength modes, there is no electric field enhancement in the defect layer at λ3 for the forward incidence. Additionally, Ex exhibits an alternating positive and negative periodic arrangement in both the x and z directions within the defective PC, with relatively uniform intensity, characteristic of a waveguide mode distribution. Therefore, the long-wavelength wideband transmission results from the resonance coupling between the nanograting diffracted light and the waveguide mode in the whole multilayer film, and the defect layer has a weak effect on the excitation of this transmission mode. This is the essence of grating diffracted light matching the transmission band of the dielectric multilayer film.

In addition to its near-field characteristics, the far-field transmission characteristics of the proposed metamaterial are also investigated in detail. Figures 3a–f demonstrate the normalized far-field transmission power distributions at three characteristic wavelengths. For the forward incidence, the normally incident lights at λ1 and λ3 mainly pass through the metamaterial at the first-order diffracted angle (θ = arcsin(G/k0)) of the nanograting. The faint transmission of the normally incident light at λ2 is proved to originate from zero-order diffraction of the nanograting. For the backward incidence, the nanograting serves as the output side of the structure, and the transmitted intensity of the diffracted light remains unchanged since it does not pass through the defective PC. Hence, the proportion of first-order diffracted light in the transmitted light is positively correlated with the first-order diffraction efficiency of the nanograting. As shown in Figs. 3d–f, the first-order diffraction efficiency of the nanograting consistently dominates, with the highest proportion at λ3 and the lowest percentage at λ1. Since the AOT performance of the forward incidence is positively correlated with the first-order diffraction efficiency, the forward transmittance of the metamaterial is lower at λ1 and higher at λ3.

Fig. 3
figure 3

Analysis of the diffraction angle and efficiency of the metamaterial. Normalized far-field intensity as a function of the transmission angle for the metamaterial illuminated with the normally incident TM-polarized light at λ = 518, 576, and 624 nm for (a–c) forward incidence and (d–f) backward incidence. The black dashed lines indicate the position of the first-order diffraction angles, calculated by the relationship of θ = arcsin(G/k0). The insets in the bottom right depict the transmission behavior of light in the metamaterial for three characteristic wavelengths.

Full size image

Flexible adjustable AOT and theoretical calculation

To achieve the multiband and bidirectional multiplexing AOT effectively, a synergistic interplay among the Bragg wavelength of the PC, the thickness of the middle defect layer, and the nanograting period is essential. Figures 4a–c demonstrate the dependence of the transmittance of the proposed AOT metamaterial on three different structural parameters for the forward incidence. With an increase in these three structural parameters, the resonance wavelength of the PC defect mode red shifts progressively. Besides, the linewidth of the broadband transmission peak is negatively correlated with both the Bragg wavelength and the thickness of the defect layer, while its bandwidth shows the opposite trend with the nanograting period. As the nanograting period decreases, the linewidth of the broadband transmission peak gradually decreases, eventually disappearing and transforming into a new narrowband mode when the nanograting period approaches 570 nm. The newly generated narrowband transmission mode originates from the Fabry–Perot resonance occurring in the groove of the nanograting. Additionally, the corresponding results of the backward incidence are shown in Figs. 4d–f, the wavelength position of the narrowband transmission peak caused by PC defect mode exhibits a positive correlation with both the Bragg wavelength and the thickness of the defect layer. When the thickness of the defect layer is greater than 140 nm, a new short-wavelength narrowband transmission peak emerges in Fig. 4e, originating from the excitation of higher-order PC defect mode. Additionally, although the wavelength position of this defect mode is independent of the nanograting period, its transmitted intensity will decrease significantly when the nanograting period is close to its wavelength. This is because when the nanograting period is smaller than the wavelength of defect mode, the first-order diffracted light with kx greater than k0 is completely reflected. To explain the wavelength variation trend of defect mode, its resonance wavelength is quantitatively described by theoretical calculation. In the proposed metamaterial, the excited PC defect mode meets the below phase matching condition:

$$\varphi_{{{\text{PhC1}}}} + \varphi_{{{\text{PhC2}}}} + \varphi_{{{\text{prop}}}} = m2\pi$$
(1)

where φPhC1 and φPhC2 are the reflected phase shifts of the PCs on both sides of the defect layer, and satisfy the following relationship:

$$\varphi_{{{\text{PhC1}}}} { = }\varphi_{{{\text{PhC2}}}} {\text{ = arg(}}r_{{{\text{PhC}}}} {)}$$
(2)

where rPhC is the reflection coefficient of the PCs, which can be obtained by the TMM29:

$$r_{{{\text{PhC}}}} {\text{ = exp}}\left( {i\beta \frac{{\omega - \omega_{{{\text{Bragg}}}} }}{{\omega_{{{\text{Bragg}}}} }}} \right)$$
(3)

where β = πn1/|n1 − n2|, ω = 2πc/λ and ωBragg = 2πc/λBragg are angular frequency of incident light and Bragg frequency, respectively. Besides, the propagation phase in the defect layer φprop can be calculated by the below equation:

$$\varphi_{{{\text{prop}}}} = \frac{{n_{1} 4\pi \left( {h_{1} + h_{D} } \right)\cos \theta_{1} }}{\lambda }$$
(4)

where θ1 is the propagation angle of incident light in the defect layer, and equal to 0 for backward incidence. By combining Eqs. 1–3 and considering m = 1, the relationship between the resonance wavelength of the PC defect mode and both the Bragg wavelength and the thickness of the defect layer can be expressed as follows:

$$\lambda_{{{\text{Bragg}}}} \left( {\lambda_{D} } \right){ = }\frac{{{2}\lambda_{D} \left( {\beta { + }\pi } \right) - 4\pi n_{1} h_{D} }}{2\beta + \pi }$$
(5)
$$h_{D} \left( {\lambda_{D} } \right){ = }\frac{{{2}\lambda_{D} \left( {\beta { + }\pi } \right) - 2\beta \lambda_{{{\text{Bragg}}}} - 4\pi n_{1} h_{{1}} }}{{4\pi n_{1} }}$$
(6)
Fig. 4
figure 4

Dependence of transmission spectra of the designed metamaterial on three structural parameters. The transmittance of the proposed AOT metamaterial illuminated with TM-polarized light as a function of (a) Bragg wavelength, (b) the thickness of the defect layer, and (c) the period of nanograting for forward incidence. (d)-(f) The corresponding results of the backward incidence. In (a–f), the red dashed lines correspond to the wavelength positions of PC defect mode, calculated using Eqs. 5 and 6. The dependence of calculated energy band diagrams of the defective multilayer PC on (g) Bragg wavelength, (h) the thickness of the defect layer, and (i) the period of nanograting. The curves of different colors represent the bandgap edges of the PC with different structural parameters. The dashed lines of different colors represent the transverse wavevector provided by the first-order diffraction of nanograting. The length of the double-arrow line represents the bandwidth of the transmission peak.

Full size image

The functional curves calculated by Eqs. 5 and 6 are plotted in Figs. 4a–f as the red dashed lines, which are in excellent agreement with the FDTD simulation results. For the forward incidence, due to the diffraction effect of nanograting, the propagation angle θ1 in the defect layer is not 0 and is positively correlated with the diffraction angle α of nanograting. According to the nanograting diffraction equation: n1Psinα = λ, the increase in the nanograting period will lead to the decrease of the diffraction angle α and the propagation angle θ1, thereby increasing the propagation phase shift φprop. Therefore, to satisfy the phase-matching condition, the wavelength of the incident light is redshifted accordingly to reduce the propagation phase shift φprop, which is consistent with the simulated results in Fig. 4c.

Moreover, we further analyze the variation trend of the bandwidth of the transmission peak λ3 through the energy band diagrams. As shown in Fig. 4g, an increase in the Bragg wavelength causes a redshift of the photonic bandgap (curves of different colors), thus leading to a redshift in the wavelength position (filled dots with different colors) of the diffracted light coinciding with the bandgap boundary. As above mentioned, the cut-off wavelength and initial wavelength of wideband transmission are determined by the position of Wood’s anomaly wavelength and the wavelength of diffracted light coinciding with the bandgap boundary, respectively. In the case where the Wood’s anomaly wavelength remains constant, the bandwidth of the transmission peak λ3 decreases as the Bragg wavelength increases. Figure 4h shows that the increase in the thickness of the defect layer will also lead to a slight redshift of the bandgap, accompanied by a decrease in the transmission bandwidth. In contrast to the previous two cases, altering the wavelength of diffracted light simultaneously affects both Wood’s anomaly and the other bandgap boundary wavelengths. As shown in Fig. 4i, with the increase of the nanograting period, the positions of both boundaries exhibit a redshift, but the amount of redshift of the Wood’s anomaly wavelength is greater than that of the bandgap boundary. Therefore, the increase of the nanograting period will increase the bandwidth of the transmission peak λ3. When the nanograting period is less than 573 nm, the wavelength of diffracted light falls completely below the bandgap, with no diffracted light matching the transmission band of the PC. As a result, it can barely pass through the metamaterial.

As a comparison, RCWA and TMM methods are also employed to demonstrate the reliability of the simulated results, where TMM only considers the first-order diffraction effect of the nanograting. As shown in Fig. 5a, as the Bragg wavelength increases from 500 to 700 nm, the number of AOT bands of the metamaterial gradually increases from 2 to 5, demonstrating the proposed metamaterial possesses the potential to achieve multiband AOT. Additionally, there are always unidirectional transmission bands in the spectrum for both forward and backward incidence within the investigated parameter range, allowing the metamaterial to achieve bidirectional multiplexing. Figure 5b demonstrates that with the increase of defect layer thickness, the wavelength of narrowband AOT is redshifted, while the transmittance difference approaches 0 when it coincides with the wide transmission band. In this case, a narrowband symmetric transmission appears in the broadband AOT, which may play a role in specific scenarios. Finally, the transmittance difference of the designed structure as a function of the nanograting period is calculated and shown in Fig. 5c. Similar to Fig. 4c, the bandwidth of the AOT band gradually decreases and approaches 0 as the nanograting period decreases. The FDTD-simulated results are also almost identical to those calculated by RCWA and TMM (as shown in Figs. 5d–i), indicating the accuracy of the results. The slight deviation in the transmission bands calculated by the TMM, compared to the first two methods, stems from the influence of the nanograting structure on the energy band of the dielectric multilayer film.

Fig. 5
figure 5

Simulated transmittance difference of the proposed metamaterial as a function of Bragg wavelength, the thickness of the defect layer, and the nanograting period calculated by using (a–c) FDTD, (d–f) RCWA, and (g–i) TMM (only first-order diffraction is considered) methods.

Full size image

Until now, only TM-polarized light has been discussed. In the following, we will consider the polarization dependence of the metamaterial due to the usage of one-dimensional nanograting on the top of the structure. Figures 6a–c illustrate the dependence of the transmission spectra and transmittance difference of the proposed metamaterial on the polarization angles for both forward and backward incidences. For the forward incidence, as the polarization angle of incident light increases, the short-wavelength narrowband transmission peak λ1 gradually disappears and the PC defect mode excited by the first-order diffracted transverse electric (TE) polarized light gradually appears. Due to the different reflected phase shifts in the PC for both TM and TE-polarized light, the PC defect mode excited by the first-order diffracted TE-polarized light is blue-shifted in comparison to the case of TM-polarized light (λ1), but its intensity is extremely weak. Besides, the broadband transmission peak λ3 gradually transforms into a long-wavelength narrowband transmission peak. For the backward incidence, the polarization angle has a weak influence on the transmission spectrum. Therefore, as the polarization angle increases, the total number of AOT bands for both the forward and backward incidences gradually transits from 3 to 2, as illustrated in Fig. 6c. This indicates that the metamaterial also exhibits the capability of polarization multiplexing. To explain this phenomenon, we also calculated the energy band diagram of the defective multilayer PC for TE-polarized light by using TMM, as shown in Fig. 6d. Compared with TM-polarized light, the defective multilayer PC owns a wider bandgap and narrower transmission band at a high kx under TE-polarized light. The different color star-shaped marks represent the wavelength of the FDTD-calculated transmission peak, where the red marks coincide with the defect mode resonance wavelength, further proving that the short-wavelength narrowband transmission originates from the excitation of the defect mode. The blue mark has a slight blue shift relative to the transmission band of the defective multilayer PC because the existence of the nanograting will affect the transmission band position of the defective multilayer PC, resulting in the blue shift of the transmission peak of the device. To further elucidate their resonance mechanism, the electric field distributions of the two forward transmission peaks are investigated. As depicted in Fig. 6e, the Ey of long-wavelength transmission peak also exhibits the characteristics of waveguide mode within defective multilayer PC, which results from the coupling of grating diffracted light with TE waveguide mode in the multilayer film. Figure 6f shows the Ey distribution of PC defect mode excited by first-order diffracted TE-polarized light. The characteristics of waveguide-like mode can be observed at one-dimensional nanograting, which indicates that first-order diffracted TE-polarized light excites guided-mode resonance in the one-dimensional grating. However, this guide mode is re-radiated back to the incident side due to the diffraction effect of the nanograting, manifested as a zero-order reflection of the incident light30, which further leads to the reduction of transmission intensity.

Fig. 6
figure 6

The polarization dependence of the proposed metamaterial. Dependence of transmission spectra on the polarization angle for the (a) forward and (b) backward incidences. (c) Dependence transmission differences on the polarization angle. (d) Calculated energy band diagram of the proposed metamaterial illustrated by TE-polarized incident light. (e–f) Simulated amplitude of the y-component of the electric field at the characteristic wavelengths marked in (a).

Full size image

Conclusion

In conclusion, we theoretically demonstrate an all-dielectric AOT metamaterial composed of a nanograting and a defective multilayer PC, which exhibits distinct unidirectional transmission for different incident directions. This multiband and bidirectional multiplexing AOT is realized by the coupling of defect mode and waveguide mode in the defective multilayer PC with nanograting diffracted light. Specifically, both narrowband and wideband AOT are observed for the forward incidence, while a different narrowband AOT is generated for the backward incidence. The wavelength positions and bandwidths of these transmission bands are also quantitatively described by TMM and theoretical equations. Additionally, due to its dependence on the nanograting period, Bragg wavelength, and the thickness of the defect layer, the AOT characteristics of this metamaterial can be flexibly adjusted, enabling its application in various scenarios. Furthermore, the AOT metamaterial exhibits excellent polarization multiplexing properties, with completely different unidirectional transmission bands for both TM and TE-polarized light. Due to its high unidirectional transmission, integrability, flexibility, and versatility, the proposed strategy is expected to be applied to photodiodes, filters, polarization multiplexing systems, and optical communication systems.