Introduction

In modern society, a few people suffer from pain from various causes1. In particular, the socioeconomic cost due to chronic neuropathic pain is rapidly increasing. In some cases, it has a disastrous effect on the individual patient, the family, and others around them2,3. Back and neck pain, as measured by the length of time lived with a disability, continues to be the leading cause of disability internationally, and other chronic pain conditions feature prominently in the top 10 causes of disability4.

Many studies have been conducted to measure and manage pain to handle pain-related disabilities5. Since pain itself gives various adverse health effects (sympathetic hyperactivity-induced physical changes, mental changes, and depression), it is necessary to make efforts for objective measurement and management of vital signs such as blood pressure and oxygen saturation6,7.

Although measuring pain as the fifth vital sign has limitations for improving the quality of pain management6, in the clinical area, pain management for patients with chronic neuropathic pain is the most important factor, and many attempts have been made along with drug treatment and interventional procedures. This is important not only for patient satisfaction but also for future prognosis. In particular, if severe pain experiences are repeated, there is a risk of developing severe neuropathic pain syndrome due to dendrite changes in the brain8,9. In those conditions, treatment resistance would occur10.

Therefore, to objectively manage pain, it is necessary to extract features from the viewpoint of signals outside the subjective realm of pain, and objective evaluation and related studies through pain-related biomarkers in electroencephalography (EEG) have been reported, such as power spectral analysis, alpha asymmetry, and gamma oscillations in the prefrontal, frontal and temporal area11,12,13.

Pain has four major processes: transduction, transmission, modulation, and perception14. Especially pain perception is the last process of pain process in the prefrontal cortex, which is connected with the cerebral neocortex, hippocampus, periaqueductal gray (PAG), thalamus, amygdala, and basal nuclei and accompanying changes in neurotransmitters, gene expression, glial cells, and neuroinflammation that make alterations of its structure and connectivity15.

The frontal lobe, specifically the prefrontal cortex, plays a crucial role in the perception and modulation of pain15,16. Previous studies have highlighted the involvement of the prefrontal cortex in processing pain-related information, including the sensory and emotional aspects of pain. Asymmetry features in frontal EEG signals have been shown to provide valuable insights into the lateralization of pain perception. For instance, the right hemisphere is often more involved in the emotional processing of pain, while the left hemisphere is more engaged in the sensory-discriminative aspect of pain17,18.

Gamma oscillations (30–50 Hz) are known to be associated with various cognitive and sensory processes, including attention, memory, and sensory perceptions19,20. These oscillations are believed to play a role in the integration of information across different brain regions. Studies have demonstrated that gamma activity in the prefrontal cortex is linked to the subjective experience of pain. For instance, increased gamma power in the prefrontal cortex has been observed in patients experiencing chronic pain, suggesting its involvement in pain processing13.

Recent advancements in neuroimaging and computational techniques have enabled researchers to explore the neural correlates of pain using EEG and machine learning. Several studies have demonstrated the utility of these approaches in identifying pain-related biomarkers and predicting pain severity21. Neurogenic pain was found to correlate with increased EEG power and a slower dominant frequency in patients12, and prefrontal gamma oscillations of EEG reflect ongoing pain intensity in chronic back pain patients13. This suggests that specific EEG patterns can be indicative of pain intensities.

Machine learning techniques have further enhanced the analysis of EEG data by enabling the extraction and classification of complex features. Using a nonlinear regression technique found the high allostatic load significantly correlated with worse pain and physical functioning in chronic fatigue syndrome patient patients22. Electrodermal activity and EEG were used to estimate pain intensity based on support vector machines23.

Phase-amplitude coupling (PAC) captures complex neural interactions by analyzing the coupling between different frequency bands within EEG signals, allowing us to examine how the phase of slower brain oscillations modulates the amplitude of faster oscillations24. These dynamic interactions are crucial for understanding sensory integration25, emotional processing26, and cognitive modulation27 related to pain. Unlike quantitative EEG, which focuses on spectral power within specific frequency bands, PAC provides insights into how different brain regions coordinate and communicate, reflecting network-level activity and altered functional connectivity in pain processing28. Additionally, PAC is sensitive to the dynamic states of pain, tracking variations in neural synchronization and connectivity over time, which is essential for understanding different pain conditions and responses to interventions24. By characterizing individual differences in PAC patterns, it is possible to develop personalized biomarkers of pain, enabling tailored interventions for optimized pain management based on individual neurophysiological profiles29.

While it is acknowledged that scalp EEG signals, specifically from Fp1 and Fp2 electrodes, primarily reflect cortical surface activity, the analysis of phase and amplitude relationships in these signals can provide indirect insights into deeper brain structures. Techniques from various signal processing fields, such as radar and sonar, have demonstrated that analyzing phase can enhance the detection of signals with low amplitude30,31,32. Similarly, studies in neurophysiology have shown the relevance of PAC in understanding neural dynamics. It was demonstrated that phase-locked oscillatory activity in the human brain correlates with pain perception, suggesting that phase analysis of frontal EEG signals can yield valuable information about pain processing even if it does not directly measure deep brain activity33.

By concentrating on the frontal electrodes and examining activities from theta to gamma, this study aims to enhance the understanding of pain mechanisms and contribute to the development of reliable biomarkers for pain severity. Based on previous research, we believe feature extraction is possible even if it is limited to the frontal channel, where the end of pain perception is processed. In a practical aspect, because the process of attaching multichannel EEG electrodes can be applicable by experienced medical staff, and that is also time-consuming34 if the developed algorithms support only the frontal EEG channel, it is more beneficial for clinical application. Hence, we explored the novel frontal-channel pain severity biomarkers, including spectral analysis and phase-amplitude coupling. Additionally, we utilized several machine-learning algorithms to determine their potential as predictors of pain severity.

Methods

Participants

We obtained a publicly available EEG dataset released by Monterrey Institute of Technology and Higher Education, as described in the study conducted by M. Zolezzi et al. 35. The dataset consisted of individuals suffering from chronic neuropathic pain. In total, 36 patients (28 females, 8 males) were included in the study. The participant cohort encompassed various chronic neuropathic pain conditions, including spinal cord injury (N = 11), peripheral neuropathy (N = 10), diabetes (N = 6), trigeminal neuralgia (N = 3), central nervous system (CNS) disorders (N = 3), and other conditions (N = 3). Exclusion criteria encompassed individuals with debilitating conditions such as CNS or head tumors, neurological disorders, cerebral infarction, or severe mental illness.

The study exclusively enrolled adult participants, with a mean age of 44 ± 13.98, who had been experiencing chronic neuropathic pain for at least three months. To assess the severity of pain, participants completed the Pain Detect Questionnaire, with a threshold of 12 or more for inclusion. The Brief Pain Inventory (BPI) was also utilized to evaluate pain severity36. We used the 'Actual pain' scores from the BPI questionnaire. This score was selected because it comprehensively evaluates the patient's pain intensity at the time of the survey37.

EEG data acquisition and experimental paradigm

The EEG data were acquired using a mBrain train cap with Ag–AgCl electrodes and a Smarting mBrain amplifier, following the 10–20 international system. A total of 24 electrodes (Fp1, Fp2, F3, F4, C3, C4, P3, P4, O1, O2, F7, F8, T7, T8, P7, P8, Fz, Cz, Pz, CPz, and POz) were positioned on the scalp to capture electrical activity.

The EEG signals were recorded at a sampling rate of 250 Hz. A band-pass filter ranging from 0.1 to 100 Hz was applied during data acquisition to ensure the extraction of relevant frequency components. The collected EEG data were referenced to the Cz electrode, and the left and right mastoids were used as ground electrodes.

The experimental paradigm consisted of two conditions: eyes open (EO) and eyes closed (EC). In the EO condition, participants were instructed to gaze at a white fixation cross displayed against a dark background for five minutes. Following this period, the fixation cross disappeared, at which point participants were instructed to close their eyes and maintain this closed-eyes condition for an additional five minutes. A beep sound signaled the end of the recording. In this study, we have analyzed and discussed the significant findings observed specifically in the EO condition.

EEG pre-processing

The EEG data pre-processing was performed using MATLAB R2020b (The MathWorks, Inc., U.S.A.) along with the EEGLAB38 and FieldTrip toolboxes39. Independent component analysis (ICA) was employed to remove artifacts such as muscle activity, eye movements, and line noise, thus isolating the EEG signal from the raw data38. Components identified by the ICA auto labelling, second-order blind identification (SOBI), and algorithm as muscle, eye, heart, channel noise, or line noise with a probability exceeding 70% were discarded. The signal was then re-referenced to a common average reference.

The raw signals exhibited considerable noise in the form of abnormal peaks. To effectively denoise the data, we segmented the 5 min signal into 5 s slices. Baseline correction was performed for each segment using empirical mode composition (EMD)40. This technique utilizes an iterative process of decomposing the signals into intrinsic mode functions (IMFs) and residual components, effectively eliminating the non-stationary nature of EEG signals. It begins by identifying the local minima and maxima of the signal, then using these extrema to create lower and upper envelopes and calculating their mean. The mean is subtracted from the original signal to obtain the residual.

This process is repeated: initializing the original signal, checking the number of extrema and the energy ratio of the residual signal, and sifting the residual to extract an IMF. If the energy ratio exceeds a threshold or the number of IMFs reaches a maximum limit, the decomposition stops. Subsequently, a band-pass filter with a range of 4–30 Hz was applied using a finite impulse response (FIR) filtering method.

To identify outliers, a band-pass filter with a range of 4–30 Hz was applied using a finite impulse response (FIR) filtering method. Any amplitude exceeding 100 μV was flagged as outliers, channel by channel. On average, 0.50 ± 1.89% of trials were discarded, with up to 18.33% (N = 11).

Spectral feature

To quantify the power of frequency bands, we applied filtering to the pre-processed signals within each frequency range corresponding to the four bands: theta (4–8 Hz), alpha (8–12 Hz), beta (12–30 Hz), and gamma (30–50 Hz). The power features were computed as the average of the absolute values of the filtered signals.

Furthermore, we examined the EEG power discrepancy between the left and right hemispheres of the frontal lobe. The asymmetry feature was calculated by comparing the power values at the Fp1 and Fp2 channels for each frequency band. The equation for computing the asymmetry feature is as Eq. (1).

$${\text{Asymmetry feature}} = log \left( {\frac{{\text{band power at Fp2}}}{{\text{band power at Fp1}}}} \right)$$
(1)

The frequency band was evaluated for four in the same range as the power features.

Phase-amplitude coupling feature

To examine the cross-frequency coupling between the phase of low-frequency oscillations and the amplitude of high-frequency oscillations, we employed the modulation index (MI) proposed by Tort et al.41. This measure quantifies the degree of cross-frequency coupling by utilizing Shannon entropy and Kullback–Leibler (KL) divergence. The MI is known for its robustness against noise and the ability to handle short-length signals, making it a suitable approach for analyzing PAC in EEG data41.

The pre-processed signal was subjected to band-pass filtering to isolate the desired frequency ranges for both the phase and amplitude components. Specifically, the phase frequencies were defined as theta, alpha, low beta (12–17 Hz), and high beta (18–30 Hz), while the amplitude frequencies consisted of low gamma (30–50 Hz) and high gamma (70–90 Hz). The phase of the signal and the envelope of the amplitude were then computed using the Hilbert transform applied to the filtered signal.

Regression analysis

The regression analysis using EEG features was conducted utilizing a Python toolbox. The analysis aimed to examine the relationship between pain and quantified EEG features. Pain levels were determined based on a questionnaire completed by the subjects, specifically focusing on the ‘Actual Pain’ score in the BPI questionnaire among several surveys. In this study, we employed five regression models: linear regression, random forest regression, and support vector regression (SVR) models using linear, polynomial, radial basis function (rbf) kernels. The brief descriptions of the five models are explained as below.

Linear Regression: The linear regression is a powerful statistical method used to investigate the relationship between a dependent variable and one or more independent variables42. Its objective is to estimate the parameters of a linear equation that best fits the observed data. The linear regression model can be expressed as Eq. (2).

$$y = { }\beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \cdots + \beta_{n} x_{n} + \varepsilon { }$$
(2)

\(y\) represents the dependent variable, pain score, \({x}_{n}\) are the independent variables, calculated features, and \(n\) is the number of features. \({\beta }_{n}\) denotes the regression coefficients for the intercept and independent variables, respectively. It estimates the regression coefficients using ordinary least squares (OLS), and \(\varepsilon\) is the error term, representing the unexplained variability in the dependent variable.

Random Forest Regression: Random forest regression is an ensemble method using multiple decision trees that are trained on a random subset of the data43. In this study, we utilized the ‘sklearn.ensemble’ package in Python, specifically the ‘RandomForestRegressor' class, to perform the estimation. The random forest regression model can be expressed as Eq. (3).

$$\hat{f} = { }\frac{1}{B}\mathop \sum \limits_{b = 1}^{B} f_{b} \left( {x^{\prime}} \right)$$
(3)

\(B\) represents the number of iterations of randomly selecting samples and corresponds to the number of trees, \({f}_{b}\) is the regression tree trained with randomly selected \(x\), and \(\widehat{f}\) s the prediction value and represents the average of the predictions of all individual regression trees on the test sample \({x}{\prime}\) after training in Eq. (3). We set the maximum depth of the tree as 3.

Support Vector Regression: Support vector regression is a modelling technique employed to capture nonlinear relationships between a dependent variable and independent variables by leveraging support vector machines44. In this study, we utilize the 'sklearn.svm.SVR' library to estimate the SVR model. The SVR model is represented as Eq. (4).

$${\text{y}} = { }w^{T} \phi \left( x \right) + b$$
(4)

\(\phi \left(x\right)\) denotes a nonlinear function that projects the calculated features \(x\) into a high-dimensional feature space, \(w\) is the weight vector of the hyperplane, and \(b\) represents the bias value of the hyperplane. The main advantage of SVR lies in its ability to use kernel tricks to identify hyperplanes within the transformed feature space, thereby effectively capturing complex non-linear relationships between variables.

We explore the effectiveness of three distinct kernel functions: linear, polynomial, and radial basis functions. Each kernel function provides a different approach to identifying the similarity between data points in the high-dimensional feature space. This enables SVR to handle various types of non-linear relationships present in the data and enhance its predictive capabilities for regression tasks.

All 20 features were included in the analysis, consisting of eight band powers, four power asymmetries, and eight PAC asymmetries. Consequently, each model was evaluated using all possible combinations of features, resulting in a total of 1,048,575 (\(={\sum }_{k=1}^{20}{}_{20}{\complement }_{k}\)) combinations.

To assess the performance of the regression models, R-squared was utilized as the evaluation criterion as Eq. (5) Ref.45. The performance was evaluated using a leave-one-subject-out approach, where each subject's data was excluded from the analysis to test the model's predictive ability.

$$R^{2 } = 1 - \frac{{\sum \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\sum \left( {y_{i} - \overline{y}} \right)^{2} }}\user2{ }$$
(5)

\({y}_{i}\) is the true pain score, the actual pain score is the predicted score, and y is the mean of true label data of the pain score.

Statistical analysis

We utilized Pearson’s linear correlation coefficient to examine the association between pain scores and EEG features, as pain scores are represented as a sequence indicator ranging from 0 to 10. To compute reliable correlation coefficients, we utilized Cook's Distance to remove outliers46. A threshold of 85%, based on the percentile-based of Cook's Distance, was employed. This ratio referenced the proportion of outliers detected within the feature data distribution.

To validate the model, we generated surrogate data to examine the chance level. We generated 1000 surrogate data by randomly shuffling the label dataset, keeping the label proportions uniform. The dataset consists of 36 subjects, and there are 3.46 × 1029 permutations possible given the overlapping labels, which gives us a sufficient amount of data. We recalculated the regression models on the surrogate datasets for each combination of EEG features in each model. The chance level we reported is the average of 1000 datasets of sham data, and we found it to be statistically significantly different from the actual result (T-test, p < 0.001).

Results

Correlation between EEG features and pain score

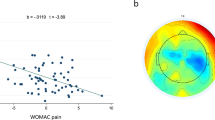
Figure 1 presents the band power indices in the theta (4–8 Hz), alpha (8–12 Hz), beta (12–30 Hz), and gamma (30–50 Hz) frequency bands for the Fp1 and Fp2 channels, along with the asymmetry power feature of the frontal lobe. The data point in scatter plots depicts a subject with their corresponding actual pain score. The statistical analysis was performed using Pearson’s correlation to examine the relationship between the power features and the pain score.

Fig. 1
figure 1

Band power (top two rows) and asymmetry indices (bottom row). The results of Theta, Alpha, Beta and Gamma are presented from the left to the right columns. In each figure, dots represent patients, with triangles indicating participants identified as outliers based on Cook’s distance, and circles representing data included in the correlation coefficient calculation. The fitted line is provided with the corresponding correlation coefficient and p-value (red: significant p < 0.05, gray: non-significant).

Full size image

The results indicate that there is no significant correlation between the power features of individual channels and the pain score. However, the asymmetric feature calculated for the beta and gamma bands showed a significant correlation with the pain score (beta: r = -0.398, p = 0.027/gamma: r = −0.435, p = 0.02).

Figure 2 represents the PAC feature, which is modulation index, of Fp1 and Fp2, and asymmetry PAC feature of the frontal channels with the pain score. The PAC is calculated from the phase in the theta, alpha, low beta (12–17 Hz), and high beta (18–30 Hz) and the amplitude in the low gamma (30–50 Hz) and high gamma (70–90 Hz) frequencies. There is only a correlation of PAC between the phase of low beta and the amplitude of the low gamma frequency (r = −0.413, p = 0.021).

Fig. 2
figure 2

PAC (top four rows) and asymmetry (last two rows) indices. Theta, Alpha, Beta and Gamma results are presented from the left to right columns. In each figure, dots represent patients, with triangles indicating participants identified as outliers based on Cook's distance, and circles representing data included in the correlation coefficient calculation. The fitted line is provided with the corresponding correlation coefficient and p-value (red: significant p < 0.05, gray: non-significant).

Full size image

Figure 3 demonstrates the correlation coefficient between the pain score and the extracted EEG features. Notably, the analysis reveals that asymmetric features exhibit notably higher absolute R values on average than band power or PAC features. Particularly, this tendency is more dramatic in PAC features. As shown in Fig. 3, |r| of PAC (Fp1) and PAC (Fp2) are 0.032 and 0.045, but the PAC asymmetry feature shows |r|= 0.203 on average.

Fig. 3
figure 3

Absolute values of correlation coefficients (|r|) of EEG features. Circles represent the power and power asymmetry indices, squares represent the PAC of the low gamma amplitude, and triangles represent the PAC of the amplitude of the high gamma amplitude. The gray bars are the average of the values for each channel and asymmetry.

Full size image

Regression analysis of pain score

A total of five models were used in the regression analysis between EEG features and pain scores. The features utilized were the power feature, power asymmetric feature, and PAC asymmetric feature. Figure 4A illustrates the aligned R-squared values for all possible combinations of these features. Following this, the performance of the models followed in this order: support vector with RBF kernel (0.3332), random forest (0.2339), support vector with linear kernel (0.1837), linear (0.0347) regression models (Fig. 4b–e).

Fig. 4
figure 4

Results of regression analysis. (a) Performance of each regression model is presented as a function of feature combination cases sorted on R-squared value. (b–f) The best case of each model is shown. Dots represent the pain scores of the subjects predicted by each model, and the black line represents the actual pain scores of the subjects. The correlation coefficients of each model are presented in parentheses, and ch denotes the statistical chance level of the best features. The chance levels were computed by averaging the \({R}^{2}\) values over 1000 random shuffling of labels. The asterisk (*) indicates statistical significance meaning that the performance is different from the statistical chance level, as confirmed using a one-sample t-test (p < 0.01).

Full size image

When the appropriate feature combination is selected, the support vector regression model using polynomial kernel demonstrates the highest performance. Figure 4F displays the predicted and actual values of this top-performing with an R-squared value of 0.6555.

Figure 5 presents the feature combinations chosen based on the R-squared values of the second polynomial regression. The top four most frequently selected features, in descending order, are as follows: PAC asymmetric feature (theta phase-low gamma amplitude), power asymmetric feature (gamma), PAC asymmetric feature (low beta phase-high gamma, low beta phase-low gamma).

Fig. 5
figure 5

R-squared values (bottom) and selected features (top) in Support Vector Regression model using a polynomial kernel. Only cases showing positive R-squared values (larger than 0) were presented, and the cases were sorted on the performance. The right figure presents the counts, that is, the number of selections per feature.

Full size image

Looking more closely, based on an \({R}^{2}\) of 0 or higher in Fig. 5 (total number = 107,954), the number of times (or percentage) a feature is selected, are 99,906 (92.54%) for PAC asymmetric feature of theta phase-low gamma amplitude, 54,508 (78.28%) for power asymmetric feature of gamma, 83,569 (77.41%), and 72,302 (66.97%) for PAC asymmetric feature of low beta phase-high gamma and low beta phase-low gamma.

Discussion

This study, involving patients with chronic neuropathic pain of various pathophysiological mechanisms, aimed to identify common EEG biomarkers to assess pain severity despite the heterogeneity. The patient group included conditions such as spinal cord injury, peripheral neuropathy, diabetes, trigeminal neuralgia, and central nervous system disorders. However, we highlights common processes in chronic pain, such as central sensitization, neuroplasticity, emotional and cognitive components, and neuroinflammation. These processes can be detected through specific EEG patterns. By analyzing EEG activity recorded from frontal channels, this study contributes to identifying biomarkers that can reliably indicate pain severity across different neuropathic pain conditions.

In order to objectively quantify subjective pain from the signal processing domain, heart rate variability (HRV) and electrical dermal activity (EDA) have been used47,48,49, and there are commercialized products that have been applied in clinical field50. In addition, there have been papers that have analyzed pain intensity with EEG characteristics in the frontal lobe and temporal lobe12,13,51.

Functionally, it has recently been revealed that the prefrontal and frontal lobe is the main region in the final processing of pain perception15,52,53. Therefore, for the first time to the knowledge of the authors, in our study, we focused on the prefrontal Fp1 and Fp2, and applied several feature extracting algorithms for finding pain related biomarkers, and finally predicted pain severity through several regression models.

Similar to the reports of previous studies that the alpha band power of the frontal lobe was related to the severity of pain12,34, statistically significant features were observed in the pain score and the Pearson correlation in the frontal lobe the beta and gamma band in EO in our study.

There have been many reports on alpha power asymmetry of the left and right sides of the EEG in depressed patients54,55. It has also been reported in pain patients11. However, no statistically significant alpha asymmetric features were observed in our study. In the case of patients with chronic neuropathic pain, it is assumed that there was a difference in terms of acute pain related EEG changes or chronic depression related cortical suppression in previous alpha asymmetry related reports.

Phase amplitude coupling is the algorithms that reflect the characteristics of brain waves, and is known to represent the characteristics of signal transfer between a function in a local region and a distal region56. PAC has been reported in various brain areas including the prefrontal cortex57,58 in electrophysiological recordings.

Alpha oscillations are associated with pulses of cortical inhibition every ~ 100 ms59,60, whilst supporting communication through phase dynamics61. In contrast, gamma oscillations emerge through local excitatory and inhibitory interactions, and synchronize local patterns of cortical activity62,63.

In particular, PAC related with general mechanism for memory processing and synaptic plasticity64. For example, encephalopathy severity can be stratified with PAC65 or in dementia patients, the characteristics of changes in theta gamma PAC have been reported as a major biomarker of disease, and the characteristics of changes that early stages of Alzheimer dementia elicit a region-specific decrease of PAC in the neural activity66.

In our study, a statistically significant correlation was observed between the asymmetry feature of low beta phase and low gamma amplitude coupling and pain intensity. Additionally, based on the R-values of correlation coefficients (|r|> 0.24), the asymmetry features of the theta phase and low gamma amplitude coupling, and low beta and high gamma amplitude coupling are also expected to be associated with pain scores. The authors believe that there is a novelty in that we found these EEG-based pain features, particularly asymmetry, in pain-related studies.

In this study, we conducted a machine learning regression analysis to explore the potential use of biomarkers for predicting pain in clinical applications. We employed a total of five different models, each employing a distinct approach. Linear regression works well when there is a linear pattern between features and pain scores, while support vector regression and random forest regression are better suited for non-linear patterns or more complex relationships. We verified the assumptions of the linear regression model by examining the Q-Q (quantile–quantile) plot for residuals. The Q-Q plot compares the distribution of residuals with the theoretical normal distribution, showing how closely the two distributions match67. We found that most data points in the plot aligned closely with the diagonal line, indicating that the residuals followed a normal distribution well.

Utilizing a polynomial kernel, the support vector regression model exhibited the best overall performance, while the linear regression model demonstrated the lowest performance. These results suggest that pain is not only associated with complex features, such as the PAC and the asymmetry features, but also characterized by complex relationships between these features.

Upon examining the features selected for the high-performing support vector regression model, Fig. 5 indicated that the top four features were all asymmetric features, providing further support for the complexity of the biomarker of pain intensity. Remarkably, these features align with the earlier findings in (Fig. 3), as they showcased relatively higher absolute values of correlation coefficients (|r|> 0.24): PAC asymmetric feature (theta phase-low gamma amplitude, low beta phase-high gamma and low beta phase-low gamma) and power asymmetric feature (gamma).

We compared the three kernels in support vector regression and found that each model performed significantly differently. Because support vector regression solves high-dimensional data nonlinearly by a kernel function, it is important to choose the right function for optimal performance68,69. We compared linear, polynomial, and RBF kernels, and while all three models performed better than simple linear regression, the polynomial kernel had the highest performance. This suggests that the EEG features associated with pain intensity have non-linear relationships and complex patterns. The poly kernel function models this complexity well, providing high accuracy and generalizability.

To ensure that there was no overfitting due to the limited number of data and to validate the computed statistical values, we generated sham data. The results from the sham data help verify whether our model's performance occurred by chance. The 1,000 generated datasets formed a Gaussian distribution, indicating that the data was appropriately generated (Supplementary Fig. S1). The mean of the sham's distribution was statistically significantly different from real data, and the results of the real were much more positive (p < 0.01). Additionally, to evaluate the impact of the number of features on the models, we generated fake data by randomly selecting the same number of features as the optimal number for each model. This result also showed that our outcomes were significantly superior (Supplementary Fig. S2). Therefore, we confirmed that our findings were not biased by the model or the number of features.

The first limitation of this study is the restricted patient group due to the use of a previously public dataset. The number of patients in the data was insufficient; it included only participants from a single institution and a single race (Mexican), and the gender ratio was also imbalanced. It consisted of 8 males and 28 females, and we observed differences in pain scores, with males averaging 6.75 ± 2.05 and females averaging 4.78 ± 2.61, indicating a difference in a difference in distribution.

The second limitation is the inclusion of participants with mild pain. One of our study's limitations is including pain scores below 3, as they are typically not indicative of significant clinical pain. To enhance the clinical relevance of our results, future studies should consider excluding these lower pain scores to ensure a more precise assessment of a clinically significant pain cohort. The first and second limitations also highlight the need for follow-up studies with larger cohorts.

The third limitation of this study is the variation in impacts of different chronic pain disorders on sensory, affective, and cognitive domains. Previous studies have shown that distinct pain disorders result in varied degrees of central sensitization, reorganization, and emotional/cognitive dysfunctions70,71. These differences may influence the EEG biomarkers identified in this study, suggesting that future research should consider the specific characteristics of various pain disorders when developing and validating pain assessment models.

The four limitation is that PAC was performed in a local area. Considering the perspective of signal transmission between distal regions, the analysis limited to the PAC in the local region was inevitable, considering that EEG channels limited to the frontal lobe were used considering the practicality of future clinical applications. However, in the future, we will develop research to see if additional characteristics can be found by analyzing the PAC between the EEG channels between the left and right hemispheres. Moreover, with additional subjects through Asian patients, it is expected that common characteristics between races can be confirmed, and the generalization performance of the developed model can be verified.

A further limitation is the potential lack of generalizability of our model. While surrogate techniques were employed to validate our findings, the model was developed using a specific dataset, which may not fully represent the broader population. Future studies should aim to validate the model with larger and more diverse cohorts to enhance its generalizability and clinical applicability.

Despite these limitations, this study intensively analyzed the EEG characteristics under the frontal region limited relation with the severity of pain. It is novel in that the biomarker was found by applying the PAC method, and it has the strength of attempting pain severity regression for future clinical application.