Quantum-assisted federated intelligent diagnosis algorithm with variational training supported by 5G networks

Abstract

In the realm of intelligent healthcare, there is a growing ambition to reshape medical services through the integration of artificial intelligence (AI). However, conventional machine learning faces inherent challenges such as privacy issues, delayed updates, and protracted training times, particularly due to the hesitance of medical institutions to directly share sensitive data, with possible noises. In response to these concerns, a Quantum-Assisted Federated Intelligent Diagnosis Algorithm ($\beta$-QuAFIDA) is proposed, applied into real medical data. Leveraging the capabilities of the 5G mobile network, this approach works the connection between Internet of Medical Things (IoMT) devices through the 5G, synchronizing training and updating the server model without disrupting their real-world applications. In our quest to safeguard patient data and enhance training efficiency, our study employs an innovative heuristic approach marked by a nested loop structure. Specifically, the inner loop is dedicated to training the beta-variational quantum eigensolver ($\beta$-VQE) to approximate the expectation values of the proposed algorithm; the outer loop trains the $\beta$-QuAFIDA to reduce the relative entropy towards the target. This approach involves a balance between privacy considerations and the urgency of training. Results demonstrate that representations with low-rank attained through $\beta$-QuAFIDA offer an effective approach for acquiring low-rank states. This research signifies a step forward in the synergy between AI and 5G technologies, presenting a novel avenue for the advancement of intelligent healthcare.

Introduction

In the realm of intelligent healthcare, there is a growing ambition to reshape medical services through the integration of artificial intelligence (AI). However, conventional machine learning faces inherent challenges such as privacy issues, delayed updates, and protracted training times, particularly due to the hesitance of medical institutions to directly share sensitive data, with or without noises. In response to these concerns, Federated Learning (FL) has emerged as a promising paradigm that allows model training across decentralized devices without sharing raw data. Additionally, FL, has other benefits, such as in preserving privacy, and the ability to train models in distributed environments¹.

Despite the advantages of FL, it is essential to acknowledge the existing drawbacks, especially in the context of healthcare applications. The decentralized nature of FL introduces communication overhead, vulnerability to model inversion attacks, and potential for biased models. Moreover, FL may suffer from slow convergence and increased computational costs as the number of participating devices grows².

However, Quantum computing has also found applications in intelligent healthcare. The significant promise of Quantum computing lies in its potential for exponential speedup through quantum algorithms compared to classical methods, paving the way for transformative advancements in healthcare-related computations.

In the realm of intelligent healthcare, quantum computing has performing tasks, such as optimizing complex algorithms, simulating intricate biological systems, or efficiently solving linear systems of equations. The unique computational capabilities of quantum algorithms bring forth the prospect of enhancing medical simulations, accelerating data analysis in healthcare research, and optimizing the processing of vast datasets.

Current quantum devices encounter notable limitations, marked by limited qubit counts and inherent noise processes that restrict circuit depth. To address these challenges, Variational Quantum Algorithms (VQAs) have emerged as a leading strategy. VQAs utilize classical optimizers to train parameterized quantum circuits, offering a crucial method to alleviate the constraints imposed by existing quantum devices. Thus, this means that VQAs help overcome the current limitations of quantum computers by optimizing their performance using classical methods, making quantum computing more practical and accessible for various applications.

The integration of VQA represents a groundbreaking frontier in the intersection of quantum computing and machine learning. VQA leverages the principles of quantum mechanics to perform computations that traditional classical algorithms may find challenging or infeasible. By intertwining variational methods with quantum circuits, VQA introduces a powerful approach for solving optimization problems, machine learning tasks, and simulations³.

This integration holds the promise of unlocking unprecedented computational capabilities, potentially outperforming classical counterparts in specific domains. The exploration of VQA is at the forefront of research, with ongoing efforts to harness quantum parallelism and entanglement for enhanced problem-solving and optimization. In this rapidly evolving landscape, the integration of VQA opens avenues for novel applications, from improving optimization processes to advancing machine learning methodologies in a quantum paradigm.

Variational Quantum Neural Networks (VQNNs) emerge as a stride in the convergence of quantum computing and machine learning. VQNNs extend the capabilities of VQA by introducing a neural network structure into quantum circuits, enabling the incorporation of trainable parameters. This unique fusion of quantum and neural network architectures holds the potential to revolutionize the landscape of quantum-enhanced machine learning.

VQNNs introduce adaptability and learning capabilities to quantum circuits, allowing them to evolve and optimize their performance for specific machine learning tasks. By leveraging the variational principles within quantum circuits, VQNNs offer a versatile platform for tackling complex optimization problems, enhancing machine learning models, and conducting simulations in a quantum environment.

In this article, the challenges and limitations of FL are treated, with a specific focus on its application in intelligent healthcare. Additionally, the integration of VQA into the FL framework is explored, aiming to leverage the capabilities of quantum computing for enhanced privacy, accelerated convergence, and improved model generalization.

The healthcare domain poses unique challenges for FL due to the sensitive nature of patient data. Privacy concerns often hinder the willingness of medical institutions to collaborate and share data directly. This reluctance, in turn, impacts the effectiveness of FL in achieving robust and generalized models for medical diagnosis and prognosis.

Furthermore, the deployment of FL in healthcare is intricately connected with the communication between devices using 5G technology. The communication between Internet of Medical Things (IoMT) devices is crucial for the success of FL in healthcare applications. The low-latency and high-bandwidth characteristics of the 5G network play a pivotal role in facilitating seamless communication among distributed medical devices.

To address the challenges of FL in healthcare, a novel approach is proposed, termed $\beta$-Quantum-Assisted Federated Intelligent Diagnosis Algorithm ($\beta$-QuAFIDA). The $\beta$-QuAFIDA incorporates VQA to enhance the FL framework, allowing for secure and efficient model training. Utilizing the 5G mobile network, our approach establishes robust connections between IoMT devices, enabling the collaborative training of quantum-enhanced models. The $\beta$-QuAFIDA tailors datasets for patients diagnosed with specific medical conditions, ensuring synchronized training and updating of server model without disrupting real-world applications.

Coverage of article and contributions

In response to the challenges, such as provide a win-assisted healthcare system, preserve patient privacy, predict diagnostics for increasing their accuracy, use of quantum computing, which ensures the data security between pars, and propose a framework with a 5G communication, our study proposes the $\beta$-QuAFIDA with Variational Training. Leveraging the 5G mobile network. This not only accelerates the generation of vital medical data but also significantly reduces communication times within the federated learning process.

The $\beta$-QuAFIDA is meticulously crafted to cater specifically to patients diagnosed with distinct medical conditions, ensuring synchronized training and updating the server model without disrupting real-world applications. As we prioritize safeguarding patient data and optimizing training speed, our methodology employs a heuristic approach characterized by a nested loop. The inner loop utilizes the $\beta$-variational quantum eigensolver ($\beta$-VQE) to approximate the expectation values, while the outer loop trains to minimize relative entropy to the target. This delicate balance between privacy considerations and the urgency of training forms the cornerstone of our methodology.

Our findings underscore the efficiency of low-rank representations obtained by $\beta$-VQE in learning low-rank target states, covering classical data and low-temperature quantum tomography. Rigorous testing of our method on both classical and quantum data, demonstrates the ability to obtain a high fidelity model. This research represents a significant step toward variational training of models, ushering in new possibilities at the intersection of AI and 5G technologies for the advancement of intelligent healthcare.

In simple terms, our research proposes a method using advanced technologies like quantum computing and 5G communication to improve healthcare by securely sharing patient data for better diagnostic accuracy, all while ensuring patient privacy and reducing communication times.

The primary contributions of this paper are outlined as follows:

• Introduction to a quantum federated learning framework, specifically crafted for intelligent diagnosis within 5G mobile networks. The $\beta$-QuAFIDA model’s accuracy remained consistent even in noisy environments.

• Mitigation of computational costs through the $\beta$-Variational Quantum Eigensolver Optimization process.

• Exploration of the encoding classical method information into quantum states, though the Quantum Circuit Optimization process.

The proposed framework utilizes the beta-Variational Quantum Eigensolver Optimization technique, a specific quantum computing approach tailored for optimizing tasks within the healthcare system models. This technique operates by leveraging quantum principles to select the most relevant quantum states with the highest probabilities, thereby enhancing computational efficiency and convergence rates compared to classical machine learning methods.

One of the key advantages of employing quantum computing techniques like beta-Variational Quantum Eigensolver Optimization over classical machine learning methods lies in their inherent ability to exploit quantum parallelism and entanglement. Quantum parallelism allows for the simultaneous evaluation of multiple possibilities, leading to potentially exponential speedup in certain computational tasks. Additionally, entanglement enables quantum systems to represent and process information in ways that are not feasible with classical approaches, thereby unlocking new avenues for optimization and problem-solving.

Furthermore, the use of quantum techniques like beta-Variational Quantum Eigensolver Optimization offers advantages in handling complex optimization problems commonly encountered in healthcare system models. By efficiently navigating through high-dimensional parameter spaces and selecting optimal solutions, these quantum approaches can significantly enhance the performance and scalability of healthcare analytics compared to classical methods.

The following sections in this document are structured as follows: Related works offers insights into the existing body of work in the field, whereas Proposed System Model section elaborates on the procedural aspects of the $\beta$-QuAFIDA. Performance Evaluation section showcases the outcomes of experiments conducted with the $\beta$-QuAFIDA algorithm. Ultimately, Discussions and Conclusions sections serve for summarizing the key findings of our work, offering a potential view into future research possibilities in this field.

Related works

The FL in healthcare has been proposed with a focus on preserving patient privacy data in remote monitoring systems⁴. Additionally, FL can be seen as a machine learning (ML) framework designed to address privacy concerns associated with acquiring authentic data⁵. Throughout the training, individuals participate in sharing model-related data without directly disclosing their personal information. Alternatively, they send their model parameters to a centralized server, which consolidates and returns refined parameters for local model refinement⁶.

While this process leverages data contributions from all participants, transmitting model parameters alone may introduce potential privacy risks. In response to certain apprehensions, a variety of methods are utilized, such as secure aggregation, homomorphic encryption, and additional privacy safeguarding techniques⁷.

The application of FL in smart healthcare offers intelligent and privacy-enhanced health services. FL is anticipated to play a pivotal role in establishing large-scale collaborative healthcare systems, transitioning from centralized health data analytics to distributed healthcare operations with privacy awareness. Zhang et al.⁸ introduced a privacy-preserving system for diagnosing Alzheimer’s disease.By employing an approach based on Federated Learning (FL), the system gathers user audio data via Internet of Things (IoT) devices situated in smart home environments, thereby ensuring the integrity of data and confidentiality of models. Another framework⁹ is designed for smart healthcare, in which it offers a privacy-preserving method to evaluate FL participants’ contributions, optimizing the FL model aggregation approach based on these evaluations.

Quantum Federated Learning (QFL), an evolving domain within Quantum Machine Learning (QML), integrates traditional FL into the quantum scenarios. Ma et al.¹⁰ proposed QFL implementation utilizing blind quantum computing guarantees data security between pairs. Empirical findings demonstrate the efficacy of blind quantum computing in achieving QFL. However, it presents some challenge¹⁰, such as implement a hybrid QML algorithm¹¹. Nowadays, these implementations are not deeply explored in diverse scenarios and dataset.

For instance, studies have investigated the impact of noise in quantum federated computing¹², aiming to mitigate its effects on model performance and convergence. Additionally, the optimal number of Quantum Clients¹³ and the configuration of distributed quantum systems have been topics of interest, with researchers exploring different architectures to maximize efficiency and scalability.

In the context of healthcare applications, related works have focused on leveraging Variational Quantum Eigensolver (VQE) Optimization techniques¹⁴. These studies aim to optimize quantum circuits and algorithms for efficient processing of medical data, thereby enhancing the accuracy and reliability of predictive models in healthcare settings. However, the methods obtained an accuracy not superior to 85%.

Furthermore, the selection and preprocessing of datasets play a crucial role in the success of QFL algorithms. Researchers have explored various strategies for dataset curation and augmentation to ensure robust model training and generalization across different healthcare domains¹⁵. Additionally, efforts have been made to develop privacy-preserving techniques compatible with quantum computing frameworks¹⁶, ensuring the confidentiality and integrity of sensitive medical data in federated learning environments.

Expanding on the previous research, this study introduces a novel QFL algorithm and employs it to analyze medical data for intelligent diagnosis in 5G mobile networks.

Proposed system model

The architectural framework for the healthcare system is simulated to work with IoMT devices, communicating though 5G mobile network. This methodology ensures uninterrupted monitoring of patients’ health conditions, providing timely updates to our machine learning model, the $\beta$-QuAFIDA, without perturbing its real-world counterpart.

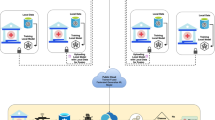
In Figure 1, the decentralized training paradigm QFL process is shown. FL begins with a global model $\Theta \in {\mathbb {R}}^n$, and the model is sent to N local clients as identical copies $\Theta _1, \ldots , \Theta _K$, where $\Theta = \Theta _1 \cdot \ldots \cdot \Theta _K$ represents the model parameters for the entire model. Subsequently, a client $j \in [N] = \{1, \ldots , N\}$ with a local model $\Theta _j$ engages in local training for a customizable number of epochs to derive a new (private and local) model $\Theta _{ej} \ne \Theta _j$. The set of trained client models $\{{\Theta _{ej}}_{j=1}^{N}\}$ is then aggregated to form a new global model $\Theta _e$, replacing the initial $\Theta$ to complete one FL cycle. This process iterates over several rounds.

Thus, the process shown in Figure 1 involves training a global model that is then sent to multiple local clients for further training. Each client improves the model based on its local data, and the updated models are then combined to create a new global model. This cycle repeats over several rounds, improving the overall model with each iteration.

In the proposed framework, local clients function as quantum simulators. In which, circuit parameters undergo training via a hybrid quantum-classical approach. During each training round, a designated number of client nodes are chosen to execute the local training. Following the completion of client training, the central node aggregates circuit parameters from all client nodes. For model aggregation, it is used the mean of the client models. The simulation framework, illustrated in Figure 1, in which the patients’ data are stored in a secure dataset and only the parameters updates are transmitted to the global server.

In this work, the Quantum Exact Simulation Toolkit (QuEST)¹⁷. It is an open source, hybrid multithreaded GPU accelerated simulator of quantum circuits.

Fig. 1

Proposed $\beta$-Quantum-Assisted Federated Intelligent Diagnosis Algorithm ($\beta$-QuAFIDA) model applied in a healthcare system using 5G communication between IoMT devices.

The simulation framework, as depicted in Figure 2, seamlessly integrates the QuEST for quantum circuit simulation, PennyLane¹⁸ with PyTorch for Variational Quantum Neural Networks (VQNNs) and $\beta$-Variational Quantum Eigensolver Optimization ($\beta$-VQE), followed by the Quantum Circuit Optimization. The framework also employs the FLSim tool¹⁹ to simulate the Federated Learning, enhancing the synergy between quantum and classical methodologies for optimized models in intelligent healthcare applications. The integration stage ensures efficient collaboration, while the Federated Learning Simulation reflects decentralized training practices, crucial for preserving medical data privacy. Pysim5G, a Python Simulator for Integrated Modelling 5G²⁰, is used to simulate the integration of 5G with the Internet of Medical Things (IoMT). The iterative Simulation Execution captures the dynamics of the integrated model, including Quantum Circuit Optimization and $\beta$-VQE Optimization, while subsequent analysis and evaluation provide insights into its effectiveness and impact on advancing intelligent healthcare solutions.

Fig. 2

Simulation framework integrating QuEST, PennyLane with PyTorch, Quantum Circuit Optimization, $\beta$-VQE, Federated Learning, and IoMT with 5G using Pysim5G.

The proposed algorithm involves two types of participants: Quantum clients with a local data and a server. A medical facility equipped with quantum-computing capabilities is referred to as a Quantum Client. Each Quantum client possesses local data and the algorithm, while the server maintains global parameters. The procedure comprises the following steps:

• 1. The server randomly selects n Quantum clients to participate in training, broadcasting initial parameters to the Quantum clients. After receiving these parameters, each Quantum client initializes its local VQNN, commences local training process, and updates its parameters accordingly.

• 2. Subsequently, the server gathers the parameters sent back from the Quantum clients, aggregates them, and then redistributes the aggregated parameters to all participants.

• 3. The first two steps are repeated until termination conditions are satisfied, e.g., the loss function reaching a specific threshold value.

• 4. Upon reception of the final parameters from the server, all Quantum clients proceed to utilize them for further training iterations.

In the Quantum client is employed quantum circuits constructed using quantum gates to acquire patient diagnosis results through simulations. A well-structured algorithm comprises linear and nonlinear components. Single-qubit rotation gates and Controlled-NOT (CNOT) gates form the linear part, and non-trace-preserving quantum operations form the nonlinear part.

The training process involves the step of initializing the VQNN, in which parameters received from the server are used to initialize the local network. After occurs the data encoding into quantum states. The Quantum evolution ocurrs, in which the quantum state evolves through a quantum circuit. The training of the VQNN occurs, where the Quantum clients train their local network by performing local iterations and updating parameters using a local update algorithm.

This process uses quantum circuits to simulate patient diagnosis results, with quantum gates performing calculations and updates to improve the model.

The training process employs the margin loss function, represented by (1).

$$\begin{aligned} \text {Loss function} = {\left\{ \begin{array}{ll} d(r_p, r_a), & \text {positive pair} \\ \max (0, m - d(r_n, r_a)), & \text {negative pair} \end{array}\right. } \end{aligned}$$

(1)

Here, $r_a$, $r_p$, and $r_n$ are the sample representations of $x_a$, $x_p$, and $x_n$.

The server has two main tasks: initializing a set of parameters for Quantum clients and aggregating parameters returned by Quantum clients using the global update algorithm.

The objective is to optimize the global loss function, as shown in the following:

$$\begin{aligned} L(\theta ) = \sum _{k=1}^{n} \omega _k {\mathcal {L}}(\theta ; Z_k) \end{aligned}$$

(2)

Where $\omega _k$ represents the ratio of data per Quantum client to the total data, and $Z_k$ denotes the sample of data stored in the k-th Quantum client.

The parameters returned by Qauntum clients are aggregated using the weighted average algorithm, as given in Eq. (3).

$$\begin{aligned} \theta _{\text {avg}} = \sum _{k=1}^{n} \omega _k \theta _k \end{aligned}$$

(3)

The proposed algorithm is constructed using PennyLane²¹, a Python library designed for quantum machine learning, and PyTorch to implement the proposed algorithm and process the medical data. The approach taken is synchronous, which necessitates the server to await the completion of local iterations by each participating Quantum client and the subsequent return of their parameters. Only after all Quantum clients have provided their parameters does the server proceed to aggregate them.

The proposed $\beta$-QuAFIDA utilizes the capabilities of FL while integrating quantum computing techniques. QFL expands the capabilities of classical FL into the realm of quantum computing.

Quantum circuit optimization

The goal of the optimization is to perform a combination of classical and quantum information processing. The classical-to-quantum encoding is a crucial preparatory step for successful integration of classical and quantum components in healthcare applications.

The structure of the quantum circuit is defined as follows. The quantum functions employed should have a definite gradient, as depicted in:

$$\begin{aligned} \nabla _{\theta _i} f(x; \theta ) = \langle x | \nabla _{\theta _i} L_{\theta _i}^{(bB)} | x \rangle , \end{aligned}$$

(4)

where, the gradient can be expressed as the sum of identical linear transformations. $\nabla _{\theta _i} f(x; \theta )$ represents the gradient of the function f with respect to the parameter $\theta _i$; x is the input variable; $\theta$ represents the set of parameters of the quantum circuit; $L_{\theta _i}^{(bB)}$ denotes a quantum operator parameterized by $\theta _i$ and involving some observable denoted by bB; $\langle x |$ and $| x \rangle$ denote the braket notation representing the state x.

Furthermore, the input state is obtained by combining the first $i-1$ unitary transform with the input unitary transform:

$$\begin{aligned} | \psi _{i-1} \rangle = bU_{i-1}(\theta _{i-1}) \ldots bU_1(\theta _i) bU_0(x) | 0 \rangle . \end{aligned}$$

(5)

where, $| \psi _{i-1} \rangle$ represents the input state obtained after applying the unitary transforms; $bU_{i-1}(\theta _{i-1}) \ldots bU_1(\theta _i) bU_0(x)$ denotes a sequence of unitary transformations parameterized by $\theta _{i-1}$ to $\theta _1$ and applied to the input state $| x \rangle$; $| 0 \rangle$ represents the initial state of the quantum system.

Subsequently, all gates are combined after the $i$-th unitary transformation with the observable $bB$ to obtain a new observable $bB_{i+1}$.

$$\begin{aligned} bB_{i+1} = bU_n^{\dagger }(\theta _n) \ldots bU_{i+1}^{\dagger }(\theta _{i+1}) bBU_{i+1}(\theta _{i+1}) \ldots bU_n(\theta _n). \end{aligned}$$

(6)

where, $bB_{i+1}$ represents the new observable obtained after combining gates; $bU_n(\theta _n) \ldots bU_{i+1}(\theta _{i+1})$ denotes a sequence of unitary transformations applied in reverse order; $bU_n^{\dagger }(\theta _n) \ldots bU_{i+1}^{\dagger }(\theta _{i+1})$ represents the adjoint (or conjugate transpose) of the unitary transformations.

This transformation simplifies the case of multiple unitary gates into a single unitary gate, resulting in the quantum function given by:

$$\begin{aligned} f(x; \theta ) = \langle \psi _{i-1} | L_{\theta _i}({\hat{B}}_{i+1}) | \psi _{i-1} \rangle . \end{aligned}$$

(7)

where, $f(x; \theta )$ represents the quantum function; $\psi _{i-1}$ denotes the input state; $L_{\theta _i}({\hat{B}}_{i+1})$ is the quantum operator acting on the input state; $\theta$ represents the parameters of the quantum circuit; ${\hat{B}}_{i+1}$ is the observable associated with the $i+1-th$ unitary transformation.

The gradient is expressed as:

$$\begin{aligned} \nabla _{\theta _i} f(x; \theta ) = \langle \psi _{i-1} | \nabla _{\theta _i} L_{\theta _i}({\hat{B}}_{i+1}) | \psi _{i-1} \rangle . \end{aligned}$$

(8)

$\nabla _{\theta _i} f(x; \theta )$ represents the gradient of the quantum function with respect to the parameter $\theta _i$; $\psi _{i-1}$ denotes the input state; $L_{\theta _i}({\hat{B}}_{i+1})$ is the quantum operator acting on the input state with respect to the parameter $\theta _i$; $\theta$ represents the parameters of the quantum circuit; ${\hat{B}}_{i+1}$ is the observable associated with the $i+1-th$ unitary transformation.

This shows that the gradient optimization of quantum circuits adjusts the parameters of the circuit without modifying its structure.

Consider a common Pauli gate²², which can be represented as:

$$\begin{aligned} bU_i(\theta _i) = \exp \left( -i \frac{\theta _i}{2} {\hat{P}}_i \right) , \end{aligned}$$

(9)

where $\theta _i$ is the unitary gate parameter, and ${\hat{P}}_i$ satisfies ${\hat{P}}_i^{\dagger } = {\hat{P}}_i$. The gradient of $\theta _i$ is given by:

$$\begin{aligned} \nabla _{\theta _i} bU_i(\theta _i) = -i \frac{1}{2} {\hat{P}}_i bU_i(\theta _i) = -i \frac{1}{2} bU_i(\theta _i) {\hat{P}}_i. \end{aligned}$$

(10)

After replacing the equation with Eq. (10) into the expected function $f(x, \theta _i)$, the result is :

$$\begin{aligned} \begin{aligned} \nabla _{\theta _i} f(x; \theta )&= i \frac{1}{2} \langle \psi _{i-1} | bU_i^{\dagger }(\theta _i) \{ {\hat{P}}_i, {\hat{B}}_{i+1} \} bU_i(\theta _i) | \psi _{i-1} \rangle \\&= i \frac{1}{2} \langle \psi _{i-1} | bU_i^{\dagger }(\theta _i) [{\hat{P}}_i, {\hat{B}}_{i+1}] bU_i(\theta _i) | \psi _{i-1} \rangle , \end{aligned} \end{aligned}$$

(11)

Involving the commutation relation, noted as $[\cdot , \cdot ]$, which adheres to $[X, Y] = XY - YX$. When dealing with commutators involving Pauli operators, Eq. (13) can be deduced as follows:

$$\begin{aligned} \begin{aligned} [{\hat{P}}_i, {\hat{B}}_i]&= -i \left[ bU_i^{\dagger }(\theta _i) \frac{\pi }{2} {\hat{B}} bU_i(\theta _i), bU_i^{\dagger }(\theta _i) \frac{-\pi }{2} {\hat{B}} bU_i(\theta _i) \right] \\&= -i \left[ bU_i^{\dagger }(\theta _i) \frac{\pi }{2} {\hat{B}}, bU_i(\theta _i) \right] + i \left[ bU_i^{\dagger }(\theta _i) \frac{-\pi }{2} {\hat{B}}, bU_i(\theta _i) \right] . \end{aligned} \end{aligned}$$

(12)

After substituting Eq. (13) in Eq. (12), the result is Eq. (14):

$$\begin{aligned} \begin{aligned} \nabla _{\theta _i} f(x; \theta )&= \frac{1}{2} \langle \psi _{i-1} | bU_i^{\dagger }(\theta _i + \frac{\pi }{2}) {\hat{B}}_{i+1} bU_i(\theta _i + \frac{\pi }{2}) | \psi _{i-1} \rangle \\&\quad - \frac{1}{2} \langle \psi _{i-1} | bU_i^{\dagger }(\theta _i - \frac{\pi }{2}) {\hat{B}}_{i+1} bU_i(\theta _i - \frac{\pi }{2}) | \psi _{i-1} \rangle . \end{aligned} \end{aligned}$$

(13)

This can be rewritten as a quantum function in Eq. (14):

$$\begin{aligned} \nabla _{\theta } f(x; \theta ) = \frac{1}{2} \left[ f(x; \theta + \frac{\pi }{2}) - f(x; \theta - \frac{\pi }{2}) \right] . \end{aligned}$$

(14)

where, $\nabla _{\theta } f(x; \theta )$ represents the gradient of the quantum function with respect to the parameter $\theta$; $f(x; \theta )$ is the quantum function evaluated at input x with parameters $\theta$; $\theta$ denotes the parameters of the quantum circuit.

Here, the methods of encoding classical information into quantum states are explored, essential for the proposed algorithm’s functionality.

Amplitude encoding involves encoding an N-dimensional classical vector ${\textbf{x}}$ into n qubits, where $n = \lceil \log _2 N \rceil$. The encoded quantum state is given by:

$$\begin{aligned} | {\textbf{x}} \rangle = \sum _{i=1}^{N} x_i | i \rangle , \end{aligned}$$

(15)

here $| i \rangle$ represents a basis in the Hilbert space. The amplitude coding technique ensures that the normalization condition required by quantum mechanics is satisfied, and classical data undergoes normalization before encoding. This method significantly reduces the number of qubits needed to encode classical data.

Classical information can also be encoded into quantum states using rotation gates. The angles of these gates are determined by the classical information ${\textbf{x}}$:

$$\begin{aligned} | {\textbf{x}} \rangle = \bigotimes _{i} {\textbf{S}}(x_i) | 0 \rangle ^n, \end{aligned}$$

(16)

where, $| {\textbf{x}} \rangle$ represents the quantum state encoding classical information; $\bigotimes _{i}$ denotes the tensor product operation over each qubit; ${\textbf{S}}(x_i)$ represents the rotation gate applied to qubit i based on the classical information $x_i$; $| 0 \rangle ^n$ is the initial state of n qubits, typically representing the computational basis state; $x_i$ represents the $i-th$ element of the classical data vector ${\textbf{x}}$.

Here, the number of qubits needed corresponds to the dimensionality of the classical data.

Instantaneous Quantum Polynomial-style (IQP) encoding is another method for encoding classical information. The quantum state is given by:

$$\begin{aligned} | {\textbf{x}} \rangle = \left( {\textbf{U}}_Z({\textbf{x}}) {\textbf{H}}^{\otimes n} \right) ^r | 0^n \rangle , \end{aligned}$$

(17)

where r is the depth of the circuit, and ${\textbf{H}}^{\otimes n}$ performs a Hadamard transform on all qubits. The encoding circuit ${\textbf{U}}_Z({\textbf{x}})$ operates with bRZ gates for each pair of qubits in set S.

In the defined set of three methods, the Angle Encoding is used for the transformation of classical information into quantum states. Additionally, Angle Encoding provides an efficient way to encode classical information without the need to directly share sensitive data, potentially aligning with privacy concerns.

It explains the process of combining classical and quantum information and highlights the encoding of classical data into quantum states using rotation gates and other techniques.

$\beta$-variational quantum eigensolver optimization

In this section an optimization of the algorithm introduced in²³ is presented.

Instead of randomly drawing from the entire set of computational basis states, a selection of the top R states with the highest probabilities is used, controlled by a novel parameter $\alpha$. Subsequently, $p_\phi$ is renormalize based on these selected states, resulting in a $\beta$-Variational Quantum Eigensolver density matrix with a constrained rank of R:

$$\begin{aligned} \rho _{\theta , \phi } = \frac{1}{\sum _{i=1}^{R} p_\phi (s_i)} \sum _{j=1}^{R} p_\phi (s_j) U_\theta |s_j\rangle \langle s_j| U_\theta ^\dagger . \end{aligned}$$

(18)

This adjusted methodology, now incorporating the $\alpha$ parameter, leads to truncated gradients for the variational free energy. The advantage lies in the ability to heuristically choose small values for both R and $\alpha$ to mitigate computational costs during optimization and improve convergence.

The motivation for this optimization lies in enhancing computational efficiency and convergence during the optimization process. The adjustment involves a strategic deviation, introducing a novel parameter, $\alpha$, and focusing on selecting the top states with the highest probabilities, thereby constraining the rank of the density matrix. This modification aims to strike a balance between computational costs and algorithm performance. The incorporation of $\alpha$ facilitates more controlled and efficient optimization, offering a nuanced approach to tailor the algorithm to the specific requirements of the healthcare system model.

After the initial training, local iterations are performed to refine the global parameters of the $\beta$-Variational Quantum Eigensolver. This iterative process optimizes the performance of the $\beta$-Variational Quantum Eigensolver based on the specific characteristics of the patient’s data. The global model is updated iteratively, incorporating insights from each local iteration while preserving data anonymity.

The nested-loop algorithm is performed for training a Quantum Boltzmann Machine (QBM) using a truncated rank $\beta$-Variational Quantum Eigensolver. The objective is to train the QBM to resemble a target dataset embedded in $\eta$. The algorithm initiates with a basic ansatz for the QBM Hamiltonian $H_w$, such as a Heisenberg model or a random spin-glass model.

In the inner loop, the $\beta$-Variational Quantum Eigensolver ansatz $\rho _{\theta ,\phi }$ is trained to represent the QBM $\sigma _w$. In the outer loop, $\rho _{\theta ,\phi }$ is utilized to compute approximate QBM statistics $\text {tr}(H_r\sigma _w) \approx \text {tr}(H_r\rho _{\theta ^*,\phi ^*})$. These statistics are employed to train the QBM through gradient descent.

Given that $H_w$ undergoes slight changes between two QBM iterations, a warm-start strategy is employed for the parameters $\theta , \phi$ of the $\beta$-VQE ansatz $\rho _{\theta ,\phi }$ during the outer loop steps. The converged parameters of $\rho _{\theta ,\phi }$ from one $\beta$-VQE inner loop are reused as the initial parameters for the next inner loop. Consequently, while the $\beta$-VQE may require a relatively long time in the first inner loop, it converges much faster in subsequent iterations.

This optimization for the $\beta$-Variational Quantum Eigensolver selects the top states with the highest probabilities, constrained by a parameter $\alpha$, to improve computational efficiency and convergence in healthcare system models.

Performance evaluation

A synchronous method if the framework is performed, necessitating the server to wait for each participating Quantum client to conclude its local iterations and return their parameters. Only after all Quantum clients have submitted their parameters does the server aggregate them.

Datasets and simulation environment

To conduct our research, an openly available medical dataset was used, as the Fetal Health Datasets²⁴ with 2126 fetal cardiotocograms (CTGs). The dataset comprises measurements of fetal heart rate (FHR) and uterine contraction (UC) features obtained from cardiotocograms, which have been categorized by expert obstetricians. This dataset represents information sourced from the IoMT.

The experiments were performed using a quantum circuit with parameters optimized through federated learning. The dataset was split into training and testing sets, with 80% used for training and 20% for testing. In this wok, the performance of our model was evaluated using standard classification metrics, including accuracy, precision, recall, and F1 score.

The experiments were conducted to predict fetal health using a centralized training approach as well as training with two, four, and eight Quantum Clients. For comparison, tests with a central training was also performed to be compared with the distributed configuration, providing insights into the performance under different distributed computing setups.

For the fetal health prediction experiments, simulations were performed with varying settings to assess the impact of different factors. The experiments involved different numbers of quantum clients, each trained with a learning rate of 0.01, a batch size of 16, and a total of 300 iterations.

Results

The mean accuracy achieved through centralized training and Variational Quantum Neural Network employing $\beta$-QuAFIDA on both the training and testing datasets are presented in Tables 1 and 2.

Table 1 Average Accuracy of $\beta$-QuAFIDA on Fetal Dataset.

Table 2 Average Accuracies with and without Personalized Training.

The experimental results of accuracy of the proposed algorithm are provided in Figure 3. Additionally, is shown the loss function defined in Eq. (1) according to the number of Iterations.

Fig. 3

Train/Test accuracy and respective Loss function for different configurations, in which (a) and (b) represent a central training; (c) and (d) represent the use of two Quantum clientes; (e) and (f) represent four Quantum clients; (g) and (h) represent eight Quantum clients.

The assessment of Noisy Intermediate-Scale Quantum (NISQ) computing holds significant importance in the evaluation of Variational Quantum Neural Networks. Hence, we analyze four distinct types of single-qubit quantum noise: bit flip noise, named of BF, phase flip noise named of PF, amplitude damping noise, AD, and depolarization noise, named of DN. These noises are characterized by their respective Kraus matrix representations $Mk_1$, defined by equations (19) until (22).

$$\begin{aligned} Mk_1&= \sqrt{1 - p}I, \quad Mk_2 = \sqrt{p}\sigma _x, \quad (\text {BF Noise}) \end{aligned}$$

(19)

$$\begin{aligned} Mk_1&= \sqrt{1 - p}I, \quad Mk_2 = \sqrt{p}\sigma _y, \quad (\text {PF Noise}) \end{aligned}$$

(20)

$$\begin{aligned} Mk_1&= \begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1 - p} \end{pmatrix}, \quad Mk_2 = \begin{pmatrix} 0 & \sqrt{p} \\ 0 & 0 \end{pmatrix}, \quad (\text {AD Noise}) \end{aligned}$$

(21)

$$\begin{aligned} Mk_1&= \sqrt{1 - p}I, \quad Mk_2 = \frac{1}{\sqrt{3}}\sigma _x, \quad Mk_3 = \frac{1}{\sqrt{3}}\sigma _y, \quad Mk_4 = \frac{1}{\sqrt{3}}\sigma _z. \quad (\text {DN Noise}) \end{aligned}$$

(22)

where, I, $\sigma _x$, $\sigma _y$, and $\sigma _z$ represents the Pauli matrices. They indicates the robustness of quantum algorithms. The formula for calculating fidelity between two states is given in the following.

$$\begin{aligned} FS(\rho , \sigma ) = \text {B}\left( \sqrt{\rho }\sigma \sqrt{\rho }\right) ^2, \end{aligned}$$

(23)

where $\rho$ and $\sigma$ represent the density matrices of the two mixed states. The fidelity of the quantum circuit is assessed under single noise and a combination of two noises at $p = 0.1$. B represents a Bloch operator, which is used to quantify the distance between two quantum states. The Bloch operator is a function of density operators that acts on the product $\left( \sqrt{\rho }\sigma \sqrt{\rho }\right) ^2$ to calculate the fidelity between the states $\rho$ and $\sigma$.

The results are summarized in Tables 3 and 4. Upon analyzing the obtained results, it is observed that the fidelity of the local circuit decreases under various types of noise. However, it consistently maintains high values, demonstrating good accuracy even in noisy environments.

Table 3 presents the fidelities of the local $\beta$-QuAFIDA under different single-noise scenarios. It is evident that even in the presence of various single noises, such as BF (Brownian noise, PF (Poissonian noise), AD (Amplitude damping noise), and DN (Dephasing noise), the fidelity remains relatively high. These results indicate the robustness of the local $\beta$-QuAFIDA against different types of single noise. Regarding the relation to the Bloch operator, the fidelity values reflect the ability of the quantum system to maintain coherence and preserve information encoded in the quantum states despite the presence of noise.

Table 3 Fidelities of Local $\beta$-QuAFIDA Under Different Single-Noise.

Table 4, on the other hand, illustrates the fidelities of the local $\beta$-QuAFIDA under different mixed noise conditions. Here, mixed noises refer to combinations of two types of noise. Despite the presence of mixed noises like BF and PF, BF and AD, BF and DN, PF and AD, PF and DN, and AD and DN, the fidelity remains relatively high in each case. Again, these results indicate the robustness and adaptability of the local $\beta$-QuAFIDA in handling mixed noise scenarios. In terms of the relation to the Bloch operator, the fidelity values provide insights into how well the quantum states maintain their orientation and coherence in the presence of mixed noise, thus reflecting their ability to effectively utilize the quantum properties encoded in the Bloch sphere representation.

Table 4 Fidelities of Local $\beta$-QuAFIDA Under Different Mixed Noises.

Discussions

In this work was observed that the model’s accuracy remained consistent even in noisy environments, showcasing the robustness of the approach under challenging conditions. Fidelity analyses under various types of noise quantified the performance of the local $\beta$-QuAFIDA algorithm, emphasizing the maintenance of high fidelity levels even in the presence of diverse interference.

Furthermore, the presented figures clearly illustrated the training evolution in terms of accuracy and loss function across iterations. Satisfactory model convergence was observed, indicating the efficacy of the proposed algorithm in the context of fetal diagnosis. The fidelity table under different noise configurations provided a comprehensive view of the resilience of the $\beta$-QuAFIDA model in challenging environments.

These results converge to support the viability and effectiveness of the proposed model, reinforcing its applicability in medical diagnostic scenarios. The discussion also underscored the importance of the FL approach in preserving data privacy, a crucial aspect in health applications.

In summary, the results analysis and interpretations presented in the discussion section emphasize the promising application of the proposed algorithm in the context of fetal diagnosis, providing valuable insights for advancing research in federated quantum machine learning in the healthcare domain.

Conclusions

In conclusion, the developed $\beta$-QuAFIDA algorithm exhibits significant promise for enhancing fetal health prediction within the domain of federated quantum machine learning. The comprehensive evaluation and analysis of the proposed model demonstrated its robustness and effectiveness across various configurations, with a particular emphasis on maintaining accuracy in the presence of quantum noise. The exploration of FL in the quantum domain, specifically tailored for healthcare applications, marks advancements in the field. The integration of classical and quantum computing techniques, as exemplified by the $\beta$-QuAFIDA algorithm, showcases the potential for efficient and privacy-preserving medical diagnostic models. The potential privacy and security challenges associated with federated learning using quantum computing in healthcare include protecting sensitive patient data during training and transmitting learning models between quantum clients. The proposed framework addresses these challenges through the federated learning technique, which allows data to remain localized on client devices while only updated learning models are shared between them. This helps mitigate privacy and security risks by ensuring that sensitive patient data is not exposed to unauthorized third parties. The study’s utilization of the Fetal Health Dataset in combination with federated quantum learning contributes with insights into the model’s performance under different distributed computing setups. The experimentation with varying numbers of Quantum clients underscored the adaptability and scalability of the proposed algorithm. Moreover, the fidelity analyses provided a quantitative measure of the algorithm’s resilience to different types of noise, crucial for real-world applications where noise is an inherent challenge. The consistently high fidelity levels, even in the presence of noise, reinforce the algorithm’s suitability for deployment in practical healthcare scenarios. The iterative training process, coupled with personalized training approaches, further refines the global parameters of the Variational Quantum Eigensolver, highlighting the adaptability of the model to specific patient data characteristics. The beta-Variational Quantum Eigensolver Optimization contributes to improving the efficiency and convergence of the algorithm by selecting the most relevant states with the highest probabilities, limited by a parameter $\alpha$, to enhance computational efficiency and convergence in healthcare system models. This optimization allows for choosing heuristic small values for both R and $\alpha$ to mitigate computational costs during optimization and improve convergence. However, one potential limitation to consider is the sensitivity of the algorithm’s performance to the choice of these parameters. While heuristic selection can mitigate this to some extent, the optimization process may still require careful parameter tuning. In light of these findings, the $\beta$-QuAFIDA algorithm not only demonstrates a good performance in predictive accuracy but also aligns with privacy concerns through its FL approach. The presented results lay a foundation for future research and development in federated quantum machine learning for healthcare, paving the way for innovative applications in intelligent diagnosis within 5G mobile networks. It demonstrates robustness and effectiveness across various configurations, maintaining accuracy even in the presence of quantum noise, and highlights the potential for efficient and privacy-preserving medical diagnostic models through its integration of classical and quantum computing techniques. In future work, we intend to compare the performance of the proposed framework with other machine learning methods in fetal health, as well as to evaluate the impact of different parameter settings on algorithm performance. Additionally, we plan to test it on other healthcare datasets to evaluate its scalability. As the healthcare industry increasingly integrates quantum technologies, the proposed algorithm’s potential impact on personalized and efficient medical diagnostics remains a compelling avenue for further exploration and refinement. The successful convergence of classical and quantum computing in the $\beta$-QuAFIDA model positions it as a noteworthy contribution to the evolving landscape of quantum-assisted healthcare solutions.