Introduction

Purification of pharmaceutical compounds is of great importance for pharmaceutical manufacturing which can be conducted by different separation techniques such as crystallization, membranes, distillation, etc. Use of the proper separation method can help enhance process efficiency in such as way to maximize the overall manufacturing efficiency. Currently, crystallization is performed as the primary use for separation of organic compounds from reaction process1,2,3,4. The process is based on solid–liquid separation which produces the output as slurry followed by isolation of products. Crystals with different forms/habits and sizes can be formed in crystallization if the process is not well controlled. Other separation methods such as membranes can be also used for separation of pharmaceutical compounds from solutions. Membrane systems can operate by utilization of membrane contactors which are porous membranes for contacting two phases.

One of the methods applied for crystallization is membrane distillation which can be grouped as hybrid process due to combination of membrane and distillation for crystallization5,6,7. Membrane distillation (MD) is operated in membrane contactor devices for separation of target molecules. The driving force of the process can determine the type of membrane distillation including direct-contact operation, vacuum operation, etc. In vacuum membrane distillation (VMD), the compounds are separated by creation of vacuum across the membrane and then diffusion of target compound through the membrane pores. Hollow-fiber membrane contactors are usually used for vacuum membrane distillation due to their great properties in separation8,9.

For development of VMD process in pharmaceutical separation, computational techniques can be used to understand the process and optimize it. Various methods can be applied such as mechanistic models and machine learning models. Basically, heat and mass transfer models are applied for analysis of membrane distillation. The governing equations pertaining to heat/mass transfer can be solved via Computational Fluid Dynamics (CFD) methods10,11,12. Once the equations have been solved, concentration and temperature distributions in the membrane can be obtained for interpretation of the process and separation efficiency. Due to the complexity of CFD in membrane simulations, models based on data-driven techniques should be employed for some industrial applications as these models are easier to run and optimize. Machine learning models are the preferred ones to simulate membrane distillation, however these models can be combined with CFD to correlate mass transfer dataset. This approach has been successfully applied to MD process with promising results13 which opens new horizon for expanding this methodology. However, other machine learning models should be tested for VMD process to make a generalized hybrid modeling.

The wide term of Machine Learning (ML) refers to a group of methods allowing computers to learn from data without explicit programming. Developing meta-programs enables ML to evaluate experimental data and apply it to train models for future predictions14,15. In this research, the Bagging Ensemble technique was applied on several models comprising k-nearest neighbors (KNN), polynomial regression (PR), and Tweedie regression (TWR):

  1. 1.

    Polynomial regression (PR) Uses polynomial equations to model the relationship between input parameters and the target variable. Effective for capturing non-linear trends in data.

  2. 2.

    K-Nearest neighbors (KNN) Predicts the output by averaging the values of the k closest data points in the feature space. Suitable for both linear and non-linear relationships.

  3. 3.

    Tweedie regression (TWR) This algorithm is a generalized linear model appropriate for non-negative, right-skewed data with a mass probability at zero. Useful for modeling data with both continuous and discrete characteristics.

In our investigation, using the Bagging ensemble technique—which combines predictions from several models to increase accuracy and lower variance—improved the models. Hyper-parameter optimization was done using the Multi-Verse Optimizer (MVO), which enhanced search and optimization efficiency by means of cosmological events. The models for simulating membrane process in this study have been chosen due to their robustness and flexibility in finding complex relationship between non-linear variables which is not easy to obtain via other modeling techniques.

This paper contributes significantly to the field of predictive modeling by demonstrating the effectiveness of combining single regression models with ensemble techniques and advanced optimization algorithms for estimation of pharmaceutical concentrations in a VMD process. Mass transfer equations are solvent by CFD, and the calculated concentration data are then used for ML correlations in the domain of process. The study shows that prediction accuracy and consistency can be greatly improved by using Polynomial Regression (PR), K-Nearest Neighbors (KNN), and Tweedie Regression (TWR) models, and enhancing them with the Bagging ensemble method. The novelty is related to tuning hyperparameters using the Multi-Verse Optimizer (MVO), and combination of mass transfer with several ML models to simulate pharmaceutical purification by vacuum membrane distillation process.

Process description

The process under investigation is a vacuum membrane distillation which is operated using hollow-fiber configuration. The process is used to separate a pharmaceutical compound from a solution by the creation of vacuum across the membrane. Mass transfer mechanisms of solute including molecular diffusion and convection were taken into account for building the model. CFD was used for the feed and membrane sides of process to obtain concentration distribution, and the data was used for machine learning. The CFD simulations were carried out in COMSOL Multiphysics package (v. 3.5a) via finite element technique (UMFPACK solver)16. The methodology has been followed from the previous work13. For mass transfer of drug in the process, convection–diffusion model was expressed as follows17,18:

$${{N}_{drug}=-D}_{drug}\nabla {C}_{drug}+{V}_{Z}{C}_{drug}$$
(1)

Inside the membrane, only diffusional mass transfer was considered as follows13:

$${D}_{drug,M}\left[\frac{{\partial }^{2}{C}_{drug,M}}{\partial {r}^{2}}+\frac{{\partial }^{2}{C}_{drug,M}}{\partial {z}^{2}}\right]=0$$
(2)

where M refers to membrane phase and D is the drug diffusivity inside the membrane. C is the drug concentration which is a function of r and z (coordinates). At the inlet of membrane module, a fixed concentration boundary condition was assumed, while convective flow was considered for the outlet boundary. Also, thermodynamic equilibrium was assumed as boundary condition for the interface between feed and membrane. The data from each node was extracted for ML modeling. The meshed geometry of the domain is illustrated in Fig. 1. The data utilized for ML modeling has three variables: r, z, and C. Data analytics performed in this study was conducted using Python programming language (3.8 version).

Fig. 1
figure 1

Geometry of the VMD meshed for CFD simulations.

Full size image

Figure 2 displays a correlation heatmap that illustrates the connections across variables. The color intensity signifies the magnitude of the correlation, with negative correlations depicted in varying degrees of blue and positive correlations represented in varying shades of red. Furthermore, Fig. 3 displays the histograms that illustrate the frequency distribution of the variable. Every histogram is accompanied with a density plot overlay, which allows for visualizing the shape of the distribution and detecting any skewness in the data.

Fig. 2
figure 2

Correlation heatmap showing the relationships between r(m), z(m), and C(mol/m3).

Full size image
Fig. 3
figure 3

Histograms depicting the frequency distribution of r, z, and Concentration (C).

Full size image

To ensure the robustness and reliability of the dataset, Isolation Forest was employed for outlier detection. Isolation Forest is an unsupervised learning algorithm that excels at anomaly detection tasks19,20. The method constructs a collection of trees (forest) in which the paths leading to the identification of anomalies have shorter lengths. A decision function is constructed by calculating the average path length from the forest, which efficiently identifies outliers. Utilizing this approach facilitates the detection and elimination of anomalies, hence improving the caliber and dependability of the subsequent analysis and modeling19.

Methods

Multi-verse optimizer (MVO)

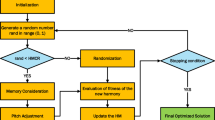
MVO, short for Multi-Verse Optimizer, draws inspiration from three cosmological phenomena: white holes, black holes, and wormholes. This algorithm applies the concepts of black holes and white holes for search space exploration, with wormholes utilized to exploit these spaces. Initially, a collection of random universes is created21,22. During each iteration, entities from high-inflation universes have a tendency to shift to low-inflation universes through white and black holes. Simultaneously, random teleportations occur towards the optimal universe through wormholes. The algorithm computes two parameters to control the extent and frequency of solution alterations22:

$$\text{Probability of Wormhole Existence (PWE)}=a+t\left(\frac{b-a}{T}\right)$$
(3)
$$\text{Rate of Travelling Distance (RTD)}=1-{t}^{1/p}\left(\frac{1}{{T}^{1/p}}\right)$$
(4)

where a refers to the minimum value, b denotes the maximum value, t indicates the current iteration, T stands for the total number of iterations, and p defines the accuracy of exploitation. The updated positions of solutions are derived by subtracting the computed values of PWE and RTD into the following equation22:

$${x}_{ji}= \left\{\begin{array}{c}{x}_{j}+RTD+\left(\left({u}_{j}-{l}_{j}\right)\cdot {r}_{4}+{l}_{j}\right) {r}_{3}<0.5\\ {x}_{j}-RTD+\left(\left({u}_{j}-{l}_{j}\right)\cdot {r}_{4}+{l}_{j}\right) {r}_{3}\ge 0.5\end{array}\right.$$
$${x}_{ji}={x}_{j}^{{\text{Ro}}\text{ulette Wheel}}\hspace{1em}\text{if }{r}_{2}\ge PWE$$

where \({x}_{j}\) represents the j-th element of the best solution, \({l}_{j}\) and \({u}_{j}\) are the lower and upper bounds of the j-th element, respectively. Moreover, \({r}_{2}\), \({r}_{3}\), \({r}_{4}\) denote random numbers sampled from the range [0, 1], \({x}_{ji}\) denotes the j-th parameter in the i-th solution, and \({x}_{j}^{Roulette wheel}\) is the j-th element of a solution selected using the roulette wheel selection method. The algorithm facilitates exploration and exploitation by varying \({r}_{2}\), \({r}_{3}\), and \({r}_{4}\). Initially, a set of random solutions is generated, and their respective objectives are computed. The positions of the solutions are then updated using the above equations. This process is repeated until a termination criterion is met.

Bagging ensemble model

Bootstrap Aggregation, commonly referred to as bagging, stands as a widely utilized ensemble technique. Bagging Regression culminates in the final prediction by aggregating the predictions of individual models derived from a randomized selection of the original data through averaging (for regression) or voting (for classification). This meta-estimator is proficient in substantially diminishing the variance it produces by incorporating a randomization mechanism in its prediction formulation. Furthermore, this approach proves beneficial in mitigating overfitting concerns associated with complex algorithms. Boosting regressions, on the other hand, yield more precise results through the utilization of weak (base) models23,24. Figure 4 illustrates the comprehensive architecture of the bagging process.

Fig. 4
figure 4

Bagging process.

Full size image
Fig. 5
figure 5

Predicted and reference concentration values using BAG-KNN model.

Full size image
Fig. 6
figure 6

Predicted and reference concentration values using BAG-PR model.

Full size image
Fig. 7
figure 7

Predicted and reference concentration values using BAG-TWR model.

Full size image

Polynomial regression (PR)

Polynomial regression (PR) is beneficial when there is evidence to suggest that the relationship between two variables is not linear, but instead follows a curved pattern. This approach represents the correlation between output parameter and multiple input parameters by employing a polynomial model25,26. Considering the dependent parameter as y and an independent parameter x, the equation for polynomial regression is given by27:

$$y={a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}+\dots +{a}_{n}{x}^{n}$$
(5)

Here, x denotes the independent variable, y stands for the dependent variable, \({a}_{0},{a}_{1},{a}_{2},\dots ,{a}_{n}\) are the coefficients, and n stands for the polynomial's degree. The degree of the polynomial controls the form of the curve most suitable for the data.

K-nearest neighbors (KNN)

KNN regression works by determining the k closest neighbors to a new unseen data point within the feature space. Following this step, the model predicts the output by calculating the average or weighted average of the output values derived from those k neighbors. The algorithm can be summarized in the following steps28:

  1. 1.

    Using a distance metric, estimate how far the new data is from the rest of the training set:

    $$d\left({x}_{i},{x}_{j}\right)=\sqrt{{\sum }_{k=1}^{n}{\left({x}_{ik}-{x}_{jk}\right)}^{2}}$$
    (6)

    where \({x}_{i}\) and \({x}_{j}\) are two data points in the feature space, n denoted the count of features, and \({x}_{ik}\) and \({x}_{jk}\) are the values of k-th feature for i–th and j-th data points.

  2. 2.

    Choose the k-nearest neighbors by considering the calculated distances.

  3. 3.

    Take the mean or weighted average of the outputs of the KNN to arrive at the output value for the new data point:

    $$\widehat{y}=\frac{{\sum }_{i=1}^{k}{w}_{i}{y}_{i}}{{\sum }_{i=1}^{k}{w}_{i}}$$
    (7)

    Here, \(\widehat{y}\) stands for the predicted output value, \({y}_{i}\) is the output value of the i-th nearest neighbor, and \({w}_{i}\) stands for the weight of the i-th closest neighbor. The weights can be assigned according to the inverse of the distance to the new data point.

KNN regression has several advantages over other regression algorithms. It is effective for handling linear and non-linear connections between input features and the target variable, and it can be implemented quickly29,30.

Tweedie regression (TWR)

The Tweedie regression model is a specific form of Generalized Linear Model (GLM) that is particularly suitable for analyzing data that is non-negative, significantly right-skewed, and exhibits both symmetric and heavy-tailed characteristics. It is particularly useful for continuous data that may have a probability mass at zero31. A random variable Y is considered to follow a Tweedie distribution if its density function is a member of the class of exponential dispersion models (EDM). The density function can be represented by the following expression32:

$${f}_{Y}\left(y;\upmu ,\upphi ,p\right)=a\left(y,\upphi ,p\right)\text{exp}\left\{\frac{y\uppsi -k\left(\uppsi \right)}{\upphi }\right\}$$
(8)

where \(\upmu =E\left(Y\right)={k}{\prime}\left(\uppsi \right)\) denotes the mean, \(\upphi > 0\) signifies the dispersion parameter, \(\uppsi\) represents the canonical parameter, and \(k\left(\uppsi \right)\) corresponds to the cumulant function. Here is the formula for the variance of Y32:

$${\text{Var}}\left(Y\right)=\upphi V\left(\upmu \right)=\upphi {\upmu }^{p}$$
(9)

Here, p is the power parameter, which determines the form of the variance function and thus the specific distribution within the Tweedie family. Tweedie regression models are extensively used in various fields, including insurance (for modeling claims data), biology, ecology, and econometrics. The flexibility of the Tweedie distribution makes it an excellent choice for modeling data that exhibit both continuous and discrete characteristics, such as insurance claims that have a large number of zeros and positive continuous values. Estimation of the parameters in Tweedie regression models can be challenging due to the complex form of the density function. The paper discusses two alternative estimation methods: quasi-likelihood and pseudo-likelihood. These methods are computationally simpler and faster than the traditional maximum likelihood estimation, especially when the power parameter p falls within complex ranges.

Results and discussion

The results shown in Tables 1 and 2 indicate that the ensemble models (bagging on the top of KNN, PR, and TWR) performed well, with varying degrees of accuracy and precision. The BAG-KNN model achieved the highest R2 score for both training (0.99918) and testing (0.99923) datasets, indicating a very high level of accuracy in predicting the output variable C based on the inputs r and z. The K-fold cross-validation also showed a high mean R2 score (0.99776) with low standard deviation (0.00151), signifying consistent performance across different subsets of the data. Additionally, this model had the MSE and MAE, as well as the smallest Average Absolute Relative Deviation (AARD%), which underscores its robustness and reliability in predicting C.

Table 1 R2 scores with Cross Validation results.
Full size table
Table 2 Performance evaluation of the optimized models.
Full size table

The Polynomial Regression model with Bagging also performed well, though not as exceptionally as the KNN model. The R2 scores for the training (0.99668) and testing (0.99741) datasets were slightly lower but still indicative of strong predictive power. The K-fold mean R2 score (0.99650) and low standard deviation (0.00081) further support the model's reliability. However, the MSE, MAE, and AARD% values were higher compared to BAG_KNN, indicating that while the model performs well overall, there is a slightly larger margin of error in the predictions.

The Tweedie Regression model with bagging had the lowest R2 scores among the three models for both training (0.95747) and testing (0.96044) datasets, suggesting a comparatively lower accuracy. The K-fold cross-validation results also showed a higher standard deviation (0.00736), implying less consistency in performance. Additionally, the MSE, MAE, and AARD% were significantly higher than those of the other two models, indicating that the BAG-TWR model had more considerable errors and deviations in its predictions. Figures 5, 6, and 7 are a comparison of predicted and experimental Concentration values using three models.

Finally, the BAG-KNN model emerges as the most precise and dependable in forecasting C based on the inputs r and z. The Learning Curve of this model is displayed in Fig. 8. The better performance of the system is clearly demonstrated by its greatest R2 scores, lowest error metrics, and consistent performance across several data subsets. The BAG-PR model, albeit significantly less exact, nonetheless exhibits robust predictive abilities, rendering it a feasible choice. Nevertheless, the BAG-TWR model exhibits a significant decrease in performance and consistency, rendering it the least efficient of the three assessed models. Hence, after doing a thorough examination of the R2 scores, error metrics, and consistency, it can be concluded that the BAG-KNN model is the optimal selection for this dataset and prediction task. Figures 9 and 10 show the individual effects of the inputs on concentration by means of BAG-KNN model. Furthermore, Fig. 11 depicts the correlation between concentration and the variables r(m) and z(m). The change of drug concentration in the feed channel is clearly calculated by ML models and agree with CFD results. In this VMD process, mass transfer plays crucial role in separating drug molecules from the solution. Both convection and diffusion terms have been taken into account for modeling the VMD process via CFD. The main contribution of convection is in the axial direction where the fluid flows and the velocity of fluid is dominant, while diffusion is significant in radial direction inside the feed channel of VMD33,34.

Fig. 8
figure 8

Learning curve of BAG-KNN.

Full size image
Fig. 9
figure 9

Concentration profile of drug in the feed channel at radial direction.

Full size image
Fig. 10
figure 10

Concentration profile of drug in the feed channel at axial direction.

Full size image
Fig. 11
figure 11

Concentration of drug in the feed side as a function of r and z.

Full size image

Conclusion

The effectiveness of several ensemble regression methods was assessed to predict the concentration of drug in a VMD process as a function of input features r(m) and z(m). The data was obtained on each node of domain (membrane contactor) from a CFD simulation of mass transfer considering both diffusion and convection. The dataset, which included over 3400 data points, was processed to ensure quality and robustness, with the Isolation Forest algorithm used for outlier detection. Polynomial Regression (PR), K-nearest Neighbors (KNN), and Tweedie Regression (TWR) models were boosted with Bagging and found that the Bagging-KNN model outperformed the others. Indicating its better accuracy and dependability for this prediction task, this model displayed the highest R2 scores and the lowest error measures over both training and testing datasets. Although with a somewhat higher error margin, the Bagging-PR model proved to have great predictive power, thus it is a reasonable substitute. The least efficient of the three models assessed, the Bagging-TWR model displayed rather less accuracy and consistency even if it was still useful. Ensemble techniques and advanced optimization algorithms like the Multi-Verse Optimizer (MVO) can improve machine learning models' predictive performance, according to the study. Its excellent performance suggests that the Bagging-KNN model is best for predicting concentration C given inputs. Future research could use other ensemble methods and optimization techniques to improve predictive model accuracy and robustness in similar datasets.