Interval-valued picture fuzzy decision-making framework with partitioned maclaurin symmetric mean aggregation operators

Abstract

Interval-valued picture fuzzy (IVPF) set is an extension of the picture fuzzy set theory used to represent uncertainty and vagueness in the processes of decision-making. This study focuses on exploring the interrelationships among multiple IVPFSs and criteria partitions. We investigate the IVPF partitioned Maclaurin symmetric mean operator and the weighted IVPF partitioned Maclaurin symmetric mean operator and discuss their respective properties. Subsequently, we identify certain special cases of these operators based on IVPF sets. Furthermore, we deploy a multi-criteria decision-making procedure utilizing the suggested IVPF partition operators. Through a numerical example, we demonstrate the practicality and validity of the presented approach. Finally, a thorough comparison with existing approaches is conducted to elucidate the superiority of the proposed method.

Introduction

Decision-making (DM) is an effective contrivance for handling complex and Ambiguous data encountered in everyday scenarios. Multi-criteria decision-making (MCDM) has gained significant attention from various scholars in recent years^1,2,3,4. MCDM is a valuable process utilized in everyday situations to prioritize a limited set of DM issues based on their relevance to the decision-maker. The concept of fuzzy sets (FSs), introduced by Zadeh⁵, incorporates the grade of truth within the unit interval. The FS garnered increasing attention since its inception^6,7. Zadeh later extended this theory to interval-valued fuzzy sets (IVFS)⁸, where the degree of truth is expressed as a restricted subset of the unit interval. Both FS and IVFS have garnered considerable interest and have been utilized across diverse research fields. However, challenges arose when individuals encountered information involving the degree of falsity, a scenario not effectively addressed by the theory of FSs. To address these challenges, Atanassov introduced the idea of intuitionistic FS (IFS)⁹. IFS is an adapted version of FS designed to handle complex information in real DM situations. It incorporates both the degree of accuracy and falsehood, with the constraint that the total must not surpass the unit interval. Additionally, Atanassov¹⁰ expanded on the IFS concept to formulate the concept of interval-valued intuitionistic FS (IVIFS). This extension includes the degree of accuracy and falsehood as a finite subset of the unit interval, with the restriction that the combined upper limits of the degree of accuracy and falsehood must not surpass the unit interval. The ideas of IFS and IVIFS have gained significant concentration from various researchers, and numerous researchers have employed these ideas in diverse fields^11,12,13.

However, the concept of intuitionistic FS (IFS) faced challenges when dealing with information involving degrees of accuracy, abstinence, and falsehood, especially in scenarios like human opinions with responses such as yes, abstinence, no, and refusal. To address these challenges, Cuong introduced the picture FS (PFS)¹⁴. PFS, a modified version of IFS, is designed to handle complex information in real DM issues, such as voting scenarios where individuals may vote in favour, abstain, vote against, or refuse to vote. PFS includes degrees of accuracy, abstinence, and falsehood, with the constraint that their sum cannot surpass the unit interval. Furthermore, Cuong¹⁵ extended the PFS concept to develop the theory of interval-valued picture fuzzy (IVPF) set (IVPFS), incorporating degrees of accuracy, abstinence, and falsehood as a closed subset of the unit interval. The IVPFS constraints ensure that the total of the upper bounds for the degrees of accuracy and falsehood must not surpass the unit interval. IVPFS provides decision-makers with more flexibility, expressing accuracy, abstinence, and falsehood degrees as subintervals of the unit interval instead of crisp sets. The concepts of PFS and IVPFS have garnered concentration from scholars, with researchers applying these concepts to address challenges in various areas^16,17. Khalil et al.¹⁸ highlighted the limitations of the existing operational laws of IVPFSs and proposed an enhanced version with its distinctive features. Ashraf et al.¹⁹ examined Maclaurin symmetric mean (MSM) operators within the context of IVPFS and explored their application in selecting the optimal company benefit plan. In the referenced study²⁰, the authors presented a novel entropy weighting method utilizing IVPFS for calculating the weights of both criteria and sub-criteria. Liu et al.²¹ effectively tackled issues related to mineral field recognition and MCDM by leveraging their developed innovative similarity measures.

Aggregation operators (AOs) are widely utilized tools that amalgamate individual input arguments into a singular argument. Numerous studies have been conducted within the framework of IVPFSs to explore the application and effectiveness of these operators. Ma et al.²⁰ presented the ordered weighted interactive averaging operator and an entropy weighting method grounded in IVPFS. Kamaci et al.²² devised an approach to address multi-period DM problems involving interval-valued picture hesitant fuzzy data, utilizing Einstein operations-based AOs. The authors in^23,24 expanded upon the fundamental IVPF AOs using the frank t-norm and elucidated on the corresponding results. In these AOs, the criteria are considered independently. Nevertheless, in DM problems, the interrelation among criteria cannot be overlooked. Addressing this concern, Kishorekumar et al.²⁵ introduced the IVPF Bonferroni mean (BM) operator. To substantiate the practicality of their proposed AO, a real-world example involving coconut tree yield (CTY) was addressed. Several geometric weighted Heronian mean (HM) operators under the IVPF setting were investigated in²⁶. Moreover, an MCDM algorithm was constructed with the aid of these operators in conjunction with the best-worst method. The Maclaurin symmetric mean (MSM), initially introduced by Maclaurin²⁷, stands out as a widely employed operator featuring an aggregation function. This operator possesses the capability to discern relationships among multiple input arguments. Subsequently, it garnered further attention and extension by Ashraf et al.¹⁹, as the BM²⁵ and HM²⁶ were found to be constrained in capturing relationships only between two input arguments. Moreover, due to the diverse nature of criteria properties in the MCDM problem, it is possible to categorize criteria into distinct groups. Criteria within the same category exhibit interdependence, while those in different categories are considered independent. To illustrate, when choosing a laptop from various options, one may consider four criteria: basic requirements ($\ddagger _1$), customer comments ($\ddagger _2$), price comparison ($\ddagger _3$), and appearance characteristics ($\ddagger _4$). These criteria can be partitioned into two sets: $P_1 = \left\{ \ddagger _1, \ddagger _4\right\}$ and $P_2 = \left\{ \ddagger _2, \ddagger _3\right\}$. It becomes evident that criteria $\ddagger _1$ is interconnected with $\ddagger _4$ within the same partition ($P_1$), as is the case for $\ddagger _2$ and $\ddagger _3$ within partition $P_2$. However, there is no interrelationship between partitions $P_1$ and $P_2$. Therefore, with respect to the categorization of criteria, certain investigations have introduced the partitioned BM (PBM) operator²⁸, partitioned HM (PHM) operator²⁹, and partitioned MSM (PMSM) operator³⁰. However, the developed AOs on IVPFS neglect the segmentation of criteria, rendering them ineffective in addressing DM problems that involve partitioned criteria.

Motivations

Here, we present a thorough analysis of the factors driving this study.

• i) In general, many existing operators^20,22,23,24, developed within the IVPF environment, operate under the assumption that all criteria in MCDM are homogeneous. However, criteria can be both homogeneous and heterogeneous; they may be grouped into distinct categories within a single MCDM problem. Criteria within the same category are interdependent, while those in separate categories are independent. The restriction to considering all criteria within the same category limits the operators’ effectiveness in accurately addressing MCDM problems. Consequently, there is a need for more adaptable operators that enable the MCDM technique to accommodate scenarios with heterogeneous criteria.

• ii) Meanwhile, existing operators^30,31,32 based on the partitioning criteria approach are developed within frameworks such as IFs, PFSs, or bipolar FSs. However, these frameworks may not always accommodate all types of uncertain information. As a result, these approaches might not accurately formulate outcomes in certain scenarios.

• iii) Simultaneously, existing IVPF operators^25,26 lack the capability to take into account the correlation among multiple arguments when making decisions. This limitation means that these operators cannot effectively reflect how changes in one argument may affect others, leading to challenges in accurately estimating outcomes. This deficiency highlights the need for advanced AOs that can seamlessly incorporate correlation considerations and deliver more precise decision outcomes.

Contributions

Building upon the earlier discussion, the pivotal contributions of the current study are included as follows:

• i) To investigate the IVPF PMSM operator and its weighted form, aimed at capturing the intricate interrelationships among multiple criteria, is the primary focus of our study.

• ii) To investigate distinct characteristics, specifically idempotency, monotonicity, and boundedness, alongside theorems and notable instances of the proposed operators, is also the overarching objective of our exploration

• iii) To delineate the stepwise procedure of the innovative MCDM method rooted in the proposed IVPF partition AOs and the associated theoretical framework

• iv) To clarify the practicality and superiority of the initiated MCDM approach, in-depth analysis will be conducted with existing methods using an illustrative MCDM example.

The geometrical representation of the proposed work is depicted in Fig. 1.

Fig. 1

Geometrical representation of the proposed work.

Organization

The rest of the article is managed as follows: In Sec."Some basic concepts", fundamental concepts related to IVPFS, along with other essential notions, are reviewed. Sec."Proposed MSM operators" presents the IVPF PMSM and its weighted counterpart, along with associated findings, supported by their respective proofs. A novel DM methodology founded on these AOs is presented in Sec."Proposed decision-making methodology". In Sec. "Illustrative example", a case study on enterprise resource management selection is undertaken to demonstrate the practical application of the outlined approach. Sec. "Comparative study" provides an illustrative example to demonstrate the utility and validity of the proposed MCDM method. The concluding Sec. "Conclusions" summarizes the contents discussed throughout this paper.

Some basic concepts

Throughout this segment, we allocate some basic ideas related to the picture fuzzy set, IVPF set and PMSM.

Definition³³ 

Consider S as the domain of discourse. Then, a PFS $\mathcal {I}$ on S is defined as:

$$\begin{aligned} \mathcal {I}=\left\{ \left( s, \mathfrak {m}\left( s\right) ,\mathfrak {u}\left( s\right) ,\mathfrak {n}\left( s\right) \right) | s \in S \right\} , \end{aligned}$$

(1)

where $\mathfrak {m}\left( s\right) ,\mathfrak {u}\left( s\right) ,\mathfrak {n}\left( s\right)$ are the functions taking values in the unit interval $\left[ 0,1 \right]$ which represent the membership degree, neutral degree and non-membership degree of $s \in S$ in $\mathcal {I}$ respectively, with given conditions:

$$\begin{aligned} 0\le \mathfrak {m}\left( s\right) + \mathfrak {u}\left( s\right) +\mathfrak {n}\left( s\right) \le 1, \end{aligned}$$

where $\mathfrak {m}\left( s\right)$, $\mathfrak {u}\left( s\right)$ and $\mathfrak {n}\left( s\right)$ represent the membership, neutral part and non-membership degree respectively taking values within the range of [0, 1] for every s in the set S. For convenience, $\mathcal {G}= (\mathfrak {m}\left( s\right) ,\mathfrak {u}\left( s\right) ,\mathfrak {n}\left( s\right) )$ is known as a picture fuzzy element (PFE).

Definition 2³³

Let $\mathcal {I}_{i}$= $\left\{ \mathfrak {m}_{i},\mathfrak {u}_{i},\mathfrak {n}_{i}\right\}$ be the PFE, the score function and the accuracy function are defined as:

$$\begin{aligned} & Sc(\mathcal {I}) = \mathfrak {m}_{i}-\mathfrak {u}_{i}-\mathfrak {n}_{i} \in [-1,1], \end{aligned}$$

(2)

$$\begin{aligned} & Ac(\mathcal {I}) = \mathfrak {m}_{i}+\mathfrak {u}_{i}+\mathfrak {n}_{i} \in [0,1]. \end{aligned}$$

(3)

Definition 3²⁰

Let N be the universal set. Then an IVPFS $\mathfrak {K}$ on N is described as follows:

$$\begin{aligned} \mathfrak {K}= \left\{ <n,\alpha (n),\beta (n),\gamma (n)>;n\in N\right\} . \end{aligned}$$

(4)

here $\alpha$, $\beta$, and $\gamma$ correspondingly represent the positive membership function, neutral membership function, and non-membership function of the set $\mathfrak {K}$. Each of these functions, when applied to N, yields a subset of the interval [0,1]. For every n$\in$N, $\alpha (n),\beta (n),\gamma (n)$ these sets represent certain closed subintervals of [0,1]. Indicating the potential levels of positive membership, neutral membership, and negative membership for n$\in$N with respect to the set $\mathfrak {K}$, respectively. Where $\alpha (n)$= $\left\{ \mathfrak {a}: [\mathfrak {a}^{-},\mathfrak {a}^{+}]\right\}$, $\beta (n)$= $\left\{ \mathfrak {b}: [\mathfrak {b}^{-},\mathfrak {b}^{+}]\right\}$ and $\gamma (n)$= $\left\{ \mathfrak {c}: [\mathfrak {c}^{-},\mathfrak {c}^{+}]\right\}$, under the condition $0\le \mathfrak {a}^{+} + \mathfrak {b}^{+} + \mathfrak {c}^{+} \le$ 1.

For the sake of simplicity, the $\mathcal {G}(n)$=$\left( \alpha (n),\beta (n),\gamma (n)\right)$ is called IVPFE, given by

$$\begin{aligned} \mathcal {G}=\left( \alpha ,\beta ,\gamma \right) = \left( \begin{array}{c} [\mathfrak {a}^{-},\mathfrak {a}^{+}], [\mathfrak {b}^{-},\mathfrak {b}^{+}], [\mathfrak {c}^{-},\mathfrak {c}^{+}] \end{array}\right) . \end{aligned}$$

(5)

Definition 4²⁰

Let $\mathcal {G}$ be the IVPFE. The quantities of values in $\alpha$, $\beta$, and $\gamma$ are $\textsf{h}(\alpha )$, $\textsf{h}(\beta )$, $\textsf{h}(\gamma )$, respectively. Then the score function and the accuracy function will be,

1). Score Function

$$\begin{aligned} Sc(\mathcal {G})=\dfrac{\left( \mathfrak {a}^{-}\right) -(\mathfrak {b}^{-})-(\mathfrak {c}^{-})+\left( \mathfrak {a}^{+}\right) -(\mathfrak {b}^{+})-(\mathfrak {c}^{+})}{2} \in [-1,1], \end{aligned}$$

(6)

2). Accuracy Function

$$\begin{aligned} Ac(\mathcal {G})=\dfrac{\left( \mathfrak {a}^{-}\right) +(\mathfrak {b}^{-})+(\mathfrak {c}^{-})+\left( \mathfrak {a}^{+} \right) +(\mathfrak {b}^{+})+(\mathfrak {c}^{+})}{2} \in [0,1]. \end{aligned}$$

(7)

Definition 5²⁰

Let $\mathcal {G}_{1}$=$\left( \alpha _{1},\beta _{1},\gamma _{1}\right)$ and $\mathcal {G}_{2}$=$\left( \alpha _{2},\beta _{2},\gamma _{2}\right)$ be the two IVPFEs, then we can compare these based on score and accuracy functions as follows:

• 1. if $\mathcal {G}_{1}$ < $\mathcal {G}_{2}$ then $Sc(\mathcal {G}_{1})$ < $Sc(\mathcal {G}_{2})$,

• 2. if $\mathcal {G}_{1}$ > $\mathcal {G}_{2}$ then $Sc(\mathcal {G}_{1})$ > $Sc(\mathcal {G}_{2})$,

• 3. if $\mathcal {G}_{1}$ = $\mathcal {G}_{2}$ then $Sc(\mathcal {G}_{1})$ = $Sc(\mathcal {G}_{2})$.

Definition 6²⁰

Let $\mathcal {G}$=$\left( \alpha ,\beta ,\gamma \right)$, $\mathcal {G}_{1}$=$\left( \alpha _{1},\beta _{1},\gamma _{1}\right)$$\mathcal {G}_{2}$=$\left( \alpha _{2},\beta _{2},\gamma _{2}\right)$ be the three IVPFEs, $\acute{a}$ is a real number such that $\acute{a}$ > 0, then fundamental operations are established as:

• i) $\mathcal {G}_{1} \oplus \mathcal {G}_{2}$= $\left( \begin{array}{c} \left[ \begin{array}{c} \mathfrak {a}^{-}_{1}+\mathfrak {a}^{-}_{2}-\mathfrak {a}^{-}_{1}\mathfrak {a}^{-}_{2}, \mathfrak {a}^{+}_{1}+\mathfrak {a}^{+}_{2}-\mathfrak {a}^{+}_{1}\mathfrak {a}^{+}_{2} \end{array}\right] , \\ \left[ \mathfrak {b}^{-}_{1}\mathfrak {b}^{-}_{2},\mathfrak {b}^{+}_{1}\mathfrak {b}^{+}_{2}\right] , \\ \left[ \mathfrak {c}^{-}_{1}\mathfrak {c}^{-}_{2},\mathfrak {c}^{+}_{1}\mathfrak {c}^{+}_{2}\right] \end{array}\right)$,

• ii) $\mathcal {G}_{1} \otimes \mathcal {G}_{2}$= $\left( \begin{array}{c} \left[ \mathfrak {a}^{-}_{1}\mathfrak {a}^{-}_{2},\mathfrak {a}^{+}_{1}\mathfrak {a}^{+}_{2}\right] , \\ \left[ \begin{array}{c} \mathfrak {b}^{-}_{1}+\mathfrak {b}^{-}_{2}-\mathfrak {b}^{-}_{1}\mathfrak {b}^{-}_{2}, \mathfrak {b}^{+}_{1}+\mathfrak {b}^{+}_{2}-\mathfrak {b}^{+}_{1}\mathfrak {b}^{+}_{2} \end{array}\right] , \\ \left[ \begin{array}{c} \mathfrak {c}^{-}_{1}+\mathfrak {c}^{-}_{2}-\mathfrak {c}^{-}_{1}\mathfrak {c}^{-}_{2}, \mathfrak {c}^{+}_{1}+\mathfrak {c}^{+}_{2}-\mathfrak {c}^{+}_{1}\mathfrak {c}^{+}_{2} \end{array}\right] \end{array}\right)$,

• iii) $\acute{a} \mathcal {G}$= $\left( \begin{array}{c} \left[ 1-\left( 1-\mathfrak {a}^{-}\right) ^{\acute{a}}, 1-\left( 1-\mathfrak {a}^{+}\right) ^{\acute{a}} \right] , \\ \left[ \left( \mathfrak {b}^{-}\right) ^{\acute{a}},\left( \mathfrak {b}^{+}\right) ^{\acute{a}}\right] , \\ \left[ \left( \mathfrak {c}^{-}\right) ^{\acute{a}},\left( \mathfrak {c}^{+}\right) ^{\acute{a}}\right] \end{array}\right)$,

• iv) $\mathcal {G}^{\acute{a}}$= $\left( \begin{array}{c} \left[ \left( \mathfrak {a}^{-}\right) ^{\acute{a}},\left( \mathfrak {a}^{+}\right) ^{\acute{a}}\right] , \\ \left[ 1-\left( 1-\mathfrak {b}^{-}\right) ^{\acute{a}}, 1-\left( 1-\mathfrak {b}^{+}\right) ^{\acute{a}}\right] , \\ \left[ 1-\left( 1-\mathfrak {c}^{-}\right) ^{\acute{a}}, 1-\left( 1-\mathfrak {c}^{+}\right) ^{\acute{a}}\right] \end{array}\right)$,

• v) $\mathcal {G}^{c}$= $\left( \begin{array}{c} \left[ \mathfrak {c}^{-},\mathfrak {c}^{+}\right] , \left[ \mathfrak {b}^{-},\mathfrak {b}^{+}\right] , \left[ \mathfrak {a}^{-},\mathfrak {a}^{+}\right] \end{array}\right)$.

Proposed MSM operators

In this part, we apply the PMSM operator on IVPFEs and develop two novel operators which are known as IVPFPMSM and WIVPFPMSM:

IVPFPMSM aggregation operators

Definition 7

Let ${\mathcal {G}}_1$, $\mathcal {G}_2,...,$${\mathcal {G}}_n$ be a range of n IVPFEs. Then, the IVPFPMSM operator is defined as:

$$\begin{aligned} IVPHFPMSM^{(\delta )} \left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \frac{1}{\mathfrak {m}}\oplus ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( \frac{\oplus _{1\le k_1<...<k_l\le o_\mathfrak {h}\left( \otimes ^{\delta }_{l=1}{\mathcal {G}_k}_{l}\right) }}{C^{\delta }_{o_\mathfrak {h}}}\right) ^{\frac{1}{\delta }}, \end{aligned}$$

(8)

where $\mathfrak {m}$ represents the count of categories, $\delta$ is a parameter taking values from 1 to $o_\mathfrak {h}$, and $o_\mathfrak {h}$ signifies the count of criteria in category $\mathfrak {m}_\mathfrak {h}$, $\left( k_1,k_2,...,k_{\delta } \right)$ encompasses all the $\delta$-pairs of $\left( 1,2,...,o_{\mathfrak {h}} \right)$. The expression $C^{\delta }_{o_\mathfrak {h}}$ denotes the binomial coefficient and is defined as $C^{\delta }_{o_\mathfrak {h}}=\frac{o_\mathfrak {h}!}{\delta !\left( o_\mathfrak {h}-\delta \right) !}$.

Theorem 1

For given IVPFEs ${\mathcal {G}}_\mathfrak {s}$$\left( \mathfrak {s}=1,2,...,n\right)$. The aggregated outcome of Eq. (8) remains IVPFEs, outlined as follows:

$$\begin{aligned} IVPFPMSM^{(\delta )} = \left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}, \\ 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) . \end{aligned}$$

(9)

Proof

By the operational laws of IVPFEs, we can write

$$\begin{aligned} \otimes ^{\delta }_{l=1}\mathcal {G}_{\mathfrak {s}_{l}}= & \left( \begin{array}{c} \left[ \prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}},\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right] , \left[ 1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\biggr ),1-\prod \limits ^{\delta }_ {l=1}\biggl (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\biggr )\right] , \\ \left[ 1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\biggr ),1-\prod \limits ^{\delta }_{l=1} \biggl (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\biggr )\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \oplus _{1<\mathfrak {s}_{1}<....<\mathfrak {s}_{k}<o_\mathfrak {h}}\biggl (\otimes ^{\delta }_{l=1}\mathcal {G}_{\mathfrak {s}_{l}}\biggr )= \left( \begin{array}{c} \left[ \begin{array}{c} 1-\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr ), \\ 1-\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr ) \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits _{1<\mathfrak {s}_{1}<...<0_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr ),\\ \prod \limits _{1<\mathfrak {s}_{1}<...<0_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr ) \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits _{1<\mathfrak {s}_{1}<...<0_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr ),\\ \prod \limits _{1<\mathfrak {s}_{1}<...<0_\mathfrak {h}}\biggl (1-\prod \limits ^{\delta }_{l=1}\biggl (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr ) \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \left( \frac{\oplus _{1<\mathfrak {s}_{1}<....<\mathfrak {s}_{k}<0_\mathfrak {h}}(\otimes ^{\delta }_{l=1}\mathcal {G}_{\mathfrak {s}_{l}})}{C^{\delta }_{o_\mathfrak {h}}}\right) ^{\frac{1}{\delta }}= \left( \begin{array}{c} \left[ \begin{array}{c} \biggl (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\biggr )^{\frac{1}{\delta }},\\ \biggl (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\biggr )^{\frac{1}{\delta }} \end{array}\right] , \\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta },\\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta } \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta },\\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta } \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \otimes ^t_{\mathfrak {h}=1}\left( \frac{\oplus _{1<\mathfrak {s}_{1}<....<\mathfrak {s}_{k}<0_\mathfrak {h}}(\otimes ^{\delta }_{l=1}\mathcal {G}_{\mathfrak {s}_{l}})}{C^{\delta }_{o_\mathfrak {h}}}\right) ^{\frac{1}{\delta }}= \left( \begin{array}{c} \left[ \begin{array}{c} 1-\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\biggl (1-\biggl (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\biggr )^{\frac{1}{\delta }}\biggr ),\\ 1-\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\biggl (1-\biggl (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\biggr )^{\frac{1}{\delta }}\biggr ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1- \prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg ),\\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1- \prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1- \prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg ),\\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1- \prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg ) \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \frac{1}{\mathfrak {m}}\otimes ^t_{\mathfrak {h}=1}\bigg (\frac{\oplus _{1<\mathfrak {s}_{1}<....<\mathfrak {s}_{k}<0_\mathfrak {h}} (\otimes ^{\delta }_{l=1}\mathcal {G}_{\mathfrak {s}_{l}})}{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{\delta }}= \left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}, \\ 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) . \end{aligned}$$

This completes the verification. $\square$

Likewise, we can also find the IVPHFPMSM operator has some features, including idempotency, monotonicity, and boundedness.

Theorem 2

(Idempotincy) If the given IVPFEs$\mathcal {G}_{\mathfrak {s}}(\mathfrak {s}=1,2,3,...,n)$ are same i.e., $\mathcal {G}$=$\mathcal {G}_{\mathfrak {s}}(\mathfrak {s}=1,2,...,n)$.

$$\begin{aligned} IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\mathcal {G}. \end{aligned}$$

(10)

Proof

By Eq. (9), we have

$$\begin{aligned} IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}, \\ 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} = \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-(\mathfrak {a}^{-})^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-(\mathfrak {a}^{+})^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {b}^{-}\bigg )^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {b}^{+}\bigg )^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {c}^{-}\bigg )^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {c}^{+}\bigg )^{\delta }\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} = \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-(\mathfrak {a}^{-})^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-(\mathfrak {a}^{+})^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-\bigg (1-\mathfrak {b}^{-}\bigg )^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-\bigg (1-\mathfrak {b}^{+}\bigg )^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-\bigg (1-\mathfrak {c}^{-}\bigg )^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\bigg (1-\bigg (1-\mathfrak {c}^{+}\bigg )^{\delta }\bigg ) ^{C^{\delta }_{o_\mathfrak {h}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} = \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg ( 1-\bigg (1-\bigg (1-(\mathfrak {a}^{-})^{\delta }\bigg )\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ 1-\bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg ( 1-\bigg (1-\bigg (1-(\mathfrak {a}^{+})^{\delta }\bigg )\bigg )^{\frac{1}{\delta }}\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (1-\bigg (1-\mathfrak {b}^{-}\bigg ) ^{\delta }\bigg )\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (1-\bigg (1-\mathfrak {b}^{+}\bigg ) ^{\delta }\bigg )\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (1-\bigg (1-\mathfrak {c}^{-}\bigg ) ^{\delta }\bigg )\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}},\\ \bigg (\prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (1-\bigg (1-\mathfrak {c}^{+}\bigg ) ^{\delta }\bigg )\bigg )^\frac{1}{\delta }\bigg )\bigg )^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} =\left( \begin{array}{c} \left[ 1-\bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1-\mathfrak {a}^{-}\bigg )\bigg )^\frac{1}{\mathfrak {m}}, 1-\bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1-\mathfrak {a}^{+}\bigg )\bigg )^\frac{1}{\mathfrak {m}}\right] ,\\ \left[ \bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\mathfrak {b}^{-}\bigg )\bigg )\bigg )^\frac{1}{\mathfrak {m}}, \bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\mathfrak {b}^{+}\bigg )\bigg )\bigg )^\frac{1}{\mathfrak {m}}\right] ,\\ \left[ \bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\mathfrak {c}^{-} \bigg )\bigg )\bigg )^\frac{1}{\mathfrak {m}},\bigg (\prod \limits ^{t}_{\mathfrak {h}=1}\bigg (1- \bigg (1-\mathfrak {c}^{+}\bigg )\bigg )\bigg )^\frac{1}{\mathfrak {m}}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} =\left\{ [\mathfrak {a}^{-},\mathfrak {a}^{+}],[\mathfrak {b}^{-},\mathfrak {b}^{+}],[\mathfrak {c}^{-},\mathfrak {c}^{+}]\right\} =\mathcal {G}. \end{aligned}$$

$\square$

Theorem 3

(Monotonicity) Let $\mathcal {G}_{1},\mathcal {G}_{2},...,\mathcal {G}_{n}$ be IVPFEs where $\mathcal {G}_{\mathfrak {s}}$=$([\mathfrak {a}^{-}_{\mathfrak {s}},\mathfrak {a}^{+}_{\mathfrak {s}}] ,[\mathfrak {b}^{-}_{\mathfrak {s}},\mathfrak {b}^{+}_{\mathfrak {s}}],[\mathfrak {c}^{-}_{\mathfrak {s}},\mathfrak {c}^{+}_{\mathfrak {s}}])$ and $\mathfrak {s}=1,2,...,n$ and let $\mathcal {G^{'}}_{1},\mathcal {G^{'}}_{2},...,\mathcal {G^{'}}_{n}$ where $\mathcal {G}^{'}_{\mathfrak {s}}$=$([\mathfrak {a}^{'-}_{\mathfrak {s}},\mathfrak {a}^{'+}_{\mathfrak {s}}], [\mathfrak {b}^{'-}_{\mathfrak {s}},\mathfrak {b}^{'+}_{\mathfrak {s}}],[\mathfrak {c}^{'-}_{\mathfrak {s}}, \mathfrak {c}^{'+}_{\mathfrak {s}}])$ be two collection of IVPFEs and $\mathfrak {s}=1,2,...,n$ which meet the condition $\mathfrak {a}^{-}_{\mathfrak {s}}$$\ge$$\mathfrak {a}^{'-}_{\mathfrak {s}}$,$\mathfrak {a}^{+}_{\mathfrak {s}}$$\ge$$\mathfrak {a}^{'+}_{\mathfrak {s}}$, $\mathfrak {b}^{-}_{\mathfrak {s}}$$\le$$\mathfrak {b}^{'-}_{\mathfrak {s}}$,$\mathfrak {b}^{+}_{\mathfrak {s}}$$\le$$\mathfrak {b}^{'+}_{\mathfrak {s}}$, $\mathfrak {c}^{-}_{\mathfrak {s}}$$\ge$$\mathfrak {c}^{'-}_{\mathfrak {s}}$, and $\mathfrak {c}^{+}_{\mathfrak {s}}$$\ge$$\mathfrak {c}^{'+}_{\mathfrak {s}}$ for all $\mathfrak {s}=1,2,...,n$. Then $\mathfrak {s}=1,2,...,n$. Then

$$\begin{aligned} IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \ge IVPFPMSM^{(\delta )} \left( {\mathcal {G}}^{'}_{1},{\mathcal {G}}^{'}_{2},...,{\mathcal {G}}_{n} \right) . \end{aligned}$$

(11)

Proof

we can capture that ${\delta }$$\ge$ 1 and $C^{\delta }_{o_\mathfrak {h}}$$\ge$ 1 easily. Since, $\mathfrak {a}^{-}_{\mathfrak {s}}$$\ge$$\mathfrak {a}^{'-}_{\mathfrak {s}}$,$\mathfrak {a}^{+}_{\mathfrak {s}}$$\ge$$\mathfrak {a}^{'+}_{\mathfrak {s}}$, $\mathfrak {b}^{-}_{\mathfrak {s}}$$\le$$\mathfrak {b}^{'-}_{\mathfrak {s}}$,$\mathfrak {b}^{+}_{\mathfrak {s}}$$\le$$\mathfrak {b}^{'+}_{\mathfrak {s}}$, $\mathfrak {c}^{-}_{\mathfrak {s}}$$\ge$$\mathfrak {c}^{'-}_{\mathfrak {s}}$, and $\mathfrak {c}^{+}_{\mathfrak {s}}$$\ge$$\mathfrak {c}^{'+}_{\mathfrak {s}}$ for all $\mathfrak {s}=1,2,...,n$. Thus it hold the following inequalities:

First, we take the membership part,

$$\begin{aligned} & 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \ge 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{'-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{aligned}$$

$$\begin{aligned} & 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( \mathfrak {a}_{il}\right) ^{-}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \ge 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( \mathfrak {a}^{'}_{\mathfrak {s}_{l}}\right) ^{-}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{aligned}$$

$$\begin{aligned} & 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \ge 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{'}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}. \end{aligned}$$

Now we take the neutral part,

$$\begin{aligned} & \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \le \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{'-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{aligned}$$

$$\begin{aligned} & \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\left( \mathfrak {b}_{\mathfrak {s}_{l}}\right) ^{-}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \le \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\left( \mathfrak {b}^{'}_{\mathfrak {s}_{l}}\right) ^{-}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{aligned}$$

and

$$\begin{aligned} & \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}} \right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}\\ & \qquad \le \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{'}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{aligned}$$

which implies that,

$$\begin{aligned} \left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}, \\ 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) \ge \\ \left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{'-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}}, \\ 1-\left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{'+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{'-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{'+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{'-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}}, \\ \left( \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( 1-\left( 1-\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{'+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) . \end{aligned}$$

Hence, $IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \ge IVPFPMSM^{(\delta )} \left( {\mathcal {G}}^{'}_{1},{\mathcal {G}}^{'}_{2},...,{\mathcal {G}}_{n} \right)$.$\square$

Theorem 4

(Boundedness) for a given IVPFEs suppose that $\mathcal {G}^{-}$=$\min _{\mathfrak {s}}{\mathcal {G}_{\mathfrak {s}}}$ and $\mathcal {G}^{+}$=$\max _{\mathfrak {s}}{\mathcal {G}_{\mathfrak {s}}}$ and ($\mathfrak {s}=1,2,...,n$), then

$$\begin{aligned} \mathcal {G}^{-} \le IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \le \mathcal {G}^{+}. \end{aligned}$$

(12)

Proof

As given that $\mathcal {G}^{-}$=$\min _{\mathfrak {s}}{\mathcal {G}_{\mathfrak {s}}}$$\le$${\mathcal {G}_{\mathfrak {s}}}$ from Theorem 2 and 3, we can write

$$\begin{aligned} \mathcal {G}^{-}=IVPFPMSM^{(\delta )}\left( {\mathcal {G}^{-}},{\mathcal {G}^{-}},...,{\mathcal {G}^{-}} \right) \le IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) . \end{aligned}$$

Similarly, we have

$$\begin{aligned} IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \le IVPFPMSM^{(\delta )}\left( {\mathcal {G}^{+}},{\mathcal {G}^{+}},...,{\mathcal {G}^{+}} \right) =\mathcal {G}^{+}. \end{aligned}$$

Thus, we get

$$\begin{aligned} \mathcal {G}^{-} \le IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \le \mathcal {G}^{+}. \end{aligned}$$

$\square$

Theorem 5

For given range of IVPFEs$\mathcal {G}_{\mathfrak {s}} (\mathfrak {s}=1,2,...,n)$ , $l=1,2,...,\min _{\mathfrak {h}}{o_{\mathfrak {h}}}$. Then

$$\begin{aligned} \min \left\{ {IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) }\right\} = IVPFPMSM^{(\min _{\mathfrak {h}}\left\{ o_\mathfrak {h}\right\} )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \end{aligned}$$

$$\begin{aligned} \begin{aligned}= & \left( \begin{array}{c} \left[ \begin{array}{c} 1-\left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{o_\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}}, 1-\left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1-\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{o_\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}} \end{array}\right] ,\\ \left[ \begin{array}{c} \left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_{\mathfrak {h}}} \left( \mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}}, \left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_{\mathfrak {h}}} \left( \mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}} \end{array}\right] ,\\ \left[ \begin{array}{c} \left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_{\mathfrak {h}}} \left( \mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}}, \left( \prod \limits _{\mathfrak {h}=1}^{t}\left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_{\mathfrak {h}}} \left( \mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) ^\frac{1}{\mathfrak {h}}\right) ^\frac{1}{\mathfrak {m}} \end{array}\right] \end{array}\right) , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \max \left\{ {IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) }\right\} = IVPFPMSM^{(1)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) . \end{aligned}$$

We will now investigate several distinct cases of the IVPFPMSM operator with different parameter values for l.

Case 1

Suppose there is a single category $\mathfrak {m}_{1}$ with n sets and a parameter $\delta$ associated with the IVPFPMSM operator. In this scenario, we obtain:

$$\begin{aligned} IVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \left( \begin{array}{c} \left[ \begin{array}{c} 1 - \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^{\frac{1}{1}},\\ 1 - \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^{\frac{1}{\delta }}\right) \right) ^{\frac{1}{1}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^{\frac{1}{1}}, \\ \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^{\frac{1}{1}} \end{array}\right] , \\ \left[ \begin{array}{c} \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^{\frac{1}{1}}, \\ \left( \prod \limits ^{1}_{\mathfrak {h}=1}\left( 1 - \left( 1 - \left( \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\left( 1 - \prod \limits ^{\delta }_{l=1}\left( 1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\right) \right) \right) ^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\right) ^\frac{1}{\delta }\right) \right) ^{\frac{1}{1}} \end{array}\right] \end{array}\right) , \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }}, \\ \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{\delta }_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\delta }} \end{array}\right] , \\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}} \bigg )^\frac{1}{\delta }, \\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}} \bigg )^\frac{1}{\delta } \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}} \bigg )^\frac{1}{\delta }, \\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}} \bigg )^\frac{1}{\delta } \end{array}\right] \end{array}\right) , \end{aligned}$$

(13)

this simplifies to IVPF MSM operator¹⁹.

Case 2

If $\mathfrak {m}=1$ and $\delta =1$, according to the definition of the IVPFPMSM operator, we obtain:

$$\begin{aligned} IVPFPMSM^{(1)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{1}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg )\bigg )^\frac{1}{1}, \\ 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{1}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg )\bigg )^\frac{1}{1} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{1}\bigg )\bigg )^{\frac{1}{1}}, \\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{1}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{1}\bigg )\bigg )^{\frac{1}{1}}, \\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{1}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} 1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{\mathfrak {s}_{1}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}, 1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}, \bigg (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}, \bigg (\prod \limits _{1<\mathfrak {s}_{1}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \end{array}\right] \end{array}\right) let \left( \mathfrak {s}_{1}=k\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad =\left( \begin{array}{c} \left[ 1-\biggl (\prod \limits _{k=1}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{k}\biggr )\biggr )^{\frac{1}{o_\mathfrak {h}}}, 1-\biggl (\prod \limits _{k=1}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{k}\biggr )\biggr )^{\frac{1}{o_\mathfrak {h}}}\right] , \\ \left[ \bigg (\prod \limits _{k=1}^{o_\mathfrak {h}} \mathfrak {b}^{-}_{k}\bigg )^{\frac{1}{o_\mathfrak {h}}},\bigg (\prod \limits _{k=1}^{o_\mathfrak {h}} \mathfrak {b}^{+}_{k}\bigg )^{\frac{1}{o_\mathfrak {h}}}\right] , \left[ \bigg (\prod \limits _{k=1}^{o_\mathfrak {h}} \mathfrak {c}^{-}_{k}\bigg )^{\frac{1}{o_\mathfrak {h}}},\bigg (\prod \limits _{k=1}^{o_\mathfrak {h}} \mathfrak {c}^{+}_{k}\bigg )^{\frac{1}{o_\mathfrak {h}}}\right] \end{array}\right) , \end{aligned}$$

(14)

this simplifies to the IVPF averaging operator³⁴.

Case 3

If $\mathfrak {m}=1$ and $\delta =2$, according to the definition of the IVPFPMSMS operator, we obtain:

$$\begin{aligned} IVPFPMSM^{(2)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{2}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}}\bigg )\bigg )^\frac{1}{1}, \\ 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{2}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}}\bigg )\bigg )^\frac{1}{1} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{1}}, \\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{1}}, \\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{\mathfrak {s}_{1}}\mathfrak {a}^{-}_{\mathfrak {s}_{2}}\biggr )\biggr )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}}, \\ \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\biggr )\biggr )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}} \end{array}\right] , \\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}, \\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\mathfrak {b}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2}, \\ 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (1-\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{2} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{\mathfrak {s}_{1}}\mathfrak {a}^{-}_{\mathfrak {s}_{2}}\biggr ) \biggr )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}}, \bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\biggr ) \biggr )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\mathfrak {b}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1-\biggl (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{\mathfrak {s}_{1}}\mathfrak {a}^{-}_{\mathfrak {s}_{2}}\biggr ) \biggr )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}}, \bigg (1-\biggl (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\biggr )\biggr )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\mathfrak {b}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{2}.\frac{2}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1-\biggl (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{-}_{\mathfrak {s}_{1}}\mathfrak {a}^{-}_{\mathfrak {s}_{2}} \biggr )\biggr )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}}, \bigg (1-\biggl (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \biggl (1-\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\mathfrak {a}^{+}_ {\mathfrak {s}_{2}}\biggr )\biggr )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}}\bigg )^{\frac{1}{2}} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\mathfrak {b}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2}, 1-\bigg (1-\bigg (\prod \limits _{\mathfrak {s}_{1},\mathfrak {s}_{2}=1;\mathfrak {s}_{1}\ne \mathfrak {s}_{2}}^{o_\mathfrak {h}} \bigg (\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )\bigg )^{\frac{1}{o_{\mathfrak {h}}(o_{\mathfrak {h}}-1)}} \bigg )^\frac{1}{2} \end{array}\right] \end{array}\right) , \end{aligned}$$

(15)

this simplifies to the IVPF Bonferronin mean operator $IVPFBM^{(1,1)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right)$.

Case 4

If $\mathfrak {m}=1$ and $\delta =n$, according to the definition of the IVPFPMSM operator, we obtain:

$$\begin{aligned} IVPFPMSM^{(n)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\bigg )\bigg )^\frac{1}{1}, \\ 1-\bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\biggr )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\bigg )\bigg )^\frac{1}{1} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{o_\mathfrak {h}}\bigg )\bigg )^{\frac{1}{1}},\\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{o_\mathfrak {h}}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{o_\mathfrak {h}}\bigg )\bigg )^{\frac{1}{1}},\\ \bigg (\prod \limits ^{1}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}} \bigg )^\frac{1}{o_\mathfrak {h}}\bigg )\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ =\left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\bigg )^{\frac{1}{o_\mathfrak {h}}},\bigg (1- \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\bigg )^{\frac{1}{o_\mathfrak {h}}} \end{array}\right] , \\ \left[ \begin{array}{c} 1-\bigg (1- \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg ) \bigg )^\frac{1}{\delta }, 1-\bigg (1- \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg ) \bigg )^\frac{1}{\delta } \end{array}\right] ,\\ \left[ \begin{array}{c} 1-\bigg (1- \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg ) \bigg )^\frac{1}{\delta }, 1-\bigg (1- \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg ) \bigg )^\frac{1}{\delta } \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} =\left( \begin{array}{c} \left[ \bigg (1- \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\biggr )\bigg )^{\frac{1}{o_\mathfrak {h}}}, \bigg (1- \biggl (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\biggr )\bigg )^{\frac{1}{o_\mathfrak {h}}}\right] ,\\ \left[ 1-\bigg (\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg ) \bigg )^\frac{1}{o_\mathfrak {h}}, 1-\bigg (\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg ) \bigg )^\frac{1}{o_\mathfrak {h}}\right] ,\\ \left[ 1-\bigg (\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg ) \bigg )^\frac{1}{o_\mathfrak {h}}, 1-\bigg (\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg ) \bigg )^\frac{1}{o_\mathfrak {h}}\right] \end{array}\right) , \end{aligned}$$

(16)

which simplifies to the IVPF geometric mean operator³⁴.

Example 1

Let $\mathcal {G}_{1}$$=$$\left\{ [0.2,0.4],[0.1,0.15],[0.25,0.35]\right\}$, $\mathcal {G}_{2}$$=$$\left\{ [0.35,0.4],[0.03,0.05],[0.3,0.55]\right\}$, $\mathcal {G}_{3}$$=$$\left\{ [0.1,0.15],[0.25,0.3],[0.4,0.5]\right\}$ and $\mathcal {G}_{4}$$=$$\left\{ [0.45,0.5],[0.3,0.35],[0.05,0.1]\right\}$ be four IVPFEs. Suppose these four IVPFEs are categorized into two categories $L_{1}$ and $L_{2}$ with $\mathfrak {U}_{1}$= $\left\{ \mathcal {G}_{1},\mathcal {G}_{3}\right\}$ and $\mathfrak {U}_{2}$ = $\left\{ \mathcal {G}_{2},\mathcal {G}_{4}\right\}$. Here, we apply the IVPFPMSM operator to aggregate this IVPFEs. In general, we let $\delta$ = 2, then

$$\begin{aligned} IVPFPMSM^{(\delta )} \left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \left( \begin{array}{c} \left[ \begin{array}{c} 1-\bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\biggl (1-\prod \limits ^{2}_{l=1}\mathfrak {a}^{+}_{\mathfrak {s}_{l}} \biggr )\biggr )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}}\bigg )\bigg )^\frac{1}{2},\\ 1-\bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\biggl (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\biggl (1-\prod \limits ^{2}_{l=1}\mathfrak {a}^{-}_{\mathfrak {s}_{l}} \biggr )\biggr )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{2}}\bigg )\bigg )^\frac{1}{2} \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1} \bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{2}},\\ \bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1} \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{2}} \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1} \bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{2}},\\ \bigg (\prod \limits ^{2}_{\mathfrak {h}=1}\bigg (1-\bigg (1-\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1} \bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )\bigg )\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^\frac{1}{2}\bigg )\bigg )^{\frac{1}{2}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} =\left( [0.2803, 0.3540],[0.1772, 0.2213],[0.2464, 0.3954]\right) . \end{aligned}$$

WIVPFPMSM aggregation operators

In this section, we introduce the WIVPFPMSM operator, assuming that all criteria carry equal importance. However, in practical DM, their weights are not uniform. Therefore, it becomes crucial to acknowledge that each criterion possesses its individual weight. Consider the weight of each criteria, denoted as $\mathcal {G}_{\mathfrak {s}}$ (for $\mathfrak {s}=1,2,...,n$), with $\mathfrak {w_{\mathfrak {s}}}$ satisfying $0\le \mathfrak {w_{\mathfrak {s}}}\le 1$ and $\sum \limits ^{n}_{\mathfrak {s}=1}\mathfrak {w_{\mathfrak {s}}}=1$. The resulting WIVPFPMSM operator for IVPFEs is then characterized as follows.

Definition 8

Let ${\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n$ be a range of nIVPFEs. Then, the WIVPFPMSM operator is characterized as:

$$\begin{aligned} \begin{aligned} WIVPFPMSM^{(\delta )} \left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \frac{1}{\mathfrak {m}}\oplus ^{\mathfrak {m}}_{\mathfrak {h}=1}\left( \frac{\oplus _{1\le k_1<...<k_l\le o_\mathfrak {h}\left( \otimes ^{\delta }_{l=1}\left( {\mathcal {G}_k}_{l}\right) ^{\mathfrak {W}_{kl}}\right) }}{C^{\delta }_{o_\mathfrak {h}}}\right) ,&\end{aligned} \end{aligned}$$

(17)

where $\mathfrak {m}$ represents the count of categories, $\delta$ is a parameter taking values from 1 to $o_\mathfrak {h}$, and $o_\mathfrak {h}$ signifies the count of criteria in category $\mathfrak {m}_\mathfrak {h}$, $\left( k_1,k_2,...,k_{\delta } \right)$ encompasses all the $\delta$-pairs of $\left( 1,2,...,o_{\mathfrak {h}} \right)$. The expression $C^{\delta }_{o_\mathfrak {h}}$ denotes the binomial coefficient and is defined as $C^{\delta }_{o_\mathfrak {h}}=\frac{o_\mathfrak {h}!}{\delta !\left( o_\mathfrak {h}-\delta \right) !}$ and $\mathfrak {w}_{l}$$\ge$ 0 show the weight obeying $\sum \limits ^{m}_{l=1}\mathfrak {w_{l}}$=1.

Theorem 6

For given IVPFEs ${\mathcal {G}}_{\mathfrak {s}}$$\left( \mathfrak {s}=1,2,...,n\right)$. The aggregated result of Eq. (19) is still IVPFE, characterized as below:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}\bigg ), \\ \bigg (1- \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}, \\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}, \\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}} \end{array}\right] \end{array}\right) . \end{aligned}$$

(18)

Proof

Following the principles outlined in Theorem 1, it can be straightforwardly demonstrated.$\square$

Theorem 7

(Idempotincy) If the domain of discourse of given IVPFEs$\mathcal {G}_{\mathfrak {s}}$$(\mathfrak {s}=1,2,...,n)$ are same i.e., $\mathcal {G}_{\mathfrak {s}}$$(\mathfrak {s}=1,2,...,n)$. Then

$$\begin{aligned} WIVPFPMSM^{(\delta )} \left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\mathcal {G}. \end{aligned}$$

(19)

Theorem 8

(Monotonicity) $\mathcal {G}_{1},\mathcal {G}_{2},...,\mathcal {G}_{n}$ be IVPFEs where $\mathcal {G}_{\mathfrak {s}}$=$\left( \left[ \mathfrak {a}^{-}_{\mathfrak {s}},\mathfrak {a}^{+}_{\mathfrak {s}}\right] ,\left[ \mathfrak {b}^{-}_{\mathfrak {s}},\mathfrak {b}^{+}_{\mathfrak {s}}\right] ,\left[ \mathfrak {c}^{-}_{\mathfrak {s}},\mathfrak {c}^{+}_{\mathfrak {s}}\right] \right)$and $\mathfrak {s}=1,2,...,n$ and let $\mathcal {G}^{'}_{1},\mathcal {G}^{'}_{2},...,\mathcal {G}^{'}_{n}$ where $\mathcal {G}^{'}_{\mathfrak {s}}$=$\left( \left[ \mathfrak {a}^{'-}_{\mathfrak {s}},\mathfrak {a}^{'+}_{\mathfrak {s}}\right] ,\left[ \mathfrak {b}^{'-}_{\mathfrak {s}},\mathfrak {b}^{'+}_{\mathfrak {s}}\right] ,\left[ \mathfrak {c}^{'-}_{\mathfrak {s}},\mathfrak {c}^{'+}_{\mathfrak {s}}\right] \right)$ and $\mathfrak {s}=1,2,...,n$ which meet the condition $\left[ \mathfrak {a}^{-}_{\mathfrak {s}},\mathfrak {a}^{+}_{\mathfrak {s}}\right]$$\ge$$\left[ \mathfrak {a}^{'-}_{\mathfrak {s}},\mathfrak {a}^{'+}_{\mathfrak {s}}\right]$, $\left[ \mathfrak {b}^{-}_{\mathfrak {s}},\mathfrak {b}^{+}_{\mathfrak {s}}\right]$$\le$$\left[ \mathfrak {b}^{'-}_{\mathfrak {s}},\mathfrak {b}^{'+}_{\mathfrak {s}}\right]$ and $\left[ \mathfrak {c}^{-}_{\mathfrak {s}},\mathfrak {c}^{+}_{\mathfrak {s}}\right]$$\le$$\left[ \mathfrak {c}^{'-}_{\mathfrak {s}},\mathfrak {c}^{'+}_{\mathfrak {s}}\right]$ for all $\mathfrak {s}=1,2,...,n$. Then

$$\begin{aligned} \begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \ge WIVPFPMSM{(\delta )} \left( {\mathcal {G}}^{'}_{1},{\mathcal {G}}^{'}_{2},...,{\mathcal {G}}^{'}_{n} \right) .&\end{aligned} \end{aligned}$$

(20)

Theorem 9

(Boundedness) Let ${\mathcal {G}}_{\mathfrak {s}}$ be the domain of discourse of IVPFEs for $\mathfrak {s}=1,2,...,n$ and $\mathcal {G}^{-}$=$\min _{\mathfrak {s}}{\mathcal {G}_{\mathfrak {s}}}$ and $\mathcal {G}^{+}$=$\max _{\mathfrak {s}}{\mathcal {G}_{\mathfrak {s}}}$. Then

$$\begin{aligned} \mathcal {G}^{-}\le WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \le \mathcal {G}^{+}. \end{aligned}$$

(21)

Theorem 10

For given range of IVPFEs$\mathcal {G}_{\mathfrak {s}} (\mathfrak {s}=1,2,...,n)$ , $l=1,2,...,\min _{\mathfrak {h}}{o_{\mathfrak {h}}}$. Then

$$\begin{aligned} \min \left\{ {WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) }\right\} = WIVPFPMSM^{(\min _{\mathfrak {h}}\left\{ o_\mathfrak {h}\right\} )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) \end{aligned}$$

$$\begin{aligned} = \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1} \bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )\bigg ), \bigg (1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1} \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ), \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}} \bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ) \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1} \bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ), \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1} \bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ) \end{array}\right] \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \max \left\{ {WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) }\right\} = WIVPHFPMSM^{(1)}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) . \end{aligned}$$

Now examine numerous peculiar instances of the WIVPFPMSM operator concerning various parameter l values.

Case 1

Suppose there is only one category $\mathfrak {m}_{1}$ with n sets, and a parameter $\delta$ associated with the WIVPFPMSM operator. In this scenario, we have:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ), \\ \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) . \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad = \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )\bigg ),\\ \bigg (1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ), \\ \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ) \end{array}\right] ,\\ \left[ \begin{array}{c} \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ), \\ \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg ) \end{array}\right] \end{array}\right) , \end{aligned}$$

(22)

which simplifies to a WIVPFMSM operator¹⁹.

Case 2

Suppose there is only one category, denoted as $\mathfrak {m}=1$, and $\delta =1$ based on the WIVPFPMSM operator. In this case, we have:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ), \\ \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}, \\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}, \\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{1}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{1}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} = \left( \begin{array}{c} \left[ \begin{array}{c} 1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\bigg ), 1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\bigg ) \end{array}\right] , \\ \left[ \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}, \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\right] ,\\ \left[ \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}, \prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{o_\mathfrak {h}}}\right] \end{array}\right) , \end{aligned}$$

(23)

this simplifies to a weighted IVPF averaging operator³⁴.

Case 3

Suppose there is only one category, denoted as $\mathfrak {m}=1$, and $\delta =2$ based on the WIVPFPMSM operator. In this scenario, we have:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ),\\ \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{2}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{2}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ = \left( \begin{array}{c} \left[ \begin{array}{c} 1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}}\bigg (1-\bigg (\mathfrak {a}^{-}_ {\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}}\bigg (\mathfrak {a}^{-}_ {\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ),\\ 1- \bigg (\prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}} \bigg (1-\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}}\bigg (1- \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h}.\left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}}\bigg (1- \bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h}.\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}}\bigg ( 1-\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h} \left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits _{1<\mathfrak {s}_{1}<\mathfrak {s}_{2}<o_\mathfrak {h}}\bigg (1-\bigg (1 -\mathfrak {c}^{+}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{2}{{o_\mathfrak {h}.\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ = \left( \begin{array}{c} \left[ \begin{array}{c} 1- \bigg (\prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{2}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{2}\frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ),\\ 1- \bigg (\prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}} \bigg )^{\frac{1}{2}\frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}} \bigg )^{\frac{1}{2}\frac{2}{{o_\mathfrak {h} \left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1- \mathfrak {b}^{+}_{\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{ \mathfrak {s}_{1}}}.\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{2}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{2}\frac{2}{{o_\mathfrak {h}.\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {c}^{-}_ {\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_ {\mathfrak {s}_{2}}}\bigg )^{\frac{1}{2}.\frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {c}^{+}_ {\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{2} \frac{2}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad = \left( \begin{array}{c} \left[ \begin{array}{c} 1- \bigg (\prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{2}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ),\\ 1- \bigg (\prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {b}^{-}_ {\mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_ {\mathfrak {s}_{2}}}\bigg )^{\frac{1}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}}.\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{2}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {c}^{-}_{ \mathfrak {s}_{1}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}} \bigg )^{\frac{1}{{o_\mathfrak {h}\left( o_\mathfrak {h}-1\right) }}},\\ \prod \limits ^{o_\mathfrak {h}}_{\mathfrak {s}_{1}\ne \mathfrak {s}_{2}=1; \mathfrak {s}_{1}\ne \mathfrak {s}_{2}}\bigg (1-\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{1}} \bigg )^{\mathfrak {w}_{\mathfrak {s}_{1}}} \bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{2}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{2}}}\bigg )^{\frac{1}{{o_\mathfrak {h}.\left( o_\mathfrak {h}-1\right) }}} \end{array}\right] \end{array}\right) , \end{aligned}$$

(24)

this simplifies to a weighted IVPF Bonferroni mean operator $WIVPFPMSM^{(1,1)}\left( \mathcal {G}_{1},\mathcal {G}_{2},...,\mathcal {G}_{n}\right)$.

Case 4

Suppose there is only one category, denoted as $\mathfrak {m}=1$, and $\delta =o_{\mathfrak {h}}$ based on the WIVPFPMSM operator. In this situation, we have:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) =\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ),\\ \bigg (1- \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}}\bigg ) \end{array}\right] , \\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}},\\ \prod \limits ^{1}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{o_\mathfrak {h}}_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{1}} \end{array}\right] \end{array}\right) \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\ = \left( \begin{array}{c} \left[ \begin{array}{c} \prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}, \prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}} \end{array}\right] , \\ \left[ 1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}, 1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\right] ,\\ \left[ 1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}, 1-\prod \limits ^{o_\mathfrak {h}}_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\right] \end{array}\right) , \end{aligned}$$

this simplifies to a weighted IVPF geometric mean operator³⁴.

Proposed decision-making methodology

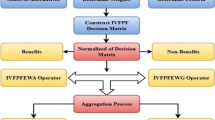
This segment is designed to structure the MCDM approach around emerging IVPFPMSM operators. Let R=$\left\{ \mathfrak {O}_{1}, \mathfrak {O}_{2},..., \mathfrak {O}_{x}\right\}$ represent the set of alternatives for each decision, S =$\left\{ \mathfrak {V}_{1}, \mathfrak {V}_{2},..., \mathfrak {V}_{y}\right\}$ be the set of choices, and $\mathfrak {w}$ =$\left( \mathfrak {w_{1}, w_{2},..., w_{n}}\right)$ be the weight vector for the criteria set S. Ensuring that $\sum \limits _{k=1}^{y}\mathfrak {w}_{k}$= 1 and $\mathfrak {w}_{k}$$\in [0,1]$, the weight vector $\mathfrak {w}$ is employed to express the relative importance of various criteria in the DM process. Decision-makers evaluate each alternative $\mathfrak {O}_{i}$ with respect to the criteria $\mathfrak {V}_{i}$. Assuming that S =$\left\{ \mathfrak {V}_{1}, \mathfrak {V}_{2},..., \mathfrak {V}_{y}\right\}$ is divided into $\mathfrak {m}$ distinct categories $\left\{ P_{1}, P_{2},..., P_{\mathfrak {m}}\right\}$. Criteria within the same category are interconnected, while no connections exist between criteria in different categories. The ensuing instances illustrate the demonstration of the main phases of the proposed approach as follows:

Step 1:

Construction of IVPF decision matrix: Given the mentioned context, the MCDM problem can be structured through the subsequent generation of a decision matrix as given in Eq. (25).

$$\begin{aligned} \textbf{P}_{x\times y} = \begin{pmatrix} \mathcal {G}_{11} & \dots & \mathcal {G}_{1g} & \dots & \mathcal {G}_{1y} \\ \vdots & \ddots & \ \vdots & \ddots & \vdots \\ \mathcal {G}_{\mathfrak {s}{1}} & \dots & \mathcal {G}_{\mathfrak {s}{g}} & \dots & \mathcal {G}_{\mathfrak {s}{y}} \\ \vdots & \ddots & \ \vdots & \ddots & \vdots \\ \mathcal {G}_{x1} & \dots & \mathcal {G}_{xg} & \dots & \mathcal {G}_{xy} \end{pmatrix}. \end{aligned}$$

(25)

Step 2:

Normalization: In this stage, the IVPF assessment matrix $\textbf{P}_{x\times y}$ undergoes modifications based on selected benefit and cost criteria. These two criteria exhibit contrasting behaviour, indicating that higher values favour the benefit criterion while adversely affecting the cost criterion. Consequently, we transform the cost criteria into benefit criteria, employing the subsequent normality method to ensure compliance with all requirements.

$$\begin{aligned} \mathcal {G}^{'}_{ig} = {\left\{ \begin{array}{ll} \mathcal {G}_{ig} , & \mathfrak {V}_{g} \text { is a befit criterion,}\\ \big (\mathcal {G}_{ig}\big )^{c}, & \mathfrak {V}_{g} \text { is cost criteria.} \end{array}\right. } \end{aligned}$$

(26)

Step 3:

Aggregation: Utilizing the introduced WIVPFPMSM method, we derive the aggregated assessment score for each alternative $\mathfrak {O}_{i}(i = 1, 2,..., x)$ as depicted below:

$$\begin{aligned} WIVPFPMSM^{(\delta )}\left( {\mathcal {G}}_1,{\mathcal {G}}_2,...,{\mathcal {G}}_n \right) = \left( \begin{array}{c} \left[ \begin{array}{c} \bigg (1- \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}\bigg ), \\ \bigg (1- \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (\mathfrak {a}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}\bigg ) \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}, \\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {b}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}} \end{array}\right] ,\\ \left[ \begin{array}{c} \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{-}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}}, \\ \prod \limits ^{\mathfrak {m}}_{\mathfrak {h}=1}\bigg (\prod \limits _{1<\mathfrak {s}_{1}<...<o_\mathfrak {h}}\bigg (1-\prod \limits ^{\delta }_{l=1}\bigg (1-\mathfrak {c}^{+}_{\mathfrak {s}_{l}}\bigg )^{\mathfrak {w}_{\mathfrak {s}_{l}}}\bigg )^{\frac{1}{C^{\delta }_{o_\mathfrak {h}}}}\bigg )^{\frac{1}{\mathfrak {m}}} \end{array}\right] \end{array}\right) . \end{aligned}$$

(27)

Where $\mathfrak {m}$ represents the count of categories, $\delta$ is a parameter taking values from 1 to $o_\mathfrak {h}$, and $o_\mathfrak {h}$ signifies the count of criteria in category $\mathfrak {m}_\mathfrak {h}$, $\left( k_1,k_2,...,k_{\delta } \right)$ encompasses all the $\delta$-pairs of $\left( 1,2,...,o_{\mathfrak {h}} \right)$. The expression $C^{\delta }_{o_\mathfrak {h}}$ denotes the binomial coefficient and is defined as $C^{\delta }_{o_\mathfrak {h}}=\frac{o_\mathfrak {h}!}{\delta !\left( o_\mathfrak {h}-\delta \right) !}$ and $\mathfrak {w}_{g}$$\ge$ 0 is the weight of the criteria $L_{g}$ (g=1,2,...,n) and $\mathcal {G}^{'}_{ig}$ normalized value of $\mathcal {G}_{ig}$ (g=1,2,...,n) which we take from Step 2.

Step 4:

Score values: From Eq. (6) , the score value of the aggregated IVPFEs $\mathcal {G}_{ig}$ (g=1,2,...,n) are determined.

Step 5:

Ordering of alternatives: In this final stage, the alternatives are sorted as per their score values, and the best solution is chosen.

Illustrative example

In this section, we address a DM problem by implementing our proposed strategy to evaluate and rank the considered alternatives.

Description

Consider a scenario where there are five viable enterprise resource management (ERM) systems denoted by $\left\{ \mathfrak {O}_{1}, \mathfrak {O}_{2}, \mathfrak {O}_{3},\mathfrak {O}_{4}, \mathfrak {O}_{5}\right\}$, representing the available alternatives that decision-makers need to assess. In this context, the evaluation of ERM systems is based on four attributes denoted by$\left\{ \mathfrak {V}_{1}, \mathfrak {V}_{2}, \mathfrak {V}_{3},\mathfrak {V}_{4}\right\}$, specifically: $\mathfrak {V}_{1}$: Technical Achievement, $\mathfrak {V}_{2}$: Human Resources, $\mathfrak {V}_{3}$: Economic Benefits, and $\mathfrak {V}_{4}$: Enterprise Infrastructure. Each criterion is assigned a weight as a vector, such as 0.4, 0.3, 0.2, and 0.1, respectively, reflecting the expert opinions. Consequently, the ERM scheme selection process is conducted by applying the outlined methodology. To streamline the assessment, criteria $\mathfrak {V}_{1}$, $\mathfrak {V}_{2}$, $\mathfrak {V}_{3}$, and $\mathfrak {V}_{4}$ are categorized into two distinct groups, $\mathfrak {m}_1$ and $\mathfrak {m}_2$, where $\mathfrak {m}_1= \left\{ \mathfrak {V}_{1},\mathfrak {V}_{3}\right\}$ and $\mathfrak {m}_2= \left\{ \mathfrak {V}_{2},\mathfrak {V}_{4}\right\}$. Within each category, any two criteria are related, represented by $\mathfrak {v}_{1}=2$ and $\mathfrak {v}_{2}=2$.

The proposed method consists of the following stages, each contributing to the comprehensive DM process.

Step 1: The IVPF data provided by decision-makers is shown in Table 1.

Table 1 Interval Valued picture fuzzy evaluation matrix.

Step 2: As all the criteria are benefit. So, we do not need to normalize the original matrix.

Step 3: Now in Eq. (27), if we let $\delta =2$ then the aggregated values of each alternative $\mathfrak {O}_{i}(i=1,2,3,4,5)$ can be obtain as shown in Table 2.

Table 2 Aggregated values.

Step 4: Using Eq. (6), the score value of each alternatives $\mathfrak {O}_{i}(i=1,2,...5)$ can be fined as presented below: $S(\mathfrak {O}_{1})=0.4114$ , $S(\mathfrak {O}_{2})=0.2711$ ,$S(\mathfrak {O}_{3})=0.3325$ , $S(\mathfrak {O}_{4})=0.1829$,$S(\mathfrak {O}_{5})=0.2128$.

Step 5: According to the derived values, the final ranking can be determined as $\mathfrak {O}_{1}>\mathfrak {O}_{3}>\mathfrak {O}_{2}>\mathfrak {O}_{5}>\mathfrak {O}_{4}$. Thus, we get the best optimal in $\mathfrak {O}_{1}$.

The derived ranking results are shown graphicly in Fig. 2.

Fig. 2

Ranking results obtained via proposed aggregation operator.

Comparative study

In the following section, comparison analysis with other existent aggregation operators, including weighted IVPF Maclaurin symmetric mean (WIVPFMSM) operator¹⁹, weighted IVPF dual Maclaurin symmetric mean (WIVPFDMSM) operator¹⁹, weighted IVPF frank (WIVPFFA) averaging (WIVPFFA)²³ operator, weighted IVPF frank geometric(WIVPFFG)²³, weighted IVPF (WIVPFFA) averaging (WIVPFA)³⁴ operator, and weighted IVPF geometric (WIVPFG)³⁴ operator are undertaken to illustrate the benefits of the presented method. The final results of employing these aggregation operators in the preceding example are displayed in Table 3.

Table 3 Comparision with the existing aggregation operator.

Table 4 Characteristic comparison of different AOs.

Table 3 reveals that, according to all approaches, alternatives $\mathfrak {O}_{1}$ and $\mathfrak {O}_{4}$ are consistently designated as the best and worst alternatives, respectively. While the ranking orders of the remaining alternatives may vary slightly in some cases, this consistency confirms the validity of the proposed approach. Moreover, we scrutinize the reasons behind the superior performance of the developed method compared to other listed methods, as outlined below:

i). MCDM methodology¹⁹ employs the WIVPFMSM and WIVPFDMSM operators, MCDM method²³ utilizes the IVPFFWA and IVPFFWG operators, MCDM approach³⁴ incorporates the WIVPFA and WIVPFG operators, and our developed method introduces the novel WIVPHFPMSM operator. Examination of Table 3 reveals that the orderings of IVPFFWA²³, WIVPFA, and WIVPFG³⁴ operators align with the designed MCDM method based on the WIFPDMSM operator, namely $\mathfrak {O}_{1}> \mathfrak {O}_{3}>\mathfrak {O}_{2}> \mathfrak {O}_{5}>\mathfrak {O}_{4}$. However, none of these operators, including others, precisely captures the relationship structure when criteria are categorized into multiple classes. On the other hand, our proposed method considers the interrelationships within criteria belonging to the same group. In the current instance, criteria $\mathfrak {V}_{1}$ and $\mathfrak {V}_{3}$ exhibit a connection, as do criteria $\mathfrak {V}_{2}$ and $\mathfrak {V}_{4}$. Yet, there is no interrelationship between the groups $\left\{ \mathfrak {V}_{1},\mathfrak {V}_{3} \right\}$ and $\left\{ \mathfrak {V}_{2},\mathfrak {V}_{4} \right\}$. Clearly, our method, based on the introduced WIVPHFPMSM operator, effectively addresses this scenario by acknowledging the relationships within the members of the same set, thereby mitigating the influence of irrelevant members.

ii). Though the operators introduced by Ashraf et al.¹⁹ account for the relationships among criteria, they fall short in classifying criteria into distinct classes. In contrast, the proposed approach addresses this limitation. A comparison in Table 3 reveals slight variations in the sorting order of alternatives between the rankings derived by Ashraf et al.¹⁹ operators and those produced by the proposed operator. This disparity arises because the existing operators solely rely on interrelationships and do not categorize the criteria.

iii). The inclusion of $\delta$ in the proposed operators provides decision-makers with enhanced flexibility and robustness, enabling them to choose the most suitable $\delta$ in accordance with their risk preferences. Moreover, specific parameter values render several existing operators as special cases of the developed operator. This comprehensive nature empowers the developed operators to effectively address a wider range of MCDM problems.

To highlight the advantages of the proposed operators compared to others, a detailed characteristic comparison is presented in Table 4.

Besides the mentioned advantages, the designed operators have certain limitations, including:

i) The formulated operators are developed within the framework of IVPFS, which may prove inadequate in some uncertain scenarios. For instance, if we consider $\mathcal {G}=([0.2, 0.4], [0.3, 0.4], [0.1, 0.3])$, the necessary condition for IVPFS is not satisfied because $0.4 + 0.4 + 0.3 = 1.1,$ which exceeds the acceptable range.

ii) The proposed operators’ algorithm is based on predetermined criteria weights; however, this assumption does not hold true for all DM problems. In many cases, criteria weights may be unknown or partial known.

Next, we compute the Wojciech Sałabun (WS) coefficients³⁵ and the Spearman rank correlation (SRC) coefficients³⁶ between the existing AOs, WIVPFG, WIVPFA, IVPFFWG, IVPFFWA, WIVPFDMSM, and WIVPFMSM, and the proposed methodology. The WS coefficients yield 1.0000, 1.0000, 1.0000, 0.9167, 1.0000, 0.8542, and 0.9167, respectively, while the SRC coefficients yield 1.0000, 1.0000, 1.0000, 0.9, 1.0000, 0.9000, and 0.9000. These coefficients quantify both the strength and direction of the relationship between the two approaches. As depicted in Figure 3, the WS coefficients exceed, or equal 0.8542 for each established approach, and SRC WS coefficients exceed or equal 0.9000 for each established approach, demonstrating the validity of the developed methodology.

Fig. 3

Correlation plot of the proposed methodology with the existing operators.

Conclusions

The PMSM operator acknowledges grouping criteria into multiple categories, noting interrelations among criteria within each group. Leveraging these advantages, the initially proposed PMSM operator has been extended to the IVPF setting, and its weighted form has been deployed to precisely address MCDM problems. Some special cases and relevant results of these operators have been thoroughly examined. A novel MCDM framework has been established within the context of the designed WIVPFPMSM operator. This approach categorizes criteria into distinct classes, where criteria within the same class are considered interconnected, while criteria belonging to different classes are deemed independent. Finally, we presented a numerical example to illustrate the applicability of the proposed approach. The comparative analysis of the presented work demonstrates that our developed MCDM approach is more efficient than existing methods, particularly in capturing the interdependence and classification among criteria to effectively address MCDM problems in an IVPF environment. In future research, we plan to expand the application of the PMSM operator to other DM processes^37,38,39,40, risk analysis, and various other fuzzy environments.