Introduction

Low-light night vision imaging technology has been widely applied in various aspects of production and daily life and holds a crucial position. High-quality-low-light imaging has become increasingly important in military night-time surveillance, public safety monitoring, biomedical imaging, and other fields1,2,3. However, owing to the limitations of the acquisition equipment, images captured under low-light conditions are often affected by noise that makes them capture only limited visual information, significantly reducing the image quality and analysis accuracy4,5,6. Therefore, enhancing the quality of low-light images, particularly by reducing noise and restoring the image details, is increasingly significance for advancing low-light night vision technology7.

Night vision performance can be enhanced by directly using expensive night vision cameras. Additionally, physical limitations of the optical system hinder an improved hardware performance that enhances image quality8. Image-denoising technology, which restores high-quality images from noisy images captured by ordinary cameras, provides a flexible and cost-effective solution for addressing this issue9,10,11. Image denoising is a critical task in low-level computer vision, particularly under low-light conditions12. Early denoising methods were based on image self-similarity and local consistency. However, these approaches often yield suboptimal results when handling complex noisy scenes and require intricate optimization processes13,14. In recent years, significant advancements have been made in deep-learning-based denoising techniques. Particularly, methods based on convolutional neural networks (CNNs), with their outstanding ability to extract local features, are at the forefront of the image-denoising field15,16,17. However, CNNs have limitations in capturing long-range dependencies in images, which are particularly evident in complex low-light image denoising tasks16,18,19.

Transformer-based methods have recently demonstrated strong performance in image-denoising tasks, which is attributed to their self-attention mechanism in capturing global dependencies and detailed features in images20. However, these methods have some notable shortcomings when used for low-light image denoising. First, standard Transformer models rely on a global self-attention mechanism in the spatial dimension whose computational complexity increases quadratically with the number of tokens, leading to a significant increase in computational costs of processing high-resolution images21,22. Although local-window-based self-attention strategies attempt to reduce computational complexity, they cannot optimise the nonlocal self-similarity of images, thereby limiting their denoising performance under complex low-light conditions23,24,25. Second, traditional Transformer methods inadequate consider the spatial correlation of images in their channel-dimension self-attention calculations, overlooking the potential contributions of internal spatial structure information of images to denoising performance26,27. Some methodscite28,29,30 have attempted to improve the scores between similar tokens by intervening in the attention map to leverage the self-similarity characteristics of images; however, their receptive fields are limited.

We present an innovative local–global interaction Transformer (LGIT) model designed to address the high computational complexity and underutilised spatial correlation in existing Transformers for low-light image denoising. This study proposes a superpixel-guided self-attention mechanism to dynamically select the patches that are most relevant to the target patch. Based on this, a top-N patch cross attention (TPCA) module was constructed to achieve comprehensive and detailed feature extraction and noise suppression while maintaining computational efficiency. Additionally, a mixed dual-gating feedforward network (MDGFF) is introduced to further enhance the capability of the model to capture multiscale local correlations in images. The resulting LGIT employs a hierarchical encoder-decoder network architecture to effectively compute self-attention within and between patches at different scales, thereby achieving precise noise removal and detailed recovery in low-light images.

The main contributions of this study can be summarised as follows:

  1. 1.

    The proposed LGIT model resolves the high computational complexity and insufficient utilisation of image spatial correlation in low-light image denoising tasks when using Transformer-based methods.

  2. 2.

    A TPCA based on superpixel segmentation is designed, dynamically selecting the top-N patches most similar to the target patch. This achieves cross-attention aggregation in the channel dimension, effectively utilizing the non-local self-similarity of the image while reducing computational complexity.

  3. 3.

    An MDGFF is introduced to effectively extract the multi-scale local correlations of the image. This enhances the model’s ability to denoise images with large noise under low-light conditions while ensuring low computational cost and efficient information interaction.

The remainder of this paper is organised as follows. Section “Related work” introduces advancements in related research. Section “Method” details the architecture design and key technologies of the LGIT model, including the top-N patch selection module, superpixel-guided TPCA, and MDGFF. Section “Experimental results” presents the performance of LGIT on several low-light image-denoising datasets and in comparison with the current state-of-the-art methods. Finally, Section “Conclusions” summarises the main content of this study and discusses future research directions.

Related work

Low-light image denoising

  • CNN-based: CNN-based methods have made significant progress in the field of low-light image denoising. DnCNN31 is the first demonstration of deep learning technique in effectively learning noise distribution in image denoising. Subsequently, ResNet32 introduces residual learning to solve the degradation problem in deep network training. DenseNet33 significantly improves feature utilization efficiency through dense connections. Additionally, MIRNet34 utilises an encoder-decoder structure to extract multiscale features of images. OKNet35 also enhances the efficiency of image restoration by improving multi-scale representation learning, while SSAMAN36 effectively expands the receptive field of CNNs by combining adaptive pixel attention and adaptive channel attention branches. SFNet37 employs a U-Net backbone and performs image restoration through frequency selection. Additionally, SANet38 designs a spatially adaptive network to enhance the illumination of low-light images based on Retinex theory. Although these models achieve significant results in noise suppression and detail recovery, the limited receptive field of CNNs restricts their ability to fully exploit the nonlocal self-similarity of images to further enhance denoising performance.

  • Transformer-based: In recent years, these methods have gained widespread attention for image denoising owing to their excellent capability to handle global information. ViT39, the first model to apply Transformers in computer vision, demonstrated the potential of self-attention mechanisms for extracting global features of images. Subsequently, IPT40 uses global attention to aggregate information from all spatial positions into a target token for specific image-denoising tasks, with computational complexity squared by image resolution. Variants such as SwinIR41 and Uformer42 introduce local windows and U-shaped network structures to reduce the computational complexity of Transformers in image restoration tasks. Restormer26 uses channel attention instead of local window attention within a U-shaped network structure to achieve efficient computation in large-scale image restoration tasks. PCformer43 enhances image processing by capturing local context and global dependencies using an encoder-decoder architecture. Methods such as Xformer44 and HAT45 combine local window and channel attention to address both local and global image information. EfficientViT46 employs lightweight multi-scale representations for feature extraction, thereby reducing the computational complexity of the model. Despite their excellent performance in extracting global dependencies and handling denoising tasks in complex scenarios, these models still struggle with high computational complexity and adaptability to specific noise patterns in low-light image denoising15,47.

Superpixels-based attention mechanism

Superpixel-based attention mechanisms provide a new perspective for image denoising, particularly for handling low-light-noise images. Superpixels aggregate similar pixels to form larger pixel blocks, thereby reducing image complexity while preserving important structures and information. This method enhances the computational efficiency of subsequent processing steps and ensures superior image quality.

Recent studies21,48,49 have begun to explore the combination of superpixels and attention mechanisms to improve image denoising performance. Using the structural information of superpixels to guide the focus areas of the attention model, critical image information under low-light conditions can be processed more effectively. For example, by analysing the superpixel structure, the attention mechanism can more accurately locate regions related to the target pixels, thereby prioritising these areas to enhance denoising performance.

In specific applications of low-light image denoising48, superpixel-based attention mechanisms can effectively reduce noise interference, while improving the ability to restore image details. This is because superpixels reduce the computational burden and provide more precise guidance information for the attention mechanism, enabling it to better recognise and process noise and signals within the image. Further research21 has explored optimising the superpixel generation process and designing attention models to further enhance the image restoration effects, demonstrating great application potential.

Superpixel-based attention mechanisms offer a new perspective for low-light image denoising by segmenting images into intrinsically similar superpixel blocks. The core advantage of this method lies in its ability to focus attention calculations on highly correlated regions, effectively reducing the computational complexity without sacrificing the utilisation of global image information50,51,52. This refined attention-focusing strategy allowed the model to capture and fully utilise the structural information of the image while maintaining low computational costs, thereby achieving more precise noise suppression and image restoration under low-light conditions.

Although superpixel segmentation provides an efficient structured representation of the image, effectively combining these segmentation results with attention calculations to enhance the denoising performance remains a primary challenge. Current research has not yet fully explored the guiding role of superpixel segmentation in attention mechanisms, particularly in the utilization of structural information of superpixels to optimise attention focus areas. This would enable a more accurate use of both global and local information in low-light images for denoising while maintaining computational efficiency.

Method

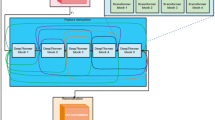
Overview

Figure 1a illustrates the overall structure of LGIT. After receiving a degraded image, the top-N patch-selective module (TPSM) was applied. This module segments the original image into superpixels based on texture and colour, and assigns each pixel with high similarity to a superpixel region. It then calculates the most relevant top-N patch information at different scales for each patch. Subsequently, the output of TPSM, along with the degraded image, is fed into a U-shaped network composed of multiple patch-selective attention (PSA) Transformer blocks at different scales for image noise extraction. As shown in Fig. 1b, each PSA block contains a TPCA mechanism that aggregates the information of the top-N patches into the target patch, window-based self-attention (WSA), and MDGFF.

Fig. 1
figure 1

Architecture of LGIT for low-light image denoising. (a) Architecture of the proposed local–global interaction Transformer (LGIT). (b) PSA Transformer Block.

Full size image

Before feeding the degraded image into the U-shaped network, a 3 × 3 convolution is employed to embed the original noisy image \({I_{noise}}\) into a high-dimensional feature space. Subsequently, the input \({x_0}\) to the deep feature extraction module is obtained as follows:

$$\begin{aligned} \begin{array}{c} x_0 = f_{{\textrm{embed}}}(I_{noise}) \\ \end{array} \end{aligned}$$
(1)

The proposed LGIT employs a U-shaped hierarchical network architecture that is capable of preserving and integrating features at different scales. The model enhances its ability to transfer and fuse features by introducing skip connections between the upsampling and downsampling stages. The input feature map \({x_0}\) was first progressively compressed through 4 downsampling levels, with each downsampling level doubling the number of feature map channels and halving the spatial dimensions. For example, at the first level, the feature map is transformed from \({x_0} \in {R^{C \times {\textrm{H}} \times {\textrm{W}}}}\) to \({x_1} \in {R^{2C \times \frac{\textrm{H}}{2} \times \frac{\textrm{W}}{2}}}\). After passing through all 4 downsampling levels, the feature map reaches its smallest spatial scale, at which point a bottleneck stage is introduced to capture dependencies across a larger spatial range.

During the upsampling stage, the feature maps were reconstructed using k-decoders. Before each decoder, the feature maps were upsampled, doubling their spatial dimensions and halving the number of channels. After upsampling, a 1 × 1 convolution is applied to fuse the feature maps transmitted by skip connections with the feature maps of the current layer in the channel dimension.

The encoding and decoding processes of LGIT consist of PSA Transformer blocks. In PSA, TPCA identifies the top-N most relevant patches for each patch based on superpixel segmentation results, effectively supporting the precise recovery of local details. In the final stage of the network, a 3 × 3 convolution is employed for further refinement of the feature map, generating the noise residual image \({\textrm{R}} \in {R^{{\textrm{H}} \times {\textrm{W}} \times {\textrm{3}}}}\). The restored image is then calculated as \({I_{{\textrm{output}}}} = {I_{noise}} + {\textrm{R}}\).

Top-N patches selective module

We propose TPSM to calculate the most relevant top-N patches for each patch at different scales based on superpixel segmentation results. Unlike traditional methods that limit the attention computation within regular patches to reduce the computational complexity of Transformers, we utilise the output of TPSM to compute the cross-attention between the target patch and its most relevant top-N patches. This approach leverages non-local self-similar patches in an image to improve the target patch recovery.

Specifically, during the superpixel segmentation stage, the soft k-means-based superpixel segmentation algorithm from SPIN21 was first applied to the input image, yielding the initial superpixel segmentation results \(S_0\). Afterward, using the proposed hard-association-based merging strategy, the superpixel regions in \(S_0\) were merged to form larger and more meaningful superpixel regions. In this step, the colour and spatial properties of each superpixel region were evaluated, and adjacent small superpixel regions with similar colours were merged into larger regions. The merging algorithm is:

$$\begin{aligned} \begin{array}{c} {\mathrm {if\ }}{c_i} - {c_j}< \theta {\mathrm {\ and\ dist}}({s_i},{s_j}) < \phi \ {\mathrm { then\ merge}} \end{array} \end{aligned}$$
(2)

where \({c_{\textrm{i}}}\) and \({c_{\textrm{j}}}\) are the colour centres of superpixel regions \({\textrm{i}}\) and \({\textrm{j}}\), respectively; and \(\theta\) and \(\phi\) represent the colour and spatial merging thresholds, respectively. The spatial distance \({\textrm{dist}}({s_i},{s_j})\) between the centroids of superpixel regions i and j is calculated using the Euclidean distance:

$$\begin{aligned} \begin{array}{c} {\textrm{dist}(s_i, s_j) = \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}} \end{array} \end{aligned}$$
(3)

where \((x_i, y_i)\) and \((x_j, y_j)\) are the coordinates of the centroids of superpixel regions i and j.

Subsequently, the differentiable label information of the SLIC algorithm is used to perform fine patch mapping on the feature maps at different scales. The core of this step is to map the patches divided by the PSA to the superpixel region where their internal pixels occupy the highest proportion. This ensures that each patch mapped to the superpixel region that covers the largest area. Finally, the top-N-related patches for each patch at different scales were computed using the consistency of the superpixel regions to select related patches, ensuring the compatibility and coherence of features between patches.

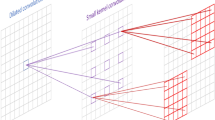
In TPSM, the input image is first subjected to superpixel segmentation and hard-association-based merging. Subsequently, patch mapping was performed based on the sizes of the feature maps and patch divisions at different scales. Finally, the top N-related patches are computed for each patch. Figure 2 illustrates TPSM, and Fig. 2c shows the final result. In the figure, four patches are selected, and the arrows indicate the selected top-N (N=7) patches for each corresponding patch.

Fig. 2
figure 2

The Top-N Patches Selective Module (TPSM) of our method, which incorporates Superpixel segmentation, Hard-association-based merging, Patch mapping, and Top-N patches calculation steps.

Full size image

Top-N patches cross attention

Low-light noisy images often exhibit significant nonlocal self-similarity, which is a valuable prior knowledge for image denoising. In existing image-restoration methods, although traditional Transformer architectures are capable of handling global information, they have a prohibitively high computational complexity owing to their global self-attention mechanism when processing high-resolution images. Local window-based methods reduce computational complexity, but still require improvement in adapting to specific noise patterns and leveraging nonlocal self-similarity when dealing with low-light images. Channel-based Transformer architectures, such as Restormer26, excel at capturing the global dependencies of features. However, these methods rely on intricately designed deep-feature interactions and complex channel attention mechanisms, which can be insufficiently sensitive to local contextual details, particularly when fine textures or structures are present in an image.

To achieve better denoising performance, we adopted a superpixel segmentation-guided deep feature extraction algorithm, aggregating highly similar patches in the image to fully utilise the redundancy of these self-similar patches. We propose superpixel segmentation-guided TPCA. This model introduces superpixel segmentation as prior knowledge and employs a novel approach that overcomes the high computational cost of global self-attention while optimising the limitations of channel attention methods in capturing local details. TPCA uses the results of superpixel segmentation to guide the attention mechanism and performs self-attention calculations between the target patch and its most relevant top-N patches, thereby significantly reducing computational complexity. This method first obtains information regarding the target patch and its most relevant top-N patches using a superpixel segmentation module. Cross-attention is then applied to each target patch, where the query vector (Q) is generated by the target patch and keys (K), and the values (V) are generated by feature maps aggregated from the top-N patches most relevant to the target patch along the channel dimension. This approach effectively utilises the global contextual information of an image while maintaining computational efficiency and precisely restoring the image details.

TPCA principally and efficiently transforms feature maps segmented by superpixels into new representations with enhanced contextual information during the encoding and decoding stages. For example, consider the first TPCA in the encoding stage. The input was a five-dimensional tensor processed by a superpixel segmentation module structured as [256, 7, 8, 8, 32]. Here, 256 represents the number of patches resulting from segmenting the original 128 × 128-sized input feature map; that is, the window size of patches during \({\mathrm {M = 8}}\). The number 7 denotes the seven patches most relevant to the target patch, including the target patch. The subsequent three dimensions [8, 8, 32] correspond to the spatial size and channel number of each patch.

Fig. 3
figure 3

The proposed Top-N Patches Cross Attention (TPCA) module. We propagate information from Top-N patches to target patch by cross attention mechanisms.

Full size image

As shown in Fig. 3, in the TPCA, the feature map of the target patch \(t \in \mathbb {R}^{M \times M \times C}\), assuming an embedding dimension of D, was transformed into a query matrix \(Q^{t} \in \mathbb {R}^{C \times D}\) through a linear projection. Similarly, the feature map \(x \in \mathbb {R}^{M \times M \times NC}\) from the top-N patches generates the key matrix \(K^{x} \in \mathbb {R}^{NC \times D}\) and the value matrix \(V^{x} \in \mathbb {R}^{NC \times M^2}\) (Eq. 4). Through this process, the contextual information from the top-N patches is effectively transmitted to the target patch, achieving feature enhancement and enrichment. The linear transformations used in this process are represented by the weight matrices \(W_{q}^{t} \in \mathbb {R}^{M^2 \times D}\), \(W_{k}^{x} \in \mathbb {R}^{M^2 \times D}\), and \(W_{v}^{x} \in \mathbb {R}^{M^2 \times M^2}\), which are used to compute Q, K, and V, respectively. Through the computation of cross-attention, the network can focus on the patch information most relevant to the target patch without having to pay attention to other irrelevant feature regions, greatly improving computational efficiency and capturing local structures and details in the image more accurately.

$$\begin{aligned} \begin{array}{c} {Q^{\textrm{t}}} = {\textrm{t}}W_q^{\textrm{t}},\quad {K^{\textrm{x}}} = xW_{\textrm{k}}^{\textrm{x}},\quad {V^{\textrm{x}}} = xW_v^{\textrm{x}} \end{array} \end{aligned}$$
(4)

Subsequently, attention scores, which reflected the similarity between the target patch and each of the top-N patches, were obtained by calculating the dot product of Q and K and then normalizing them. The calculated attention scores guided the transfer of information from the top-N patches to the target patch. The computational process is expressed as

$$\begin{aligned} \begin{array}{c} {\mathrm {Attention\ Scores}} = {\textrm{softmax}}\left( {\frac{{Q{K^T}}}{{\sqrt{D} }}} \right) \end{array} \end{aligned}$$
(5)

The attention scores are multiplied by the value vector V to obtain an updated feature representation of the target patch. The final output calculation process can be expressed as

$$\begin{aligned} \begin{array}{c} {\mathrm {Attention\ Output}} = {\textrm{softmax}}\left( {\frac{{Q{K^T}}}{{\sqrt{D} }}} \right) {\textrm{V}} \end{array} \end{aligned}$$
(6)

Through this cross-attention mechanism, TPCA can effectively integrate information from globally relevant patches into the target patch, which not only improves the feature expression ability but also maintains high computational efficiency.

Mixed dual-gating feedforward network

In the TPCA, following the Self-Attention (SA) module, we propose a novel MDGFF module to improve the information flow efficiency and feature expression capabilities by introducing mixed-scale and dual-gated mechanisms.

As shown in Fig. 4, MDGFF first applies Layer Normalization to the input features and then processes these features through two parallel-gated convolutional paths. These two paths were designed at different scales to aggregate multi-scale contextual information. Specifically, path P1 uses 1\(\times\)1 and 3 × 3 convolutions whereas path P2 uses 1 × 1 and 5 × 5 convolutions. This design aims to expand the receptive field of the model while maintaining a manageable computational complexity.

After the convolution operation, the features on the two paths were separately transformed nonlinearly by the ReLU activation function and subjected to feature selection by a gate unit (G). The role of the gate unit is to learn how to select and integrate information from parallel paths to enhance the expressive ability of a network. Mathematically, the gate operation can be expressed as:

$$\begin{aligned} \begin{array}{c} G = \sigma ({\textrm{Conv}}(F)) \end{array} \end{aligned}$$
(7)

where F represents the feature before the gate, \(\sigma\) is the sigmoid function used to generate weight coefficients between 0 and 1, and Conv represents the convolution operation. The weight coefficient generated by the gate is multiplied by the feature for selective enhancement.

Fig. 4
figure 4

The conceptual illustration of the proposed Mixed-scale Dual Gated Feed-Forward Network (MDGFF).

Full size image

The outputs of the two paths are then merged and passed through a 1 × 1 convolution to integrate the information. The final output feature is expressed by the following equation:

$$\begin{aligned} \begin{array}{c} {{\textrm{F}}_{{\textrm{out}}}} = {\textrm{Con}}{{\textrm{v}}_{1 \times 1}}(G{F_{P1}} + (1 - G){F_{{\textrm{P2}}}}) \end{array} \end{aligned}$$
(8)

where \({F_{out}}\) represents the output feature of the MDGFF, whereas \({F_{P1}}\) and \({F_{P1}}\) represent the processed features from the two paths. Ultimately, this output feature is combined with the output of the self-attention module and returned to the main flow of the Transformer Block through the residual connections, thereby completing the entire process of feature extraction and enhancement.

By incorporating the MDGFF module, the model can capture and utilise features at different scales more comprehensively, thereby providing stronger support for image denoising and detail recovery and restoration. This design of the multiscale feedforward network enhances feature representation and ensures the computational efficiency of the entire network.

WSA calculates the self-attention within each patch individually, effectively handling the local features of the image. This allowed the model to analyse the details of each region more accurately. The standard WSA from Uformer42 was employed to process the patches. Ultimately, the complete PSA is formed by concatenating a cross-attention mechanism that aggregates the top-N patch information into the target patch (TPCA + MDGFF) and the WSA + MDGFF.

Experimental results

This section discusses the implementation details. It then validates the effectiveness and efficiency of the LGIT method on the SIDD and DND datasets. Finally, an analysis from a comprehensive ablation experiment to verify the effectiveness of each component of the LGIT is presented.

Implementation details

This study selected SIDD53, a dataset specifically designed for image-denoising research, as the training set. SIDD employs five representative smartphones to capture 30,000 noisy images from ten different scenes. To test the performance of the algorithm, we utilised the test sets of the SIDD and DND datasets. The Darmstadt noise dataset (DND)54 was specifically tailored for image denoising research. It was released by Darmstadt University of Technology and aims to provide real-world noisy images and their corresponding clean image pairs for evaluating image-denoising algorithms.

In this experiment, the AdamW optimiser was used, with \({\beta _1}\) set to 0.9, and \({\beta _2}\) set to 0.999. The training data underwent random rotations of 90°, 180°, and 270° and horizontal flipping for data augmentation. A cosine decay strategy is employed, reducing the learning rate from an initial value of 2e-4 to 1e-6. The patch size of LGIT was set as 8 × 8. Charbonnier loss55 was used to train the LGIT. The number of PSA blocks per layer (N1-N4) in the network is set to 1, 2, 8, 2. The PyTorch deep learning framework was used, and training was conducted on NVIDIA V100 GPUs, achieving convergence after 200 epochs.

Following related works on image denoising tasks26,42, the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measurement (SSIM) were used as evaluation metrics. The images were converted from the RGB colour space to the YCbCr colour space, and evaluations were performed on the Y channel (luminance component). This is because the Y channel had a more significant impact on the perceived visual quality of the human eye, making it more effective at reflecting the results of image denoising. For consistency, all competing methods were evaluated on the Y channel.

Fig. 5
figure 5

Visual comparisons with state-of-the-art methods on low-light image noise removal task.These methods are evaluated on images from the SIDD (top sample) and DND (bottom sample), which provide real-world noisy images captured under low-light conditions.

Full size image

Comparison with other state-of-the-art methods

In this section, the proposed method is compared with other SOTA image-denoising algorithms, including traditional methods such as BM3D14 and CNN-based methods such as DnCNN31, CBDNet56, CycleISP57, AINNet58, and DeamNet59, as well as Transformer-based models such as Uformer42, PCformer43, Restormer26, and Xformer44.

Table 1 The quantitative comparisons results on SIDD53 and DND54 datasets
Full size table

The quantitative metrics of the different methods are listed in Table 1. Overall, Transformer-based models outperform CNN-based methods in terms of PSNR and SSIM. This superiority can be attributed to the stronger global information modelling capability of Transformers compared with CNNs. Through their self-attention mechanism, Transformers effectively capture dependencies between pixels, allowing them to establish broader connections across different parts of the image. This enhances the overall understanding and processing of image content.

However, to reduce computational complexity, some Transformer-based methods restrict attention to regular patches41,42 or across feature map channels26. These approaches fail to fully leverage the nonlocal self-similarity properties of images.

In comparison, the method proposed in this study uses superpixel guidance to aggregate patches with high relevance, thereby achieving finer local information processing, while maintaining sensitivity to global content. Through this approach, LGIT can retain the utilization of global image features while maintaining low computational complexity and effectively removing noise, especially in image details and texture. The superpixel-guided aggregation strategy optimises the information integration process, resulting in richer and more relevant information being extracted from each patch, which directly improves the denoising performance.

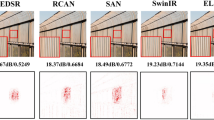
Figure 5 shows the denoising performance of several methods on the SIDD and DND datasets. The results show that when superpixel regions are evident in the image and the image exhibits strong nonlocal self-similarity characteristics, the proposed LGIT method can effectively restore noise-contaminated regions. In contrast, methods that limit attention within patches cannot utilise information from other patches similar to the target patch, and thus fail to achieve good denoising performance. As can be clearly seen from the figure, the denoising performance of our method is superior to that of the other methods, further demonstrating the important role of utilizing nonlocal self-similarity in low-light image denoising.

Ablation study

This section analyses the design of the LGIT model and the effectiveness of its key components. All ablation studies were conducted under the same conditions to ensure the fairness of the experiments.

Table 2 The effect of the key components in our LGIT
Full size table

Effectiveness of Top-N patches cross attention (TPCA)

The TPCA module is a core component of the LGIT. Through the cross-attention mechanism, the TPCA aggregates information from patches within the same superpixel region into the target patch, thereby effectively denoising the image. We integrated TPCA into different layers of the U-Net backbone and present performance comparisons under different settings in Table 2. These results indicate that the absence of the TPCA leads to a performance drop because the use of self-attention (WSA) alone fails to capture sufficient long-range information. As TPCA is integrated into more layers, the network performance gradually improves.

Additionally, we experimented using only the TPCA and removing the WSA and found that this approach performed slightly worse than using the WSA alone. This confirms the necessity of leveraging both the local properties and nonlocal self-similarity in image denoising. We also conducted ablation studies on the selection of “Top-N,” and the PSNR performance for different values of “Top-N” is shown in Fig. 6a. It can be observed that setting “Top-N” to a smaller value leads to performance degradation due to insufficient relevant patch information for target patch recovery, whereas an excessively large “Top-N” value introduces interference from irrelevant patches, also leading to performance decline.

To effectively evaluate the model, Table 2 presents a comparison of the model parameter counts under different settings. The results show that LGIT has a model parameter count of 60.12M. Compared to Uformer (50.88M), LGIT, with an increase of only 9.24M parameters, achieves a PSNR improvement of 0.51 dB (40.40 dB vs. 39.89 dB). Additionally, LGIT achieves a FLOPs count of 189.11G, which is higher than Restormer’s 155G. Despite this higher computational cost, LGIT provides a PSNR improvement of 0.38 dB (40.40 dB vs. 40.02 dB), demonstrating its superior performance. Compared with ViT-Base (with 86M parameters) and ViT-Large (with 307M parameters)39, which rely on a global self-attention mechanism, LGIT significantly reduces the number of parameters to 60.12M by incorporating a superpixel-guided global self-attention mechanism. Overall, LGIT achieves SOTA performance while maintaining computational efficiency comparable to patch-based and channel-based methods, thereby significantly reducing the parameter count relative to global self-attention methods.

Fig. 6
figure 6

Ablation study results. (a) Ablation analysis of different values of Top-N. (b) Ablation analysis of different values of patch size.

Full size image

Influence of patch size on network performance

As shown in Fig. 6b, when the patch size is 8, the model’s PSNR reaches its peak, outperforming patch sizes of 4 and 16 by 0.77 dB and 1.45 dB, respectively. This indicates that a medium-sized patch can effectively capture sufficient contextual information while maintaining low computational complexity, thereby optimizing image restoration quality. In contrast, although smaller patch sizes reduce computational complexity, they limit the model’s ability to capture the necessary contextual information, thus affecting performance. Larger patch sizes, while covering a broader context, increase computational complexity and may introduce excessive irrelevant information, negatively affecting the denoising effectiveness of the model.

Fig. 7
figure 7

Ablation study of MDGFF module.

Full size image

Effectiveness of mixed-scale dual-gated feed-forward network (MDGFF)

The ablation experiment results (Table 3) demonstrate that MDGFF improves PSNR by 0.05 dB compared to the standard Feed-forward Network (FFN), proving the effectiveness of the dual-gating mechanism and mixed-scale design. Furthermore, experiments using single-scale feed-forward networks reveal that their performance drops by 0.03–0.04 dB compared to the mixed-scale MDGFF, further validating the advantage of the mixed-scale approach in capturing multi-level feature information.

Figure 7 shows a PSNR performance comparison when the MDGFF module was applied to the Uformer, Restormer, and LGIT methods. The results indicate notable improvements after replacing the original FFN with the MDGFF module: Restormer’s PSNR increases from 40.02 to 40.05 dB, Uformer from 39.89 to 39.93 dB, and LGIT from 40.35 to 40.40 dB. These enhancements underscore the significant performance improvement in image reconstruction achieved by the MDGFF module.

Table 3 Ablation study of Feed-forward Network.
Full size table

Comparison of the impact of different input data types on denoising performance

The SIDD dataset includes both PNG (sRGB) and RAW data types. Images were categorized into three lighting conditions: low light, normal brightness, and high exposure. Table 4 compares the results of training models using these two types of input data, with all other training parameters held constant. The experimental results show that models trained on RAW data perform better. This is because sRGB images undergo nonlinear transformations during the ISP process, complicating noise modeling. By contrast, RAW data-which are uncompressed, have higher bit depth (12-bit or more), and have not been subjected to ISP nonlinear processing-offer greater flexibility for deep learning-based noise removal.

Testing across the three lighting conditions shows that the advantage of using RAW data is most pronounced under low light. This is because noise is more prominent and the overall image is darker in low-light conditions, causing loss of information concentrated in lower pixel values when using sRGB data. Therefore, training with RAW images better enables the network to map noisy images to clean ones compared to sRGB images.

Table 4 Comparison of denoising performance between sRGB and RAW input data formats under different lighting conditions.
Full size table

Conclusions

We propose a novel model called LGIT, which integrates TPCA with superpixel segmentation and an MDGFF. This model addresses the challenges of high computational complexity and insufficient utilisation of spatial correlation during low-light image denoising.

LGIT effectively captures nonlocal self-similarity and detailed information in low-light noisy images through a sophisticated global interaction strategy. Extensive experiments indicate that LGIT outperforms existing SOTA methods on several low-light image-denoising benchmark datasets, validating its effectiveness and efficiency in practical applications. Despite achieving decent performance, the model’s dependency on superpixel segmentation results may lead to suboptimal performance in images with complex scenes or challenging lighting conditions. Future work could focus on enhancing the robustness of the superpixel segmentation algorithm and developing adaptive strategies to filter out irrelevant regions during self-attention computation.