Introduction

In the recent years, major efforts of different international research and development (R&D) groups in the pharmaceutical industry have been focused on the development of novel, efficacious and affordable therapeutic drugs with optimum safety, minimum side effects and acceptable biological/physicochemical characteristics1,2. Because of the availability of great numbers of active pharmaceutical ingredients (APIs) in solid state, one of the traditional drugs processing techniques is based on their recrystallization applying organic solvents as reaction media3. Despite the prevalence of application, the emergence of some drawbacks like environmental detriments, toxicity during application and wide particle size distribution has significantly restricted the use of organic solvents in drug industry4,5. To mitigate the negative effects of organic solvents, Supercritical fluids (SCFs) have been welcomed at different scientific areas such as solid drugs’ extraction and nanonization of solid dosage forms6,7,8. Industrial-based use of SCFs (especially SCCO2) is due to their precious advantages such as great potential of application in harsh operational conditions, eco-friendliness and proper efficiency9,10. SCCO2 occurs at the pressures/temperatures higher than the critical point of CO2, which causes its properties to be between the liquid state and gas state11,12,13. SCFs have indicated great capabilities in various fields including extraction, food science, nanotechnology, and drug preparation14,15,16,17.

Recently, optimization of mathematical models to determine the solubility of various kind of drugs is one of the important tasks of scientists to estimate the behavior of drug release at different temperatures and pressures18,19,20. Letrozole (Femara®) with the chemical formulation of C17H11N5 is a well-known anti-neoplastic orally-administered drug, which is extensively applied to the second-line treatment of women suffering from certain types of breast cancer21,22.

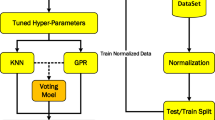
Machine learning (ML) has garnered significant momentum across various scientific disciplines, gradually supplanting traditional computing methods in an ever-expanding array of scientific domains by assuming their functionalities23. Here, we used machine learning methods to estimate solubility of LET drug. The employed models are RF (Random Forest), PAR (Passive Aggressive Regression), and RBF-SVM (Support Vector Machine with RBF kernel). Passive Aggressive Regression (PAR) is among the models used in this study that belongs to online learning approach. Unlike batch learning techniques, which develops the estimator by training on the full training data simultaneously, online machine learning allows the best predictor for future data to be updated at each step as new data becomes available24. In the ensemble learning model Random Forest (RF), voting is employed to improve the efficacy of learners featuring diverse base trees25. A random forest is popular because it predicts numerous events with minimal parameters. This approach can handle both a high-dimensional feature space and tiny examples accurately. They could handle big systems in the real world because they are parallelizable26. Support SVMs are well-known supervised models that can be used for both classification and regression tasks. Because processing takes time, it is used for smaller data sets. This method is based on the idea of finding a hyperplane that best separates inputs in distinct locations27,28,29. Here we used SVM model with the RBF kernel (RBF-SVM). These models optimized in terms of their hyper-parameters using GA algorithm as an innovation. The purpose of the current research article is to optimize three novel approaches (PAR, RF RBF-SVM) using artificial intelligence technique to estimate and develop the solubility value of Letrozole anti-cancer drug through the SCCO2. The models and their combination with optimizer (GA algorithm) are developed and implemented for the first time to correlate solubility data of Letrozole.

Data set for machine learning computing

For this work, there are 45 rows of data about LET (Letrozole) drug solubility that can be split down as follows: The inputs consist of numerical values, and the resulting output is likewise a numerical value. The data used in this investigation, which was acquired from references, is shown in Table 130. All data analytics and fitting in this study are performed using Python software.

Table 1 Used data for intelligence computing30.
Full size table

Methodology of intelligence computing

PAR (passive aggressive regression) method

To train a machine learning model online, we feed it instances one at a time or in small batches known as mini batch. As a result, problems with continuously streaming data are well-suited to the passive-aggressive approach31. Although this model is often employed for use in large-scale tasks, it can be used to much smaller data sets and still shows remarkable robustness. Passive aggressive regressors are similar to Perceptron when a learning rate is not needed. They differ from the Perceptron in that they have a regularization parameter C32,33. Classification with the squared hinge or raw hinge loss functions, and regression with the insensitive or squared insensitive loss functions, are all possible with this model as defined here31:

$$L = \left\{ {\begin{array}{*{20}l} 0 \hfill & {if\left| {y_{i} - \mathop y\limits^{{}} _{i} } \right| - \varepsilon \le 0} \hfill \\ {\left| {y_{i} - \mathop y\limits^{{}} _{i} } \right| - \varepsilon } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

Random forest

The Random Forest (RF) method combines the results of numerous Decision Tree (DT) models to approximate the desired value for a set of data points34,35. Upon receiving an input data point containing attribute values, like x, the Random Forest algorithm develops K individual trees and then computes the average of their outputs to generate a final prediction. Following is the formula for the RF model with K trees T(x)26.

$$\hat{f}_{{rf}}^{K} \left( x \right) = \frac{1}{K}\mathop \sum \limits_{{k = 1}}^{K} T\left( x \right)$$

Random Forest utilizes bagging method to enhance the diversity of the decision tree model, enabling them to be developed based on varied training set. Using the method, the entire training dataset undergoes random resampling, and the replacement data is retained. Consequently, specific data may undergo frequent utilization, while others might be employed only once. This particular strategy enhances the precision of predictions and enhances overall stability by demonstrating increased resilience to minor fluctuations in input data. In contrast, trees generated by RF use a randomly selected subset of features to determine the optimal design. This approach diminishes the overall strength of the forest, concurrently reducing the correlation among individual trees and thereby minimizing generalization error. Furthermore, as they develop, RF estimator trees do not need to be clipped, making them more computationally efficient34,36,37. Also, the out-of-bag subset is generated as an independent subset, commonly referred to as OOB. It comprises samples from the bagging process that were not picked for training the k-th tree. The kth tree can measure performance based on these OOB elements38,39.

Support vector machine (SVM) with RBF Kernel

In the SVM method, independent variable x aids in the estimation of the dependent variable y, according to40. Like in other regression scenarios, the given function determined the correlation between x and y41.

$${\text{f}}\left( {\text{x}} \right) = {\text{f}}\left( {\text{x}} \right).{\text{wT}}.\upphi \left( {\text{x}} \right) + {\text{b}}$$
$$\:\text{f}\left(\text{y}\right)=\text{f}\left(\text{x}\right)+\text{noise}$$

In recent equations, Ø stands for a kernel that accepts input data and transforms it into the required shape. SVM methods use various types of kernel functions. Polynomial, linear, sigmoid, and RBF are some examples (Here the RBF is used). w is the vector coefficient, b is a constant, and b and w are the regression function constraints. Error tolerance, on the other hand, creates noise (e). During the Support Vector Machine model’s training, Consecutive minimization association process of the error function can be obtained. Based on the error function, there are two types of SVM models: e-SVM and t-SVM42.

The RBF function is defined as43:

$$\:K(x,{x}_{i})=exp\left(\frac{-|x-{x}_{i}{|}^{2}}{{\sigma\:}^{2}}\right)$$

This function was used as a kernel in this study.

Results and discussions

As highlighted in the introduction, the introduced models have been developed through the help of genetic algorithm and the final statistical results of these models are displayed in Table 2. Based on this table, the best model is clearly the RBF-SVM model, and the RF model is on the second rank, and the PAR model is in the third place with acceptable air performance.

Table 2 Final model results.
Full size table

Figures 1, 2 and 3 also confirm this fact. In these figures, the experimental values have been checked with the values predicted by the models. In these three figures, there is a Y = X line, which represents the experimental data. The blue points illustrate the estimated values in the training and the red crosses are the predicted solubilities of test subset.

Fig. 1
figure 1

Predicted vs. observed data (PAR approach).

Full size image
Fig. 2
figure 2

Predicted vs. observed data (RF approach).

Full size image
Fig. 3
figure 3

Predicted vs. observed data (RBF-SVM approach).

Full size image

Although the RBF-SVM model was chosen as the best model and other analyzes were performed based on this model, but due to the acceptable performance of all three models, Figs. 4, 5 and 6 showcase the decision level diagrams in a three-dimensional format for each of the three models. As presented, the solubility value of Letrozole improves as the pressure does. It can be attributed to this fact that the increment of pressure increases the CO2 and thus, the solvent power improves. Increment of solvation strength takes place due to the decrement of intermolecular distance and as the result, enhancement of solute–solvent interactions. The impact of temperature on the solubility behavior is more complex. Based on the results, at the pressures greater than the cross over pressure, the positive impact of vapor pressure increment is higher than the destructive effect of solvent density decrement. Moreover, an enhancement of T at these points improves the solubility of Letrozole. For the points less than the cross over pressure, the negative effect of decreasing in density overcomes the positive influence of vapor pressure increment44. Therefore, an enhancement in temperature declines the Letrozole solubility.

Fig. 4
figure 4

Prediction 3D surface (PAR MODEL).

Full size image
Fig. 5
figure 5

Prediction 3D surface (RF MODEL).

Full size image
Fig. 6
figure 6

Prediction 3D surface (RBF-SVM MODEL).

Full size image

As mentioned before, the RBF-SVM model has the best performance among these three models. Figure 7, which shows the residual of this model, also confirms the good efficiency of this approach. In addition, the RF approach has the second performance by a short distance, so Fig. 8 also shows the importance of the features with the help of the Random Forest model. Finally, the influence of individual features on the solubility are illustrated in Figs. 9 and 10.

Fig. 7
figure 7

Final residuals of RBF-SVM model.

Full size image
Fig. 8
figure 8

Feature importance using RF.

Full size image
Fig. 9
figure 9

Impact of pressure on solubility at various temperature.

Full size image
Fig. 10
figure 10

Impact of temperature on solubility at various Pressure.

Full size image

Conclusion

Development of promising techniques to improve the solubility, dissolution ratio and bioavailability of oral-dosage chemotherapeutic medicines is still a challenge in the drug manufacturing industry. To reach these purposes, some predictive models should be developed to precisely optimize the drug solubility. In this research article, ML-based predictive models were employed to develop the solubility value of Letrozole anti-cancer drug through the SCCO2 at different ranges of pressure and temperatures. The employed models are PAR (Passive Aggressive Regression), RF (Random Forest), and RBF-SVM (Support Vector Machine with RBF kernel). The GA algorithm was used to optimize these models’ hyper-parameters. The coefficients of determination (R2) for the optimized PAR, RF, and RBF-SVM approaches are 0.8277, 0.9534, and 0.9947. In addition, the models’ MSE error rates are 0.1342, 0.0305, and 0.0045, in that order. The validated outputs exhibited that the optimized RBF-SVM approach is the best fit for this research. Using this model, the maximum prediction error is 0.1289.