Introduction

The rapid advancement of wireless communication and mobile networks within embedded systems has led to significant challenges in managing increasing data flows, emerging applications, and communication security requirements. These challenges are particularly pronounced in multimedia computer communication technologies, which serve as public-oriented information exchange platforms. Such systems necessitate robust mutual authentication processes among users, devices, and embedded systems to ensure secure communication. Despite advancements, many security issues remain inadequately addressed, highlighting the urgent need for a secure and reliable multimedia communication environment to safeguard the efficiency and security of information transmission1,2,3.

The emergence of 5G technology has garnered considerable attention due to its low latency and high-speed capabilities. Among the promising technologies for 5G, Device-to-Device (D2D) communication stands out for its ability to enable direct communication between adjacent devices, bypassing the base station4. This direct communication can significantly reduce the load on base stations and alleviate network congestion, thereby enhancing network capacity and improving the transmission performance for other users not engaged in D2D communication5. Moreover, D2D users can efficiently reuse spectrum resources allocated to the central unit (CU), further optimizing spectrum utilization3. As a load-balancing mechanism, D2D communication can offload peak traffic to nearby micro base stations with the aid of relays, providing higher data transmission rates in dense heterogeneous networks without requiring additional spectrum6.

Ensuring security in 7,8D2D communication scenarios is essential, particularly when transmitting personal or sensitive information. Although D2D links provide direct point-to-point connections and efficient spectrum utilization, they also introduce significant security challenges that need to be addressed. To enhance communication security in embedded systems and multimedia computer communications, this paper proposes a novel resource allocation scheme.

The primary goal of the proposed scheme is to optimize9,10 the security and efficiency of communication resources. Specifically, the scheme focuses on two main aspects: optimizing the base station’s beamforming vector and adjusting the phase shifts of the Reconfigurable Intelligent Surface (RIS). These optimizations aim to maximize the secure transmission rate for CUs while also ensuring effective and secure communication for D2D users. To achieve this, the paper employs a parallel Convolutional Neural Network (CNN) with a multi-scale attention mechanism. This advanced CNN model facilitates efficient resource allocation, thereby improving the overall security and performance of the communication system.

Here are three key contributions for the paper:

Introduction of a CNN-Based Resource Allocation Model: The paper introduces a novel resource allocation scheme based on parallel CNN. This model effectively optimizes base station beamforming vectors and RIS phase shifts to maximize the secure transmission rate for CUs while maintaining normal and secure communication for D2D users. The integration of CNNs provides a sophisticated approach to addressing challenges in spectrum utilization and network flexibility, enhancing the efficiency and security of embedded system communications.

Optimization of Interference Management and Secrecy Rate: The proposed scheme tackles the issue of interference caused by D2D users reusing CU spectrum resources. By optimizing RIS phase shifts and beamforming vectors, the model effectively suppresses interference and improves system secrecy rates. This contribution is significant for enhancing the overall security and performance of communication systems, particularly in scenarios with high user density and spectrum reuse.

Development of a Multi-Scale Residual Module in CNN Layers: The paper innovatively incorporates multi-scale residual modules into the convolutional layers of the CNN model. This enhancement allows for more accurate and effective resource allocation by considering various scales of data, which improves the model’s ability to handle complex communication scenarios. Simulation results demonstrate that this approach significantly boosts the secrecy rate and ensures secure multimedia communications, outperforming traditional methods.

Related research work

Ensuring communication quality and security is crucial in embedded system communications. In multimedia computing environments, enhanced communication quality facilitates faster information exchange between embedded systems and improves the overall user experience. Concurrently, ensuring communication security is vital to protecting user privacy and preventing information leakage, which could otherwise result in significant data loss.

D2D technology enables spectrum resource sharing between D2D users and the CU. However, this technology can also introduce additional system interference, which may adversely affect communication quality and potentially disrupt normal operations. To mitigate such interference, various resource allocation algorithms have been proposed. For instance, Literature11 addresses the energy efficiency optimization of cell D2D systems by transforming the resource allocation problem into an equivalent subtraction-based problem. Literature12 introduces two novel resource allocation schemes to tackle orthogonality loss issues in the fusion communication between CU and D2D users, thereby enhancing throughput and reducing associated costs. Literature13 analyzes the average energy efficiency of multi-D2D communication within a Rayleigh fading channel and theoretically derives the optimal transmission power for the CU. Additionally, Literature14 explores D2D communication by optimizing the transmission power of D2D users and deriving the conditions under which users opt for D2D communication modes. Literature15 critiques the challenge of solving mixed-integer nonlinear programming optimization problems in long-term evolution networks and proposes a greedy heuristic algorithm to address D2D resource allocation issues, thus reducing interference to the cellular network and improving system performance.

In D2D communication, devices with embedded16 systems can communicate at higher rates over short distances, which can alleviate some of the base station’s load. Nonetheless, ensuring the availability and security of communication remains essential for scaling D2D applications effectively. It is imperative to uphold the legitimacy, data confidentiality, integrity, and authentication of users on both ends of the communication to achieve reliable and secure D2D interactions. This prevents security risks such as data eavesdropping, tampering, discarding, and privacy infringement. Literature17 proposes a key agreement scheme between devices that leverages the unique properties of wireless channels to establish a universal encryption key. This protocol is designed to resist eavesdropping and spoofing attacks, thus enhancing communication security.

RIS-assisted D2D communication resource allocation system based on multi-scale parallel CNN

This paper mainly realizes D2D communication resource allocation technology applied in an embedded system under the background of the multimedia computer. If RIS is deployed in a D2D communication system, the controller is responsible for information interaction with a base station and intelligently controls the phase shift of transmitting elements. By optimizing the beamforming vector and RIS phase shift of the base station, the system security level is improved. The multi-scale parallel CNN model is added to the D2D channel model, and the convolution layer is used to extract the channel state information.

RIS auxiliary D2D communication system

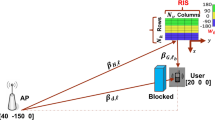
A downlink of RIS-assisted D2D communication system is established. As shown in Fig. 1, the base station is equipped with M antennas, and a CU and K pairs of D2D users are distributed around the base station. Each pair of D2D users includes a D2D transmitter (DT) and a D2D receiver (DR). Considering the actual cost and feasibility, the reflection phase of RIS is taken as a discrete value, in which RIS contains n reflection units. It is assumed that the phase shift of each reflection unit is 2 bit, and the phase shift range is [0, 2π]. In particular, assuming that the channel information state is known, the channel gains from BS to RIS, Cu, Dr, and Eve are respectively \(HBI \in {{\mathbb{C}}^{N \times M}},h_{{BC}}^{H} \in {{\mathbb{C}}^{1 \times M}},g_{{BD}}^{H} \in {{\mathbb{C}}^{1 \times M}},g_{{BE}}^{{}} \in {{\mathbb{C}}^{1 \times M}}\);The channel gains from RIS to Cu, Dr and Eve are\(h_{{IC}}^{H} \in {{\mathbb{C}}^{1 \times N}},h_{{ID}}^{H} \in {{\mathbb{C}}^{1 \times N}},g_{{IE}}^{H} \in {{\mathbb{C}}^{1 \times N}}\);The channel gains from DT to RIS, Dr, Cu and Eve are\(h_{{DI}}^{{}} \in {{\mathbb{C}}^{N \times 1}},h_{{DTDR}}^{{}} \in {{\mathbb{C}}^{1 \times 1}},g_{{DC}}^{{}} \in {{\mathbb{C}}^{1 \times 1}},g_{{DE}}^{H} \in {{\mathbb{C}}^{1 \times 1}}\).

Fig. 1
figure 1

RIS-assisted D2D communication system.

Full size image

mm-wave D2D channel model

In this paper, Saleh valenzula theoretical channel model18 is adopted, the channel vector is expressed as:

$$hk,m=\sqrt {\frac{N}{{Lk,m}}} \sum\limits_{{l=0}}^{{Lk,m}} {\alpha _{{k,m}}^{{(l)}}} a(\varphi _{{k,m}}^{{(l)}},\theta _{{k,m}}^{{(l)}})$$
(1)

Among them,\(Lk,m\)represents the number of multipaths between the m-th sub reflector and the k-th user;\(\alpha _{{k,m}}^{{(l)}}\)represents the gain of the 1st path;\(\varphi _{{k,m}}^{{(l)}}\)and\(\theta _{{k,m}}^{{(l)}}\)Indicates the azimuth and elevation of the i-th path;\(a(\varphi _{{k,m}}^{{(l)}},\theta _{{k,m}}^{{(l)}})\)is the array response vector, which can be expressed as:

$$a(\varphi ,\theta )=aaz\left( \varphi \right) \otimes ael\left( \theta \right)$$
(2)

Where, the horizontal and vertical array response vectors are respectively:

$$aaz\left( \varphi \right)=\frac{1}{{\sqrt {Ns1} }}{\left[ {{e^{\frac{{j2\pi d1\sin \varphi }}{\lambda }}}} \right]^T},i \in I(Ns1)$$
(3)
$$ael\left( \theta \right)=\frac{1}{{\sqrt {Ns2} }}{\left[ {{e^{\frac{{j2\pi d2\sin \theta }}{\lambda }}}} \right]^T},j \in I(Ns2)$$
(4)

Among them,\(\lambda\)is the signal wavelength,\(d1\)and\(d2\)are the horizontal and vertical spacing of elements,\(Ns1\)and\(Ns2\)represent Antenna elements in horizontal and vertical directions respectively.

RIS Technology

As a new revolutionary technology, reconfigurable intelligent surface (RIS) can realize the high efficiency of spectrum and energy6. Specifically, RIS is an electromagnetic artificial surface composed of many reflection units, where the phase and amplitude of the incident signal can be adjusted by software programming to improve the signal quality at the receiving end without additional energy consumption. Therefore, RIS can be used to design passive beams, that is, by changing the reflection coefficient of each reflection unit to enhance the required signal and suppress interference. The typical operating architecture of RIS is shown in Fig. 2, which usually consists of an antenna array integrated with many reflectors and a controller. The controller connected with RIS can adjust the reflection coefficient intelligently and communicate with other network components to realize the reconfiguration of wireless communication environment, to improve the anti-interference ability of D2D communication system at the physical layer level.

Fig. 2
figure 2

Typical working architecture of RIS.

Full size image

Multi-scale parallel CNN

To solve the problems of difficult optimization, slow transmission speed and poor security performance in D2D communication system, a multi-scale parallel CNN model is proposed in this paper, as shown in Fig. 3. Firstly, the convolution layer is used to extract the channel state information; Then, the best resource allocation scheme is selected through the full connection layer. The parallel CNN model can not only reduce the complexity of a single model, but also enhance the stability and scalability, which can upgrade the security level of the system while significantly reducing the complexity and running time.

Fig. 3
figure 3

Parallel CNN model.

Full size image

Firstly, a parallel computing model composed of two CNN is constructed, and the specific parameters of each CNN model are set; Then, the outliers far away from the cluster are regarded as outliers and eliminated, and the remaining data samples are normalized to get the required data set, and the data set is divided into a training set and verification set in the ratio of 8:2. Finally, the training set is used to train the model, and the verification set is used to verify the effect of the parallel CNN model.

Model structure

In the multi-scale parallel CNN architecture depicted in Fig. 4, eachCNN is designed with a structured approach to function optimization. The architecture integrates ReLU activation functions and incorporates a multi-scale residual module to enhance both feature extraction and learning capabilities. The ReLU activation function is applied across various stages, including convolutional and pooling layers, to introduce non-linearity. This function outputs the input directly if it is positive; otherwise, it outputs zero. By doing so, ReLU facilitates the network’s ability to learn complex patterns and maintain sparsity in activations, which contributes to computational efficiency and improved convergence rates.

The architecture includes two fully connected layers that play a crucial role in aggregating features and transitioning to a more compact representation. The first fully connected layer consists of 256 neurons, each activated by the ReLU function. This layer serves to condense the high-dimensional feature maps into a flattened representation that is suitable for further processing. The subsequent fully connected layer contains 64 neurons, also utilizing ReLU activation, and further refines the features extracted by the previous layer. This dense layer offers a more compact representation of the learned features, preparing them for the final output stage.

In terms of loss functions, the Mean Squared Error (MSE) is employed in the output layer of the CNN to measure the average squared difference between the predicted values and the actual values. This loss function is particularly suitable for regression tasks where the goal is to minimize the error between the predicted and true continuous values.

Additionally, the Softmax function, although not a loss function per se, is integral to classification tasks within the CNN framework. Softmax converts the output scores (logits) of the final layer into probabilities by exponentiating the logits and normalizing them across all possible classes.

While MSE is conventionally used for regression tasks, classification tasks typically utilize cross-entropy loss in conjunction with the Softmax function. The use of MSE with Softmax might be unconventional unless the network architecture addresses both regression and classification tasks separately. In such cases, different branches of the network may handle regression and classification outputs independently, each utilizing the most appropriate loss function for its specific task.

Fig. 4
figure 4

Structure of a single CNN.

Full size image

A CNN model is used to solve the beamforming vector f, which is constructed as a regression problem. Another CNN model solves the phase shift θ of N reflection units in RIS, which is a classification problem. Specifically, each model consists of the following two parts.

  1. (1)

    The feature extraction part, which consists of three convolution layers, is responsible for extracting key features from the channel information state.

  2. (2)

    The resource selection part, which is composed of two fully connected layers, uses the extracted features to select the best resource allocation scheme. Because each CNN in the parallel CNN model can be trained and used independently, the running time will be significantly reduced.

The multi-scale residual module is an advanced architectural component in CNN designed to enhance feature extraction across different scales. This module incorporates residual connections and multi-scale processing, which significantly improves the network’s ability to capture and represent both local and global patterns within the data. Residual connections, which bypass one or more convolutional layers, help address the vanishing gradient problem and enable more effective training of deeper networks. By facilitating the direct passage of input to the output of the block, these connections mitigate degradation issues and ensure smoother gradient flow during backpropagation. Additionally, the multi-scale processing aspect of the module allows the network to learn features from various granularities, aggregating information from multiple convolutional layers. This capability enriches the feature representation, making the network more adept at understanding complex patterns.

The integration of bottleneck residual modules with multi-scale residual modules amplifies the CNN’s capacity for feature extraction. Bottleneck residual modules facilitate the construction of deeper networks with fewer parameters, balancing efficiency and performance. This design approach enables the network to capture complex patterns while reducing computational costs. Combining these modules with standard convolution residual modules enhances the network’s width, allowing for the processing of a broader range of features. This combination not only increases the network’s ability to learn from extensive feature sets but also contributes to improved model performance. Through these enhancements, the multi-scale residual module, in conjunction with bottleneck and convolution residual modules, plays a crucial role in advancing CNN architectures.

In this paper, the multi-scale residual modules added in the first and third convolution layers mainly absorb the multi-scale connection idea of ResNet network, and by combining the bottleneck residual module with the convolution residual module, the width of CNN is enlarged to help the model extract more multi-scale feature information.

AdamW algorithm optimization

After research, it is found that the convergence of the model cannot be effectively guaranteed during training, and there are some problems such as non-convergence or slow convergence. To better deal with the convergence problem of the model, AdamW algorithm19 adds weight attenuation factor when updating parameters w. Generally, other training parameters and methods of 0.01 are the same as Adam’s algorithm. Compared with Adam’s algorithm, AdamW algorithm often has less loss in training set and test set, and also produces better generalization performance when the same training times are carried out.

The AdamW optimization algorithm is an extension of the Adam algorithm, designed to enhance regularization and generalization by integrating weight decay directly into the parameter update rule. The choice of hyper-parameters plays a critical role in achieving effective training and model performance. In this study, a learning rate of 1 × 10−4 was selected, balancing the need for convergence speed with the risk of overshooting minima. This value is a common default for AdamW and typically requires empirical tuning based on specific datasets and models. 1, set to 0.9, controls the exponential decay rate for the first moment estimates, which represent the moving average of gradients. This value ensures a balance between incorporating past gradient information and adapting to current gradients, thus stabilizing training. Similarly, \(\beta\)2 was chosen as 0.999, which governs the exponential decay rate for the second moment estimates, reflecting the moving average of squared gradients. This setting provides adequate smoothing and stability in gradient variance estimation.

Weight decay \(\lambda\) is another crucial hyper-parameter in AdamW, set to 0.01 in this study. Weight decay functions as a regularization technique that penalizes large weights, thereby mitigating overfitting. This choice, though adjustable, is a typical starting point that aligns with the regularization needs of many models. The epsilon \(\varepsilon\) parameter, set to 1 × 10−8, ensures numerical stability by preventing division by zero during the parameter update process.

The batch size, set to 32, determines the number of training examples used in each iteration. This value was chosen to strike a balance between computational efficiency and memory constraints. Larger batch sizes could accelerate training but would demand more memory, while smaller sizes might improve generalization. Additionally, the number of epochs, set at 50, represents the total number of passes through the entire dataset. This number provides a reasonable starting point for model training, though it should be monitored and adjusted based on convergence behavior and validation performance.

The training process involves initializing the model parameters and the AdamW optimizer with the specified hyper-parameters. During each training iteration, the forward pass computes the model’s predictions and the loss, followed by a backward pass to calculate gradients. The AdamW update rule then applies the parameter updates, incorporating the weight decay term. Post-iteration, the model’s performance is evaluated on a validation set to monitor for overfitting and convergence.

Training process

Each element of millimeter-wave channel matrix has amplitude and phase, which is transformed according to Euler formula, and each element is expressed as a complex number20. If training with parallel CNN model, it will be difficult to extract features by using complex numbers as input. Therefore, in this paper, the real and imaginary parts of elements are split and spliced into a two-dimensional matrix. According to the system configuration, the input data dimensions of the parallel CNN model are \(\left\{ {M+N+MN+{K^2}+{K^2}N,2} \right\}\).

In the training stage, firstly, the network parameters are initialized, the channel information is input into the neural network, and the output is calculated through the network forward propagation. Then, the output result is calculated to get the loss function, the network settings are then updated via back propagation. Finally, the output of the loss function is minimized and tends to be stable, and the training of the CNN model is completed.

In the testing phase, the trained model is evaluated by using the test data set. Firstly, the channel matrix is used as input to train the output parallel CNN model, and then the output results are compared to the traditional algorithm to calculate the prediction accuracy of the parallel CNN model. The specific process is as follows.

  1. (1)

    Construct a parallel CNN model and divide the data set into training set and testing set.

  2. (2)

    Weight the neurons in the initial model randomly, and set the learning rate, each batch of input data and training times.

  3. (3)

    Train the parallel CNN, input the training data, get the output value through forward propagation, calculate the error-by-error function, and use Adam optimizer to optimize the parameters in the network.

  4. (4)

    Repeat step (3) until the error value is less than the error tolerance or reaches the maximum training times.

  5. (5)

    Evaluate the performance of parallel CNN model by using verification set.

Experiment and analysis

Parameter setting

The effectiveness of the proposed algorithm is verified by simulation experiments. 2000 channel data are collected from the communication base station to train the model. The simulation platform is developed by Python 3. The system deployment is shown in Fig. 5.

The following three schemes are used for comparison: (i) The system does not deploy RIS (no RIS scheme); (ii) RIS is deployed in the system with random phase shift; and (iii) RIS is deployed in the system, and the phase shift of RIS is calculated by block coordinate descent method.

Fig. 5
figure 5

System deployment.

Full size image

The channel data and model parameter Settings are shown in Table 1.

Table 1 Parameter setting.
Full size table

Validation of multi-scale parallel CNN scheme

The variation of the accuracy and recall rate of the proposed model is shown in Fig. 6.

Fig. 6
figure 6

Accuracy and recall graphs.

Full size image

It can be seen from Fig. 7 that the accuracy and recall rate decrease with the increase in iteration times. If the iterations are 60, the training error tends to be stable and converges. This is mainly because the parallel multi-scale CNN proposed in this paper can extract more high-quality data.

The relationship between the maximum secret transmission rate of CU and the number of RIS reflection elements N is shown in Fig. 7.

Fig. 7
figure 7

Relationship between the maximum confidential transmission rate of CU and the number of RIS reflection elements N.

Full size image

Figure 7 provides a comprehensive illustration of the performance of the proposed multi-scale parallel CNN scheme in comparison to other schemes, specifically when the parameter.

PB is set to 25 dB and K is set to 15. The figure highlights a notable trend: as the number of RIS reflection elements increases, the maximum secrecy rate of the proposed scheme consistently improves. This trend underscores the scheme’s ability to effectively harness additional RIS reflection elements to enhance the security and efficiency of communication. At 30 reflection elements, the proposed scheme achieves a maximum secrecy rate that surpasses both the random phase-shifting scheme and the RIS-free scheme by 1.790 bits per second (bit/s) and 6.747 bit/s, respectively. This substantial improvement underscores the efficacy of the proposed scheme in enhancing secrecy rates.

The multi-scale parallel CNN scheme exhibits several significant advantages over traditional approaches. One of the primary benefits is its enhanced feature extraction capability. By employing multiple convolutional neural networks operating at different scales, the proposed scheme is adept at capturing a comprehensive range of features from the data. This multi-scale processing allows for the detection of both local and global features, thereby improving the accuracy and robustness of secrecy rate predictions.

In addition, the proposed scheme demonstrates superior performance in high noise conditions. The multi-scale parallel CNN approach enhances resilience to noise and interference, which is crucial for maintaining high secrecy rates under challenging conditions, such as those characterized by PB = 25 dB. This increased robustness ensures that the scheme remains effective even in less ideal scenarios.

Another notable advantage of the proposed scheme is its optimized resource utilization. The scheme achieves higher secrecy rates with a fewer number of RIS reflection elements compared to other methods. This efficiency not only translates into cost savings but also contributes to better resource management, making the scheme a practical and economical choice for real-world applications. Furthermore, the multi-scale parallel CNN scheme offers exceptional flexibility and adaptability. Its ability to process data at various scales allows it to adapt to dynamic environmental conditions and system parameters, ensuring consistent high performance across different scenarios. This adaptability is particularly valuable in environments where system parameters may fluctuate.

Finally, the significant improvement in secrecy rates achieved by the proposed scheme highlights its advanced security capabilities. The scheme’s superior performance in delivering higher secrecy rates compared to the random phase-shifting and RIS-free schemes demonstrates its effectiveness in securing communication channels.

The relationship between the maximum secrecy rate of CU and the transmission power PB of the base station is shown in Fig. 8.

Fig. 8
figure 8

Relationship between CU maximum secrecy rate and base station transmit power PB.

Full size image

If K = 15 and N = 40, the maximum secrecy rate of CU increases with the increase of Pb, and the proposed scheme is better than other benchmark schemes. The comparison shows that the security rate of RIS assisted system is obviously better than that of non RIS scheme, especially with the increase of transmitting power, the difference between RIS scheme and non RIS scheme is more obvious, because the RIS provides a new degree of freedom and diversity gain for the system.

The relationship between the maximum secrecy rate of CU and the number of D2D users K is shown in Fig. 9.

Fig. 9
figure 9

Relationship between CU maximum secrecy rate and the number of D2D users K.

Full size image

As can be seen from Fig. 9, if the base station transmit power Pb = 25 dB and RIS reflection element n = 40, with the increase of the number of D2D users, the maximum security rate of CU gradually decreases. The reason is that with the increase of D2D number, the interference of D2D users to Cu users will become more serious, but the maximum-security rate of Cu in the proposed scheme is still better than that of other benchmark schemes.

Since the other solutions do not consider the optimization of RIS phase shift and the system performance is poor, this paper mainly compares the operation time of the proposed parallel CNN model and block coordinate descent method under different RIS reflection elements and D2D numbers. The base station transmit power is PB = 25 dB. Only one variable of RIS reflection elements or D2D users is adjusted each time. The relationship between operation time and the number of RIS reflection elements and D2D users is obtained, as shown in Figs. 10 and 11.

Fig. 10
figure 10

Operation time and number of RIS reflection elements.

Full size image
Fig. 11
figure 11

Operation time versus the number of D2D users.

Full size image

Figure 10 provides a detailed comparison of operation times between the parallel CNN model and the block coordinate descent method, highlighting a clear performance advantage of the former. The data reveals that the operation time required by the parallel CNN model is significantly lower than that of the block coordinate descent method. This disparity becomes even more pronounced as the number of RIS (Reconfigurable Intelligent Surface) reflection elements increases. The efficiency of the parallel CNN model in handling larger numbers of reflection elements underscores its scalability and effectiveness in computational performance.

Furthermore, Fig. 11 illustrates the impact of the number of D2D users on operation times for both methods. As the number of D2D users increases, the operation time of the block coordinate descent method shows a marked increase, indicating that its computational complexity grows with additional users. In contrast, the running time of the parallel CNN model remains relatively stable and is consistently lower than that of the block coordinate descent method, regardless of the number of D2D users. This stability highlights the parallel CNN model’s robustness and efficiency in managing computational demands across varying user loads.

Model comparison

In the context of secrecy rate performance, our comparison reveals significant differences among various resource allocation methods, as shown in Table 2. The Max-Min Fairness Resource Allocation method, a traditional approach, achieves a secrecy rate of 3.5 bps/Hz, reflecting its focus on resource fairness rather than explicit secrecy optimization. The Water-Filling Algorithm, while improving spectral efficiency, offers a slightly better secrecy rate of 4.0 bps/Hz but does not specifically target secrecy enhancement. The Deep Convolutional Neural Network (DCNN)-based Resource Allocation model provides a noteworthy improvement, achieving a secrecy rate of 4.8 bps/Hz, thanks to its ability to learn complex patterns and optimize resource allocation. In comparison, the Recurrent Neural Network (RNN)-based Dynamic Allocation method yields a secrecy rate of 4.6 bps/Hz, which is slightly lower than the DCNN model, indicating that while RNNs handle temporal dynamics well, they may not optimize spatial resource allocation as effectively as CNNs. The proposed Parallel CNN Scheme demonstrates superior performance with a secrecy rate of 5.2 bps/Hz, underscoring its advanced capabilities in optimizing both base station beamforming and Reconfigurable Intelligent Surface (RIS) phase shifts. This result highlights the effectiveness of the proposed approach in addressing the challenges of secure multimedia communication.

Table 2 Comparison of secrecy rate and operation time of different models.
Full size table

In terms of operation time, the proposed Parallel CNN Scheme demonstrates exceptional efficiency. The operation time for the proposed scheme is 1.9 s, the shortest among the methods evaluated, reflecting its ability to deliver high performance with minimal computational overhead. The Max-Min Fairness Resource Allocation method has a moderate operation time of 2.5 s, consistent with traditional methods. The Water-Filling Algorithm, while having the shortest operation time of 2.0 s, sacrifices the improvement in secrecy rate for speed. On the other hand, the DCNN-based Resource Allocation model, due to its complexity, requires an operation time of 3.8 s. Similarly, the RNN-based Dynamic Allocation method takes the longest time at 4.2 s, attributable to the additional complexity in handling time-series data. The proposed Parallel CNN Scheme’s optimal balance of low operation time and high secrecy rate demonstrates its dual advantage in achieving efficient and secure resource allocation, making it a superior choice for practical applications requiring both performance and efficiency.

Conclusion

The fast advancement of multimedia computer communication technologies has resulted in that the technology of embedded system information sharing has gradually become the focus of research. To meet the security requirements of intelligent signal processing and physical layer in the communication process of embedded system, a RIS assisted D2D communication resource allocation scheme based on multi-scale parallel CNN is proposed to solve the problem of low spectrum utilization and poor network flexibility in the process of multimedia computer communication. The downlink of RIS assisted D2D communication system is established, and the RIS phase shift and beamforming vectors are optimized to suppress interference and improve the security rate of the system.

The proposed multi-scale parallel CNN for multimedia communication security in embedded systems holds significant real-world implications. In industries such as IoT and mobile devices, where security and efficient communication are paramount, integrating this solution could enhance the reliability and robustness of data transmission. By improving spectrum utilization and network flexibility, the proposed scheme can contribute to more secure and efficient communication systems. In practical terms, integrating this technology into existing systems may involve several challenges. Adapting legacy systems to support RIS-assisted D2D communication could require substantial modifications or upgrades. Additionally, ensuring compatibility with diverse communication standards and protocols will be essential for seamless integration. The impact on industries could be profound; for example, in IoT applications, enhanced communication security can lead to more secure smart devices and networks, reducing vulnerability to cyber threats. Similarly, in mobile devices, improved resource allocation and security can enhance user experience and extend battery life by optimizing communication efficiency. Addressing these challenges will be crucial for the successful implementation of the proposed solution. Future research should focus on developing practical deployment strategies, including system integration frameworks, compatibility solutions, and user-centric adaptations to ensure that the benefits of the multi-scale parallel CNN are realized in real-world applications.

Despite the advancements achieved, several limitations are evident in the current study. Firstly, scalability remains a critical challenge. The proposed multi-scale parallel CNN may face difficulties when applied to larger networks or environments with high-density devices, potentially leading to increased computational demands and inefficiencies. Future research should explore scalability solutions, such as hierarchical network structures or adaptive algorithms that can handle large-scale scenarios effectively. Secondly, real-time processing capabilities are a concern. The complexity of the multi-scale parallel CNN may impact the system’s ability to process data in real time, which is crucial for dynamic communication environments. Research into optimizing the CNN’s architecture or integrating hardware accelerators could enhance real-time processing performance. Additionally, the study’s focus on optimizing the RIS phase shift and beamforming vectors may not fully address resource allocation in highly constrained environments. Future work could investigate more robust optimization techniques or hybrid approaches combining different methodologies to improve resource allocation efficiency in such scenarios.