Introduction

Coronary artery disease, a leading cause of death worldwide, is closely associated with changes in vessel physiology such as atherosclerotic plaques narrowing the coronary arteries, with subsequent restriction of the coronary blood supply. Local blood flow dynamics, particularly Endothelial Shear Stress (ESS), have been shown to regulate signalling pathways driving such morphological changes, e.g. endothelial cell growth leading to neointimal thickening1,2. The anatomy of coronary arteries, represented by parameters such as vessel calibre, angulation, and curvature, directly influences the blood flow and, thus, the distribution and magnitude of ESS. This forms the “anatomy of risk” hypothesis, whereby the blood flow-induced shear forces, called haemodynamics, affect disease mechanisms - thus being directly associated with vessel shape characteristics. Bifurcating coronary segments are more likely to be affected by disease3, which can be attributed to their complex blood flow dynamics with both adversely high and low shear regions due to recirculation, stagnating, and rapid blood flow regions initiated due to the flow split from the main vessel into the smaller arterial segments3. Understanding these mechanisms may prove vital for risk stratification and ultimately preventative measures, especially in the Left Main (LM), which supplies the majority of cardiac tissue4.

Thus, vascular anatomy has repeatedly been suggested as a surrogate for adverse haemodynamics computations in individuals5,6, since these could be identified in medical images directly. However, until recently, limited spatial resolution and a 2D rather than 3D standard imaging have hindered the effective capture of complex coronary anatomical characteristics. This is particularly apparent compared to related, more advanced fields such as carotid research, since carotid arteries are comparatively easier to image as they are larger, stagnant, and close to the body surface7,8. Consequently, the detection of shape biomarkers for the carotid arteries is further developed and was demonstrated to directly correlate to shape features such as the angle of origin9, and vessel curvature10, showcasing the distinct relationship between vessel anatomy and adverse flow11. In fact, carotid anatomical characteristics have been used as actual age marker12, and disease risk factor13,14, which has been not accomplished for the coronaries to date but demonstrates the potential of such research efforts.

For the coronaries, anatomical characteristics have interdependent effects15,16, however, studies to date are limited to the consideration of a maximum of three or fewer anatomical parameters at once17. The adverse effect of tortuosity was reported in vivo repeatedly18,19, yet could not be confirmed with computational efforts20—likely due to the lack of consistent 3D measurement methods and mathematical definition21, as well as a lack of the consideration of personalised geometries22,23. Vessel diameter has not been extensively considered before, although its critical haemodynamics effect in combination with other shape characteristics has been demonstrated24,25. Moreover, the small number of patient-specific geometries tested (n\(\,<\,\) 25) is another gap in the literature to date16,17,26, especially considering the large anatomical variation found within a large population27. No other large-scale, patient-specific effort has attempted to link all prominent coronary arterial shape characteristics and adverse haemodynamics before this work as presented here.

Therefore, our aim is to unravel the relationship between coronary anatomy and adverse haemodynamics in a large-scale, patient-specific population (n = 127) using all potential anatomical bifurcation factors identified (n = 11) to explore the feasibility of using coronary shape characteristics as biomarkers of adverse blood flow in the LM.

Methods

We collected 127 CTCA images of patients (males 42 / 33%, females 85/ 67%, age median 57, age range 38-81, Table 1) with suspected coronary artery disease for virtual reconstruction of the LM coronary bifurcation and subsequent computational haemodynamics analysis using transient Computational Fluid Dynamics (CFD) modelling.

Patient inclusion and medical imaging protocol

This study was approved by the local institutional ethics committees of the University of Auckland (Ref. 022961) and the University of New South Wales (Ref. HC190145), with informed and written consent received from all participants. This research was performed in accordance with the relevant guidelines and regulations and in accordance with the Declaration of Helsinki. A retrospective review of patients referred to Intra Care (Auckland, NZ) was conducted to include those with no stenosis or calcification within the entire epicardial coronary arteries. We further excluded patients if they had intermediate arteries or had CTCA images of insufficient quality for segmentation or 3D vascular reconstruction due to respiratory or motion artefacts. CTCA images were obtained using a multi-detector CT scanner (GE Lightspeed 64 multi-slice scanner, USA) following a retrospective ECG gating protocol. The contrast-enhanced images were obtained through intravenous administration of a non-ionic medium (Omnipaque 350, GE Healthcare). Where necessary, a beta blocker was used to achieve a resting heart rate of 60 beats per minute to reduce motion artefact.

Table 1 Patient demographics, coronary anatomical and haemodynamics characteristics.
Full size table

Coronary segmentation and reconstruction

The image sets were semi-automatically segmented as previously described28. Briefly, an experienced analyst used standard software (Osirix CMIV CTA version 4.1.2 32-bit and MiaLight version 1.0) for segmentation, generating the surface mesh and vessel centrelines semi-automatically taking approximately 20 minutes per case. The resulting geometries were then imported into the open-source Vascular Modelling Tool Kit (VMTK)29 for automatic smoothing (Taubin30 filter with a passband of 0.03 cut-off and 30 iterations), and adding of flow extensions (4x radius perpendicular to the median direction of the last 5mm) before meshing using patch-conforming, unstructured tetrahedral elements with five boundary layers.

Quantification of coronary geometric indices

The LM bifurcation section within 10 mm of the bifurcation point was extracted and the shape characteristics were automatically quantified using an in-house software15 according to the European Bifurcation Club’s naming convention31: (i) Angle A: the angle between LM and LAD, (ii) Angle B: the angle between LAD and LCx, (iii) Inflow Angle: the angle between LM and the plane formed by the LAD and LCx as a measure of how acute or obtuse the LM branches from the aortic arch, (iv) tortuosity of each vessel: The curvature was calculated at each centreline point, quantifying the deviation from a straight line. The tortuosity was defined as the mean curvature, which was found to be superior to the tortuosity index based on prior work21, (v) median diameter for each vessel, and (vi) Finet’s ratio, defined as \(\frac{\text {LM diameter}}{\text {LAD diameter} + \text {LCx diameter}}\). Figure 1 summarises the relevant geometric features.

Fig. 1
figure 1

Schematic of coronary anatomical metrics, including angles A, B, and C, inflow angle, Left main (LM), Left circumflex (LCx), Left anterior descending (LAD) and the bifurcation point. Example values are shown for one case.

Full size image

Computational fluid dynamics

The vascular walls were modelled as rigid bodies since a previous computational study showed little haemodynamics difference between rigid-wall and compliant fluid-structure interaction simulations in cycle averaged metrics32. A tetrahedral grid with five prism layers was generated for the blood flow domain. After a sensitivity analysis, the mesh cardinality was approximately \(\hbox {2x10}^6\) with a time-step of 0.002 seconds. The Navier-Stokes equations governing the laminar fluid flow were resolved using CFX (version 19.3, ANSYS, USA). Flow profile in coronary arteries is blunted due to the pulsatile nature of the flow33, hence, a uniform (plug) velocity profile was prescribed at the inlet, although prior literature suggests the flow profile does not have a significant impact with flow extensions included34. We calculated the average volumetric inflow rate for each patient based on the LM diameter35. We utilized a generic inflow rate vs time waveform adapted from36, which was scaled to have the appropriate average inflow rate. A zero reference static pressure condition was defined at both outlets in line with experimental observations7, and deemed suitable for non-diseased cases. Four consecutive cardiac cycles were simulated, with the results taken from the fourth cycle to minimise the transient start-up effects. A residual convergence criterion of \(\hbox {10}^{-4}\) was used. A standard non-slip boundary condition at the vessel walls and shear-thinning Carreau-Yasuda model were applied37. Computations were performed on the UNSW Katana cluster, taking approximately 25 CPU-hours per bifurcation.

Quantification of adverse haemodynamics

We analysed TAESS, OSI, RRT, and TSVI. LowTAESS38 quantifies exposure to adversely low shear stress, highOSI39 areas with changes in the direction of ESS throughout the cardiac cycle, and highRRT39 attempts to combine both metrics, thereby capturing both low and oscillating shear stress. TSVI40 quantifies the variability of ESS expansion and contraction. These are calculated as follows:

$$\begin{aligned} \text {TAESS}&= \frac{1}{T} \int _0^T{|\mathbf {\tau }_w}|dt \end{aligned}$$
(1)
$$\begin{aligned} \text {OSI}&= \frac{1}{2} \left( 1- \frac{|\int _0^T{\mathbf {\tau }_w}dt|}{\int _0^T{|\mathbf {\tau }_w}|dt}\right) \end{aligned}$$
(2)
$$\begin{aligned} \text {RRT}&= \frac{1}{(1-2\cdot \text {OSI})\cdot \text {TAESS}} \end{aligned}$$
(3)
$$\begin{aligned} \text {TSVI}&= \sqrt{\frac{1}{T} \int _{0}^{T}\left[ \nabla \cdot \frac{\tau _w}{|\tau _w|}-\overline{\nabla \cdot \frac{\tau _w}{|\tau _w|}}\right] ^2} \end{aligned}$$
(4)

Where \(\mathbf {\tau }_w\) is the flow-induced shear stress vector at the arterial vessel wall, and T denotes the cardiac cycle period. We normalised and computed the percentage of LM arterial wall area exposed to adverse haemodynamics across all cases. Adverse thresholds as per literature include lowTAESS\(\,<\,\) 0.5Pa17,22, and highOSI > 0.122, which have both been associated with neointimal thickening and plaque formation. While the threshold for RRT can be calculated from the TAESS and OSI thresholds (resulting in  > 2.5 Pa−1 in this case), we chose to use a threshold of  > 4.17 Pa−1 as commonly used in literature17. We note that these thresholds are not universal. However, we investigated whether different choices of thresholds (lowTAESS\(\,<\,\) 0.4Pa, lowTAESS\(\,<\,\) 0.6Pa, highOSI > 0.2) affected the overall findings and found negligible differences (see Supplementary Table 4 and 5 in the supplementary material). Use of absolute thresholds has been found to be appropriate for population level considerations41, however recent literature indicates alternative thresholding methods perform better for individual patient-based prediction41. TSVI was averaged over the luminal surface42. Recent literature has also suggested measures of helical intensity43 and ESS multi-directionality44,45 as promising disease risk metrics. Other haemodynamics parameters such as ESS Gradient (ESSG), or instantaneous ESS have also been used in the past, yet their impact is more ambiguous46. Moreover, the implications of instantaneous haemodynamics throughout the cardiac cycle have never been established.

Statistical analyses

Statistical analyses were performed using the python statsmodels47 package. Continuous and categorical variables were expressed as mean and Standard Deviation (SD), and counts and percentages, respectively. Independent two-sided Welch’s t-tests were used to examine the differences in each anatomical or haemodynamics metric between sexes and between patients with and without hypertension or smoking history. This test is robust to violations of homoscedasticity (where the subgroups have unequal variance)48 and violations of normality assumption49. Analysis for diabetes was not conducted due to the limited sample size (n = 3).

Correlations between each of the shape metrics and the adverse haemodynamics were examined using standardised regression coefficients, i.e. the variables were standardised to have unit variance such that the regression coefficient measures how many standard deviations the output will change in response to a one-standard-deviation change in the predictor. The obtained p-values were adjusted using Holm-Bonferroni correction50 to prevent inflated false positive rates due to multiple comparisons. A p-value \(\,<\,\) 0.05 was considered statistically significant throughout this work.

To analyse the predictive performance of the studied metrics, a backward multiple regression procedure51 was used to find a set of predictors with the lowest Akaike Information Criterion (AIC)52. This balances prediction performance and model simplicity, avoiding overly complex models.

Results

Variations in coronary anatomy and haemodynamics

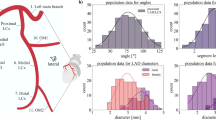
Coronary anatomy varied widely across the 127 patients (Table 1, partly previously reported elsewhere27, but we include curvature, exclude intermediate arteries and apply a Bonferroni correction here), with the inflow angle showing the largest variation from − 40 to \(\hbox {45}^{\circ }\) with a coefficient of variation of 88.7%. Other parameters also varied markedly, including the curvature of the LM (25.7%) and the LCx (23.7%). Notably, Finet’s ratio showed a very small variation of only 5.8% across all patients (Table 1).

After adjusting for multiple comparison testing, there were no statistically significant differences between patients with and without hypertension, and smokers and non-smokers. Females had significantly smaller diameters in all LM branches compared to males (mean difference, LM 0.69 mm, 95% CI 0.48 to 0.898, p\(\,<\,\) 0.001; LAD: 0.60 mm, 95% CI 0.41 to 0.79, p\(\,<\,\) 0.001; LCx: 0.63 mm, 95% CI 0.42 to 0.84, p\(\,<\,\) 0.001). The difference in vessel diameter persisted after adjusting for Body Mass Index and Body Surface Area. Females showed higher curvature in all vessels with a difference of LM: 0.062 mm−1 (95% CI 0.025 to 0.099, p\(\,<\,\) 0.001); LAD: 0.063 mm−1 (95% CI 0.031 to 0.096, p\(\,<\,\) 0.001); and LCx: 0.072 mm−1 (95% CI 0.034 to 0.84, p\(\,<\,\) 0.001). While the Inflow Angle seemed larger in females, this difference was not significant after adjusting for multiple comparison testing. The statistical results for hypertension, smoking and sex are included in the Supplementary Material (Supplementary Tables 1–3).

Strong variations were found for all haemodynamics metrics: lowTAESS@0.5 (25.62 ± 9.36 %), highOSI@0.1 (3.08 ± 2.36 %), highRRT@4.17 (4.84 ± 3.06 %), and meanTSVI (0.34±0.08). Subgroup analyses did not show statistically significant effect of hypertension or smoking history on adverse haemodynamics metrics. While there was no significant difference in lowTAESS between males and females, both highOSI@0.1 (4.6% vs. 2.35%, p\(\,<\,\) 0.001) and highRRT@4.17 (6.1% vs 4.2%, p=0.01) were higher in males, while meanTSVI was higher in females (0.302 vs 0.358, p\(\,<\,\) 0.001).

Correlations between anatomy and coronary haemodynamics

For lowTAESS only the Finet’s ratio correlation was statistically significant (\(\beta\) = -0.84, p \(\,<\,\) 0.001). For highOSI, both diameters (LM: \(\beta\) =0.69, p\(\,<\,\) 0.001; LAD: \(\beta\) =0.74, p\(\,<\,\) 0.001; and LCx: \(\beta\) =0.74, p\(\,<\,\) 0.001) and curvature (LM: \(\beta\) =-0.367, p\(\,<\,\) 0.001; LAD: \(\beta\) =-0.484, p\(\,<\,\) 0.001; and LCx: \(\beta\) =-0.519, p\(\,<\,\) 0.001) had a statistically significant effect. The Finet’s ratio was not statistically significantly correlated to highOSI after adjusting for multiple comparisons. For highRRT, diameters (LM: \(\beta\) =0.403, p\(\,<\,\) 0.001; LAD: \(\beta\) =0.542, p\(\,<\,\) 0.001; and LCx: \(\beta\) =0.525, p\(\,<\,\) 0.001), daughter branch curvatures (LAD: \(\beta\) =-0.269, p=0.018; and LCx: \(\beta\) =-0.368, p\(\,<\,\) 0.001), and the Finet’s ratio (\(\beta\) =-0.488, p \(\,<\,\) 0.001) showed a statistically significant correlation. Diameters (LM: \(\beta\) =-0.552, p\(\,<\,\) 0.001; LAD: \(\beta\) =-0.579, p\(\,<\,\) 0.001; and LCx: \(\beta\) =-0.513, p\(\,<\,\) 0.001), daughter branch curvatures (LAD: \(\beta\) =0.376, p\(\,<\,\) 0.001; and LCx: \(\beta\) =0.333, p=0.001) correlated with meanTSVI. Correlations are shown in Fig. 2 and Table 2.

Fig. 2
figure 2

Correlogram of the coronary anatomical metrics and the percentage of arterial wall area exposed to adversely low Time-Averaged Endothelial Shear Stress (lowTAESS\(\,<\,\)0.5Pa), high Oscillatory Shear Index (highOSI >0.1) and Relative Residence Time (highRRT > 4.17 Pa−1) with dark red (1) being highly positively correlated, dark blue (-1) being highly inversely correlated and grey (0) no correlation.

Full size image
Table 2 Independent tests of effects of patient weight, BMI and geometric features on adverse haemodynamics metrics with * indicating the significance of p\(\,<\,\)0.05.
Full size table

Multiple regression model

The diameters for LAD and LCx were pre− emptively removed from the set of predictors to avoid high multi-collinearity in the multiple regression model. At each iteration, one predictor was removed that would result in the set of predictors with the lowest AIC, until AIC could not be decreased by removing predictors. The final retained predictors for each haemodynamics metric are shown in Table 3, whereby the regression coefficient signifies the amount by which a change in the respective haemodynamics metric must be multiplied to give the corresponding average change in the retained feature, or the amount of which the retained feature changes for a unit increase in the haemodynamics metric. This means a larger value indicates a greater effect, with a positive/negative correlation according to the coefficient.

Our results indicate that a large percentage of the local haemodynamics can be explained with coronary shape characteristics, including 79% of the variance in lowTAESS, and 63% and 58% of the variance for highOSI and high RRT, respectively (Table 3). The prediction ability was lower for meanTSVI, only accounting for 36% of the variance.

Table 3 Multiple linear regression between coronary anatomy and haemodynamics.
Full size table

Discussion

We have retrospectively analysed 127 CTCA scans of patients with suspected coronary artery disease and unremarkable stenosis or calcification. This constitutes the largest patient cohort, whereby all coronary bifurcation shape characteristics were correlated to haemodynamics. In summary, our results show that a local haemodynamics can largely be explained with coronary shape characteristics: (i) a smaller Finet’s ratio (meaning the daughter branches are larger than common in comparison to the main vessel) significantly correlated to larger areas of adversely lowTAESS; (ii) larger branch diameters and stronger curvatures increased highOSI while at the same time decreasing meanTSVI; and (iii) small Finet’s ratio (daughter branches notably smaller than the main branch), large LAD and LCx diameter, and stronger curvatures each also increases highRRT. It should be noted that Finet’s ratio showed the lowest variation within the cohort, suggesting small changes in Finet’s ratio have a substantial impact on haemodynamics.

These metrics are strongly associated with the formation and progression of plaques as documented and evidenced by both in vitro53 and cellular pathophysiology54 studies.

Left main branch diameters and curvatures showed an interdependent, significant effect which appears sex-specific. It should be noted that tortuosity measured as tortuosity index has often been reported for this purpose in clinical literature. However, this needs to be interpreted with caution because it was demonstrated that this can lead to inconsistent results due to a variation in heart sphericity introducing inaccuracies due to three-dimensionality not being captured, with the mean average branch curvature as a superior measure21.

We found that curvature and vessel diameters affect TSVI in opposite direction of OSI and RRT, such that larger curvature and smaller diameters result in higher TSVI while decreasing OSI and RRT. Both highOSI and highRRT indicate stronger oscillatory shear stress (meaning topically periodically recurring), often associated with increased disease risk, while high TSVI is likewise associated with increased risk. As women tend to have smaller and more tortuous vessels, resulting in higher TSVI as measured in our data, this may suggest differences in disease development between male and female cases driven by the differences in TSVI. Sex-specific haemodynamics are further explored elsewhere55. This has not been described in the literature before, however, recent work hypothesised the interdependent significance of diameter with curvature in idealised work25.

No significant differences between the smoking versus non-smoking and hypertensive versus normal non-hypertensive subgroups were found after adjusting for multiple comparison testing. This potentially indicates that smoking and hypertension may not affect arterial remodelling in patients with coronary artery disease symptoms but without notable stenosis or calcification. Prior literature on this is inconsistent, however, with some work reporting smoking and hypertension correlated to increased tortuosity18, while others found no effect56. It is possible that the differences are too small to be detected at the statistical power in this study and future studies are warranted.

We note that the cases included in this study showed low oscillatory shear stress, resulting in small a percentage of the vessel being exposed to high OSI and RRT (the case-wise maximum was 12.1% for highOSI and 15.7% for highRRT). Therefore, the OSI and RRT results should be interpreted with caution. The relatively low values of OSI and RRT is in line with previous coronary studies44,57. The cohort included only symptomatic patients in the absence of significant stenosis and calcium. Whether our findings would apply to a population with stenosis onset could not be stratified from our results and warrants future studies. A wider demographic representation may also provide additional valuable insights since increasing reports in literature point towards important population cohort differences, including ethnicities58, and age59. This study relies on commonly used absolute threshold-based haemodynamics assessment criteria. We have demonstrated that specific thresholds of the metrics considered did not affect the result. Still, pathophysiological processes ruling coronary artery disease have been found to be a continuum rather than a specific cut-off60. Absolute thresholds as used here may not be appropriate for patient specific predictions41, and therefore improved consideration of these thresholds should be further considered in future studies. Similarly, we use a generic flow-rate versus time waveform for all patients, which can be improved by more sophisticated boundary conditions such Windkessel and lumped parameter models taking more patient-specific considerations into account61. Mechanical forces within the vasculature are not considered here but may have an important effect62. Additionally, while the assumptions of rigid vessel walls and no cardiac motion have been commonly used in coronary CFD modelling and found not to significantly affect cycle average haemodynamics32,63, the impacts on the morphological metrics are less clear. This study study focuses on the left main bifurcation geometrical features, which should not be significantly affected by cardiac motion. The specific translation of this work into clinical practice must be further determined via clinical trials to validate the predictive power within the computational assumptions and simplifications made here.

Overall, our work sheds light on using coronary anatomical features to link and predict adverse local haemodynamics in the coronary left main bifurcation without stenosis. The results are promising in that some coronary anatomy characteristics are found to directly affect key pathophysiological drivers. We show that well-established indicators for adverse endothelial pathophysiological processes (TAESS, OSI, RRT, and to some extent TSVI) can be predicted from geometrical features of the left main bifurcation, thereby allowing calculations of these risk metrics without computationally expensive CFD simulations. This may allow better patient-specific considerations of risk of coronary disease development in the future.