ExCS: accelerating code search with code expansion

Abstract

Efficiently searching and reusing code from expansive codebases is pivotal for enhancing developers’ productivity. In recent times, the emergence of deep learning-driven neural ranking models, characterized by their vast dimensions and intricate interaction mechanisms, has been noteworthy. Yet, these models, in real-world scenarios, pose computational challenges due to their high dimensionality. Moreover, models rooted in interaction necessitate querying every piece of code within a voluminous corpus. While these methodologies offer superior accuracy, their online retrieval process is considerably more time-consuming compared to traditional Information Retrieval (IR) techniques. Addressing this, we introduce “ExCS”, an innovative code search tool designed to expedite the code search process without compromising on accuracy. ExCS innovatively employs code expansion in its offline phase, leveraging predictions on potential queries for specific codes, thereby enriching the code’s semantic depth. During online retrieval, ExCS prioritizes IR-based methods to pinpoint a concise set of persuasive candidates. Our evaluations, conducted on the Java dataset from CodeSearchNet, reveal that ExCS achieves a remarkable 90% reduction in retrieval duration while maintaining an impressive 99% retrieval accuracy.

Introduction

Code search is a fundamental task in software development, facilitating troubleshooting, code reuse, and understanding. Estimates suggest developers allocate around 15% of their time to search-related tasks. This statistic accentuates the necessity for proficient code search tools, which could substantially boost development productivity and trim costs¹.

Navigating through vast codebases to locate desired code snippets is a challenging endeavor, primarily due to the semantic disparity between natural language queries and code^2,3,4. A variety of strategies have been probed to surmount this challenge, encompassing information retrieval (IR)-based methods and deep learning-based techniques. While the former boasts speed, they stumble when it comes to bridging the semantic chasm. On the flip side, deep learning methods shine in unraveling intricate query-code relationships, albeit at the cost of computational efficiency owing to the large dimensions of the models and complex mechanisms employed^{5,6,7,8,9,10,11,12,13}.

Historically, the bulk of research efforts have been channeled towards ameliorating retrieval accuracy, leaving a void in the domain of retrieval efficiency, particularly on extensive code bases. The crux of deep learning approaches for code search revolves around direct ranking of the entire corpus of source code snippets during the search process, which inevitably spirals into high computational expenses. Strategies utilizing separate representation vectors for code and description necessitate the computation of similarity between the target query vector and all code representation vectors in the corpus for each retrieval, setting a high bar for the dimension of representation vectors to achieve commendable retrieval accuracy. For instance, models like DeepCS invariably fix the final representation vector dimension at 512, meaning that the similarity computation between a code and query vector demands 512 multiplications and 512 additions with double data type variables for each pair. The total calculation for a single linear scan of a corpus with 1 million code snippets is staggering, encompassing around 1 billion multiplications and additions. The situation is further exacerbated by approaches utilizing binary classification, which, although absolve the need for pre-storage of representation vectors, necessitate real-time inference of target token sequences alongside all description token sequences for every retrieval. This real-time requirement considerably bloats the computational cost, given the hefty number of parameters in contemporary deep learning models. Moreover, models employing interaction mechanisms like TabCS and SANCS are compelled to interact with all code documents for each query, resulting in an astronomical computational cost. Nonetheless, IR methods can supply a small-scale set of candidate codes to neural ranking models, accelerating the retrieval process significantly. This expedited approach, however, has its accuracy tethered to the performance of the IR methods, thus illuminating the imperative for augmenting these methods.

Fig. 1

The left figure depicts an Accuracy/Efficiency Map juxtaposing various code search models against their ExCS-enhanced versions. The diagram underlines the equilibrium between MRR and search speed, spotlighting the potential of assimilating ExCS to optimize both efficiency and accuracy in code search. And the right figure shows an example of code expansion.

Against this backdrop, we put forth CodeEx, an innovative sequence-to-sequence model crafted to alleviate the “vocabulary mismatch” dilemma. Envisioned as a question-answering mechanism, CodeEx predicts plausible queries for a given code and spawns corresponding expansions, thereby enriching the semantic association between code and queries. This nuanced tactic not only facilitates a more potent bridging of the semantic gap but also elevates the accuracy of IR methods, enabling them to furnish more reliable candidate codes to the succeeding neural ranking models, thereby forging a synergistic framework for advanced code search.

When dealing with large codebases, such as those on GitHub, it is only practical to use IR methods for code search¹⁴. To address this, we introduce ExCS, a groundbreaking code search tool that combines CodeEx with IR to enhance the efficiency of existing deep learning methods. ExCS scales on the initial search by leveraging IR methods. ExCS then applies deep learning models exclusively for re-ranking the shortlisted candidates, merging the efficiency of IR with the precision of neural models. This approach makes the search process both practical and scalable, even in extensive codebases. In its offline stage, ExCS utilizes CodeEx to generate code expansions from the code corpus, indexing the keywords from these expansions. During the online phase, ExCS leverages IR to extract the code candidates, which are then re-ranked using neural ranking models. This strategy keeps the time cost of deep learning-based code search within a manageable range while maintaining accuracy. Figure 1 clearly demonstrates the positive impact of ExCS on various code search methods. By comparing standard models with their ExCS-enhanced versions, the graph illustrates the balance between Mean Reciprocal Rank (MRR) and search speed, highlighting how ExCS improves both efficiency and accuracy in code search. Our contributions are encapsulated as follows:

• We unveil a unique deep neural network, CodeEx, aimed at enriching code with pertinent natural language (NL) sequences by anticipating likely queries.

• We engineer ExCS, a tool that capitalizes on CodeEx and IR to refine the efficiency of prevailing deep learning-based methods.

• We undertake a comprehensive experimental evaluation on public benchmarks, demonstrating that ExCS substantially uplifts retrieval efficiency while maintaining comparable accuracy to baseline models, thus marking a significant stride towards resolving the efficiency-accuracy trade-off in code search.

Background and motivation

Code search

Code search aims to remedy the semantic disconnection between queries in Natural Language (NL) and codes in the programming language. The so-called semantic gap originates from the “vocabulary mismatch” in discrete thermal representation and far distance in continuous vector representation. Various code search methods have been proposed^{6,7,9,15,16,17,18,19,20,21,22,23} to address this issue. Early methods^16,22,23 employed Information Retrieval (IR) techniques to return results aligned with the query intent. They tackled the issue by enhancing the query with related keywords. For example, CodeHow, a state-of-the-art IR-based model, utilizes related APIs to expand user queries and improve query results. Although deep learning’s assistance is absent in these approaches, they compensate with the maturity and variety of methodologies and techniques from the field of IR²⁴. Nonetheless, as we discussed, IR alone is insufficient in bridging the semantic gap between code and NL¹.

With the surge of deep learning, numerous methods have integrated it into code search. Such models frequently utilize the common technique of joint embedding^25,26,27, which collectively embeds diverse data types into a unified vector space, causing semantically similar concepts (across different modalities) to cluster in nearby regions of the vector space. According to²⁸, code search models are of two types, based on their architecture—siamese²⁹ and interaction-based. In the siamese type, codes and queries are processed independently. Gu et al.⁷ were the pioneers in introducing deep learning to code search, proposing DeepCS which embeds code and query into vectors through LSTM. Other models under this type also leverage Language Models (LMs) due to their simplicity. On the other hand, interaction-based models, such as CARLCS-CNN⁹ and TabCS¹⁸, generate an interaction matrix to evaluate the relevance between the representations of query and code. For instance, CARLCS-CNN uses convolutional neural networks and LSTM to learn code and query embedding. With self-attention³⁰ gaining widespread usage in the NLP field, TAB-CS has incorporated a self-attention mechanism to embed code and query. Similarly, SAN-CS¹⁹ applies a global-attention mechanism to map the relationship between code and query. Notably, all the state-of-the-art models use interaction-based methods, effectively bridging the semantic gap between codes and queries.

Recent developments have introduced Large Language Models (LLMs) like StarCoder³¹, which use extensive pre-training and fine-tuning to help with code search and code generation tasks. Another notable LLM is Code Llama³², which helps with coding tasks by understanding natural language queries and providing related code snippets. The large number of parameters and extensive training data in these LLMs help them understand the subtle meanings between code and natural language, which is key to addressing the vocabulary mismatch problem. However, these models work in a generative way³³. So, when users use these LLMs for code search, it’s more like they are doing code generation. A more practical way of code search, similar to what’s done in AutoGPT³⁴, is to use search tools like Google or the vector library in Langchain³⁵ to find related content on web pages, which is then given to the LLMs for further processing. This way, the performance of the search tools also affects how well code search works with LLMs.

Efficiency in code search

In the spirit of detail, we shall analyze the time-consuming-operations in code search. The search methods previously discussed fall into two categories - those based on IR and those based on deep learning, which can further be classified by whether they incorporate an interaction mechanism. In IR-based code search, the principal time-consuming operations include computing the similarity score between query q and code document set ${\textbf {D}}=[d_1,...,d_n]$, and sorting to return the top-k results. BM25 is the commonly used approach to calculate scores. Following the similarity calculation:

$$\begin{aligned} Score(q,d)=\displaystyle \sum _{t\in Q}log[\frac{N}{df_{t}}] \cdot S(q_i,d) \cdot \frac{(k_1+1)tf_{tq}}{k_1+tf_{tq}} \end{aligned}$$

(1)

$$\begin{aligned} S(q_i,d)=\frac{(k_2+1)tf_{td}}{k_2[(1-b)+b\times (L_d/L_{ave})]+tf_{td}}, \end{aligned}$$

(2)

where d is a document in ${\textbf {D}}$, N is the number of documents in ${\textbf {D}}$, $df_t$is the number of documents that contain term t, $k_1$ and $k_2$ are fixed parameters, $tf_ {xy}$ denotes the number of occurrences of x in y and $L_ d$ is the length of the corresponding document d. $L_ {ave}$ is the average length of all documents. The time complexity of BM25 is:

$$\begin{aligned} O(BM25)=O(|q|\cdot |{\textbf {D}}|\cdot |{\textbf {T}}|), \end{aligned}$$

(3)

where $|\cdot |$ is the mod function, ${\textbf {T}}$ is the set of entities in the vocabulary of code document set ${\textbf {D}}$. It is necessary to sort the similarity scores to obtain the top-k list. Because all code search methods require this step, we use the universal quicksort in reordering, with a time complexity of O(nlogn).

For siamese model, codes and queries are processed independently, so the time-consuming operations for searching encompass embedding the query q, computing the cosine similarity between the query embedding ${\textbf {q}}$ and the stored code embedding set ${\textbf {C}}=[{\textbf {c}}_{\textbf {1}}, \ldots ,{\textbf {c}}_{\textbf {n}}]$ that had been previously calculated and stored during the offline phase, and finally sorting to return the top-k result list. Embedding queries depend on the embedding models. For example, the time complexity of widely-used LSTM and self-attention are calculated as follows:

$$\begin{aligned} O(LSTM) = O(|q|\cdot |{\textbf {q}}|^2) \end{aligned}$$

(4)

$$\begin{aligned} O(Self-attention) = O(|q|^2\cdot |{\textbf {q}}|) \end{aligned}$$

(5)

For the query q is usually much shorter than embedding size $|{\textbf {q}}|$, LSTM takes longer embedding time than self-attention. Then, the formula for calculating cosine similarity and the search time complexity is as follows:

$$\begin{aligned} CosSimilarity({\textbf {q}},{\textbf {c}})= & \frac{{\textbf {q}}\cdot {\textbf {c}}}{||{\textbf {q}}||\cdot ||{\textbf {c}}||} \end{aligned}$$

(6)

$$\begin{aligned} O(CosSimilarity)= & O(|{\textbf {q}}|\cdot |{\textbf {d}}|) \end{aligned}$$

(7)

$$\begin{aligned} O(Search_{siamese})= & O(|{\textbf {C}}|\cdot |{\textbf {q}}|\cdot |{\textbf {d}}|) \end{aligned}$$

(8)

Interaction-based models, on the other hand, necessitate three steps: jointly embedding codes and queries, calculating similarity, and sorting. However, as code representations must be calculated through joint embedding at search time, the embedding step cannot be deferred, unlike in siamese models. The time complexity of jointly embedding depends on the embedding models like (4) and (5). The similarity calculation is the same as (67). The search time complexity is as follows:

$$\begin{aligned} O(search_{interaction})=O(|{\textbf {C}}|\cdot |{\textbf {q}}|\cdot |{\textbf {d}}|\cdot {Emb}), \end{aligned}$$

(9)

where Emb is the dimension of the jointly embedding time complexity.

Fig. 2

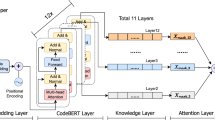
The overall structure of CodeEx is illustrated using a Java code script as an example. In the upper part, the overall expansion process involves passing the code through an encoder-decoder structure to obtain a semantic expansion for the term ’play voice.’ Utilizing global attention during this expansion, CodeEx extracts keywords from the code snippet and performs a homonym search to further expand these keywords. Finally, the two expansions are combined to produce the complete code expansion.

Motivation

The previous sections demonstrate that evaluating every piece of code against a query can significantly enhance the effectiveness of code search. However, this approach is impractical when dealing with large codebases, such as those found on GitHub. Our objective is to accelerate this process by reducing the amount of code that needs to be examined. By doing so, we can leverage powerful yet computationally intensive neural networks to re-rank a smaller set of code snippets initially identified by a term-based search engine.

To achieve this, we focus on improving how code is represented before it is indexed-using language models, for example, to better capture the semantic meaning of the code. This allows us to maintain the efficiency of the initial term-based search while enhancing its ability to retrieve relevant code snippets. The retrieved results can then be re-ranked by a more advanced neural ranking model, such as SANCS, to ensure accuracy.

This two-step method-first rapidly identifying a smaller set of potential matches and then re-ranking them for precision-aims to strike a balance between speed and accuracy, which is crucial for practical code search tools. This approach is particularly beneficial for large codebases, where scanning all the code for each query would be prohibitively time-consuming. By implementing this method, we aim to accelerate the code search process while maintaining or even improving the accuracy of the results, making code search more practical and effective for real-world software development scenarios.

Methods

In this section, we introduce the proposed code expansion model, CodeEx, and the related code search tool, ExCS. The following subsections present the method details. Specifically, Section III-B describes the details of CodeEx, and Section III-C describes the two stages of the proposed ExCS.

CodeEx

Inspired by document expansion, we propose a fine-tuned code expansion model named CodeEx (Code Expansion). Figure 2 illustrates the overall structure of CodeEx. CodeEx expands the code using two approaches: overall expansion and keyword expansion. Formally, for a given code $c$, the process is denoted as follows:

$$\begin{aligned} E = RD([E_o : E_k]), \end{aligned}$$

(10)

where $E$ is the output expansion of CodeEx, $E_o$ is the expansion generated by overall expansion, and $E_k$ is the expansion generated by keyword expansion. $RD()$ is the function that removes repeated terms in the sequence to shorten the expansion length.

Recently many state-of-the-art natural language processing LMs have been adapted to code while their computation costs are impractical on online code retrieval. However, CodeEx can perform term representation with LMs in the offline stage to save the time costs of the online stage. Since these two approaches are sequence-to-sequence tasks, we take them as downstream tasks of an encoder-decoder LM on code, CodeT5. CodeT5 leverages a state-of-the-art LM, T5, to pre-train an identifier-aware code understanding network. Compared to encoder-only models, like CodeBert, and decoder-only models, like PolyCoder, CodeT5 performs better generation tasks thanks to its encoder-decoder structure. The following subsections describe the detailed design of these modules.

• (1) Overall expansion

Overall expansion is a cross-modal sequence-to-sequence task aimed at obtaining the NL (Natural Language) sequences that match the input code semantics. Overall expansion takes the entire code tokens as input and outputs sequential tokens.

For fine-tuning, we adopt CodeT5 for the overall expansion task. As depicted in Fig. 3, the input to CodeT5 is a sequence of tokens. We first utilize tree-sitter to extract the annotations as labels and tokenize the code snippets following the implementation in CodeT5. Then, we input each code with a delimiter token as $input = ([CLS], c_1, \ldots , c_n)$, where $c_n$ represents the tokens in the code. We also adopt the beam search algorithm³⁶, to keep the top-B best hypotheses at each time step $t$, where $B$ is the beam size. With beam search, we obtain the top-k possible generations. We concatenate the generations and remove the duplicated tokens as output, denoted as follows:

$$\begin{aligned} \begin{aligned}&[s_1: \ldots : s_k] = Sample(CodeT5(c), k)\\&E_o = [s_1: \ldots : s_n ], \end{aligned} \end{aligned}$$

(11)

where $Sample$ is the function to return the top-k possible generation samples, and $s_k$ represents the $k$th possible sample.

• (2) Keyword expansion

Keyword expansion aims to supplement the overall expansion from the perspective of code tokens, which means keyword expansion is a code-to-code task. In contrast, overall expansion is a code-to-NL (Natural Language) task. As discussed in Section ii-C, method name, variable name, and API are artificially defined, although they are code features, making them more like NL. These features are essential because they are usually mentioned in the query. Compared to overall expansion, which generally summarizes these features in one word, keyword expansion tends to retain the variety of code features. The keyword refers to the tokens in the code that are semantically related to the query, such as the method name, API name, and variable name. The keyword expansion comprises two steps: keyword extraction and homonym search.

Keyword extraction

Initially, we extract all method names, API names, and variable names from the code tokens. Then, after the decoding of the overall expansion, we calculate the relation score between the above tokens ${\textbf {T}}=[t_1,...,t_n]$ and the first sample $s_1$ using a global-attention mechanism as follows:

$$\begin{aligned} \begin{aligned}&Q_t = {\textbf {t}}_{\textbf {n}}\cdot {W_Q},\\&K_s = {\textbf {s}}_{\textbf {1}}\cdot {W_K},\\&R = \sum (\text {softmax}(\frac{Q_t\cdot {K_s^T}}{\sqrt{d}})), \end{aligned} \end{aligned}$$

(12)

where ${\textbf {t}}_{\textbf {n}}$ and ${\textbf {s}}_{\textbf {1}}$ are the representation vectors learned from the overall expansion of $t_n$ and $s_1$, $W_Q$ and $W_K$ are the weighted matrices, $Q_t$ and $K_s$ are the feature matrices of $t_n$ and $s_1$, $\text {softmax}()$ is the softmax function, and $\sum ()$ is a function that summarizes the items. $R$ reflects how much the token is related to the generation. We select the top-k tokens above a threshold value as the keywords.

Homonym search

Subsequently, we identify the homonyms of the keywords. For the terms in the code vocabulary, we represent them in vectors using the encoder model. According to word2vec³⁷, the vectors represent the semantics of each term, and the distance between two vectors can reflect their semantic similarity. For the keywords, we find the top-k closest terms, also known as the homonyms, to expand the code.

For the loss function, we aim for the output to cover more terms in the query while maintaining grammatical correctness, thus we use a fused loss of cross-entropy and BLEU-N as the training objective. We adopt a multi-task approach. The loss function of a training sample is calculated as follows:

$$\begin{aligned} L_1= & BLEU-N(o, l) = BP \cdot \exp \left( \sum _{n=1}^{N} \omega _n \log p_n \right) , \end{aligned}$$

(13)

$$\begin{aligned} L_2= & \text {CrossEntropy}(o, l), \end{aligned}$$

(14)

$$\begin{aligned} L= & k_1 \cdot L_1 + k_2 \cdot L_2 , \end{aligned}$$

(15)

where $p_n$ is the precision score of the n-gram matches between output $o$ and label $l$, $BP$ is the brevity penalty, and $\omega _n$ is the uniform weight $\frac{1}{N}$. $\text {CrossEntropy}()$ is the cross-entropy loss function. $L_1$, $L_2$, and $L$ are the first, second, and final loss, and $k_1$ and $k_2$ are the hyperparameters.

In this section, we’ve provided a detailed methodology for our proposed CodeEx model and ExCS tool. The subsequent sections will delve into the implementation and evaluation of these methodologies.

ExCS

Figure 3 depicts the overall framework of ExCS which implements code search through offline and online stages. The offline stage utilizes CodeEx to generate code expansions for each code in the corpus respectively and indexes the expanded codes. The online stage comprises two steps: obtaining candidate codes via Information Retrieval (IR) methods, and re-ranking the candidates utilizing neural ranking models. Upon receiving a user query, ExCS initially employs the term-based IR method BM25 on the stored indexes to retrieve a ranked list of codes. Lastly, ExCS re-ranks the codes using neural ranking models.

• (1) Offline stage

In the offline stage, ExCS stores the indexes of expanded codes and the code embedding for Siamese neural ranking models. Initially, ExCS applies CodeEx on the code stored in the corpus to obtain expanded codes $\hat{\varvec{C}}$. The expansions are placed as annotations at the beginning of the code snippets since annotations can enrich the code semantics without altering the code structure. Following this, we filter the expanded codes by removing stop words and operations in Java, like “if”, as these terms are not beneficial when the query is in Natural Language (NL), and as per (1), longer documents result in lower BM25 scores. A simple experiment showed that term-based IR methods perform better on the filtered codes. After filtering, we obtain the final code documents $\overline{\varvec{C}} = [\overline{c}_1,...,\overline{c}_n]$.

For the Siamese neural ranking models, like DeepCS, ExCS will embed the codes during the offline stage using the code encoder in the model. For instance, in DeepCS, three features are extracted from a code $c$: method name (a list of camel split tokens), API sequence (a list of API words in the method body), and tokens (a bag of words in the method body and annotation). DeepCS embeds the method name $\varvec{M}=[m_1,...,m_n]$ and API sequence $\varvec{A}=[a_1,...,a_n]$ with LSTM, and embeds the tokens $\varvec{T}=[t_1,...,t_n]$ with MLP. The vectors of the three features are then fused into one vector $\varvec{c}$ as follows:

$$\begin{aligned} \begin{aligned}&\varvec{m} = LSTM_m(\varvec{M}), \\&\varvec{a} = LSTM_a(\varvec{A}), \\&\varvec{t} = MLP_c(\varvec{T}), \\&\varvec{c} = \tanh (MLP_{\text {fuse}}([\varvec{m};\varvec{a};\varvec{t}])), \end{aligned} \end{aligned}$$

(16)

where $\varvec{m}, \varvec{a}, \varvec{t}$ are the embedded vectors of $\varvec{M}, \varvec{A}, \varvec{T}$, $\tanh ()$ is the activation function, and $[\varvec{m};\varvec{a};\varvec{t}]$ represents the concatenation of the three vectors.

Following code embedding, we store the code documents as $d=\{``code'': \overline{c}, ``code embedding'': \varvec{c}\}$, where $\overline{c}$ is the filtered code. For interaction-based models, like SANCS, we simply store the code document as $d_t=\{``code'': \overline{c}\}$. The code documents are then indexed and stored.

Fig. 3

This picture depicts two methods of code search. The top part illustrates the common practice where, in the offline phase, code is pre-processed and stored in a database. During the online phase, the database and query are inputted into a nueral ranking model for searching. On the other hand, the bottom part illustrates the ExCS method where, in the offline phase, code is processed through CodeEX to generate Code Expansion. Then index them and store the indexes in an index database. During the online phase, the query is first processed through IR methods in the index database to retrieve candidates. Subsequently, the query and candidates are inputted into the ranking model for searching.

• (2) Online stage

When a developer submits a NL query $q$, the online stage follows two steps: IR-based filtering, and deep learning-based re-ranking.

IR-based filtering

Initially, ExCS performs a code search with BM25 on the codebase, selecting the top-k results as candidates and obtaining the relevant code documents $\varvec{C_k}=[c_k^1,...,c_k^k]$.

Deep learning-based re-ranking

Upon obtaining $\varvec{C_k}$, we regard it as a new, albeit smaller, codebase to execute neural ranking models on it.

For the Siamese neural ranking models, the code representation $\varvec{c}$ has already been stored in the code document. Hence ExCS needs to embed the query $q$ into vector $\varvec{q}$, denoted as follows:

$$\begin{aligned} \varvec{q} = W_q \cdot q, \end{aligned}$$

(17)

where $W_q$ is the matrix of query encoder parameters of the neural ranking models. Subsequently, the re-ranking process calculates the cosine similarity between the query vector $\varvec{q}$ and the candidate code vectors $[\varvec{c_k^1},...,\varvec{c_k^k}]$ respectively, and sorts the candidates to return the result list.

For interaction-based models, ExCS first constructs a data loader with the three code features: method name, API sequence, and tokens. Models like TabCS and SANCS initially embed the code features into vectors using self-attention, respectively, and fuse them into a code feature matrix $\varvec{C}$ prior to the interaction mechanism, denoted as follows:

$$\begin{aligned} \begin{aligned}&\varvec{m} = \text {SelfAtt}_m(\varvec{M}), \\&\varvec{a} = \text {SelfAtt}_a(\varvec{A}), \\&\varvec{t} = \text {SelfAtt}_c(\varvec{T}), \\&\varvec{C} = [\varvec{m};\varvec{a};\varvec{t}], \end{aligned} \end{aligned}$$

(18)

Then, these models leverage interaction-based mechanisms to attain further representations of code and query, and calculate the similarity. For instance, TabCS employs a fuse matrix $\varvec{F}$ to fuse the representations as follows:

$$\begin{aligned} \begin{aligned}&\varvec{F} = \tanh (C^TU\varvec{q}),\\&\varvec{\tilde{c}} = MLP_{\varvec{\tilde{c}}}(\text {maxpooling}(F)),\\&\varvec{\tilde{q}} = MLP_{\varvec{\tilde{q}}}(\text {maxpooling}(F^T)),\\&\text {sim} = \cos (\varvec{\tilde{c}}, \varvec{\tilde{q}}),\\ \end{aligned} \end{aligned}$$

(19)

where $\varvec{\tilde{c}}$ and $\varvec{\tilde{q}}$ are the new vectors of code and query after interaction.

Finally, the models recommend a code list wherein the $k$th code is the $k$th possibly corresponding code for the query. This structured approach facilitates a streamlined process from query input to code recommendation, ensuring that the most relevant code snippets are effectively retrieved and ranked according to their relevance to the given query.

Experiment

This section delineates the research questions(RQs) under investigation, the baseline models chosen for comparison, the evaluation metrics employed, and the experimental setup and results.

Research questions

The core focus of our experiments revolves around the following RQs:

• RQ1: Can our proposed method, ExCS, enhance model accuracy and efficiency?

     RQ1 examines the performance enhancement of each baseline model post adaptation to ExCS. The baseline models are elucidated in the ensuing section.

• RQ2: What impact do different components of ExCS have on accuracy?

     ExCS incorporates various elements such as the number of candidates pre-re-ranking, the length of code expansion, and the incorporation of new words and copied words in code expansion, which are pivotal in code search. We orchestrate comparative experiments adjusting these parameters to discern their influence on model accuracy and to ascertain the optimal settings.

• RQ3: How does ExCS augment efficiency?

     RQ3 delves into the time expenditure across different code search phases. Given that ExCS impacts similar model types uniformly, we select the best-performing models from the Siamese network and interaction-based network categories, namely DeepCS and SANCS, for experimentation. We juxtapose the time cost pre and post ExCS utilization to gauge the efficiency enhancement rendered by ExCS.

Baselines

The baseline models, selected from state-of-the-art neural ranking models, are categorized based on their structure and deep learning methodologies.

BM25: BM25, a pivotal ranking function in Information Retrieval (IR), excels in ranking documents in large text collections. Utilizing the Anserini open-source IR toolkit, we harness BM25’s prowess for document indexing in our experiment²⁸.

DeepCS: DeepCS employs a Siamese network and joint embedding to facilitate effective code retrieval, applying RNN to method names, API sequences, and MLP on code tokens to generate representative vectors for both code and queries.

CARLCS-CNN: CARLCS-CNN, an interaction-based code search model, employs LSTM and CNN for individual code and query embedding before leveraging a fusion matrix to derive interdependent representations, fostering nuanced code-query relationships.

TabCS: TabCS, with its two-stage Attention-based network, extracts code and query semantics individually, then employs a co-attention mechanism, akin to CARLCS-CNN, to discern semantic correlation between code and query, enhancing code search accuracy.

SANCS: SANCS leverages self-attention networks to construct a comprehensive code-description network and a method for code and description representation along with a similarity measure module, providing a nuanced representation of code and queries.

Evaluation metrics

To meticulously evaluate model accuracy, we adopt two widely acknowledged metrics, namely SuccessRate and Mean Reciprocal Rank (MRR), following the methodology proposed by Xu et al.¹⁸.

SuccessRate@k(SR@k), the proportion of queries in which the relevant code answer can be found in the top-k result list, is computed as follows:

$$\begin{aligned} SuccessRate@k=\frac{1}{|Q|}\displaystyle \sum ^{|Q|}_{i=1}\delta (FRank_{Q_i}\le {k}), \end{aligned}$$

(20)

where Q is the query set in the evaluation and $FRank_{Q_i}$ is the rank of the relevant answer for the ith query in Q. $\delta$ is an indicator function that returns 1 when the $FRank_{Q_i}$ is within the top k returning results. Otherwise, it returns 0.

MRR, the average of the reciprocal ranks of the first hit results¹² of a set of queries Q, is calculated as follows:

$$\begin{aligned} MRR=\frac{1}{|Q|}\displaystyle \sum ^{|Q|}_{i=1}\frac{1}{FRank_{Q_i}}, \end{aligned}$$

(21)

For the model efficiency, we employ the average search time as a metric.

Average Search Time, the average time spent from entering a query to getting the result list, measured in milliseconds per query (ms/query), provides a tangible measure of efficiency.

Dataset

We conduct our Experiments on the java dataset provided by CodeSearchNet(CSN)³⁸. CSN is a collection of datasets and benchmarks for semantic code retrieval. The datasets generated and/or analysed during the current study are available in the code_search_net repository, https://huggingface.co/datasets/code_search_net. It extracts functions and their paired comments from GitHub repositories. It covers six programming languages, and we elect to use the training dataset for Java, which encompasses 394,471 data points. Following the implementation blueprint by Sun et al.³⁹, we filter the dataset to eliminate repeat and poor-quality data, resulting in a refined dataset of 192,031 data points for training. The evaluation and test data remain unaltered from CSN, comprising 4009 and 26909 data points, respectively.

Model configuration

We conduct fine-tuning on the codet5 base multi sum (220 m) variant of CodeT5 [13] from Huggingface to realize CodeEx. For the overall expansion, we set the maximum source and target sequence lengths to 128 and 16, respectively. The batch size is set to 16, and a peak learning rate of 2e-4 with linear attenuation is adopted. We aim to obtain the top-5 samples and employ BLEU-1 for the loss function as per equation (15). For the keyword expansion, the top 5 keywords are selected. The pre-training regimen is executed on four Nvidia Tesla V100 clusters, each with 16G memory. The entire training duration for fine-tuning spans three days.

Results

This section delves into the examination of the three RQs outlined in Sect "Research questions".

RQ1: Performance Evaluation of ExCS in Terms of Accuracy and Efficiency

Table 1 provides a comparative analysis concerning the accuracy and efficiency between the baseline code search models described in Section III and their corresponding adaptations with ExCS. The term “BM25+CodeEx” denotes the IR-based filtering component during the offline stage in ExCS. Symbols “$\uparrow$” and “$\downarrow$” denote an increase or decrease in the metric when ExCS is integrated with the baseline model, respectively, with the following percentages indicating the extent of change relative to the baseline models.

Table 1 Model effectiveness and model efficiency without and with ExCS.

The model efficiency is notably enhanced, with the average search time being reduced to under 100 ms/query when the neural ranking models are adapted to ExCS. This results in an average acceleration of 87.0% in comparison to the baseline models. This efficiency boost is attributed to the neural ranking models operating on a narrowed down codebase of 1000 entries, which significantly reduces the retrieval time. The BM25+CodeEx component accounts for approximately 80% of the time spent processing the large-scale codebase to generate candidates.

In terms of model accuracy, the fundamental component of ExCS, BM25+CodeEx, exhibits a 4.77% decrement in SR@1 performance while showcasing a significant enhancement of 19.07%/37.53% in SR@5 and SR@10 performance compared to MRR. In contrast, other methods exhibit an average increment of 2.39%/20.80%/38.68% in SR@1, SR@5, and SR@10 compared to MRR. The decrement in SR@1 is reasoned to be due to the expansion terms not present in the query, which diminishes the similarity measure between the correct code and the query. As the expansion increases the code document length and for other code documents, the expansion adds related terms to the query. According to (1), the longer the document and the more frequent the term showing in other documents will decrease the BM25. So the possibility of the correct answer showing in the first place decreases while the SR in a range remains normal. Also, We find that BM25+CodeEx outperforms DeepCS by 4.7%/3.3%/1.7%/11.0% in terms of SR@1/5/10, and MRR. This result shows that even without neural re-reranking, the IR-based search method can also get good accuracy with CodeEx.

For the baseline neural ranking models, the results demonstrate that the ExCS can preserve the accuracy or even improve the accuracy of the baseline models. For DeepCS, ExCS with DeepCS outperforms the baseline model by 14.2%/15.2%/14.1%/15.0% in SR@1/5/10, and MRR. The increment in accuracy is mainly due to the semantic enrichment by the expansion. By adding NL expansion, although DeepCS is based on the siamese network and LSTM is not as powerful as self-attention, DeepCS can get the semantic relationship between query and codes. For CARLCS-CNN, ExCS with CARLCS-CNN outperforms the baseline model by 11.5%/13.3%/12.1%/10.3% in SR@1/5/10, and MRR. The increment decreases by an average of 25.2% compared to DeepCS. It is because the CARLCS-CNN has an interaction mechanism, which reduces the additional advantage of enriched codes. For TabCS, ExCS with TabCS outperforms the baseline model by 0.5%/0.5%/0.6%/0.7% in terms of SR@1/5/10, and MRR. The increment becomes relatively smaller than above. We can find that the better the code query relationship capture is the baseline model, the less the code expansion can help improve the accuracy. For SANCS, ExCS with DeepCS underperforms the baseline model by 1.1%/2.2%/1.2%/1.1% in SR@1/5/10, and MRR. The accuracy decreases with ExCS. It is due to the candidates can not cover all the correct codes. So the advantage of semantic enrichment is less than the disadvantage of not having all the correct codes in candidates. Since ExCS must first use IR methods for the initial search to be applicable to large-scale codebases, the more precise the retrieval model, the greater the accuracy loss during this step. However, more precise models often require larger parameter counts or additional interaction mechanisms, which means they take longer to execute. Therefore, ExCS offers a trade-off where some accuracy is sacrificed to make the model usable.

Fig. 4

Composite figure of various comparisons.

RQ2: Analyzing the Impact of Different Components of ExCS on Effectiveness

This subsection conducts a series of controlled experiments to dissect the influence of different components within ExCS-namely, the number of candidates pre-re-ranking, the extent of code expansion, and the distribution of new versus copied words in the code expansion. Given DeepCS’s sensitivity to the alterations in the accuracy of BM25+CodeEx and the expansion, it was chosen as the baseline model for this segment of the analysis.

For the number of candidates, it affects the posibiliry the correct code be covered in the candidates and the time cost of the neural re-ranking. Figure 4a shows the Recall@k of the BM25+CodeEx, where k is the number of candidates and Recall@k represents the proportion of the number of correct documents in the top-k results to the number of all documents. We can find the Recall@k increases rapidly from 0.738 to 0.925 from 100 to 1000, and the increment goes slow from 0.925 to 0.989 from 1000 to 10,000. It is due to when k gets bigger, more correct codes with relatively low BM25 will be covered. However, when more correct codes are covered, the rest correct codes have a more negligible correlation to the query, in which case, we need to set way bigger k to obtain little correct codes. From Fig. 4b, we find the trend of MRR of ExCS with DeepCS is like the trend in Fig. 4a. It is because the accuracy of ExCS with DeepCS mainly relies on the Recall@k of the BM25+CodeEx while the semantic enrichment is the same. Figure 4c shows the average search time of the ExCS with DeepCS. We notice the time costs increase with the number of candidates increases. We argue that the time costs positively correlate to the scale of the codebase provided to DeepCS. From the above observation, considering accuracy and time cost, providing 1000 candidates is suitable for ExCS.

Then, we did a research on how the length of expansions affects the accuracy. We expanded the codes from 10 tokens to 100 tokens. The results are in Fig. 4d. From the we show some examples of expansions produced by the CodeEx. Alse we notice that CodeEx refer to copy some tokens from the input codes(e.g., video, url, extract). This shows that CodeEx can effectively re-weight the terms and gets the key terms. Nevertheless, CodeEx also produces tokens not in the input document(e.g. voice, audio). This terms are characterized by synonyms and other related terms.

Table 2 Model effectiveness and model efficiency without and with ExCS.

Table 3 Model accuracy on different type of expansion.

To quantify the above analysis, we measure the proportion of copied tokens and new tokens. In the test set, we find that 65% of the predictions are copied while 35% are new. We did ablation research and put results in Table 2. Expanding with copied terms outperforms the original documents MRR by 2.01% and new terms by 30.97%. We notice that the copied terms improve the performance less than the new terms. This is because the copied terms can only increase the term frequency of the tokens already in codes. In comparison, new terms can have more terms matching the query. Meanwhile, We achieve the highest MRR, 0.4527, with both types of terms, which shows that they are complementary.

RQ3: Efficiency Enhancement through ExCS

Table 3 provides a detailed breakdown of the time costs associated with embedding, vector similarity calculation, and array sorting processes across two state-of-the-art models, DeepCS and SANCS, as described in Sect "Baselines", juxtaposed against BM25+CodeEx. This evaluation was conducted under a consistent experimental environment. We rounded the average experimental data, and during retrieval, there are other time-consuming procedures like loading documents so that the total time will be different from Table 1.

The vector similarity calculation time cost depends on the dimension of the models, in which DeepCS is 512 and SANCS is 128, so SANCS is faster than DeepCS. However, when adapted to ExCS, the time cost mainly depends on the BM25. The array sorting time is nearly the same. We can find that ExCS contributes most to the embedding step. For DeepCS, by storing the code embeddings in advance, ExCS significantly saves the embedding time, for the LSTM can only be calculated serially. For SANCS, self-attention can be calculated fast in parallel on GPUs, and the co-attention mechanism is relatively simple. So when SANCS only needs to perform neural ranking on a small-scale codebase, SANCS is very fast.

Threats to Validity

This section elucidates potential threats to the validity of our findings and delineates the steps taken to mitigate them where possible.

External validity: External validity concerns the generalizability of our findings to other settings or populations.

• Generalizability: The models were assessed utilizing a specific dataset under controlled settings. The evaluation was rigorous, yet the extension of these results to other datasets or different settings warrants further exploration. Our work lays a robust foundation for such future investigations, aiming to ensure the adaptability and applicability of the proposed ExCS model across diverse scenarios.

• Dataset bias: The dataset employed in our evaluation may embody inherent biases, which is a common concern in machine learning endeavors. We have endeavored to choose a representative dataset, yet the performance metrics might vary with different datasets. It’s an inherent trade-off, yet it also sparks the avenue for evaluating the model’s performance across a spectrum of datasets.

Internal validity: Internal validity pertains to the integrity of the experimental design and the causal relationships inferred.

• Parameter tuning: The models’ performance is inherently tied to the choice of parameters. Our approach to parameter tuning was systematic and based on established practices, endeavoring to unveil the models’ potential. Yet, there could be alternative tuning approaches or parameter sets that might yield different results, signifying an area for further exploration.

• Implementation integrity: Although meticulous testing was conducted to ensure the correctness of the implementation, the complex nature of software systems could harbor unnoticed issues that might affect the results. We have shared our code to promote transparency and facilitate validation by the community.

Construct validity: Construct validity is concerned with the adequacy of the measurement instruments.

• Measurement metrics: The metrics employed for evaluating model performance are standard in the field. However, they may not encapsulate all facets of model effectiveness and efficiency. Future work could consider employing or developing alternative metrics that might offer a more holistic view of the model’s performance.

• Baseline comparisons: Our choice of baseline models was grounded on their relevance and common use in the field. Yet, the comparative analysis might exhibit different nuances with alternative baseline models or configurations. This aspect underscores the importance of continuous evaluation against emerging models and configurations.

Addressing these threats in a forthright manner not only underscores the robustness of our research process but also paves the way for future work. It invites the exploration of the proposed ExCS model across a broader spectrum of settings and against a wider array of baseline models. It also promotes the investigation of alternative parameter tuning strategies and performance metrics, all aimed at fostering a deeper and more comprehensive understanding of the model’s strengths, areas of improvement, and its potential impact on the field.

Conclusion and future works

We introduce ExCS to speed up code search, which combines CodeEx-based Information Retrieval (IR) methods and neural ranking models. ExCS uses a two-step approach common in the IR field to cut down the time needed by neural ranking models. It first quickly finds a small set of candidate codes using IR methods and then re-ranks these candidates with neural ranking models. Moreover, ExCS is easy to adapt to any neural ranking models by using them as re-rankers, significantly reducing their retrieval time cost. Our thorough experiments on Java datasets from CodeSearchNet (CSN) show that compared to traditional code search models, ExCS greatly improves retrieval efficiency while maintaining nearly the same performance.

For future work, we plan to address some challenges. Firstly, our experiments are only done on method-level Java datasets. We plan to include datasets from other languages in CSN. Secondly, the performance of ExCS heavily relies on the pre-trained models and the chosen dataset. Most datasets use the annotation as a query, which isn’t common in real-world situations. Therefore, we aim to collect manually marked data and realistic search data from sources like Google or Bing to test our method further in the future.