Introduction

Background

With the explosive growth of wireless communication applications and the continuous innovation and development of wireless communication technology1, the scarcity of spectrum resources and the increasingly complex electromagnetic environment have become great challenges for communication systems. The traditional spectrum management adopts a static allocation strategy, which is the main reason for low spectrum utilization2. The emergence of CR provides a new technological solution to significantly improve the efficiency of spectrum resource utilization3. It can monitor and understand the usage of spectrum in the current environment, allowing secondary users (SU) to access idle spectrum without causing interference to PUs. SS, as the primary component of CR systems, endows the system with the ability to discover spectrum holes. The detection performance of SS directly determines whether it can accurately and real-time discover idle spectrum, and then allocate suitable communication frequency bands for SUs. This key link profoundly affects the operational efficiency and quality of service of the entire wireless communication system4.

The characteristics of channel fading, environmental noise, and dynamic changes in wireless channels can seriously affect the performance of SS5. Among them, noise, as an important interference source, its complexity and diversity lead to a decline in the performance of traditional SS methods. In an ideal situation, many theoretical analyses and algorithm designs tend to assume that noise follows a Gaussian distribution. However, in real-world environments, transient electromagnetic interference caused by thunderstorms and lightning, short voltage spikes or current pulses caused by arcing and switching operations on power lines, do not follow a Gaussian distribution. These non-Gaussian noises have the characteristics of strong suddenness, short duration, and concentrated energy, which pose a serious challenge to SS. Therefore, in order to improve the accuracy and robustness of SS, it is necessary to develop sensing techniques and algorithms that can effectively deal with such noise. When modeling noise, several common empirical models are worth paying attention to. Gaussian mixture model (GMM) and GGD are widely used to fit the pulse phenomena of man-made impulsive noise and ultra wideband interference6,7,8,9,10. The \(\alpha\)-stable distribution has good fitting properties for natural electromagnetic noise environments11.

Research status

Traditional SS algorithms include energy detection (ED)12, matched filter detection (MFD)13, cyclostationary feature detection14 and so on. Specifically, the ED determines whether a particular frequency band is occupied by calculating the energy in that band compared to a threshold value. It is widely used due to the simplicity of its implementation, but it requires a high estimate of the noise power and performs poorly in low SNR conditions. In addition, the calculation of the threshold must be adjusted based on specific noise distributions, as the threshold calculation formulas for different noise distributions are incompatible with each other. Of particular importance is that traditional ED will lose its effectiveness due to the possible absence of second-order moments in the \(\alpha\)-stable distribution15. MDF utilizes known features of the PU signal to design a specific filter to match the received signal. It achieves maximum detection performance under ideal conditions, but requires a priori information about the PU, which is not always applicable in real environment. Cyclostationary feature detection determines the presence of a signal by detecting the periodic changes in the statistical characteristics of the signal. This method improves the performance of SS in low SNR environments, however, it has high computational complexity.

Machine learning and deep learning, as key technologies in the field of artificial intelligence, have been widely researched and applied in areas such as computer vision, natural language processing, and network security16,17,18,19,20. With the continuous maturity of deep learning technology, its application in the field of communication has become an increasingly hot research topic. Deep learning is completely data-driven and can automatically learn and extract the features of complex signals without any priori information, thereby improving the performance of SS. Gao et al.21 proposed DetectNet, a combined model of CNN, Long Short-Term Memory (LSTM), and Deep Neural Network (DNN) for SS. DetectNet capitalizes on the underlying structural information of modulated signals, showcasing state-of-the-art detection performance. Su et al.22 applied a stacked convolutional autoencoder to preprocess signals for noise reduction. They introduced a self-attention mechanism in a combined model named H-CSG, further enhancing detection performance. In references23,24, the authors used short-time Fourier transform and wavelet transform to process signal data into time-frequency matrix data as inputs to CNN, transforming the SS into an image classification problem. Wang et al.25 utilized ConvLSTM to simultaneously extract temporal and spatial features of IQ signals, and then implemented SS at extremely low SNR based on the extracted features. These deep learning based methods are effective in terms of results, which proves that deep learning has enormous potential for development in the field of SS. The above studies were conducted under the assumption of Gaussian white noise background and have not yet explored robustness in non-Gaussian noise environments. Mehrabian et al. proposed a CNN detector for symmetric \(\alpha\)-stable (\(S\alpha S\)) noise26. Compared with the baselines, this detector exhibits stronger robustness in dealing with impulse noise. Subsequently, they further proposed a CNN detector suitable for various noise models in multi antenna systems, including Middle Class A, \(S\alpha S\) distribution, and GGD27.

Motivation and contribution

The above research methods only use information from one domain in the signal as input to the neural network, ignoring the rich information contained in other domains. Therefore, these methods may not achieve optimal performance in non-Gaussian noise environments28. Due to the regularity exhibited by PU signals in the time domain and the transient nature of non-Gaussian noise pulses, using GRU to extract global temporal dependencies is very helpful. Furthermore, it is worth noting that frequency domain information also plays an important role in signal processing. Since frequency domain signals do not contain time series information, CNN is used to focus on local features in the frequency domain. Taking inspiration from the cross attention mechanism’s ability to effectively fuse multimodal features29,30, we have adopted this mechanism as a module for fusing time-domain and frequency-domain features. Through this integration, the TFCFN adapts to various noises and improves performance. The main contributions of this work are as follows:

  1. 1.

    In our experiments, we employ the open-source RadioML2016.10a dataset31 to represent PU signals. We further utilize a GGD noise model to simulate the non-Gaussian noise encountered in real communication environments, thereby training our model.

  2. 2.

    We propose a deep learning-based model that effectively fuses time and frequency features using a cross-attention mechanism to improve the accuracy of SS.

  3. 3.

    We conduct comparative experiments under varying degrees of noise tailing conditions to evaluate the performance differences between our proposed model and other methods such as ED32, DetectNet21, WT-ResNet24, ConvLSTM25, 1D-CNN26, 2D-CNN27, and MASSnet-B33. The experimental results indicate that our model exhibits superior detection performance and robustness, regardless of whether the noise tailing is mild or severe.

Organization

The rest of this paper is organized as follows. The “Related work” section introduces related work. The “System model” section introduces the system model and problem statement of SS. The proposed TFCFN and its training process are presented in the “The proposed TFCFN” section. The “Performance evaluation” section provides simulation results and discussion. Finally, the “Conclusion” section provides a summary of this paper. Table 1 provides the abbreviations and their descriptions used in this paper.

Table 1 Abbreviations and descriptions
Full size table

Related work

Traditional spectrum sensing methods

The ED12 algorithm has received widespread attention due to its simple implementation. Chen et al. proposed replacing the amplitude squared operation with an arbitrary positive power operation to improve the energy detector in Gaussian noise34. Fading and noise are key factors affecting the ED algorithm. Digham et al. proposed a closed form expression for the \(P_d\) on multipath channels35. Chatziantiou et al. derived an analytical expression for the average \(P_d\) under two wave with diffusion power fading, and extended it to collaborative SS and square law selection diversity reception to mitigate fading effects36. Gao et al. fully utilized the stochastic characteristics of the GGD and the central limit theorem to derive the \(P_d\) and \(P_f\), and analyzed the impact of noise uncertainty on the system32. The eigenvalue based methods are also popular in the field of SS. Chaurasiya et al. proposed a maximum-minimum-eigenvalue algorithm and a spectrum sensor architecture based on this algorithm37. In order to improve the detection performance under noise uncertainty, Hashim et al. obtained an adaptive threshold based on the absolute covariance value38. The method based on high-order moments is used for SS in satellite communication39. The hybrid SS technology proposed by Ramya et al. automatically selects sensing methods based on energy or eigenvalues according to the range of SNR40. MFD is a better detection algorithm when there is prior information of PU signal. Brito et al. proposed a hybrid method based on existing MFD, which flexibly adjusts the number of MFD used to optimize detection performance under different \(P_f\)41. Obtaining prior information limits the application in certain scenarios. The act of obtaining prior information limits its application in certain scenarios. To address this issue, Zhang et al. developed a new test statistic. This statistic is composed of the correlation between the received signal and its delayed version, as well as the independence of noise at different times. Due to the accumulation of correlation, prior information from PU is no longer required42. Bala et al. proposed an iterative algorithm applied to CR Internet of Things (IoT) devices to optimize sensing threshold and time, greatly improving CR-IoT throughput in low SNR regions43.

Deep learning-based spectrum sensing methods

Data driven deep learning methods have become a hot topic in the field of SS in recent years. An et al. proposed a CNN for digital television terrestrial multimedia broadcasting systems, which can achieve satisfactory \(P_d\) at low SNRs44. Duan et al. used kernel principal component analysis to map the sampled signal to a high-dimensional space, created a covariance matrix, and then obtained the eigenvectors through matrix decomposition. Finally, CNN was used for classification45. Uvaydov et al. implemented real-time wideband SS using CNN46. Based on this work, Mei et al. designed a parallel CNN that reduced latency47. Wang et al. used residual dense network to solve the problem of gradient vanishing in deep network structure, while using convolutional block attention module to improve network performance48. The LSTM model developed by Balwani et al. extracted temporal correlations between spectrum data and achieved high classification accuracy, but at the cost of longer training and execution time49. Subsequently, Soni et al. improved the detection performance by using PU activity statistics as training data for LSTM, at the cost of high time consumption50. Combining various models together can extract multiple features. Xing et al. used CNN and BiLSTM in series, simultaneously extracting local features and global correlations of time-domain data, and then emphasized the importance of features using self-attention51. Denoising the signal and then classifying it is a novel innovation. Due to the two-stage nature of the H-CSG method22, where the denoising and detection stages are trained separately, the results are affected by the denoising performance. Therefore, Su et al. implemented joint learning for denoising and detection.52. Ni et al. did not limit themselves to CNN and LSTM, but used a temporal convolutional network with a special structure that allows it to extract temporal related features from sequence data53. MASSnet adopts a residual network structure, which is specifically optimized for the flexible configuration problem of multi antenna technology33. The most popular transformer model in the natural language processing field is gradually being used to handle SS tasks54,55.

System model

In this work, we consider a single-input single-output (SISO) system influenced by Rayleigh fading channels and non-Gaussian noise. SS is used to detect the presence or absence of PU signals, so it is usually represented as a binary hypothesis problem:

$$\begin{aligned} r(n) = {\left\{ \begin{array}{ll} w(n), & H_0 \\ h(n)s(n) + w(n), & H_1 \end{array}\right. } \end{aligned}$$
(1)

where r(n) denotes the n-th received signal sample in a detection period; s(n) is the signal from the PU; h(n) represents the channel gain in the current detection period, and w(n) represents a random noise sequence that follows the GGD. \({H_0}\) and \({H_1}\) signify the hypotheses that the PU is absent and present, respectively.

The GGD can represent noise distributions with different heavy-tailed characteristics by adjusting its shape parameter, which is an extension of the Gaussian distribution and can adapt to a wider range of noise environments. Its probability density function (PDF) can be expressed as56:

$$\begin{aligned} f(x) = \frac{\beta }{2\alpha \Gamma (\frac{1}{\beta })}exp(-(\frac{|x|}{\alpha })^\beta ) \end{aligned}$$
(2)

where \({\beta }\) is the shape parameter, \({\Gamma (\cdot )}\) denotes gamma function, and \({\alpha }\) is the scale parameter and the relationship between it and the variance of the random variable can be expressed as: \({\sigma ^2} = \alpha ^2\frac{\Gamma (3/\beta )}{\Gamma (1/\beta )}\). In particular, when \({\beta =2}\), the GGD degenerates to a Gaussian distribution; when \({0<\beta <2}\), the GGD exhibits heavy-tailed properties.

Typically, the performance metrics for evaluating SS are \(P_d\) and \(P_d\) defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} P_d = P(H_1|H_1) \\ P_f = P(H_1|H_0) \end{array}\right. } \end{aligned}$$
(3)

where \({P_d}\) is the probability of correctly detecting PU signals in the presence of the PU, and \({P_f}\) is the probability of mistakenly identifying noise as a signal in the absence of the PU.

The proposed TFCFN

To effectively perform SS in a non-Gaussian noise environment, we have utilized a cross-attention mechanism to fuse time-domain and frequency-domain features, enabling the model to adaptively learn the correlations between time-frequency features and dynamically assign corresponding frequency-domain feature weights to each time-domain feature. In the following, we will introduce the generation and preprocessing method of the dataset, followed by the detailed parts of the TFCFN architecture, and finally, the training and testing process will be described.

Dataset generating and preprocessing

The RadioML2016.10a dataset is a publicly available dataset widely used for wireless signal modulation identification. We reconstructed this dataset to meet the needs of the SS task, which is represented as follows:

$$\begin{aligned} r_k = {\left\{ \begin{array}{ll} w_k, & H_0 \\ h_k \cdot s_k + w_k, & H_1\\ \end{array}\right. } \end{aligned}$$
(4)

where \({r_k}\) is the reconstructed signal, \({s_k}\) is the clean modulated signal, \({h_k}\) is the complex Rayleigh decay coefficient, and \({w_k}\) is the GGD noise. Specifically, we use clean QPSK signals with a signal length (L) of 128 and add GGD noise to simulate PU signals at specified SNRs. The SNR range we set spans from -20dB to 0dB, with an increment of 2dB. For each SNR level, we generate 2000 PU signal samples and an equivalent number of GGD noise samples. For the classification task, PU signal samples are labeled as 1, and GGD noise samples are labeled as 0. Therefore, the total number of signal samples in the entire dataset is 44000, with 22000 samples for \(H_0\) and \(H_1\) respectively. In addition, the dataset is divided into training set, validation set and test set in the ratio of 3:1:1. In the GGD, the variance of the noise is fixed to 1, and the shape parameter \({\beta }\) is selected from \(\{0.5, 1, 1.5,2\}\) to examine the effects of different noise trailing phenomena on the SS. Note that each \(\beta\) value builds a separate dataset.

The received signal is an IQ signal consisting of in-phase and quadrature components. As neural networks cannot process complex signals directly, the received IQ signal is decomposed into I-Q components, which can be represented by the \({L \times 2}\)-dimension matrix \({R_T}\) as follows:

$$\begin{aligned} R_T = [r_I(n); r_Q(n)] \end{aligned}$$
(5)

where L refers to the number of sampling points for a sample and \({r_I(n)}\), \({r_Q(n)}\) denote the I-Q components of the n-th received signal, respectively. And the dimensions of \(r_I(n)\) and \(r_Q(n)\) are both \(L\times 1\). The TFCFN needs to integrate information from both time and frequency domains to better understand and analyze the data. To obtain the frequency domain features, the TFCFN utilizes the Discrete Fourier Transform (DFT). The DFT converts a signal from the time domain to the frequency domain by decomposing it into a composite of different frequency components. Its formula is expressed as:

$$\begin{aligned} X[f] = \sum _{n=0}^{L-1}r[n]e^{-j\frac{2\pi fn}{N}} \end{aligned}$$
(6)

where X[f] denotes the complex amplitude in the frequency domain, and f denotes the different frequency components. Note that here r is equivalent to r(n) in Eq. (1) and r[n] represents the n-th sampling point. L refers to the number of sampling points for sample r. Specifically, the FFT is used to accomplish this transformation task. The resulting X[f] is complex vector, which needs to be processed as a matrix with \({L \times 2}\)-dimension:

$$\begin{aligned} R_F = [real(X[f]); imag(X[f])] \end{aligned}$$
(7)

where L represents the number of X[f] points, and its value is the same as the number of sampling points of r. The \(real(\cdot )\) and \(imag(\cdot )\) functions respectively refer to taking the real and imaginary parts.

In order to improve the performance and stability of the model,we perform max-min normalization on matrices \(R_T\) and \(R_F\) along the column-wise direction. By scaling the original data and mapping the features to the [0,1] interval, max-min normalization can effectively unify the magnitudes of different features, and it also helps to accelerate the learning process and improve the convergence speed of the model. The specific implementation is:

$$\begin{aligned} {\overline{R}} = \frac{R_{n, j} - min_{j}}{max_{j} - min_{j}} \end{aligned}$$
(8)

where \({\overline{R}}\) represents the matrix normalized by \(R_T\) or \(R_F\). \(R_{n, j}\) is the n-th element of the original matrix \(R_T\) or \(R_F\) in j-th column, \(min_{j}\) and \(max_{j}\) are the minimum and maximum values in j-th column, respectively. Finally, the normalized matrices of \(R_T\) and \(R_F\) are represented as \({\overline{R}}_T\) and \({\overline{R}}_F\), respectively.

TFCFN architecture

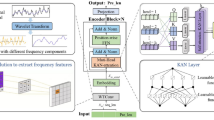
The TFCFN we designed is a multi-feature input model, and its overall architecture is shown in Fig. 1. As can be seen from the figure, the TFCFN is a deep neural network architecture that incorporate one-dimensional Convolutional (Conv1D) layers, GRUs, cross-attention block and Dense layers. The input time-domain and frequency-domain data are subjected to deep feature extraction using network modules appropriate to their characteristics, respectively; specifically, two GRUs are used to extract the time-domain features, and two Conv1D layers are used to extract the frequency features. Subsequently, the extracted features are fused using the cross-attention block to obtain a comprehensive feature representation being used for signal and noise classification. We denote the input time-domain and frequency-domain data as \({{\overline{R}}_T \in R^{L \times 2}}\) and \({{\overline{R}}_F \in R^{L \times 2}}\), respectively, where L denotes the signal length. In addition, Fig. 1 includes the settings of module parameters and changes in feature dimensions.

Fig. 1
figure 1

TFCFN architecture.

Full size image

Recurrent neural networks (RNN), particularly LSTM network, have been widely applied in SS tasks due to their exceptional ability to handle time-series data57,58,59. However, the structure of LSTM is relatively complex with a large number of parameters, leading to high computational costs. The GRU, as a simplified version of LSTM, merges the hidden state and cell state and contains only update and reset gates, thus simplifying the network structure. This simplification not only reduces the number of parameters in the model but also improves the efficiency of training, while maintaining performance comparable to LSTM60. Therefore, in our work, we have chosen to use two GRUs with 32 units to extract time features from the data, achieving a balance between performance and efficiency. The features extracted from the time-domain data are represented as \(X_t\). Frequency-domain data reveal information about the intensity and phase of the signal at different frequency components, which, although they do not contain underlying temporal information, are equally crucial for understanding the spectral properties of the signal. Conv1D excels at extracting local features of the data, which can help the model to identify the frequency-specific components as well as the interactions between these components. In order to deepen the model’s sensitivity to signal variations and to enhance the level of feature abstraction, we employ two Conv1D layers as the extraction module for frequency-domain features. The parameter configuration for these two Conv1D is “32@3”. This means that each layer contains 32 convolution kernels, with each kernel having a size of 3. After each convolutional layer, the data will undergo ReLU activation function processing to introduce nonlinear characteristics and enhance the feature extraction ability between layers. The features extracted from the frequency-domain data in this way are denoted as \(X_f\).

Fig. 2
figure 2

Cross-attention block.

Full size image

In recent years, the cross-attention mechanism has received extensive attention in the field of multimodal research. This mechanism is capable of computing the similarity between different modal input information and adaptingively associating and fusing the information based on the similarity scores. In this paper, we regard the frequency-domain and time-domain features as two modalities of the signal, each proving a different perspective on the signal. The application of the cross-attention mechanism in TFCFN is illustrated in the Fig. 2. Specifically, the features \(X_t\) and \(X_f\) are mapped into Query (Q), Key (K) and Value (V) matrices through Dense layer, and the Q and K matrices are dot products to generate an attention weight matrix whose elements represent the similarity between time-domain and frequency-domain features. In order to stabilize the gradient and prevent numerical overestimation, the dot product result is divided by \(\sqrt{d_k}\), where \(d_k\) is the diemnsion of K. Subsequently, the softmax function is applied to normalize these weights, resulting in an attention distribution assigned to the frequency-domain features on each time-domain features. The attention weight matrix is multiplied by the V matrix to obtain a feature representation X that combines time-domain and frequency-domain information. The calculation process is shown below:

$$\begin{aligned} X = Softmax(\frac{QK^T}{\sqrt{d_k}})V \end{aligned}$$
(9)

where T denotes transpose, and \(d_k\) is the dimension of K. In TFCFN, we combine early time-domain features with enhanced features to improve the model’s feature expression ability, and the final classification feature is represented as:

$$\begin{aligned} X' = X + X_d \end{aligned}$$
(10)

Subsequently, we further processed \(X'\) through a series of Conv1D and Dense layers to obtain the classification result. In the processing, in order to reduce the number of model parameters, we choose to use a Global Average Pooling layer instead of Flatten layer.

Training and testing phase

To train the TFCFN, we label the processed data according to the states of \({H_0}\) and \({H_1}\) to construct the training dataset:

$$\begin{aligned} {\mathcal {D}} = \{({\overline{R}}_1, y_1), ({\overline{R}}_2, y_2), \ldots ,({\overline{R}}_u, y_u)\} \end{aligned}$$
(11)

where each tuple \(({\overline{R}}_u, y_u)\) represents the u-th sample of the labeled training dataset. Here, \({\overline{R}}_u \in \{({\overline{R}}_T, {\overline{R}}_F)_1, \ldots ({\overline{R}}_T, {\overline{R}}_F)_u\}\). The label \({y_u \in \{0,1\}}\) indicates the binary state: \(y_u = 0\) for the noise-only state \({H_0}\), and \(y_u = 1\) for the signal-present state \(H_1\). SS can thus be framed as a binary classification problem, and \(y_u\) is encoded as a one-hot vector to reflect this:

$$y_u = \left\{ \begin{aligned} & [1, 0],\quad H_0\\ & [0, 1], \quad H_1 \end{aligned}\right.$$
(12)

The labeled data \({\mathcal {D}}\) are then fed into the TFCFN for training. The output of the network is a probability vector normalized by the softmax function:

$$\begin{aligned} f_\theta ({\overline{R}}_u) = [f_{\theta |H_0}({\overline{R}}_u), f_{\theta |H_1}({\overline{R}}_u)] \end{aligned}$$
(13)

with

$$\begin{aligned} \sum _{i=0}^{1} f_{\theta |H_i}({\overline{R}}_u) = 1 \end{aligned}$$
(14)

here, \({\theta }\) represents the set of parameters of the TFCFN, and \({f_\theta ({\overline{R}}_u)}\) is the vector of probabilities, with \({f_{\theta |H_i}({\overline{R}}_u)}\) denoting the probability that the given sample \({\overline{R}}_u\) is classified as state \(H_i\).

To obtain the optimal parameter \({\theta }\), we accomplished this by minimizing the cross-entropy loss function using an Adam optimizer with a learning rate of 0.0005. The cross-entropy function is defined as follows:

$$\begin{aligned} {\mathcal {L}}(\theta ; {\overline{R}}_u, y_u) = y_u \log (f_{\theta |H_1}({\overline{R}}_u)) + (1 - y_u) \log (1 - f_{\theta |H_0}({\overline{R}}_u)) \end{aligned}$$
(15)

After obtaining a model with optimal parameters by training on the dataset \({{\mathcal {D}}}\), the determination of the PU state can be performed using the new test data. Typically, the result is taken from the category corresponding to the maximum probability in \({f_{\theta }({\overline{R}}_u)}\), which is denoted as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} H_0, & f_{\theta |H_0}(R_u) > f_{\theta |H_1}(R_u) \\ H_1, & f_{\theta |H_0}(R_u) < f_{\theta |H_1}(R_u) \end{array}\right. } \end{aligned}$$
(16)

In order to compare the experimental results more accurately, we are keeping a constant \(P_f\) for comparison. The method is to replace the judgment condition of Eq. (16) by a decision threshold \({\gamma }\)61. Concretely, a new dataset \({{\mathcal {D}}_\text {noise}}\) is created by randomly selecting purely noisy samples from dataset \({{\mathcal {D}}}\), where \({{\mathcal {D}}_\text {noise}} = \{({\overline{R}}'_1, 0), ({\overline{R}}'_2, 0),...,({\overline{R}}'_n, 0)\}\). Subsequently, this dataset is subjected to predictions using the trained model, and the probabilities of \(H_1\) states are subsequently ranked:

$$\begin{aligned} f_{\theta |H_1}({\overline{R}}'_a) \le f_{\theta |H_1}({\overline{R}}'_b),\, {\forall }\,1 \le a \le b \le n \end{aligned}$$
(17)

Finally, the decision threshold \({\gamma }\) can be represented as:

$$\begin{aligned} \gamma = f_{\theta |H_1}({\overline{R}}'_{round((1-P_f)n)}) \end{aligned}$$
(18)

where \({round(\cdot )}\) is rounding function. After obtaining \({\gamma }\), Eq. (16) transforms to the following judgment condition:

$$\begin{aligned} {\left\{ \begin{array}{ll} H_0, & f_{\theta |H_1}({\overline{R}}_u) < \gamma \\ H_1, & f_{\theta |H_1}({\overline{R}}_u) > \gamma \end{array}\right. } \end{aligned}$$
(19)

Performance evaluation

In this section, we first demonstrate the effectiveness of the cross-attention mechanism in TFCFN through ablation experiments. Next, we will evaluate the performance of TFCFN under constant \(P_f\) and different noise conditions, and compare it with existing SS techniques. At the same time, we will demonstrate the receiver operating characteristic (ROC) curves of TFCFN under different noise tail levels. Subsequently, the results of a series of generalization and robustness experiments will be analyzed. Finally, we will analyze and discuss the complexity of the model.

Ablation experiment

In the ablation experiment, we replace the cross-attention module, denoted as “CA”, with several common feature fusion methods to validate the effectiveness of the module. These methods include “Concat”, “Add”, and “Multiply”. The results are presented in Table 2, where accuracy, a commonly used metric in classification tasks, is employed as the performance indicator to intuitively compare the classification performance under different shape parameters of the GGD. In the experiments, the aforementioned modules and the “CA” were validated using only the X feature, while “CA + skip connection” incorporated the \(X_d\) feature for validation. All results are averaged over multiple runs.

Table 2 The ablation experiment results of TFCFN.
Full size table

Through the “Concat” operation, features \(X_t\) and \(X_f\) are concatenated in the channel dimension, which increases the number of features. However, experimental results indicate that this fusion strategy is not ideal in overall performance, despite maintaining a moderate level of parameter count and floating-point operations (FLOPs). When using the “Add” operation, the corresponding elements of features \(X_t\) and \(X_f\) are directly added to enhance the information content of the features. When the \(\beta =0.5\), there is a significant improvement in the performance of the model. The “Multiply” operation emphasizes the interaction between \(X_t\) and \(X_f\) features through element level multiplication, and shows good performance at \(\beta =1.5\). Similar to the “Add” operation, the “Multiply” operation also maintains the original dimensions of the features, so their parameter count and FLOPs are relatively low. The “CA” dynamically adjusts the importance of features by calculating the attention score between \(X_t\) and \(X_f\). This mechanism not only considers the interactions between features, but also establishes more complex dependency relationships between different features. The experimental results show that the “CA” performs the best in handling different noise shape parameters. Although its parameter count and FLOPs have increased, this is due to the additional computation required within the attention mechanism. In addition, when we introduce skip connection and add the most primitive feature information into the model, the performance is further improved.

Comparative experiment

In our experiments, we compare the proposed TFCFN model with existing deep learning-based methods and traditional method, which include ED32, DetectNet21, WT-ResNet24, ConvLSTM25, 1D-CNN26, 2D-CNN27, and MASSnet-B33. For a fair comparison, all schemes use the same original dataset and are fine-tuned to obtain optimal hyperparameters. The properties of these methods are presented in the Table 3.

Table 3 Properties of comparison methods.
Full size table

Figure 3 illustrates the \(P_d\) of all schemes at different SNRs when the \(P_f\) is constant at 0.1. Although the threshold calculation of the ED is derived from the GGD, its performance is lower than that of deep learning based methods. As shown in Fig. 3a, the characteristics of GGD noise approximate Gaussian noise when \(\beta =2\). ConvLSTM, WT-ResNet and DetectNet are schemes designed as SS algorithm in a Gaussian white noise environment. Observations show that the performance of TFCFN is similar to that of ConvLSTM when the SNR is below -14 dB. However, when the SNR exceeds -14 dB, TFCFN significantly outperforms the other schemes, and its \(P_d\) improves by about 7.5% compared to ConvLSTM. As the \(\beta\) decreases, the tail of the noise distribution thickens, indicating an increase in the probability of extreme values in the noise. This change has the most significant impact on traditional ED algorithm, whose performance is extremely dependent on accurate estimates of noise energy levels. The CNN and ConvLSTM show similar detection performance when the \(\beta\) is reduced to 1.5. At SNR below -16 dB, the performance of the schemes does not differ much. However, when the SNR is higher than -16dB, the performance of TFCFN is significantly improved compared to CNN and ConvLSTM, with an increase in \(P_d\) ranging from about 5% to 10%. In Fig. 3c, TFCFN outperforms the other schemes in terms of \(P_d\) at all SNRs, and only slightly underperforms in the -20 dB SNR condition. Compared with ConvLSTM, TFCFN improves the \(P_d\) by about 4% to 9%. In particular, TFCFN shows optimal performance at \(\beta =0.5\). Under the condition of -20 dB SNR, the \(P_d\) of TFCFN reaches 57%, which is significantly higher than other schemes by more than 40%. In addition, when the SNR is increased to above -16 dB, the \(P_d\) of TFCFN is more than 90%. From the analysis of the results, it can be seen that the method with GRU or LSTM structures performs better, indicating that long-term dependencies in the time domain play a significant role. On this basis, introducing frequency domain features further improves the \(P_d\). The performance differences between various methods can be more clearly understood through accuracy indicators, as shown in the Table 4.

Fig. 3
figure 3

Probability of detection of different methods at \(P_f = 0.1\)

Full size image
Table 4 Accuracy results of comparative experiments.
Full size table
Fig. 4
figure 4

ROC curves of different noise distribution at SNR = -18 dB.

Full size image

Figure 4 illustrates the curves of the \(P_d\) as a function of the \(P_f\), where different curves correspond to different GGD noise \(\beta\) values. In this figure, the curve shifts to the left overall as the \(\beta\) value decreases. This trend indicates that when the tail of the noise distribution becomes thicker, i.e., the \(\beta\) value decreases, the TFCFN is able to achieve a higher \(P_d\) while maintaining a low \(P_f\). In the TFCFN, the cross-attention mechanism allows the model to dynamically learn the importance of time-frequency features, which means that the model can automatically assign higher weights to features that are more informative in thick-tailed noise environments. At the same time, the stacking of multiple layers of convolution and recurrent structures increases the expressive power of the model, allowing it to capture more complex signal features. Taken together, the results show that TFCFN has higher \(P_d\) and better adaptability when dealing with non-Gaussian noise, especially noise distributions with thicker tails.

Generalization experiments

The impact of modulation methods

In this experiment, we study the classification of untrained signals with new modulation types by various methods. All models are trained using QPSK signals under the conditions of \(\beta=2\) and \(\beta =1\), respectively. Subsequently, BPSK and 16QAM signals were tested. The experimental results are shown in the Fig. 5, and all results maintain the \(P_f=0.1\). The experimental results revealed that when faced with new BPSK signals, the performance of 1D-CNN, 2D-CNN, WT-ResNet, and DetectNet all showed significant degradation. Compared with the results shown in Fig. 3, the \(P_d\) of TFCFN changes less and still maintains the best performance among all comparison methods. This discovery confirms that a fully trained TFCFN model can effectively detect new signals that have not been encountered before.

Fig. 5
figure 5

Performance of detecting new signals at \(P_f = 0.1\)

Full size image

The impact of noise uncertainty

Fig. 6
figure 6

Performance results under noise uncertainty at \(P_f = 0.1\)

Full size image

In real-world SS scenarios, the uncertainty of noise manifests as fluctuations in noise power over time, which may lead to significant performance degradation of certain detectors. In this experiment, the background noise is GGD noise. According to Eq. (2), when the shape parameter \(\beta\) remains fixed, \(\frac{\Gamma (3/\beta )}{\Gamma (1/\beta )}\) becomes a constant. Therefore, in the GGN model, only the parameter \(\alpha\) has an impact on the variance of noise, and its uncertainty can be represented by \(\alpha ^2\in [\frac{1}{\rho }\alpha _0^2, \rho \alpha _0^2]\), where \(\alpha _0^2\) is the nominal \(\alpha ^2\) and \(\rho\) is the uncertainty factor32. In Fig. 6, we use NU to represent uncertainty, and its transformation relationship with \(\rho = 10^{\frac{NU}{10}}\), with NU expressed in dB52. In the experiment, all methods used the trained model shown in Fig. 3, and it can be considered that \(NU=0dB\). We conduct tests on the cases of \(\beta =2\) and \(\beta =1\) respectively to evaluate the changes in model performance at \(NU=0.2 \, {\rm dB}\) and \(NU=0.5\, {\rm dB}\). The experimental results indicate that ED is most affected as it requires a higher estimation of noise power. On the contrary, the results of TFCFN remained stable and were not significantly affected. This indicates that TFCFN has reliability in environments with noise uncertainty.

The impact of shape parameter on GGD

In this section, we aim to estimate the generalization ability of the trained model under different shape parameter conditions of GGD. Specifically, we use the model trained in a GGD noise environment with \(\beta =1.5\) to test its performance on unknown datasets generated under different shape parameters \(\beta =2\) and \(\beta =1\). As shown in Fig. 7a, after training under the condition of \(\beta =1.5\), the performance of the TFCFN model on the test data of \(\beta =2\) is quite similar to that of the model trained and tested directly under the condition of \(\beta =2\) (see Fig. 3a). This indicates that the TFCFN has good robustness in handling the transition from slightly sharp shapes to smoother Gaussian distribution, and can effectively generalize to distributions similar to the training data. However, as shown in Fig. 7b, when the TFCFN is evaluated on the test dataset with \(\beta =1\), its performance decreased compared to the results shown in Fig. 3c. This is because the noise at \(\beta =1\) has sharper peaks and heavier tails, and the model failed to fully capture the specific characteristics of these noises during training. However, the TFCFN still exhibits certain functionality, and its \(P_d\) is still prominent among the compared models.

Fig. 7
figure 7

Generalization experiment results of shape parameter \(\beta\)

Full size image

Comparison experiment of other noise distributions

To verify the robustness of TFCFN to other noise distributions, we conduct experiments on GMM noise and \(S\alpha S\) noise. The performance comparison and analysis under each noise distribution will be introduced below.

The PDF of a GMM is composed of a weighted sum of PDF of a set of Gaussian distributions. The PDF of a binary GMM is as follows:

$$\begin{aligned} f(x) = \frac{1 - \epsilon }{\sqrt{2\pi \sigma _1^2}}exp(-\frac{x^2}{2\sigma _1^2}) + \frac{\epsilon }{\sqrt{2\pi \sigma _2^2}}exp(-\frac{x^2}{2\sigma _2^2}) \end{aligned}$$
(20)

where \(\epsilon\) is a mixed parameter, and \(0< \epsilon < 1\). In general, when the variance of the noise satisfies \(\sigma _2^2>> \sigma _1^2\) and \(\epsilon<< 1\), the variance of Gaussian noise \(\sigma _2^2\) is used to describe sudden pulses or interferences with short duration and large amplitude changes. At the same time, the Gaussian distribution with variance of \(\sigma _1^2\) dominates in the background noise. The total noise variance \(\sigma ^2\) is \((1 - \epsilon )\sigma _1^2 + \epsilon \sigma _2^2\). In the experiment, set \(\sigma _1^2 = 1\), \(\sigma _2^2 = 4\), \(\epsilon = 0.5\), and \(P_f=0.1\) to observe the perceptual performance of all models on the GMM5. As shown in Fig. 8, under multiple SNR conditions, the TFCFN model exhibits significantly better detection performance than other models. Specifically, under SNR = -8 dB, the \(P_d\) of TFCFN exceeds 90%. In the SNR range of -16 dB to -8 dB, TFCFN has an \(P_d\) increase of about 5% compared to the other models. The experimental results show that TFCFN can still achieve ideal detection performance under GMM.

Fig. 8
figure 8

Performance results under GMM noise environments.

Full size image

The PDF of \(\alpha\)-stable distribution does not have a closed expression, so it is defined through the characteristic function:

$$\begin{aligned} \phi (z) = exp\{j\mu z - \gamma |z|^\alpha [1+j\beta sign(z)\omega (z, \alpha )]\} \end{aligned}$$
(21)

where \(\alpha (0 < \alpha \le 2)\) denotes the characteristic exponent, \(\beta (-1 \le \beta \le 1)\) represents symmetrical parameter, \(\gamma\) is the proportional parameter, \(\mu\) is the positional parameter, sign(z) is a sign function, and \(\omega (z, \alpha )\) is define as:

$$\begin{aligned} \omega (z, \alpha ) = {\left\{ \begin{array}{ll} tan(\frac{\pi \alpha }{2}), & \alpha \ne 1 \\ \frac{2}{\pi }log|z|, & \alpha = 1 \end{array}\right. } \end{aligned}$$
(22)

When \(\beta =0\), the \(\alpha\)-stable distribution is symmetric about \(\mu\) and degenerates into a \(S\alpha S\) distribution. Specifically, when \(\alpha =2\), the \(S\alpha S\) distribution transforms into a Gaussian distribution; When \(\alpha =1\), it degenerates into a Cauchy distribution62. In the experiment, we mainly focus on the performance of TFCFN under the conditions of \(\alpha =1.5\) and \(\alpha =1.2\)27. In addition, other related parameters were set as follows: \(\beta =0\), \(\mu =0\), \(\gamma =1\), \(P_f=0.1\). Since the \(S\alpha S\) distribution does not possess a finite second-order moments, its variance becomes undefined. Therefore, in scenarios with additive \(S\alpha S\) noise, the generalized signal-to-noise ratio (GSNR) is commonly used as a measurement metric. The definition of GSNR is as follows:

$$\begin{aligned} GSNR = 10log_{10}(\frac{\sigma _s^2}{\gamma }) \end{aligned}$$
(23)

where \(\sigma _s^2\) represents the variance of the signal. Figure 9a shows the detection performance of each model under different GSNR condition when the \(\alpha =1.5\). Overall, the TFCFN performs better than other models. In the range of GSNR from -20 dB to -14dB, the \(P_d\) of the TFCFN is quite similar to other models. However, within the range of GSNR from -12 dB to -6 dB, the \(P_d\) of the TFCFN is about 10% higher than other models. As shown in Figure 9b, when the \(\alpha\) value is adjusted to 1.2, the pulse characteristics of the noise become more prominent. Within the GSNR range of -16 dB to -8 dB, the results are higher than those obtained when \(\alpha =1.5\), while still maintaining a higher level than other models.

Fig. 9
figure 9

Performance results under \(S\alpha S\) noise environments.

Full size image

Complexity analysis

In deep learning, the number of parameters and the FLOPs are common metrics used to measure the complexity of a model, which can be regarded as the space complexity and time complexity, respectively. In Table 5, we present in detail the computational complexity analysis based on deep learning methods, where l and \(D_l\) represent the index and number of layers of the network layer, respectively. In a Conv1D, \(u_l\), \(k_l\), and \(m_l\) represent the number of channels in the l-th layer, the size of the convolution kernel, and the length of the output sequence, respectively. In LSTM and GRU, \(e_l\) and \(h_l\) represent the size of the embedding layer and the number of hidden units in the l-th layer, respectively. In addition, \(d_l\) represents the number of neurons in the l-th dense layer52. Compared to Conv1D, the convolutional kernels and feature maps in Conv2D are two-dimensional. Therefore, we use \(m_l^h \times m_l^w\) to represent the size of the output feature map, and \(k_l^h \times k_l^w\) to denote the size of the convolutional kernel. ConvLSTM replaces fully connected layers with convolutional layers internally, thereby changing the computational cost of convolution. Compared to LSTM, GRU reduces the number of parameters and FLOPs of the model by reducing the computation of on gating structure. In addition, during the classification stage, we adopted a global pooling layer to reduce data dimensionality, thereby reducing the number of input neurons in the Dense layer, further reducing the overall parameter and computational complexity. Please refer to the Table 5 for specific comparative data. It can be seen that the TFCFN has much fewer parameters than other comparative models, while its FLOPs remain at a slightly lower to moderate level. The actual FLOPs are influenced by the size of features and the number of channels. In both 2D-CNN and MASSnet, pooling operations are used to reduce the size of features, resulting in a decrease in computational complexity. However, their characteristic information may be lost.

Table 5 The complexity of all models.
Full size table

Conclusion

In this paper, we studied a multi feature fusion network called TFCFN. This network effectively integrates time-domain and frequency-domain features through cross-attention mechanism, which can better adapt to Gaussian noise and strong impulse noise environments simulated by GGD. The experimental results show that TFCFN performs better than the comparative methods under various shape parameters of GGD, while maintaining lower complexity. In addition, the experiment verified that the network has robustness under new modulation methods, noise models (GMM and \(S \alpha S\)), and noise uncertainty. However, we are still dissatisfied with the results at extremely low SNR, and TFCFN has certain limitations in multi antenna scenarios. Future work will further optimize TFCFN to improve its performance and practicality in practical communication systems.