Introduction

Distributed optical fiber sensor is an emerging seismic exploration technology1, which was first applied in the field of seismic exploration, and then gradually extended to vertical seismic profiling(VSP)2. The DAS system is based on the photoelastic effect of optical fiber, and the seismic wave monitoring is realized by detecting the phase, wavelength, and other parameters of the optical signal stimulated by the artificial seismic source3. The data is converted into recognizable geological information after a series of operations such as denoising, inversion, and reconstruction. Compared with traditional seismic exploration methods, DAS has many advantages, such as low cost, high sensitivity, strong electromagnetic interference resistance, and convenient layout4. However, the background noise energy is often stronger than the effective signal in the seismic data received by DAS. In addition, the ringing noise and optical instrument noise caused by the poor coupling between the cable and the receiving surface during laying, which are unique to DAS records, also leads to the low signal-to-noise ratio of DAS seismic data5. Therefore, how to attenuate the complex noise in DAS records, recover the effective signal, and improve the SNR of the records has become one of the hottest issues in the field of exploration data processing.

To solve the seismic data denoising problems, the researchers have proposed a variety of different methods: First is the filtering method, which mainly includes band-pass filtering(BPF)6,7, time-frequency peak filtering (TFPF)8, median filtering9,10, Wiener filtering11, and so on. This kind of method achieves denoising by selecting and retaining the frequency band corresponding to the effective signal, but the selection of key parameters of filtering needs to balance between noise suppression and signal retention, the removal of low-frequency noise may lead to the loss of low-frequency effective signal. The second type is based on mode decomposition. Different modes contain different frequency components, and the denoising of seismic exploration data is achieved by retaining the modes that contain effective signals. This kind of method may cause mode aliasing during the process of seismic records with severe overlap between the effective signal spectrum and the noise spectrum. The typical methods include empirical mode decomposition(EMD)12, ensemble empirical mode decomposition13, and variational mode decomposition14. The third type is based on sparse transformations, such as wavelet transform(WT)15,16, shearlet transform17, and curvelet transform18. In this method, the domain of seismic data is changed, then the threshold function is set to distinguish the effective signal from the noise, and finally, the denoising of the record is realized by inverse transformation according to the frequency domain coefficient corresponding to the effective signal. As the parameter setting strategy lacks generalization, the denoised seismic record cannot completely retain the effective signal components and contains obvious noise residue when processing complex seismic data. The fourth kind of method is based on low-rank matrix approximation, which mainly includes principal component analysis19 and robust principal component analysis20. This method takes advantage of the similarity between the theoretical pure seismic record and the low-rank structure to downrank the noisy data to separate the signal from the noise. However, downgrading will cause the loss of original seismic data information, resulting in poor denoising results. Other representative methods, such as F-X deconvolution21, singular value decomposition22,23, and dictionary learning24, have been applied to solve seismic exploration problems and have shown certain denoising ability, but the denoising result of complex background noise in the real DAS record is not good enough.

With the continuous improvement of computer computing ability, and the continuous improvement of artificial intelligence theory25, convolutional neural networks and other deep learning-based methods have become a research hotspot. Because of its excellent performance in computer vision tasks such as semantic segmentation and target recognition. CNN has also been applied in many fields of seismic exploration, such as inversion, waveform classification, and first arrival pickup26. Classical deep learning architectures have also been applied to noise suppression of seismic exploration data, such as feedforward denoising neural networks (DnCNN)27, FFD-Net20, U-Net28,29, and residual network30,31. Novel noise reduction frameworks based on CNN such as DeepSeg also shows excellent denoising ability, which is efficient in learning sparse representation of the data and adaptively capturing seismic signals corrupted with noise32. The parameters of the CNN-based denoising network are optimized for every epoch of the training process to establish a mapping between noisy data and clean signals and make sure that the output of the network is close to the label data. These deep learning methods provide a more accurate and clear recovery of effective signals from the data. However, since the structural framework of classical networks is simple, it lacks multiscale information interaction and the fusion of information at different depths, which limits the ability of the network to extract latent features from complex seismic data.

To attenuate the background noise and recover the effective signals in DAS records, a multiscale sparse asymmetric attention convolutional neural network is proposed in this paper. About the network structure, a sparse block(SB) is designed at the beginning of the network to preprocess the data and extract the shallow features in the data. Dilated convolutional layers are inserted between ordinary convolutional layers to expand the receptive field without consuming additional computing resources, and improve the network denoising performance. The shallow features obtained after preprocessing are used as the input of asymmetric block (AB) for deeper feature extraction. AB uses convolution instead of pooling to complete the downsampling operation, extracts features in the feature maps of different scales, and then restores all the feature maps to the original size through deconvolution, and then integrates them as the input of the next block. The pyramid attention block (PAB) focuses on the target information in the local features by assigning different weights, and at the same time suppresses the useless information, which further improves the denoising performance of the network.

The major contributions are outlined as follows.

1) For effectively attenuating the intense DAS background noise, a denoising network using multiscale strategy is proposed.

2) To ensure the denoising performance, a high-quality and comprehensive training dataset, combining synthetic data and field noise data, is built and apply to train the network.

3) Both synthetic and field data are processed to evaluate the performance of the trained models, and also compared with some popular methods, including conventional and CNN-based algorithms.

The experimental results show that the MSAACNN proposed in this paper can recover the signal from DAS records with strong background noise.

Network architecture

Architecture of MSAACNN

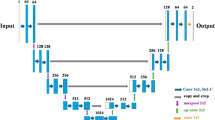
The overall structure of the proposed network consists of three blocks: SB, AB, and PAB, as shown in Fig. 1. SB consists of convolutional layers (Conv), dilated convolutional layers, and rectifier linear units (Relu). AB takes the asymmetric module composed of dilated convolution and asymmetric convolution as the basic unit and performs feature extraction and scale transformation on the inputs of two resolutions. PAB is composed of Conv at different scales, Relu, residual structure, sigmoid function, and multiplier. The feature extraction of the network is realized by convolution between the convolution kernel and the input matrix, and the feature matrix will continue to perform convolution operation with the convolution kernel in the next Conv as input, to realize the transition from low-dimensional features to high-dimensional features.

Fig. 1
figure 1

Architecture of the MSAACNN. (a) Network architecture. (b) Asymmetric unit. (c) Pyramid attention block.

Full size image

1) Sparse block: The research shows that sparsity is effective for image applications33, which can improve the network denoising performance and training efficiency, and reduce the depth of the network, network computing cost, and memory consumption. The part that is activated is called a high-energy point, and based on the principle that there are fewer high-energy points and more low-energy points, and high-energy points should be unevenly distributed, we propose a sparse module for noise suppression in seismic data. Because the dilated convolution itself shows sparsity and has a larger receptive field than the ordinary convolution, it can map more contextual information, so the dilated convolution can be regarded as a high-energy point in the SB. As shown in Fig. 1(a), SB is composed of eight convolutional layers, and we set the dilated convolution with an expansion factor of 2 in the 4th, 6th, and 8th layers of the network, and after the preliminary feature extraction, the features of different depths in the block are selected for fusion and used as the output of SB.

2) Asymmetric block: As the backbone of the network, AB consists of multiple asymmetric units as shown in Fig. 1(b). 1 × 1 Conv reduces the number of channels, making the structure of the entire network more flexible and reducing the amount of computation. In each unit, a 1 × 3 convolution kernel, a 3 × 1 convolution kernel, and a 3 × 3 convolution kernel with expansion factor 3 are used for feature extraction and fusion. Although dilated convolution has a larger receptive field, it also causes the loss of feature information. The asymmetric convolution not only improves the ability of the network to extract asymmetric features but also complements the dilated convolution to obtain more complete feature information. To reduce the computational cost, multiscale network structures usually downsample the feature map many times, but the test results show that the model with too many downsampling operations can not recover the weak signal in the seismic exploration data. Therefore, there is no continuous downsampling structure designed in AB. The feature resolution is alternately transformed between 64 × 64 and 32 × 32 in AB, and the feature information of the same depth and different scales is always interactive. The residual structure of the asymmetric unit and the fusion of all the native resolution features at the end of the module can avoid the problem of shallow information loss caused by the increase in the depth of the network.

3) Pyramid attention block: The structure of the PAB is shown in Fig. 1(c), the number of channels is reduced by 1 × 1 Conv, and then the resolution of the feature map is reduced by downsampling to expand the receptive field. The resolution is reduced from 64 × 64 to 32 × 32, and the original resolution of the feature map is restored by upsampling. In PAB, convolutional kernels of 3 × 3, 5 × 5, and 7 × 7 are deployed to extract features from different size receptive fields to capture global information better. Skip connection is applied to avoid the loss of information caused by the increase in depth, and 1 × 1 Conv recovers the number of channels. The sigmoid function makes the output range from 0 to 1 and inputs the output as a weight to the multiplier together with the input of PAB. The feature matrix after feature enhancement then goes through three 3 × 3 Conv + Relu to reconstruct and finally obtains the output of PAB, that is, the final denoising result.

Denoising theory

The input of MSAACNN is the noisy seismic data y, it can be thought of as a linear summation of a clean signal x with random noise n as shown in the equation:

$$y=x+n$$
(1)

By training the convolutional neural network structure proposed in this paper, the mapping relationship between the DAS record and the estimated signal can be established, as shown in the formula:

$$\widehat {x}=R(y,\theta )$$
(2)

where R represents the mapping relationship, \(\widehat {x}\) represents the estimated signals, and θ represents the network parameters. In the training process, the network uses the loss function to continuously optimize the parameters to make the estimated signals close to the theoretical pure signals, and the expression of the loss function is shown as follows:

$$l(\theta )=\frac{1}{{2B}}{\left\| {R({y_i},\theta ) - {x_i}} \right\|^2}$$
(3)

where B stands for the batch size, \({x_i}\) and \({y_i}\) denotes the labeled data and the noise training data patches, and \(\left\| {} \right\|\) is the Frobenius norm, which is used in the loss function. By minimizing the value of the loss function, we can obtain the optimal parameter set \({\theta _{opt}}\), and the final denoising result is denoted as:

$${\widehat {x}_{opt}}=R({y_i},{\theta _{opt}})$$
(4)

Network training

Construction of training datasets

CNN is a highly data-driven deep learning method, and the quantity and quality of data are important factors affecting network performance, so building a high-quality and comprehensive training dataset is an important aspect of the training process. In this paper, synthetic data and field data are used to construct a training dataset for training seismic denoising models.

In the process of training, the noisy record is required as the network input, and the corresponding clean signal is the desired output. However, due to the complex signal interference in seismic exploration, it is impossible to obtain a pure reflected signal from the field DAS record. Therefore, this paper uses the forward modeling method to simulate the pure signals in the DAS data, and at the same time, the rationality of the synthetic data is ensured by analyzing the field seismic profile records collected in advance. The elastic wave equation is used to simulate the wave field information, and the forward modeling records for constructing the training set are obtained after exciting the seismic wavelets of different frequencies. The detailed parameters are shown in Table 1. Figure 2(a) shows the forward modeling stratigraphic velocity model, with the black vertical line on the left showing the location of the receivers and the red triangle in the upper right corner indicating the location of the artificial seismic source. Figure 2(b) shows the synthetic DAS seismic record obtained from the forward modeling velocity model. Based on constructing a velocity model with 200 different parameter settings, the corresponding theoretical pure DAS records were calculated by using the acoustic wave equation and the finite difference method. 20,096 signal chips were intercepted by using the sliding window of 64 × 64. The quality of the noise dataset will also affect the final training results of the network, and it is expected that the network can suppress specific noise, so the noise dataset should contain such noise, so the noise in the field exploration record of DAS without source is selected to construct the noise set. After the interception, 20,000 noise patches of 64 × 64 were obtained, and the noise training set was obtained after normalization. Figure 3 shows the sample of signal and noise patches in the training set. To train a robust model, we randomly pair the signal patches with the noise patches during the training process. The noise energy is scaled and superimposed with the signal patch to obtain a noisy data patch, and the SNR is in the range of [–10,0] dB, which is used for network training together with the signal patches.

Table 1 Physical parameters for the forward models (DAS data).
Full size table
Fig. 2
figure 2

Forward models and synthetic records.

Full size image
Fig. 3
figure 3

Typical patches for signal and noise training data. (a) Signal patches. (b) Noise patches.

Full size image

Experimental environment and training process

The software platform used in this paper is Matlab2021b, the matconvnet toolkit is used to realize the network training, and the NVIDIA GeForce RTX 3060 GPU, AMD Ryzen 7 4800 H with Radeon Graphics CPU and 16 GB RAM are used to form the hardware experimental environment. The Adam optimization algorithm was used for network training, the learning rate was set to [10–4, 10–5, 10–6] which changes every 20 epochs, the batch normalized size was set to 64, and the training patch size was set to 64 × 64. To facilitate training, the training data was normalized and the training epoch was 60. After 60 training epochs, the loss function has stabilized, and the model with the best performance is selected to process the synthetic data and field DAS seismic exploration records. The training parameters for the MSAACNN are listed in Table 2.

Table 2 Network parameters.
Full size table

Processing of modeling data and quantitative comparison

To verify the effectiveness of the trained models, we process one of the records contained in the training dataset. Moreover, the corresponding results are shown in Fig. 4, and promising results are observed, indicating their denoising capability. For the denoising results of different methods, we used the SNR and Root-Mean-Square Error (RMSE) to quantitatively compare. The SNR reflects the noise suppression capability of the method, while the RMSE reflects the signal retention capability of the method. The expressions for SNR and RMSE are as follows:

Fig. 4
figure 4

Validation results of the modeling data. (a) Original modeling data. (b) Denoising result. (c) Filtered noise.

Full size image
$$\:SNR=10{{log}}_{10}\left(\frac{{\sum\:}_{i=1}^{M}{\sum\:}_{j=1}^{N}{\widehat{x}}_{opt}(i,j{)}^{2}}{{\sum\:}_{i=1}^{M}{\sum\:}_{j=1}^{N}{\left(x(i,j)-{\widehat{x}}_{opt}(i,j)\right)}^{2}}\right)$$
(5)
$$\:RMSE=\sqrt{\frac{1}{MN}{\sum\:}_{i=1}^{M}{\sum\:}_{j=1}^{N}{\left(x(i,j)-{\widehat{x}}_{opt}(i,j)\right)}^{2}}$$
(6)

where x represents the clean signal, \(\:{\widehat{x}}_{opt}\) represents the denoised result, and M and N represent the number of traces and samples, respectively.

Processing of synthetic record

The denoising performance of the MSAACNN network was verified by processing the synthetic noisy DAS records. Firstly, forward modeling is used to construct a synthetic noise record, with a trace space of 1 m and a sampling frequency of 2500 Hz, as shown in Fig. 5(a). Figure 5(b) shows the noise data used to synthesize the synthetic noise record, including various types of noise, for example, horizontal and time-varying noise, and so on. Figure 5(c) shows a synthetic record with an SNR of − 5 dB. It is obvious that due to the interference of strong background noise, the reflected signal is badly polluted, and the deep weak reflection signal is difficult to identify (marked by the red arrow).

Fig. 5
figure 5

Processed noisy synthetic record. (a) Clean synthetic data. (b) Added field noise record. (c) Noisy record.

Full size image

Competing methods

To accurately testify the denoising performance of the MSAACNN network, WT, BPF, EEMD, and DnCNN were selected as comparison methods to denoise the synthetic record (Fig. 5(c)) and then analyze the performance qualitatively and quantitatively. The WT basis function is db4 wavelet, and the number of decomposition layers is 15, using the soft thresholding. The BPF band-pass frequency range is set to [3–42 Hz] to retain the effective signal. The EEMD method selects the 3rd, 4th, and 5th intrinsic mode functions for superposition. DnCNN is a 20-layer network structure, which is trained using the same experimental environment and dataset as MSAACNN.

Comparison of the denoising results

The denoising of the synthetic record using the above method and the MSAACNN proposed in this paper is shown in Fig. 6. Figure 6(a) shows the synthetic record and noise, and Fig. 6(b) shows the WT method, which cannot accurately recover the effective signal, and only suppresses part of the high-frequency noise with obvious signal components in the noise record. Figure 6(c) shows the BPF method, which recovers the effective signal to a certain extent, but there is still interference with co-channel noise and distortion of the recovered signal in the denoised record. Figure 6(d) shows the EEMD method, which recovers a more pronounced effective signal, but there is still horizontal noise that cannot be removed in the denoised result. The above three traditional methods have a certain denoising ability, but only for certain specific noise types, and there are types of noise that cannot be effectively handled. In contrast, the denoising results of DnCNN (Fig. 6(e)) and MSAACNN (Fig. 6(f)) are superior, and the filtered noise is closer to the actual noise. However, there is obvious background noise in the record, which is processed by DnCNN, and the filtered noise also contains effective signal components, resulting in the attenuation of the signal amplitude in the denoised record, and the weak signal cannot be completely recovered. However, in the results of MSAACNN processing, the continuity of the lineups is better, the weak signal is recovered, and there is no obvious noise residue in the denoised result.

Fig. 6
figure 6

Comparison between the denoising results obtained by different methods. (a) Clean synthetic data and added noise record. (b)–(f) Attenuation results obtained by WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image

On this basis, the area in the yellow box in Fig. 6 is zoomed in and compared, as shown in Fig. 7. As shown in Fig. 7(a), the optical noise in the noisy record heavily contaminates the reflected lineups. The experimental results show that the WT method (Fig. 7(b)) cannot suppress the interference of strong noise, and the BPF (Fig. 7(c)) can recover the lineup to a certain extent, but there is distortion and obvious noise residue, EEMD (Fig. 7(d)) is slightly better than the BPF method but the suppression of background noise is not ideal, and although DnCNN (Fig. 7(e)) can effectively suppress noise, the recovery of low-energy signal is incomplete. The MSAACNN proposed in this paper (Fig. 7(f)) is significantly better than the other four methods in terms of the continuity and clarity of effective signal recovery. The results above verify the effectiveness of MSAACNN in recovering the signal components in synthetic seismic records under the influence of strong background noise.

Fig. 7
figure 7

Comparison for the area of interest (marked by the yellow block in Fig. 7). (a) Synthetic data before processing. (b)–(f) Enlarged results of WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image

Moreover, the frequency domain analysis of the denoised records and filtered noise is carried out, and the F-K spectral results are shown in Fig. 8. Figure 8(a) shows the clean signal and the field DAS background noise, and the signal components and noise components are significantly aliased in the frequency domain. As shown in Fig. 8(b) and Fig. 8(c), the WT and BPF methods cannot effectively remove the aliasing noise component, the noise filtered out by WT contains signal components, and BPF cannot suppress the noise in the band-pass range. The signal components in the EEMD method (Fig. 8(d)) are distorted. Both DnCNN (Fig. 8(e)) and MSAACNN (Fig. 8(f)) can effectively suppress noise, but there is obvious noise residue in the results of DnCNN, and the result of MSAACNN is closest to the pure signal, which further verifies the effectiveness of MSAACNN. More comprehensive, accurate, and reliable results can be obtained by processing the noisy records of different SNRs, and the differences between the ability of different methods to improve SNR and RMSE are compared, as shown in Table 3. After observation and analysis, it can be seen that MSAACNN has obvious advantages over other methods in improving SNR and RMSE, and the SNR of records with different SNR is increased by more than 18 dB, indicating that MSAACNN is effective in synthetic seismic data denoising.

Fig. 8
figure 8

Spectral domain analysis. (a) F-K spectrum for a clean signal and added noise data. (b)–(f) F-K spectra for WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image
Table 3 Comparison of SNR and RMSE for different attenuation methods.
Full size table

In summary, it can be concluded that MSAACNN can recover weakly reflected signals while suppressing complex noise in DAS seismic records, and its denoising ability has obvious advantages.

Processing of field record

The field DAS-VSP seismic records were denoised, and the results are shown in Fig. 9. Figure 9(a) shows the original DAS-VSP record, consisting of 1372 traces at a sampling frequency of 2500 Hz. The noise components in the field record are very complex, such as the attenuation noise, horizontal noise, time-varying optical noise, and coupling noise identified by the red arrow, which seriously affects the identification of effective signals in the record. In the same way as the synthetic records, the field DAS seismic records are processed and compared using the WT, BPF, EEMD, DnCNN, and MSAACNN methods. The parameters of the WT, BPF, and EEMD methods were selected following those used to process the synthetic record. Since it was not possible to construct a signal training set using actual records, DnCNN and MSAACNN used an optimal synthetic record processing model to process the field records.

Fig. 9
figure 9

Denoising results of different methods for the field data. (a) Field DAS data. (b)–(f) Results of WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image

The experimental results show that the WT method (Fig. 9(b)) has no obvious suppression effect on the strong background noise in the field DAS record and cannot recover the effective information in the record. The BPF method (Fig. 9(c)) can recover the effective signal, but the record contains residual noise, and the signal is over-smoothing. The result of the EEMD method (Fig. 9(d)) has significant residual horizontal noise. Similar to the denoising results of synthetic records, the noise suppression effect of DnCNN (Fig. 9(e)) and MSAACNN (Fig. 9(f)) for field DAS records is better than that of traditional methods, and there are still problems of incomplete noise suppression and signal amplitude attenuation in the record processed by DnCNN. In contrast, MSAACNN can accurately recover the effective signal components covered by complex noise, and there is no obvious noise residue in the processed record. On this basis, the green box area in Fig. 9 is enlarged and compared, and the results are shown in Fig. 10. Figure 10(a) shows the field DAS record, where there is significant time-varying optical noise in this region, and the reflected signal is difficult to identify. From the results, it can be seen that the WT method (Fig. 10(b)) has almost no suppression effect on the noise in this area, and the target signal is still difficult to identify due to noise interference. The signal in the seismic record processed by the BPF method (Fig. 10(c)) is disturbed by the noise of the same frequency, and the signal is broadened. The EEMD method (Fig. 10(d)) has a certain recovery effect on the signal, but due to the influence of background noise, the detailed texture of the signal is hardly restored. The overall noise suppression of DnCNN (Fig. 10(e)) is fine, but the suppression of optical noise is poor, the record contains obvious noise residues and the lineups are not fully recovered. MSAACNN (Fig. 10(f)) has a more obvious suppression effect on the complex background noise in the field DAS record than other methods and can recover continuous, clear, and complete lineups, and there is no obvious noise residue in the recovered record. In summary, MSAACNN has good noise suppression ability for field DAS seismic exploration records with complex noise types and low SNR, which verifies that the proposed network has more advantages in denoising performance and effective signal retention ability and meets the practical needs of DAS-VSP data processing.

Fig. 10
figure 10

Enlargement results for the green box area in Fig. 9. (a) Field DAS data. (b)–(f) Attenuation results of WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image

In order to fully demonstrate the effectiveness of the proposed method, we use the same model to denoise another field record, and the results are shown in Figs. 11 and 12. The experimental results show that the proposed method has a good suppression effect on the different kinds of noise indicated by the red arrow in Fig. 11(a), and can retain the effective signal components to the greatest extent.

Fig. 11
figure 11

Denoising results of different methods for another field data. (a) Field DAS data. (b)–(f) Results of WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image
Fig. 12
figure 12

Enlargement results for the green box area in Fig. 11. (a) Field DAS data. (b)–(f) Attenuation results of WT, BPF, EEMD, DnCNN, and MSAACNN, respectively.

Full size image

Conclusion

To solve the problem of low data SNR caused by complex noise types and serious influence on effective signals in DAS seismic exploration records, this paper proposes a multiscale convolutional neural network MSAACNN based on sparsity, asymmetric convolution, and attention mechanism to process field DAS records. MSAACNN preprocesses the shallow information of the input features through the sparse block, uses the dilated convolution with different expansion factors to enlarge the receptive field, and maps more context information. Then, the interaction between multiscale feature information is realized through the asymmetric block, which is helpful for the network to extract asymmetric features, and residual structure is adopted to strengthen the connection between shallow information and deep information to avoid information loss. Finally, the pyramid attention block focuses on the local features and suppresses the redundant information to enhance the feature information learned by the whole network and improve the denoising ability of the model. To prove the effectiveness of MSAACNN, the synthetic seismic records and field DAS records were processed using traditional methods and classical deep learning network framework, and the processing results were compared with those of MSAACNN. Experimental results show that MSAACNN has a significant effect on the suppression of background noise in DAS records, can retain continuous and complete reflection information, and improves the SNR of seismic records. In summary, MSAACNN can meet the needs of DAS seismic exploration record processing and provide a certain reference for the design and optimization of a noise suppression network.