Introduction

In the field of thermal engineering and fluid dynamics, the attempt of advanced heat-transmitting solutions has led to the growth of hybrid nanofluids, an innovative class of engineered fluids. These fluids, which incorporate nanoparticles into traditional heat transfer mediums, have garnered significant interest due to their potential to enhance heat transfer efficiency. Notably, magnetic oxide (Fe3O4) and multi-walled carbon nanotubes (MWCNTs) have emerged as prominent additives, each contributing unique thermal and structural properties. Hybrid nanofluids represent a cutting-edge approach to thermal management, offering improved thermal conductivity, stability, and other desirable traits compared to conventional heat transfer fluids. By dispersing Fe3O4 and MWCNTs within a base fluid (water), these nanofluids present a versatile solution for various industrial and technological applications. Many studies have been performed to explore the dynamics of nanofluids, with a focus on understanding the complex behaviours of hybrid nanofluids under various external conditions. The first claim about nanofluids was made by Choi et al.1 which improved heat transfer rates compared with unpolluted fluids. He began working at Argonne National Laboratory in 1995. Derikvand et al.2 inspected forced convection and entropy formation of a non-Newtonian nanofluid containing ethylene glycol and MWCNTs-Fe3O4 in a microchannel with convex surfaces. Cicek et al.3 discovered the influence of movement and deposition of MWCNTs-Fe3O4 within a square enclosure under the flow of a hybrid nanofluid driven by natural convection and this study likely delved into the presence of these nanoparticles affects their movement and deposition patterns within the enclosure as a result of buoyancy-driven fluid flow. The result of the MHD thermo-magnetic convection concert of a Fe3O4/Water ferrofluid stream in a special dimpled tube was examined experimentally by Gursoy et al.4.

The challenges of efficient heat transmission become particularly pronounced in complex environments characterized by stratified media, where fluid layers with distinct properties coexist. Conventional heat transfer fluids often struggle to navigate these conditions effectively. The integration of Fe3O4 and MWCNTs into the fluid matrix holds promise for overcoming these challenges and enhancing heat transfer efficiency within stratified media. Alharbi et al.5 discovered the result of hall current in the hybrid squeezing nanofluid stream between binary rotating disks in a thermally stratified medium. Jamrus et al.6 addressed thermally stratified ternary hybrid nanofluid flowing in a mixed convective manner transversely a stretching/shrinking sheet: the outcome of magnetohydrodynamics and velocity slip. Heat and mass transmission and three-dimensional boundary layer flow via hybrid nanofluid stagnation point flow was considered by Ferdows et al.7.

Furthermore, the interaction between hybrid nanofluids and external factors such as radiation and magnetohydrodynamics (MHD) introduces additional complexities. Radiation heat transfer mechanisms and MHD effects can significantly influence the behaviour of nanofluids, particularly in stratified environments. Understanding and optimizing the interplay between these factors is crucial for harnessing the full potential of hybrid nanofluids in thermal systems. Fe3O4 nanoparticles, renowned for their magnetic properties, and MWCNTs, valued for their high aspect ratio and thermal conductivity, offer complementary advantages when dispersed in fluid matrices. Hosseinzadeh et al.8 analysed optimization of emission and convection heat transport using magnetic field study of a hybrid nanofluid in a wavy permeable field. Lutera et al.9 studied mathematical solution for an unstable nanofluid stream with magnetic, endothermic reaction, viscous dissipation, and solid volume fraction effects on an exponentially moving vertical plate. Waqas et al.10 addressed numerical modelling of heat transmission and hybrid nanofluid stream across parallel surfaces incorporating suction/injection and magnetic effect. A finite difference approach to MHD Casson ternary hybrid nanofluid flow over a vertical plate with heat radiation was investigated by Sakkaravarthi et al.11. Hayat et al.12 studied numerical investigation of heat transmission and thin film flow of Fe3O4 and Al2O3 nanoparticles distributed in water across a vertical stretched sheet. Fractional analysis of unsteady radiative brinkman-type nanofluid flow consisting of CoFe2O3 nanoparticles across a vertical plate was addressed by Bilal et al.13. Abderrahmane et al.14 addressed thermal behaviour under magnetic fields of three-dimensional Darcy-Forchheimer permeable rectangular wavy enclosures holding a Fe3O4/H2O ferro-nanofluid. Shao et al.15 studied drug delivery systems using a statistical method to optimize the heat transmit rate for the Au/Fe3O4-blood nanofluid stream using entropy investigation. Yahaya et al.16 exposed dual solutions of unstable mixed convection hybrid nanofluid stream through a vertical Riga plate with radiation outcome. Goud et al.17 examined thermostatically stratified magnetic fluid flow through an accelerated vertical porous plate with an impact on viscous dissipation is affected by thermal radiation. Zainuddin et al.18 investigated computational resolution of electro magnetohydrodynamic GO-Fe3O4/water stream and temperature transmission above Shifting Riga Plate through effects of thermal energy and heat absorption/generation. Jakeer et al.19 analysed a nonlinear study of radiation-effect Darcy-Forchheimer stream in MHD ternary hybrid nanofluid (Cu-CNT-Ti/H2O). The outcome of heat source/sink and thermal emission on an unstable MHD squeezing Darcy-Forchheimer stream of Fe3O4 Casson nanofluid was exposed by Waheed et al.20. Mathematical simulations of heat conservation in hybrid nanofluids with chemical reactions, viscous dissipation, and inclination was investigated by Manigandan et al.21. Chu et al.22 addressed model-based study compares unstable hybrid nanofluid stream between two parallel plates with particle shape properties using magnetohydrodynamics.

Rajesh et al.23 analysed the effect of a moving/exponentially accelerated upright plate on unstable stream and heat transmission in hybrid nanofluids. Khan et al.24 explored numerical investigation of unstable hybrid nanofluid flow containing water, ferrous oxide, and carbon nanotubes under varying magnetic fields. Kumar et al.25 inspected the natural convective nanofluid stream over an impulsively starting upright plate and its impact on MHD heat transfer due to thermal radiation. Haribabu26 investigated an unstable magnetic Casson fluid stream across an infinite vertical permeable plate accompanied by a chemical reaction. Madhu et al.27 considered the outcome of activation energy and quadratic thermal radiation on an oblique stagnation point hybrid nanofluid stream over a cylinder. Madhukesh et al.28 addressed the influences of quadratic thermal radiation and waste discharge concentration on time-dependent nanofluid flow over a porous rotating sphere. Vinutha et al.29 investigated sensitivity analysis and RSM optimization in a magnetic field ternary nanofluid stream with quadratic radiation and activation energy among parallel plates. Li, Shuguan et al.30 considered the aspects of using an induced MHD to drive a ferromagnetic hybrid nanofluid flow that transfers heat and mass in response to pollutant concentration. Aggregation of nanoparticles and the process of thermophoretic element deposition in the stream of micropolar nanofluid across a stretched sheet were discovered by Yu et al.31. Ramesh et al.32 investigated magnetized nanoliquid thermal transfer across a lubricated surface with heat source and sink and activation energy. Analysis of warmth transmission in a three-dimensional unstable magnetic fluid stream of ternary hybrid nanofluid based on water transporting three different-shaped nanoparticles: A comparative investigation was inspected by Kumar et al.33. Gamaoun et al.34 discovered the impact of thermal radiation and fluctuating nanofluid thickness on heat transmission over a stretching sheet using the Keller Box method in the presence of MHD. These comprehensive investigations collectively contribute to a deeper perception of the performance of hybrid nanofluids in various conditions, providing valuable insights for further advancements in nanofluid dynamics and heat transmission applications.

The novelty of this work lies in its comprehensive examination of the combined outcomes of magnetohydrodynamics and radiation along with stratified medium on energy transfer dynamics over a vertical plate using a hybrid nanofluid composed of Fe3O4 nanoparticles and MWCNTs diffused in water. While existing studies often focus on individual factors or simpler fluid compositions, our research uniquely integrates these complex influences into a single analysis. This holistic approach offers a more realistic representation of real-world scenarios and provides valuable insights into the synergistic interactions between different phenomena. Accordingly, the mathematical investigation of a hybrid nanofluid stream across a vertical plate is our most modern study endeavour. The consequences of the current examination are displayed in tables and graphs for the velocity, temperature and concentration outlines. Addressing the following questions is the main goal and novel aspect of this research.

  • How does the stratified medium influence the velocity and temperature outline?

  • How is the temperature contour affected by significant values of radiation parameter?

  • What are the variations observed in all the three outlines for change in the values of solid volume fraction?

  • What are the belongings on the concentration outline when the Schmidt number attains large values?

  • How will the magnetic parameter, radiation and solid fraction impact engineering factors?

Mathematical modelling

To examine the dynamics of unstable, incompressible, electrically conducting and viscous hybrid nanofluid flow in the occurrence of an external MHD, we use conservative partial differential equations.

To idealize the model, several assumptions are made.

  • Fluid properties are considered constant until thickness changes occur, the external MHD is supposed to be consistent throughout domain, and the dissipation of ohmic energy is deemed negligible.

  • Additionally, the effects of plate velocity and radiation heat flux on heat flow are considered insignificant.

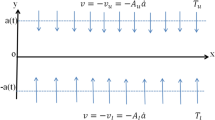
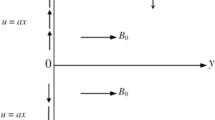
Establishing the organize system (x, y) is set up, the plate y-axis is vertical and the x-axis is located on the plate, as exposed in Fig. 1. Originally, both the plate and the hybrid nanofluid remain stationary, with the ambient temperature prevailing throughout the system. The fluid consists of water-based magnetic nanoparticles such as Fe3O4 and MWCNTs. The surrounding fluid’s temperature is assumed to remain at the ambient level throughout the process. The governing equations considered for this analysis include those for natural convection flow, continuity, momentum, and energy, enabling a comprehensive examination of the fluid dynamics and heat transfer phenomena involved. The thermophysical properties of hybrid nanofluids associated with Fe3O4 and MWCNTs with base fluid water are outlined in Tables 1 and 2. The subsequent governing equations are below by applying the Boussinesq approximation and the aforementioned hypotheses. Khan et al.24

Fig. 1
figure 1

The physical model of the formulation.

Full size image
Table 1 Thermal characteristics of water with nanoparticles: Khan et al.24.
Full size table
Table 2 The effective characteristics of hybrid nanofluids associated with Fe3O4 and MWCNTs are given below, Khan et al.24.
Full size table

Dimensional governing equations

$$\frac{\partial u}{{\partial x}} = 0\,$$
(1)

In unsteady-state situation, the momentum equation for a hybrid nanofluid on a vertical plate among the magnetohydrodynamic outcome accounts for time-varying fluid flow and evolving magnetic field interactions.

$$\frac{\partial u}{{\partial t^{*} }} = \nu_{h\,\,n\,f} \left[ {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right] - \frac{{\sigma_{h\,\,n\,f} }}{{\rho_{h\,n\,f} }}B_{0}^{2} u + \frac{{(\rho \beta )_{h\,\,n\,f} }}{{\rho_{h\,n\,f} }}g(T - T_{\infty } ) + \frac{{(\rho \beta^{\,*} )_{h\,\,n\,f} }}{{\rho_{h\,\,n\,f} }}g(C\, - C_{\infty } )\,$$
(2)

The energy equation for the unsteady-state stream of a hybrid nanofluid on a vertical plate through radiation and stratified media involves considerations of thermal conduction, convection, and radiation heat transmission. The equation accounts for the time-dependent variations in temperature distribution along the plate surface, influenced by the fluid’s nanoparticle concentration and radiation properties.

$$\frac{\partial T}{{\partial t^{*} }} = \frac{{k_{h\,n\,f} }}{{(\rho C_{p} )_{h\,n\,f} }}\left[ {\frac{{\partial^{2} T}}{{\partial y\,^{2} }}} \right] - \frac{1}{{(\rho C_{p} )_{h\,n\,f} }}\left( {\frac{{\partial q_{r} }}{\partial y}} \right) - \gamma u$$
(3)

This equation set is essential for understanding the dynamic behaviour of nanofluid flow in applications such as mass transfer enhancement.

$$\frac{\partial C}{{\partial t^{*} }} = D_{m} \left[ {\frac{{\partial^{2} C}}{{\partial y^{2} }}} \right]\,$$
(4)

Dimensional boundary conditions

Kumar et al.25 are

$$\left. \begin{gathered} u = 0,\,\,\,T = T_{\infty } ,\,\,\,C = C_{\infty } \,at\,t \le 0\,for\,all\,\,y \ge 0 \hfill \\ u = 0,\,\,\,T = T_{w} ,\,\,\,C = C_{w} \,\,at\,\,t \ge 0\,for\,\,all\,y = 0 \hfill \\ u \to 0,\,\,T \to T_{\infty } ,\,\,C \to C_{\infty } \,\,at\,\,t \ge 0\,\,for\,all\,\,y \to \infty \hfill \\ \end{gathered} \right\}$$
(5)

Non dimensional quantities

Non-dimensional quantities play a crucial function in characterizing behaviour of hybrid nanofluids on vertical plate flow with magnetic field, and radiation effects in unsteady state conditions. Parameters such as the Grashof and Nusselt number are scaled to eliminate dependence on system-specific properties, enabling comparison and analysis across different experimental setups and theoretical models. Kumar et al.25

$$\left. \begin{gathered} U = \frac{u}{{U_{0} }},\,\,Y = \frac{{U_{0} y}}{{\nu_{f} }},\,\,t = \frac{{U_{0}^{2} t^{*} }}{{\nu_{f} }},\,\,\phi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\,\,\theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},Gc = \frac{{g\beta_{f}^{*} (C_{w} - C_{\infty } )\nu_{f} }}{{U_{0} U_{0}^{2} }}\,,\, \hfill \\ \,Gr = \frac{{g\beta_{f} (T_{w} - T_{\infty } )\nu_{f} }}{{U_{0} U_{0}^{2} }}\,,\Pr = \frac{{\nu_{f} }}{{\alpha_{f} }}\,,Rd = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{k\,k^{*} }}\,,\,\,Sc = \frac{{\nu_{f} }}{{D_{m} }},M^{2} = \frac{{\sigma_{f} \,B_{0}^{2} \,\nu_{f} }}{{\rho_{f} \,U_{0}^{2} }}\,,\,\,\, \hfill \\ \,S = \frac{\gamma }{{U_{0} \left( {T_{w} - T_{\infty } } \right)}} \hfill \\ \end{gathered} \right\}$$
(6)

The radiative heat flux \(q_{r}{^\prime}\) is determined by utilizing the Roseland approximation,

$$q_{r}{^\prime} = - \frac{{4\sigma^{*} }}{{3kk^{*} }}\,\frac{{\partial T^{4} }}{\partial y}\,$$
(7)

The Taylors series expansion of T4 about T∞ is

$$T^{4} = T_{\infty }^{4} + 4\left[ {T - T_{\infty } \,\,} \right]T_{\infty }^{3} + 6\left[ {T - T_{\infty } } \right]^{2} T_{\infty }^{2} + ...........\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$
$$T^{4} = 4T_{\infty }^{3} T - 3T_{\infty }^{4}$$
(8)

Then Eq. (7) and (8) substitute in Eq. (3) reduces to,

$$\frac{\partial T}{{\partial t^{*} }} = \,\frac{{k_{h\,n\,f} }}{{(\rho C_{p} )_{h\,n\,f} }}\left( {\frac{{\partial^{2} T}}{{\partial y\,^{2} }}} \right) + \frac{{16\,\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} (\rho C_{p} )_{h\,n\,f} }}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - \gamma u$$
(9)

Dimensionless governing equations

The following governing equations are dimensionless,

$$\frac{\partial U}{{\partial X}} = 0\,\,$$
(10)

The non-dimensional momentum equations for the unsteady state stream of a hybrid nanofluid on a vertical plate among the magnetic outcome describe fluid motion in terms of dimensionless parameters. These equations incorporate the outcomes of magnetic field, unsteadiness, and nanoparticle suspension.

$$\frac{\partial U}{{\partial t}} = \frac{{\rho_{f} }}{{\rho_{hnf} }}\frac{{\mu_{h\,\,n\,f} }}{{\mu_{\,f} }}\left[ {\frac{{\partial^{2} U}}{{\partial Y{}^{2}}}} \right] - \frac{{\frac{{\sigma_{h\,\,n\,f} }}{{\rho_{h\,n\,f} }}}}{{\frac{{\sigma_{\,f} }}{{\rho_{f} }}}}M^{2} U + \frac{{(\rho \beta )_{h\,\,n\,f} }}{{\rho_{h\,n\,f} \beta_{\,f} }}Gr\theta + \frac{{(\rho \beta )_{h\,\,n\,f} }}{{\rho_{h\,n\,f} \beta_{\,f} }}Gc\phi \,$$
(11)

The non-dimensional energy equations for unsteady state stream of a hybrid nanofluid on a vertical plate among radiation outcome typically involve dimensionless parameters such as Prandtl number, thermal conductivity ratio, and stratified medium. These equations express the balance of energy in terms of non-dimensional temperature gradients, aiding in analyzing heat transfer characteristics.

$$\frac{\partial \theta }{{\partial t}} = \frac{{\frac{{k_{h\,n\,f} }}{{(\rho C_{p} )_{h\,n\,f} }}}}{{\frac{{k_{\,f} }}{{(\rho C_{p} )_{\,f} }}}}\frac{1}{\Pr }\left( {1 + \frac{{k_{f} }}{{k_{hnf} }}\frac{4}{3}Rd} \right)\left[ {\frac{{\partial^{2} \theta }}{{\partial Y{}^{2}}}} \right] + S\,U$$
(12)

Non-dimensional mass equations for the unsteady-state stream of a hybrid nanofluid on a vertical plate involve dimensionless parameter Schmidt number. These equations govern the transport of mass within the fluid, considering the influence of nanoparticles.

$$\frac{\partial \phi }{{\partial t}} = \frac{{D_{hnf} }}{{D_{f} }}\frac{1}{Sc}\left[ {\frac{{\partial^{2} \phi }}{{\partial Y^{2} }}} \right]\,$$
(13)

Dimensionless boundary conditions

$$\,\left. \begin{gathered} U = 0,\,\,\,\theta = \,\,1,\,\,\phi = \,\,1\,,\,\,at\,y = 0,\,\,for\,all\,t > 0 \hfill \\ U = 0,\,\,\,\theta = \,\,0,\,\,\phi = \,\,0\,,\,at\,y = \infty ,\,\,for\,all\,t > 0 \hfill \\ \end{gathered} \right\}$$
(14)

Engineering interest

Skin-friction coefficient \(\left( {C_{f} } \right)\), Nusselt \(\left( {Nu} \right)\) and Sherwood numbers \(\left( {Sh} \right)\) are key physical quantities related to the characteristics of double diffusive during transport, are shown below. Kumar et al.26

$$C_{f} = \,\frac{1}{{(1 - \phi )^{2.5} }}\left( {\frac{\partial U}{{\partial Y}}} \right)_{Y = \,0} \,,\,\,\,Nu = - \frac{{k_{h\,n\,f} }}{{k_{b\,f} }}\left( {\frac{\partial \theta }{{\partial Y}}} \right)_{Y\, = \,0} ,\,\,\,\,\,Sh = - \left( {\frac{\partial \phi }{{\partial y}}} \right)_{y\, = \,0}$$

Method of solution

Flow chart

The thermal characteristics of Fe3O4–MWCNTs/ H2O nanoparticles are used to solve coupled non-linear differential Eqs. (11), (12), and (13) as well as limit conditions (14) using the explicit finite difference technique of the DuFort-Frankel method, which is numerically implemented in MATLAB. Haribabu26.

$$\begin{gathered} \left( {\frac{{U_{i,\,j + 1} - U_{i,\,j - 1} }}{2\Delta t}} \right)\, = A_{1} \left( {\frac{{U_{i - 1,\,j} - U_{i,\,j + 1} - U_{i,\,j - 1} + U_{i + 1,\,j} }}{{\left( {\Delta Y} \right)^{2} }}} \right) - A_{2} \left( {\frac{1}{2}M\,\left( {U_{i,\,j + 1} - U_{i,\,j - 1} } \right)} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + A_{3} \left( {\frac{1}{2}\,Gr\,\left( {\theta_{i,\,j + 1} - \theta_{i,\,j - 1} } \right)} \right)\, + A_{4} \left( {\frac{1}{2}\,Gr\,\left( {\phi_{i,\,j + 1} - \phi_{i,\,j - 1} } \right)} \right) \hfill \\ \end{gathered}$$
(15)
$$\left( {\frac{{\theta_{i,\,j + 1} - \theta_{i,\,j - 1} }}{2\Delta t}} \right)\, = \frac{{B_{1} }}{\Pr }\,\left( {1 + \frac{4}{3}Rd} \right)\,\left( {\frac{{\theta_{i - 1,\,j} - \theta_{i,\,j + 1} - \theta_{i,\,j - 1} + \theta_{i + 1,\,j} }}{{\left( {\Delta Y} \right)^{2} }}} \right)\, + \left( {\frac{1}{2}S\left( {U_{i,\,j + 1} - U_{i,\,j - 1} } \right)} \right)\,\,$$
(16)
$$\left( {\frac{{\phi_{i,\,j + 1} - \phi_{i,\,j - 1} }}{2\Delta t}} \right)\, = \frac{1}{Sc}\,\,\left( {\frac{{\phi_{i - 1,\,j} - \phi_{i,\,j + 1} - \phi_{i,\,j - 1} + \phi_{i + 1,\,j} }}{{\left( {\Delta Y} \right)^{2} }}} \right)\,$$
(17)

Initial and boundary conditions take the following forms

$$U_{i,0} = 0,\,\,\,\theta_{i,0} = \,\,1,\,\,\phi_{i,0} = \,\,1\,,\,\,\,\,for\,all\,\,\,i$$
(18)
$$U_{0,j} = 0,\,\,\,\theta_{0,j} = \,\,1,\,\,\phi_{0,j} = \,\,1\,,\,\,\,\,\,for\,all\,j = 1,\,2,....$$
(19)
$$U_{\infty ,j} \to 0,\,\,\theta_{\infty ,j} \to 0,\,\phi_{\infty ,j} \to 0\,for\,all\,j = 1,\,2,....$$
(20)

Here the suffix \(^{\prime}i^{\prime}\) corresponds to \(Y\) and \(^{\prime}j\,\,^{\prime}\) corresponds to \(t\) .

Also \(\Delta t = t_{j + 1} - t_{j}\) and \(\Delta Y = Y_{j + 1} - Y_{j}\).

For computational purposes, the problem’s physical domain is measured as a finite, constrained rectangle with finite dimensions. Mesh sizes, while running a range of \(\Delta\) y = 0.001, 0.002, and 0.009 with no important dissimilarity in the numerical values of velocity, temperature, and concentration, outline coding for a mathematical system as defined. As a result, in order to maintain consistency all through the computation, the mesh size \(\Delta\) y = 0.001 was chosen. These approximations involve expressing the derivative of a function in terms of its values at neighbouring grid points. Moreover, Finite difference method is computationally efficient, especially for problems with regular grid can require a significant number of computational resources, particularly for problems with fine grid or high-dimensional systems. To check and verify validate the accuracy of overall mathematical algorithm, a contrasting the numerical outcomes using two approaches bvp4c and Finite difference method (FDM) for Skin friction with varying values of M. With earlier published works of Khan et al.24 as exposed in Table 3. The range of the parameters are taken from the standard literature as M = 0–3,Gc = 2–8, Gr = 2–5, Rd = 0–3, S = 0–0.5, Sc = 2–8.

Table 3 Comparison and validation of the mathematical results by two methods bvp4c and FDM for skin friction (Cf) for varying the values of M.
Full size table

Model validation

For the sake of correctness of the present work, see Table 3 which provides a comparison and validation of the mathematical results by two methods bvp4c and FDM.

Result and discussion

The unsteady flow of hybrid nanofluid over a vertical plate among combined outcomes of magnetohydrodynamics, radiation along with the presence of Fe3O4 nanoparticles and MWCNTs, the finite difference method is commonly employed for numerical solution. In this computational approach, the governing equations, which typically include the Navier-Stokes equations for fluid flow, heat equation accounting for radiation, Maxwell’s equations for MHD are discretized using finite difference approximations. The properties of the hybrid nanofluid, including those of Fe3O4 nanoparticles and MWCNTs, are incorporated into the mathematical model through appropriate boundary conditions and material properties such as thermal conductivity, viscosity, and magnetic susceptibility.The finite difference method allows for the simulation of complex fluid stream phenomena and the interaction between various physical effects such as heat transfer, fluid dynamics, magnetic field. Figure 1 shows the physical model of the problem whereas in Figure 2 the flow chart for the proposed model is provided.

Fig. 2
figure 2

Flow chart for the proposed model.

Full size image

Narrative for graph

Velocity profile

Figure 3 depicts the velocity profile as influenced by increasing Radiation (\(Rd\)) intensity. This increase in radiation can alter the thermal boundary level close to the plate surface, impacting the fluid’s behaviour. As radiation intensity rises, the thermal gradient across the fluid boundary layer increases, thereby influencing its viscosity and density. Consequently, the velocity profile near the plate experiences modifications, exhibiting changes such as increased flow velocities, altered boundary layer thickness, or enhanced fluid mixing due to convective currents induced by temperature gradients. The physical mechanisms underlying this phenomenon are multifaceted. Enhanced radiation intensities can lead to higher energy absorption by the fluid, resultant in augmented fluid temperature expansion, which in turn, affect its density and viscosity. The Fe₃O₄ nanoparticles enhance thermal conductivity and improve the fluid’s magnetic responsiveness, which increases energy absorption and subsequently raises the temperature of the fluid. MWCNTs contribute to improved heat distribution due to their high aspect ratio and excellent thermal conductivity, which enhances the overall convective heat transfer. This synergy leads to reduced thermal resistance and a more pronounced velocity profile compared to other nanofluids, which do not combine both magnetic and thermal conductivity benefits.

Fig. 3
figure 3

Velocity profile for increasing value of Radiation (\(Rd\)).

Full size image

Figure 4 depicts the velocity profile as influenced by increasing Magnetic field (\(M\)) intensity. This increase in magnetic field can alter the velocity boundary level close to the plate surface, impacting fluid’s behaviour. Understanding the physical mechanisms behind the observed velocity profile changes due to varying magnetic field values is crucial. As magnetic field surges, the Lorentz force becomes more prominent, altering the fluid flow behaviour. In the case of water with Fe3O4 nanoparticles and MWCNTs, the Lorentz force, influenced by \(M\), interacts with the fluid motion. This interaction affects the velocity distribution close to the plate surface. Physically, the occurrence of Fe3O4 nanoparticles and MWCNTs contributes to changes in fluid properties, such as thickness and thermal conductivity, moving momentum and energy transport within the flow. The Fe3O4 nanoparticles increase the fluid’s magnetic responsiveness, enhancing momentum transfer in the occurrence of MHD, while MWCNTs improve heat distribution due to their high conductivity. This combination results in a more effective reduction of thermal resistance, allowing for a higher velocity profile and better heat transfer than nanofluids containing only Fe3O4 ₄ or MWCNTs alone.

Fig. 4
figure 4

Velocity profile for increasing value of Magnetic field (\(M\)).

Full size image

As depicted in Fig. 5, the velocity profile reveals intriguing trends with increasing thermal Grashof number (\(G\,r\)). This phenomenon can be elucidated by considering the interplay of buoyancy forces induced by thermal gradients, fluid viscosity, and nanoparticle dispersion effects. With a rising Grashof number, buoyancy-driven flow intensifies, promoting fluid motion away from the heated plate. The presence of Fe3O4 nanoparticles and MWCNTs further modulates this behaviour, as their respective properties influence thermal conductivity and viscosity, thereby altering the velocity distribution across the boundary layer. Fe3O4 contributes to higher thermal conductivity and magnetic response, while MWCNTs improve heat distribution due to their structural properties. Together, these effects amplify buoyancy-driven convection, resulting in a more pronounced velocity profile. This combined action enhances heat transfer rates more effectively than other nanofluids, which lack the dual advantages provided by both Fe3O4 and MWCNTs.

Fig. 5
figure 5

Velocity profile for increasing value of thermal Grashof number (\(G\,r\)).

Full size image

The velocity contour depicted in Fig. 6, illustrate the variation of velocity concerning the increasing mass Grashof number (\(Gc\)), a parameter characterizing buoyancy-driven flows. In this context, as the mass Grashof number rises, indicating higher buoyancy forces relative to viscous forces, the velocity profile exhibits a discernible augmentation. This augmentation can be elucidated through the physical mechanisms underlying the interaction between the flow dynamics and the constituents involved namely water, Fe3O4 nanoparticles, and MWCNTs. The presence of Fe3O4 nanoparticles and MWCNTs within the water base of the nanofluid alters its thermophysical properties, affecting its convective heat transfer characteristics. Fe3O4 nanoparticles exhibit ferromagnetic properties which, below the control of external magnetic field can induce additional flow effects, further influencing the velocity distribution along the vertical plate. As the Gc increases, buoyancy forces become more dominant, leading to enhanced fluid motion and convective energy transmit. This results in a more pronounced velocity profile. The contact between the buoyancy-driven flow, magnetic effects, and the thermophysical property of the nanofluid components collectively contribute to observed variation in velocity with increasing mass Grashof number.

Fig. 6
figure 6

Velocity profile for increasing value of mass Grashof number (\(Gc\)).

Full size image

In Fig. 7, it is illustrated the outcome of increasing the value of the stratified medium (\(S\)) on the velocity profile. A noticeable amplification tendency is seen in the velocity outline as this parameter increases. Examining context of fluid flow in a stratified media can help us better understand the physical process underlying this phenomenon. Density gradients cause alterations in the behaviour of fluids passing through such a medium, which is composed of layers of differing densities. Changes in the velocity profile are caused by these gradients, which also cause changes in the fluid’s velocity distribution. An increasing value of the stratified media parameter indicates a more marked difference in characteristics between the various levels of the media. The contact of density gradients on fluid flow is amplified by this increase in heterogeneity. As an outcome, the fluid’s velocity profile noticeably improves as it passes through these more diverse layers. The process that is responsible for this increase is the combination of momentum transfer and buoyancy forces in the stratified medium. Furthermore, changes in the stratified medium characteristic modify the extent to which these buoyancy effects mark the dynamics of the stream, which in turn affects the velocity profile. In conclusion, the increased impact of density gradients on fluid flow behaviour inside the heterogeneous medium might explain the observed rise in the velocity outline with a growing value of the stratified media. This knowledge emphasizes how buoyancy forces and momentum transfer interact intricately to shape velocity distributions in settings with stratified layers.

Fig. 7
figure 7

Velocity profile for increasing value of Stratified media (\(S\)).

Full size image

Temperature profile

In Fig. 8, it is demonstrated the control of stratified media (\(S\)) on the temperature outline, showcasing a notable trend where in the profile ascends with raises in the value of the stratified media. This phenomenon is indicative of the significant role that stratified media plays in altering temperature distribution within a given system. The physical mechanism underlying this observation can be attributed to the interaction between the properties of the media and the heat transmits occurring within it. Stratified media, characterized by variations in composition, density, or other relevant parameters across different layers, introduces complexities into heat transmission phenomena. As the value of the stratified media parameter rises, it signifies a greater degree of stratification within the media. This heightened stratification leads to alterations in temperature distribution due to several factors. With increased stratification, variations in density and thermal conductivity between layers create temperature gradients that drive convective flow patterns. These currents influence the transfer of heat throughout the medium, impacting the temperature profile. Furthermore, the stratified structure alters the propagation of thermal waves within the media. Variations in material properties between layers effect in modify in the speed and attenuation of thermal waves, affecting how temperature distributes over time and space. Consequently, an increase in the stratified media parameter amplifies these effects, leading to a noticeable shift in the temperature outline.

Fig. 8
figure 8

Temperature profile for increasing value of Stratified media (\(S\)).

Full size image

In Fig. 9, it is illustrated the temperature contour, showcasing the nuanced effect of increasing Radiation (\(Rd\)) intensity on the nanofluid system. As radiation levels escalate, the temperature profile exhibits a discernible rise, manifesting a direct correlation between radiation intensity and temperature elevation. This observation underscores the pivotal role of radiation in influencing the thermal behaviour of the hybrid nanofluid, comprising water, Fe3O4 nanoparticles, and MWCNTs. Fe3O4enhances the fluid’s response to radiation due to its magnetic properties, while MWCNTs efficiently spread the absorbed heat due to their high thermal conductivity. This dual mechanism allows the hybrid nanofluid to achieve superior heat transfer, making it more effective than the other nanofluids under the same conditions. Understanding such intricate temperature variations elucidates the intricate dynamics within these systems, facilitating optimized design and performance enhancement in various engineering applications.

Fig. 9
figure 9

Temperature contour for increasing the value of the Radiation (\(Rd\)).

Full size image

Concentration profile

In Fig. 10, it is depicted that the concentration profile for increasing Radiation (\(Rd\)) levels, the observed decrease in the profile reflects the augmented dispersion and mixing facilitated by intensified thermal convection induced by higher radiation intensities. This evolution culminates in reaching a steady-state concentration profile, where the influences of radiation, fluid dynamics, and particle dispersion reach a dynamic equilibrium. Initially, as radiation intensity rises, it enhances thermal energy transfer within the nanofluid. This augmented energy input triggers more vigorous fluid motion, leading to enhanced mixing and dispersion of Fe3O4 nanoparticles and MWCNTs within the fluid. As the concentration profile evolves, the increasing radiation intensity continues to drive more pronounced thermal convection and dispersion effects. Consequently, the concentration profile decreases, indicative of enhanced mixing and dispersion, until it ultimately reaches a steady state. At this steady state, the system achieves equilibrium, with the concentration profile stabilizing as the influence of radiation, fluid flow, and particle dispersion balances out.

Fig. 10
figure 10

Concentration profile for increasing value of the Radiation (\(Rd\)).

Full size image

Figure 11 displays, the concentration profile, which provides information about the hybrid nanofluid’s behaviour as the Schmidt number (\(Sc\)) increases. Initially, the profile exhibits a rising trend, indicating heightened mass transfer rates attributed to higher Schmidt numbers. This rise suggests enhanced diffusion of the solute species, facilitated by increased molecular diffusion relative to momentum diffusion. As the Schmidt number continues to escalate, the profile eventually reaches a steady-state condition. This equilibrium state signifies a balance between convective and diffusive transport mechanisms, wherein the rate of solute diffusion stabilizes, and concentration gradients become constant over time. The physical mechanism underlying this phenomenon involves intricate interplays between various factors. Elevated Schmidt numbers intensify the dominance of molecular diffusion over convective transport, leading to rapid solute dispersion. However, as the Schmidt number reaches a critical value, the diffusion process saturates, resulting in the establishment of a steady-state concentration profile. This equilibrium arises from the interplay between diffusion, convection, and chemical reaction kinetics within the nanofluid system. Particularly, the presence of Fe3O4 nanoparticles and MWCNTs further complicates the dynamics by influencing the fluid’s thermophysical properties, such viscosity and thermal conductivity, thereby altering mass transfer characteristics.

Fig. 11
figure 11

Concentration profile for increasing value of the Schmidt number (\(Sc\)).

Full size image

Table 4 examined the presented quantitate values are revealed that, the skin frictions are gradually increased by the key parameters \(Gc\),\(Gr\) and \(Rd\) while it is decreases with \(M\) and \(Sc\). Further, the heat transfer rate enhanced by \(S\),\(Gc\), and \(Gr\) while it is reducing with \(M\) and \(Rd\). In addition, the mass transfer rate is increases by the \(Sc\).

Table 4 Results of skin friction \(\left( {Cf} \right)\), Nusselt number \(\left( {Nu} \right)\) and Sherwood number \(\left( {Sh} \right)\) for increasing the different parameters values of \(M,\,Gc,\,Gr,Rd,\,\) and \(S.\).
Full size table

Conclusion

This study explores the complex dynamics hybrid nanofluid of heat transfer over a vertical plate under unsteady-state conditions, incorporating magnetic hydrodynamics and radiation effects along with the stratified medium. Using the explicit finite difference approach of the Dufort-Frankel method, convert the dimensional governing equations into non-dimensional forms for numerical analysis, which is employed numerically in MATLAB to assess the performance of water, magnetic oxide, and multi-wall carbon nanotubes as working fluids. Additionally, we visualize velocity, temperature and concentration profiles through plots to elucidate fluid behaviour. This study indicates that the quantitative result reveals that the temperature profile escalates among growing value of radiation. In contrast, the profiles of a velocity and concentration show a decrease as the values of magnetohydrodynamics increase.

The primary findings are summarized as follows:

  • Heightened radiation levels induce a proportional escalation in the temperature profile, indicating a direct correlation between radiation intensity and thermal distribution within the medium.

  • Higher values of magnetic field are associated with a discernible reduction in velocity profiles, suggesting that increased magnetic field parameters impede fluid flow, likely suitable to influence of magnetic field on the conductive properties of the medium.

  • Increasing the stratified media parameter leads to a rising temperature profile due to intensified convective currents and altered propagation of thermal waves within the medium.

Future work

The present problem is limited to examine the oblique stratified medium hybrid nanofluid flow on infinite vertical plate under the influence of quadratic, nonlinear and linear thermal radiation and magnetic field. Future research stemming from this study could explore additional parameters such as different fluid properties, plate geometries, or boundary conditions, validating numerical results through experimental measurements and comparisons with analytical solutions. Advanced modelling techniques like computational fluid dynamics (CFD) simulations could be employed to capture more complex phenomena, while optimization studies could determine optimal configurations for enhancing heat transfer efficiency. Further investigations into transient heat transfer phenomena, sensitivity analysis, and practical applications in heat exchangers, thermal management systems, or renewable energy technologies are warranted. Experimental validation, sensitivity analysis, and extension to three-dimensional systems could enhance the study’s applicability and accuracy, while exploration of novel materials and nanofluids could offer insights into potential advancements in heat transfer technologies.