Introduction

Slope risk management is an important issue in the construction and operation of geotechnical engineering1. Analytical and numerical simulation2,3 are effective analysis methods, but due to their abstraction, simplification and a series of basic assumptions on engineering information, the calculation results are difficult to completely and accurately reflect the actual situation of the project4,5,6. On the other hand, these methods require certain knowledge reserves and operating procedures, so it is difficult to realize real-time evaluation, analysis, and promotion on actual engineering sites7.

For the slope of the tunnel entrance section, the construction factors such as tunnel blasting excavation destroy the original stability of the slope, resulting in a potential landslide trend8. Rainfall and temperature changes will aggravate this trend, forming a hidden danger of instability and collapse of the tunnel entrance section9. Wang SH pointed out that the surface settlement of the tunnel portal section is characterized by 'complexity and nonlinear dynamic change characteristics’ under the interference of external factors10. Therefore, it is necessary to establish a time series prediction model. It can predict and warn the risk of large slope displacement based on the characteristics of slope displacement data at the tunnel entrance section11.

Time series prediction12 is considered to be an effective method for evaluating engineering risks based on slope displacement. However, the traditional time series model has the problems such as inaccurate manual measurement and unequal time interval of measurement data13. Researchers usually take interpolation14 and data denoising15 to solve this problem, and the internet of things (IoT) will also be a good solution16,17,18. On the other hand, the existing time series only consider the influence of historical data on the trend of displacement, and assumed that these historical data can reflect the geological characteristics of the slope, the degree of disturbance and other information. But for slopes that are obviously affected by specific factors, this is clearly not enough. Considering the natural environment of the Wendong tunnel on the Molin Expressway in Yunnan, China studied in this paper, it has been found in practice that the changes in rainfall and temperature differences during the construction of other tunnels in the same area have a significant impact on the slope stability of the tunnel entrance section. Therefore, in this study, these two factors are used as input parameters to establish an multivariate time series prediction model.

The traditional time series methods mainly include curve fitting method19, statistical analysis method20,21,22, gray system method23, etc. These methods are mainly suitable for describing simple displacement series with significant trends, which are difficult to meet the complex engineering requirements in tunnel entrance section. Intelligent algorithms based on machine learning24 have been gradually used in slope time series prediction in recent years, such as artificial neural networks25,26, support vector machines27, extreme learning machines28, and Gaussian processes29,30. In this process, biological optimization strategies are generally used to improve the parameter dependence of machine learning models, such as differential evolution31, particle swarm optimization32, and fish swarm algorithm33.

Considering that the number of samples collected in the time series prediction process of the tunnel entrance slope is very limited, this study chooses LSSVM to establish the regression model of the tunnel entrance slope displacement. Compared with other machine learning methods, LSSVM is more suitable for regression simulation under the condition of small data sets and has good generalization ability. Therefore, it is necessary to establish a time series prediction model. It can predict and warn the risk of large slope displacement based on the characteristics of slope displacement data at the tunnel entrance section11. Although these problems can be solved by “gradient pruning” or “unit door switch”34, LSSVM has a simple mathematical structure. It is more suitable for the initial stage of research on the applicability of multivariate time series in the complex structure of the tunnel entrance section.

Like other learning algorithms, the regression effect of LSSVM is also sensitive to the selection of key parameters. Grid search can solve this problem but its computational efficiency is low35,36. The random search method is a good choice, but the traditional random search process is easy to fall into the local optimal solution when solving complex optimization problems. Biological optimization strategy is a new type of random search method, which overcomes the shortcomings of local optimal solutions37. Using a more global and computationally efficient bacterial foraging optimization algorithm (BFOA), a BFOA-LSSVM hybrid intelligence method for displacement prediction of tunnel entrance slopes is established.

Multivariate time series model

LSSVM regression

Least squares support vector machine, LSSVM is a type of support vector machine38. It transforms the target optimization problem into a quadratic programming problem with equality constraints in the traditional vector machine method. This made the model calculation faster. For a set of known data samples \(\{ x_{i} ,y_{i} \}_{{i = 1...{\text{K}}}}\), where \(x_{i} \in R^{m}\) is an m-dimensional time series input sample, and \({\varvec{y}}_{{\varvec{i}}} \in R^{1}\) is a one-dimensional predict output. The LSSVM uses the non-linear mapping function \(\phi (x)\) to non-linearly map the sample to the high-dimensional space, and realizes the conversion of the non-linear function estimation problem in the original space to the linear function estimation problem in the high-dimensional feature space39,40:

$$f(x) = \omega^{T} \phi (x) + b$$
(1)

where \(\omega = [\omega_{1} ,...,\omega_{n} ]^{T}\) is the vector of weight coefficients, and \(\phi (.) = [\phi_{1} (.),...\phi_{n} (.)]^{T}\) is the mapping function.

This regression problem is transformed into an equation constraint problem through the principle of structural risk minimization, further transformed from constrained optimization into unconstrained optimization through Lagrangian equation, and finally into the solution of Lagrangian operator \(\alpha_{k}\) and paranoid quantity \(b\):

$$\left[ {\begin{array}{*{20}c} 0 & {\quad L^{T} } \\ L & {\quad \Omega + \gamma^{ - 1} I} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ {\alpha_{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ y \\ \end{array} } \right]$$
(2)

where \({\varvec{y}} = [y_{1} ,y_{2} ,...,y_{N} ]\) is the output array of training samples; L is an n-dimensional array, \({\varvec{L}} = [1,1,...,1]\); \({\varvec{\alpha}} = [\alpha_{1} ,\alpha_{2} ,...,\alpha_{N} ]\). \(\Omega = \phi (x_{k} )^{T} \phi (x_{l} ) = K(x_{k} ,x_{l} )\), \(k,l = 1,2,...,N\); \({\varvec{I}}\) is a unit vector; \(\gamma\) is a regular parameter representing the degree of interval fitting.

By solving formula (2) to obtain \(\alpha_{k}\) and \(b\), then the least squares vector machine model can be expressed as:

$$y(x) = \sum\limits_{k = 1}^{N} {\alpha_{k} K(x,x_{k} ) + b}$$
(3)

where \(K(x,x_{k} )\) is the kernel function, and the radial basis kernel function is used here: \(K(x,x_{k} ) = \exp \{ - \left\| {\left. {x - x_{k} } \right\|} \right.^{2} /\sigma^{2} \}\). \(\sigma^{2}\) represents the width of the kernel function and determines the final degree of fit.

For the dependence of LSSVM on the core parameters \(\gamma\) and \(\sigma^{2}\), the bacterial foraging optimization algorithm (BFOA) is used to find the optimal value, so as to establish a more accurate regression prediction model for the deformation of the tunnel entrance.

LSSVM evolved by BFOA

Bacterial foraging optimization algorithm (BFOA) is a random search algorithm. It draws on imitating the foraging behavior of human E. coli and improves the calculation function of the traditional random search algorithm, so that the random calculation process has a better globality and the search results are not easy to fall into the misunderstanding of the local optimal solution. For a minimum value problem, BFOA can achieve an effective solution without any gradient measurement or analysis37. The specific calculation process is as follows: First, S bacteria individuals are randomly generated within the value range of the parameters to be optimized, and each individual contains a set of numerical combinations of the parameters to be optimized. Each virtual bacteria is actually an experimental plan, which continuously moves on the functional surface (LSSVM) to find the optimal solution. After that, all bacteria perform \(N_{c}\) trending operations with the trending step size \(c(i)\), and perform replication operations when the minimum fitness value of the population does not meet the expected value. After repeating this process \(N_{re}\) times, the population migration is carried out with Ped as the control probability, and the maximum number of migrations is limited to \(N_{ed} {\kern 1pt}\). In this process, the fitness value refers to the error between the predicted result and the measured result when a parameter represented by a certain bacteria is used to calculate the test sample. Many methods can be used to evaluate this error. This study uses the root mean square error evaluation method:

$$Fv_{e} = \sqrt {[\sum\nolimits_{t = 1}^{{{\text{S}}_{{0}} }} {(y_{t} - y_{t}^{\prime } } )^{2} ]} /{\text{S}}_{{0}}$$
(4)

Among them, \(y_{{\text{t}}}\) and \(y_{t}^{\prime }\) respectively represent the predicted value and measured value of the test sample t, and \({\text{S}}_{{0}}\) is the test sample size.

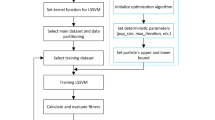
The logic of BFOA’s optimization of LSSVM parameters is shown in Fig. 1, through the iterative optimization of the key parameters \(\gamma\) and \(\sigma^{2}\), the regression ability of LSSVM in landslide risk prediction will be effectively improved. The specific process are as follows.

  • Step 1 Build an initial LSSVM based on the training samples, during which the core parameters of LSSVM are randomly generated.

  • Step 2 Evaluate the regression error of the current LSSVM by checking the sample. If it is less than the expected fitness value \(Fv_{\min }\), then perform step (9); otherwise, perform the BFOA process shown in step (3). In this study, \(Fv_{e} = 10^{ - 2}\).

  • Step 3 In a certain optimization interval, randomly generate an initial population containing \(2S_{r}\) individuals. In this study, the number of optimization targets is 2, then the population is in a two-dimensional space, and the coordinates of each individual bacteria represent the core parameters \(\gamma\) and \(\sigma^{2}\) of LSSVM, respectively. The selection of these two parameter optimization intervals comes from previous research on LSSVM parameter value suggestions and experience15,41. In this study, the optimization intervals are \(\gamma \in \left( {0,20} \right]\) and \(\sigma^{2} \in \left( {0,100} \right]\).

  • Step 4 Perform tendency operation. In the interval [-1,1], generate a random vector to adjust the position of each individual bacteria, compare the individual fitness values before and after the adjustment, and keep the bacteria individuals with smaller fitness values. Repeatedly perform a total of \(N_{c}\) trend operations, this study takes \(N_{c} = 10\).

  • Step 5 Perform replication operations. Sort the current population in descending order of fitness value, remove \(S_{r}\) individuals with larger fitness values, and copy the remaining individuals to keep the total population unchanged. Return to step 4 and record the number of copies \(N_{re} = N_{re} + 1\).

  • Step 6 Perform migration operation. When the number of copy operations reaches the maximum (\(N_{re\,\max } = 15\) in this study), destroy all bacteria in the current area, and randomly select other areas within the optimized interval to re-execute step 3. This operation aims to avoid the local optimal solution and keep the BFOA with good globality.

  • Step 7 When the migration operation reaches the expected limit, stop the iteration and record the minimum fitness of the current population. In this study, the upper limit of the migration operation is set to \(N_{ed\,\max } = 5\).

  • Step 8 Substitute the current position information of the individual into the LSSVM as the model parameter, obtain the root mean square error of the current model through the evaluation of the test sample, and use it as the fitness value of the current individual. Compare the global minimum fitness value \(Fv_{\min }\) with the expected fitness value \(Fv_{e}\), if \(Fv_{\min } \le Fv_{e}\), go to step (9); otherwise, return to step (3).

  • Step 9 Output the optimal parameters represented by the two-dimensional coordinates of the bacteria with the smallest fitness, and use them as the LSSVM parameters to establish an optimized regression model.

Fig. 1
figure 1

Implementation logic of BFOA-LSSVM hybrid model.

Full size image

Multivariate time series model

The time series prediction of slope is to predict the displacement on the (N + 1)th day based on the displacement results of 1 ~ N days at the monitoring position on the Nth day. Then the (N + 1) day predict data is used as the new input, and the displacement results of 2 ~ (N + 1) days are used to predict the displacement of the (N + 2) day, and so on to roll forward the predict. The reason for this is that the obtained displacement monitoring results can reflect the geological characteristics of the slope, the degree of disturbance, etc., and the displacement prediction in the next few days can be effectively realized according to the change law.

During the construction of the tunnel entrance section, the blasting excavation disturbance formed a series of fissure structures inside the slope, which led to the obvious influence of temperature and seepage environment on the slope displacement, and the possibility of large deformation and instability of the slope after a sudden temperature change or a large amount of rainfall is greatly increased. The displacement data of the slope change process affected by specific factors is not smooth and continuous, and ordinary time series are difficult to describe this feature. Therefore, using temperature (T) and rainfall (R) as input indicators, an multivariate time series model is formed as shown in Fig. 2.

Fig. 2
figure 2

Multivariate time series modeling principle.

Full size image

Figure 2 describes a multivariate time series model. It describes the long-term stability change process of the tunnel entrance slope after tunnel blasting construction, under the influence of natural factors such as temperature and rainfall. Of course, blasting construction is the main cause of slope displacement, but the influencing factors of blasting disturbance are more complicated. Factors such as the design of the blasting plan, the distance between the blasting construction surface and the monitoring location, and the effect of blasting implementation will all have varying degrees of impact41,42. Therefore, this paper uses the machine learning model to learn the law of historical slope displacement data to identify the impact of blasting factors, and does not regard it as a multivariate time series factor alone.

The model shown in Fig. 2 refers to using the displacement data of days 1 to N and the temperature and rainfall data of day N to predict the displacement of day N + 1, and so on to roll forward the forecast. In this process, natural factors such as temperature and rainfall are not predicted, but the natural factors measured on the previous day are used to predict the displacement change of the next day. There are two main reasons for this. On the one hand, accurate prediction of these natural factors is not easy to achieve. On the other hand, the influence of natural factors on the slope displacement is not instantaneous, but has a certain hysteresis43,44,45.

The BFOA-LSSVM is used to model and regression predict the multivariate time series mapping process shown in Fig. 2 to realize the prediction and early warning of the slope displacement risk of the tunnel entrance section46,47.

Engineering applications

Engineering situation

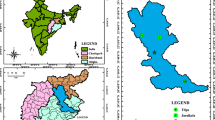
Wendong tunnel is located in the southwestern region of Yunnan Province, China, it is part of the Molin expressway. The entrance section of the tunnel has a steep slope of \(35^{ \circ } \sim 42^{ \circ }\). The geological environment of the engineering area is mainly mudstone and sandstone, and the geological longitudinal section is shown in Fig. 3. The tunnel is mainly located in moderately weathered sandstone and mudstone, and the surrounding rock strength is relatively high, so it needs to be constructed by mining method blasting. The survey found that there are a large number of mudstone interlayers or joint fissures filled by soft rock in the moderately weathered sandstone layer. Tunnel blasting caused these structures to be weakened or even destroyed, which directly affected the stability of the slope.

Fig. 3
figure 3

Geological section of Wendong tunnel entrance section.

Full size image

The elevation of the tunnel construction area is 1153.76 ~ 1398.21 m, with a relative elevation difference of 244.45 m. Groundwater consists of Quaternary soil layer pore water and bedrock fissure water, which is small in quantity, and is mainly recharged by atmospheric precipitation and surface water infiltration. June to October is the continuous rainy season in this area, and the average annual precipitation will reach 1112.0 ~ 1964.4 mm. The location of the tunnel and the slope of the entrance section are shown in Fig. 4.

Fig. 4
figure 4

Geographical location information of the project.

Full size image

Restricted by highway route planning, the exit section of the tunnel is at an angle of 40 degrees with the direction of the surface elevation line. During the construction process, the CD method was used for blasting excavation in four areas. The distance between the construction surface in each area along the tunnel axis was about 3 m, and the excavation speed was controlled to 1 m/d. Immediately after excavation, a 1 m-spacing I-steel arch and steel mesh were used to establish a flexible support system, and the distance between the construction surface of the overall second lining and the construction surface of No.IV tunnel was controlled to not exceed 30 m. The design of the blasting scheme is shown in Fig. 5. The last two figures in Fig. 5 are the construction process of the entrance section of Wendong Tunnel and the effect after the completion of the construction. The site investigation revealed that the tunnel blasting construction destroyed the stability of the original rock structure and caused a potential landslide in the area as shown in Fig. 6.

Fig. 5
figure 5

Design and construction of blasting scheme for the entrance section of Wendong tunnel.

Full size image
Fig. 6
figure 6

Contour line of Wendong tunnel entrance section and the layout of monitoring points.

Full size image

A series of hydrostatic level gauge and temperature and rainfall sensors are installed in the risk area, to monitor the surface settlement of the slope (the slope displacement mentioned in this study refers to its longitudinal deformation), temperature and rainfall index, which provides the data basis for the prediction of the slope deformation of the tunnel portal section.

The relationship between the location of the sensor and the tunnel is shown in Fig. 6. During the installation of the hydrostatic level gauge, steel bars and concrete platforms are used to ensure the stable connection between the instrument and the target stratum. At the same time, GPS positioning is used to ensure that the same set of measuring instruments is at the same elevation during installation. It should be noted that the GPS positioning tool is an instrument independent of the monitoring system. It is only used for height calibration during the installation of the hydrostatic level gauge to ensure that the sensor is installed on the expected contour. Because the monitoring target is the relative surface settlement value between the monitoring point and the reference point, the real elevation is not used here, but the GPS elevation.

Outside the potential landslide area, a hydrostatic level gauge reference point is arranged at a relatively stable location far enough away from the tunnel construction area (generally a location that is 3 times the tunnel diameter and is not affected by construction disturbance and has good stability). The reference point and the monitoring point are connected by a pipe and filled with measuring liquid. The surface settlement monitoring result refers to the elevation change value of each monitoring point relative to the reference point, and this value is derived from the hydraulic pressure change of the sensor caused by the surface deformation.

Take the φ95 four-core shielded cable to connect the aforementioned PY124B-226E hydrostatic level gauge sensors and temperature and rainfall sensors in parallel. According to the sensor grouping shown in Fig. 6, a total of 3 collection units are set up. Each acquisition unit collects the corresponding grouped sensor signals. These signals are transmitted to the transmitting unit through the RS485 short-range radio frequency module. The system uploaded to the internet through the USR232-730 GPRS module via the mobile phone communication signal. The data remote transmission unit is shown in Fig. 7.The server system obtains the monitoring data uploaded by the GPRS module in the form of network access as shown in Fig. 8. At the same time, the server system integrates a linear sliding function for data denoising processing, which can realize the processing of possible noise in the monitoring results. To be simplified, related literatures48,49 can be consulted for the specific steps of the denoising function.

Fig. 7
figure 7

Data remote transmission unit.

Full size image
Fig. 8
figure 8

IoT data transmission process.

Full size image

The system realizes the remote, real-time and automatic monitoring of information at the tunnel entrance. It can obtain accurate and equidistant surface settlement monitoring results and related temperature and rainfall information, which provides a data basis for the multiple time series predict and early warning of the deformation risk of the tunnel entrance section.

Monitoring data predict and early warning

Based on the monitoring of the internet of things (IoT), the time series prediction method is used to predict and warn the change trend of the monitoring data results. During the prediction process, the historical input data is set to 5 days. Taking the monitoring data of monitoring points 2–5 in Fig. 6 as an example, part of the learning samples of the time series model are shown in Table 1. Five groups of samples were randomly selected as test samples (marked by ‘*’ in Table 1), and the remaining samples were used as training samples. These samples are used to train the BFOA-LSSVM model, the key parameters can be obtained: \(\gamma = 3.784\) and \(\sigma^{2} = 0.257\). This set of parameters represents the regression model obtained by training. It should be noted that this set of parameters is actually trained after the training samples are normalized. The calculated output results of the model need to be inversed.

Table 1 Partial learning samples.
Full size table

On December 3, 2019, it was found that the data prediction results of points 2–5 showed a continuous downward trend, and the decline speed will gradually increase. According to the data rules, it is found that the position will reach 8.2 mm on December 4 as shown in Fig. 9, which exceeds the displacement control standard of this project. The zero point of the horizontal axis data in the figure represents the date October 28, 2019. According to the early warning situation, the engineering command department promptly carried out surface grouting and strengthening of tunnel support in the target area. After that, the measured data gradually stabilized at 7.9 mm on December 3, and the engineering risk was effectively controlled. The application results show that the method can accurately obtain the data change trend, and can effectively realize the early warning of large deformation disasters in the tunnel entrance section.

Fig. 9
figure 9

Project monitoring data predict and risk treatment.

Full size image

Historical data amount analysis in the time series

Reconstruct the learning samples with the data of sensors 2–5, control the number of historical input days as 3 days, 4 days, 5 days, and 6 days respectively. Roll forward the predict for 3 days (2019/11/25 ~ 2019/11/28), and the absolute error between the predicted result and the measured result is shown in Fig. 10.

Fig. 10
figure 10

Calculation errors under different historical data conditions.

Full size image

It can be seen that as the amount of historical input data increases, the prediction error gradually decreases (the contrast between different colors). When the number of historical days exceeds 5 days, this change is no longer obvious. In the actual application process, since the amount of historical data is limited, too many historical input days setting will result in a reduction of learning samples and loss of calculation cost, so the number of historical input days is determined to be 5.

Prediction accuracy analysis of different time periods

The learning samples in Table 1 are used to perform regression training on the LSSVM model, and the prediction is continuously rolled forward for 10 days. The prediction results and their errors are shown in Fig. 11. It can be seen that with the increase of prediction time, the prediction accuracy decreases significantly. The maximum prediction error reached 0.8 mm, and the growth process was rapid. For the model established in this study, this loss of accuracy is mainly due to the untimely update of natural factor information. Therefore, in order to ensure the accuracy of the prediction results, this study suggests that the prediction step is 1 day, and the learning samples are continuously updated according to the latest measured data information to obtain a better prediction effect50,51.

Fig. 11
figure 11

Effect of rolling prediction distance on the accuracy of results.

Full size image

Discussion

Firstly, the sensitivity of LSSVM parameters is discussed. Manually set different numerical combinations of \(\gamma\) and \(\sigma^{2}\) respectively, and perform trial calculations through the aforementioned model and test sample. The root mean square error of the calculation results of the test sample group under different parameter combinations is recorded, and the results are shown in Fig. 12. Among them, 12 is a three-dimensional distribution surface, and 13 is a two-dimensional contour map.

Fig. 12
figure 12

Three-dimensional surface.

Full size image

It can be seen that with the change of parameters, the regression error of LSSVM presents an irregular surface, and the parameter combination group with the smallest error presents a curved strip distribution. In this case, manual trial calculation or general parameter optimization methods are difficult to find the optimal parameter combination.

The calculation results also show that the grid search method is difficult to effectively obtain the optimal solution of the core parameters of LSSVM. Because for such a complex non-singular convergence surface, the mesh must be detailed enough to ensure that the grid points can fall into the optimal solution35,36. In addition, it is difficult to determine whether the current mesh is sufficiently detailed. At the same time, the grid search method will repeat the LSSVM modeling process a lot, resulting in low computational efficiency. The general random search algorithm can improve the calculation efficiency, but for the error distribution surface shown in Figs. 12, 13, the random search process is easy to fall into the local optimal solution. BFOA can solve the above problems well, and effectively realize the search for the optimal solution of the core parameters of LSSVM.

Fig. 13
figure 13

Two-dimensional contour.

Full size image

Sensitivity analysis of BFOA parameters

In order to improve the computational efficiency in the process of searching for the optimal solution of BFOA, an attempt was made to select the optimal solution for its key initial parameters.

Control the migration to remain \(C(i) = 0.3{\text{\% }}\) unchanged, and try to calculate the BFOA convergence curve under different approach length \(P_{ed}\) conditions, as shown in Fig. 14, and determine the optimal value of \(P_{ed} = 0.3\).

Fig. 14
figure 14

Influence law of approach length \(P_{ed}^{{}}\).

Full size image

Then, keeping \(P_{ed}^{{}} = 0.30\) unchanged, it is verified that when \(C(i) = 0.3{\text{\% }}\), as shown in Fig. 15. BFOA has the fastest convergence rate for LSSVM optimization.

Fig. 15
figure 15

Influence law of migration \(C(i)\).

Full size image

In the above process, the ordinate of the convergence curve is the root mean square error of the regression result of the test sample group.

Prediction accuracy verification of multivariate time series

As mentioned above, this study uses the two parameters of temperature and rainfall as additional inputs in the time series calculation process to participate in the prediction calculation, forming an multivariate time series model. In order to illustrate the effectiveness of this method, the data in Table 1 are used to compare the forecasting effects of time series considering different expansion factors. That is, only input1 ~ input6 in Table 1 are used as the input item of the learning sample (only consider temperature), or only input1 ~ input5 + input7 are used as the input item(only consider rainfall), and the output item is unchanged. In the calculation process, the number of historical input days is 5. The calculation results are shown in Fig. 16.

Fig. 16
figure 16

Multivariate time series prediction effect verification.

Full size image

It can be seen that the traditional time series prediction accuracy has been corrected at the time point when the training samples are updated. However, its prediction effect is not as good as the multivariate time series model within the rolling prediction distance, and the maximum error reached 1.21 mm. The accuracy of multivariate time series prediction results considering rainfall factors is significantly improved. After further considering the temperature factor, the predicted result tends to be consistent with the measured curve, and the slope displacement data obtained by the sensor monitoring is well reproduced, and the maximum error is only 0.38 mm.

Prediction accuracy verification of hybrid LSSVM

In order to further illustrate the advantages of the hybrid LSSVM algorithm used in this paper, it is compared with the GP and ANN methods which commonly used in geotechnical engineering. Table 1 are still used as the learning samples, and the optimal parameters of each algorithm are searched and calculated by the artificial grid method to ensure the fairness of the comparison process.

The error statistics of the slope displacement prediction results of different models are shown in Fig. 17. It can be seen that LSSVM has smaller calculation errors than other models, and the accuracy of the model optimized by BFOA has been effectively improved. It shows that the regression ability of this model is better than the GP and ANN methods in the time series analysis of the slope at the entrance of the cave. At the same time, it proves that the hybrid algorithm established in this study is effective.

Fig. 17
figure 17

Comparison of regression accuracy of different algorithms.

Full size image

Correlation analysis of multivariate time series factors

In this study, a multivariate time series model was established considering the influence of temperature and rainfall on the deformation of the tunnel entrance section. In order to evaluate the influence of these two natural factors on slope displacement, the sensitivity analysis of the two indicators of temperature and rainfall was carried out by taking the data prediction results of 2019-12-05 as an example. At this time, the input data is (-5.85, -6.17, -6.42, -6.88, -6.97, 15, 30), and the output data is 7.35. According to the actual temperature and rainfall data change interval of the project site, manually adjust the values of these two parameters in the input data, and record the corresponding prediction results, and obtain the statistical curve as shown in Fig. 18.

Fig. 18
figure 18

Sensitivity analysis of temperature parameters.

Full size image

It can be seen from Fig. 19 that the prediction model established in this study can well reflect the changes of natural factors. Among them, when the temperature is 10 ~ 25℃, or the rainfall is less than 40 mm, the change of natural factors has little influence on the slope displacement of the tunnel entrance section. However, when the natural factors exceed the aforementioned limits, their changes have a relatively severe impact on the slope displacement.

Fig. 19
figure 19

Sensitivity analysis of rainfall parameters.

Full size image

In order to illustrate the correlation between natural factors and the predicted target, the statistics obtained are shown in Fig. 18. The abscissa in the figure has the same meaning as in Fig. 5, and the ordinate is temperature, rainfall, and surface subsidence, respectively.

It can be seen from Fig. 20 that the surface subsidence rate is proportional to the rainfall. The rainfall at the two locations ① and ③ is relatively small, and the corresponding slope displacement change rate is slow. The growth rate of surface subsidence at two locations ② and ④ increases significantly with the increase of rainfall. On the 62nd day in the picture, the construction party implemented grouting and other reinforcement measures in the area, which changed the slope displacement trend of the tunnel entrance section, so the subsequent data were not counted.

Fig. 20
figure 20

Rainfall and slope displacement.

Full size image

Figure 21 shows that the temperature is inversely proportional to the slope displacement speed. The sudden increase in temperature indicated by the purple circle even caused a significant uplift on the slope surface shown by the red circle nearby. On the whole, the temperature in the first 30 days is generally above 20℃, and the slope displacement speed is slower at this time. Then the temperature mostly drops below 18℃ in the 31st to 60th days, and the displacement speed of the slope increases significantly at this stage. In order to illustrate this rule more clearly, the 20th to 27th days (the yellow area in Fig. 21) and the 51st to 56th days (the purple area in Fig. 21) were selected for comparison. The rainfall in these two areas is almost the same, the average value is about 10 mm/d, but the temperature in the yellow area is significantly higher than that in the purple area. At this time, the displacement rate of the slope in the purple area is obviously larger, indicating that the decrease in temperature in the natural environment of Yunnan, China will cause the increase in the displacement speed of the slope at the tunnel entrance section. The temperature change mentioned here refers to the natural environment within the range of 10℃ to 30℃.

Fig. 21
figure 21

Temperature and slope displacement.

Full size image

From the measured data shown in Fig. 18, it can be seen that two natural factors, temperature and rainfall, have obvious influences on slope displacement, and this influence has a certain hysteresis. That is, when the temperature or rainfall changes, the slope displacement trend will be gradually affected in the next few days, rather than a significant change on the day when the temperature or rainfall changes. This result verifies the correctness of the multivariate time series model established in this paper.

Conclusions

In this study, a hybrid intelligent model and multivariate time series method for the deformation prediction of the tunnel entrance section were established, and an engineering application example was used to illustrate the effectiveness of this method. The conclusions are as follows.

  1. 1.

    Through comparative analysis, it can be found that it is necessary to consider the influence of temperature and rainfall factors in the process of slope displacement prediction. Especially when the temperature is less than 10℃ or the rainfall is greater than 40 mm, the change of natural factors has a significant effect on the displacement of the slope at the entrance of the tunnel. In this case, it is suggested that the prediction and evaluation rate should be improved, and the project safety monitoring should be strengthened.

  2. 2.

    The regression ability of LSSVM in the time series analysis of the tunnel entrance slope is better than the GP and ANN models. It should be noted that the causes of slope displacement at the entrance of the tunnel are multifaceted and complex. Tunnel blasting construction will cause changes in the soil parameters of the slope at the entrance section. Fully considering this change is conducive to establishing a more robust time series prediction model.

  3. 3.

    The prediction model established in this study can perceive changes in natural factors, but it is assumed that the temperature and precipitation do not change abruptly, which makes the research results have certain limitations. For engineering construction areas with drastic changes in natural factors, how to accurately describe the temperature and rainfall in the next few days should be focused on in future studies.