Introduction

In light of the increasing frequency of extreme weather events and natural disasters worldwide, the issue of climate change, with an increase in carbon emissions at its core, has emerged as a prominent concern for all countries1. Carbon emissions are not only pertinent to ecological and environmental protection but also to socio-economic development. According to the Sustainable Development Goals (SDGs), integrating economic, social, and environmental development represents a pivotal concern in the transition towards a sustainable development trajectory. Carbon emission efficiency(CEE) is a crucial indicator for green, low-carbon economic development2, offering insights into the interrelationships between social employment, economic growth, carbon emission reduction, and other factors. In this context, systematic research of CEE is imperative for addressing global climate change and advancing the sustainable development of the economy, society, and environment.

As the world’s largest energy consumer and carbon emitter, China has assumed responsibility for carbon emission reduction and has demonstrated a commitment to the principles of sustainable development. At the 75th session of the United Nations General Assembly, China pledged to strive for peak carbon dioxide emissions before 2030 and carbon neutrality before 2060, known as China’s 3060 dual-carbon goal. As the largest developing country, China’s primary mandate is to achieve sustained economic growth and social advancement. However, the most significant challenge for China in this period is to navigate the complex relationship between environmental protection and economic and social development. Examining China’s efforts to promote the SDGs and studying the development characteristics and drivers of China’s CEE can contribute to the global carbon reduction process and provide insights into the sustainable development of developing countries.

Current studies of CEE concentrate on three key areas: measurement, spatial and temporal characterization, and influencing factors. Firstly, existing studies have calculated CEE at various scales, including national3,4, provincial5,6, city7,8,9, watershed10, and urban agglomerations11. While the DEA model12,13 remains an important method for measuring CEE, scholars have gradually chosen the SBM model to calculate it3,4 due to its shortcomings in measuring radial distance function efficiency. Secondly, many researchers analyzed CEE’s time-related and location-related correlation features through statistical methods and exploratory spatial analysis techniques, such as global Moran’s I and local Moran’s I14,15,16. Some scholars adopted using the Markov Transition Probability Matrix17 found that CEE in China exhibits a dynamic evolution characteristic of club convergence, and using the Kernel Density Estimation Method found uneven development of CEE in Yangtze River Delta cities in China18, with the phenomenon of polarization19. Finally, the studies on the influencing factors of CEE found that propelled by the evolution of informatization and digitization, developments in digital economies20, digital finance21, digital investments22, the enhanced growth of green finance23, and the seamless integration of digital finance and green technological innovation7, can significantly enhance the CEE of these cities. China’s low-carbon pilot policy24 and the carbon emissions trading pilot policy9 can enhance the CEE in pilot cities through technological advancement and energy structure optimization. Emerging green technology innovations, such as Carbon Capture, Utilization, and Storage (CCUS)25 and increasing adoption of renewable energy can markedly improve CEE. Additionally, urbanization26,27,28, environmental regulations29,30, income inequality31, and industrialization26 are also important factors influencing CEE.

Although research in the field of CEE is relatively abundant, few scholars have systematically analyzed its dynamic evolution characteristics and sources of spatial differences. In both global and Chinese scenarios, the advancement of CEE is contingent upon strategic planning and guidance at the higher levels of strategic planning and guidance at the higher levels of governance, as well as the implementation of development practices at the lower levels. The regional level is a pivotal platform for achieving national and even global SDGs32, and it is essential to conduct a comprehensive investigation into regional heterogeneity. In examining the spatial disparities within China’s CEE, most researchers have divided the country into three economic zones: eastern, central, and western. The eight comprehensive economic zones identified by the Development Research Center of the State Council represent a more detailed division of mainland China based on an analysis of the similarity between regional natural resource endowments and economic development levels. Zeng (2019)32 briefly compared the spacial differences in CEE among the eight comprehensive economic zones in a study with a sample of 30 provinces in China, but the underlying causes were not thoroughly examined. In addition, no studies have employed Chinese city-scale data to analyze the carbon emission efficiency of the eight zones. Moreover, few studies have adequately considered the non-stationarity of influencing factors in both space and time simultaneously. The majority of existing studies continue to employ spatial econometric models8,33, Tobit models3,23, and difference-in-differences(DID) models24,34.

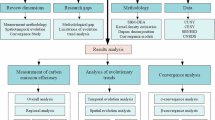
Accordingly, this paper takes 257 municipalities and cities in China from 2003 to 2019 as research samples and utilizes the Super-SBM model to measure the urban CEE. Combined with the zoning criteria of China’s eight comprehensive economic zones, the study initially examines the overall situation of China’s CEE and the characteristics of its center of gravity shift. Secondly, the sources of spatial differences in China’s CEE are analyzed using Dagum Gini Coefficient and Markov Transition Probability Matrix. Finally, the paper employs the spatio-temporal geographically weighted regression model (GTWR) to examine the CEE to investigate the influencing factors and the heterogeneity of their spatial distribution characteristics.

Research methods and models

Super-SBM model

This paper employs the Super-SBM framework introduced by Tone35 to evaluate the CEE of 257 Chinese cities from 2003 to 2019. The specific calculation formula is as follows:

$$\:{p}={min}\frac{\text{1}+\frac{\text{1}}{\text{m}}\sum_{i=1}^m\frac{\text{S}_i^x}{\text{x}_{i0}}}{\text{1}-\frac{\text{1}}{\text{S}_1+{S}_2}\left(\sum_{k=1}^{s_1}\frac{\text{S}_k^y}{\text{y}_{k0}}+\sum_{l=1}^{s_2}\frac{\text{S}_l^z}{\text{z}_{l0}}\right)}$$
$$s.t.\;x_{i0}\geq\;\sum_{j=1,\neq0}^n\lambda_j\;x_j-S_i^x,\forall\;i;$$
$$y_{k0}\leq\;\sum_{j=1,\neq0}^n\lambda_j\;y_j+S_k^y,\forall\;k;$$
$$z_{i0}\geq\;\sum_{j=1,\neq0}^n\lambda_j\;z_j-S_l^z,\forall\;l;$$
$${\text{1}-\frac{\text{1}}{\text{S}_1+{S}_2}\left(\sum_{k=1}^{s_1}\frac{\text{S}_k^y}{\text{y}_{k0}}+\sum_{l=1}^{s_2}\frac{\text{S}_l^z}{\text{z}_{l0}}\right)>\;0;}$$
$$S_i^x\geq\;0,\;S_k^y\geq\;0,\;S_l^z\geq\;0,\lambda_i\geq\;0,\forall\;i,\;j,k,l.$$
(1)

Where n represents the number of decision units, m signifies the number of input indicators, s1 corresponds to the number of desirable output indicators, s2 denotes the number of undesirable output indicators, \(\hbox {S}^{x}_{i}\) , \(\hbox {S}^{y}_{k}\) , and \(\hbox {S}^{z}_{l}\) represent their respective slack variables, and \(\lambda_{i}\) stands for the weight vector.

Dagum gini coefficient

This paper employs the Dagum Gini coefficient to assess the spatial disparities in the CEE. The Dagum Gini Coefficient and its subgroup decomposition method decomposes the overall Gini coefficient(G) into three components: the contribution of intra-regional variation to G(Gw), the contribution of inter-regional variation to G(Gnb), and the contribution of hyper-variable density to G(Gt)36. This decomposition satisfies G = Gw+Gnb+Gt. The formulas for the overall Gini coefficient (G), the intra-regional Gini coefficient(Gjj), and the inter-regional Gini coefficient(Gjh) are as follows37,38,39.

$$\:{G}=\frac{\sum_{j=1}^k\sum_{h=1}^k\sum_{i=1}^{n_j}\sum_{r=1}^{n_h}{\mid\;y_{ji}-\;y_{hr}\mid}}{\text{2}n^2\mu}$$
$$\:{G_{jj}}=\frac{1}{\text{2}\mu_j\;n^2_j}\sum_{i=1}^{n_j}\sum_{r=1}^{n_j}{\mid\;y_{ji}-\;y_{hr}\mid}$$
$$\:{G_{jh}}=\frac{\sum_{i=1}^{n_j}\sum_{r=1}^{n_h}{\mid\;y_{ji}-\;y_{hr}\mid}}{\text{n}_j{n}_h(\mu_j+\mu_h)}$$
(2)

Where \(\hbox {y}_{ji}\left({y}_{hr}\right)\) refers to the CEE of the region \(\hbox {i}\left(r\right)\) within the region \(\hbox {j}\left(h\right)\) . \({\upmu }\) is the average value of CEE of all regions, n and k represent the number of cities and regions, respectively (n = 257, k = 8). \(\hbox {n}_{j}\left({n}_{h}\right)\)is the number of cities included in the region \(\hbox {j}\left(h\right)\) , j = 1,2, … ,k.

Markov transition probability matrix

This paper employs Markov Transition Probability Matrix to examine the internal flow and probability transfer of CEE in Chinese cities across different time periods. A Markov chain is a discrete stochastic process, defined as a sequence of random variables in a given state space \(\left\{{X}\left({t}\right),{t}\;\;\in\;{T}\right\}\). The state of a random variable Xt+1 is only related to that of the variable Xt:

$$p\left\{{X}\left({t}\right)=\;j\mid\;X(t-1)=\;i,\;X(t-2)=i_{t-2},...,X(0)=i_{0}\right\}=p\left\{{X}\left({t}\right)=\;j\mid\;X(t-1)=\;i\right\}$$
(3)

Considering that regional productive and economic activities are often affected by neighboring regions40,41, scholars introduced the spatial lag into the traditional Markov transfer probability matrix and decomposed it into k matrices of order k×k, denoted as \(p_{{ij|\lambda }}^{{t,t+d}}\), which means the probability of the regional CEE transferring from the state i to the state j after d years under the condition that spatially lagged carbon emission efficiency of the region belongs to the state \(\lambda\) at that year. Comparing the value of the corresponding elements of the traditional and spatial Markov transfer probability matrix, whether the neighboring regions impact the local CEE transfer can be analyzed.

Geographically and temporally weighted regression model

By introducing a weight matrix based on spatial distance, the classical Geographically Weighted Regression (GWR) model improves the reliability of evaluation results at spatial scales in comparison to the traditional Ordinary Linear Regression (OLS) model. However, GWR is mainly used to explain spatial heterogeneity issues in cross-sectional data, and it may not fully account for the spatial heterogeneity of influencing factors across different periods in panel data42. To investigate how the influencing factors affect China’s CEE over time and space, this paper utilizes the GTWR model to capture the spatiotemporal variations in the regression coefficients of these factors45. The calculation formula of the model is as follows.

$$\:{Y}_{i}={\alpha\:}_{0}({\mu\:}_{i},{v}_{i},{t}_{i})+\sum\:_{k}{\alpha\:}_{k}({\mu\:}_{i},{v}_{i},{t}_{i}){X}_{ik}+{\epsilon\:}_{i}$$
(4)

Where, Yi is the dependent variable. Xik is the k-th explanatory variable, representing the local parameter estimate of the k-th explanatory variable for sample i.\(\:{\alpha\:}_{0}({\mu\:}_{i},{v}_{i},{t}_{i})\) is the intercept term. \(\:({\mu\:}_{i},{v}_{i},{t}_{i})\) denotes the spatio-temporal coordinates of the i-th city. \(\:{\alpha\:}_{k}({\mu\:}_{i},{v}_{i},{t}_{i})\) denotes the regression coefficient. \(\:{\epsilon\:}_{i}\)represents the random error.

Sample description and variable selection

Given the change in China’s governance approach to pollution prevention and overall process control with the introduction of the Clean Production Promotion Law in 200343 and the influence of global security events and changes in the international situation on global economic development and social life in 2019. Meanwhile, considering the objectivity and availability of data, this paper examines 257 Chinese cities from 2003 to 2019. This study explores the unique characteristics of China’s urban CEE across the temporal and spatial dimensions, focusing on the eight comprehensive economic zones shown in Table 144.

Table 1 Division of the Eight Comprehensive Economic Zones and their abbreviations.
Full size table

Since it is difficult to count the different energy consumption at the city level, the carbon emission data of cities in this paper was obtained by summing the county-level data from the China Carbon Accounting Databases (CEADs). Other data come from the China Statistical Yearbook, the CSMAR database, the EPS database, and provincial or municipal statistical yearbooks. Missing values were imputed by linear interpolation.

Dependent variable

Carbon Emission Efficiency (CEEit). Based on the available literature45, this paper constructs the CEE indicator system from input and output dimensions. Labor input uses the total number of people employed in the city’s primary, secondary, and tertiary industries. Capital input is accounted for using the perpetual inventory method46 to account for the fixed capital stock of the whole society. Energy input is characterized by the city’s total annual electricity consumption, which can more directly and accurately reflect the level of energy input in China47. The desired output is characterized by the city’s real GDP, calculated with 2003 as the base period. The undesired output is the city’s carbon dioxide emissions. The definitions of the input-output variables are provided in Table 2.

Table 2 Measurement Indicator System for China’s CEE.
Full size table

In Eq. (5), \(\hbox {K}_{it}\) represents the city’s fixed capital stock in period t, \(\hbox {I}_{it}\) represents the city’s fixed capital investment in period t, and \(\delta_{it}\) represents the depreciation rate (9.6%). Furthermore, based on the study by Cooper et al.48. This study investigates the efficiency of decision-making units and the amounts of inputs and outputs, as indicated in Eq. (6).

$$\:\text{N}\ge\:\text{M}\text{a}\text{x}\left\{\text{M}\text{*}\right(\text{R}+\text{V}),3\text{*}(1+\text{R}+\text{V}\left)\right\}\:$$
(6)

Where, N = 257 denotes the number of decision-making units. M = 3, R = 1, and V = 1 indicate the amounts of inputs, desired outputs, and undesired outputs, respectively. The result demonstrates that N = 257 > Max{3*(1 + 1), 3*(3 + 1 + 1)}=15, which suggests that the selection of decision-making units and the quantities of inputs and outputs in this research are justified. This implies that the measurement findings of CEE in this paper possess a certain level of coherence and scientific validity.

Independent variables

This paper selected seven independent variables from the social, economic, and environmental aspects. (1) Environmental regulation (ERit) is measured by the entropy weight method. The comprehensive evaluation index system is constructed with industrial wastewater, industrial sulfur dioxide, industrial fume (dust) emission, and the proportion of industrial pollution control investment in the value added of secondary industry49,50,51. (2) Energy consumption intensity (EIit) is represented by the ratio of annual electricity consumption to GDP52. (3) Population density (PDit) is indicated by the population per square kilometer53. (4) Urbanization rate (URit) is represented by the proportion of the urban population to the total population of the city54. (5) Industrial structure (ISit) is expressed by the ratio of the value added by the tertiary industry to that of the secondary industry55. (6) Openness level (Openit) is characterized by the proportion of a city’s annual import and export volume to the regional GDP16. (7) Green finance index (GFIit) is measured by the entropy weight method. The comprehensive evaluation index system is constructed with green credit, green investment, green insurance, green bonds, green support, green funds, and green rights56. The descriptive statistical analysis of the variables is provided in Table 3.

Table 3 Descriptive statistics of variables.
Full size table

Results analysis

Measurement of Urban CEE

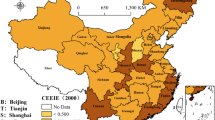
Based on the average value of the urban CEE in the study period, this paper utilizes ArcGIS10.8 software to illustrate the spatial distribution of the CEE in China, as shown in Fig. 1.

Fig. 1
figure 1

Spatial Distribution of CEE of Cities and Eight Comprehensive Economic Zones in China (Drawn by the authors).

Full size image

In 2019, China’s urban CEE improved by 24.79% compared to 2003, with an average annual growth rate of 1.46%. The growth has been consistently upward, characterized by a spatial distribution pattern of the north is higher than the south, the east is higher than the west, and the coast is higher than the inland.

When examining the regional divisions of the East, Central, and West, the average efficiency value of the eastern cities maintained at about 0.380, and the gap between the eastern and the central and western regions, whose average values remained essentially unchanged at around 0.320, has progressively widened, influencing the entire country. One potential explanation is that following the financial crisis in 2008, the coastal cities in the east gained an advantage due to their geographical location. It allowed them to quickly access up-to-date information, focus on advanced technology and significant capital, and expedite the growth of manufacturing and service sectors. Consequently, this support played a crucial role in promoting energy efficiency and reducing emissions57.

From the perspective of the eight comprehensive economic zones, the CEE average values from high to low are as follows: Southern Coastal > Northeast > Southwest > Eastern Coastal > Middle Yangtze River > Northern Coastal > Middle Yellow River > Northwest. The reason may be that the climate and geographic conditions of the Southern Coastal Economic Zone are more favorable for the utilization of renewable energy, such as wind energy and solar energy58, coupled with the adequate guidance of regional policies to reduce the intensity of carbon emissions, such as the relevant policies introduced by Hainan Province to promote clean energy vehicles59,60,61. The Northeast Economic Zone’s transition process of the development mode of high-energy-consuming industries to low-carbon industries like services and light manufacturing has boosted energy efficiency, clean energy, and carbon reduction technologies. The Southwest Economic Zone’s development and utilization of clean energy sources like hydropower and natural gas also play a role in the differences in carbon emission efficiency among economic regions.

Moreover, to examine the spatial movement patterns of China’s CEE, this study illustrated the displacement path of the urban CEE’s center of mass using five specific time points, specifically, 2003, 2005, 2010, 2015, and 2019 (Fig. 2). During the study period, the urban CEE center of gravity in China has shifted towards the northeast, with coordinates ranging from 113.875°E to 115.421°E and 31.562°N to 32.234°N. This indicates that the average CEE in northeastern cities was higher than in southwestern cities62. Furthermore, the focal point of the carbon emission efficiency distribution in China relocated towards the northeast, starting from Suizhou City in Hubei Province and extending to the outskirts of Xiaogan City. Subsequently, it further shifted northeastward to the northeastern region of Xinyang City in Henan Province. The heavy industry in China’s northeast region, which was once the main industrial base, has shifted to the southeast coastal region due to industrial structure adjustment and environmental protection policies. This shift, along with changes in energy structure, has resulted in a shift in the energy center of gravity, consequently impacting China’s CEE center of gravity. In China, the cumulative migration of the center of gravity of CEE has shifted approximately 164.241 km towards the northeast. The distance towards the east (134.65 km) surpasses the distance towards the north (91.97 km), suggesting that the predominant migration of the center of gravity of CEE occurs laterally. This observation confirms the geographical pattern of divergence from east to west.

Fig. 2
figure 2

Trajectory of center of gravity shift in China’s CEE (Drawn by the authors).

Full size image

Spatial disparities and source decomposition of CEE

Overall differences in Urban CEE

Table 4 reveals that throughout the study period, the Dagum Gini coefficient demonstrates a decline in the overall CEE Gini coefficient of China from 0.259 to 0.241, with an average annual decrease rate of 0.41%. Additionally, the mean value of 0.189 highlights a notable disparity in China’s CEE.While the overall Gini coefficient exhibits relatively stable, it still displays a phased pattern of decline followed by an increase. The decline phase is from 2003 to 2013, with an average annual decline rate of 3.69%, and the increase phase is from 2013 to 2019, with an average annual growth rate of 8.07%.

Table 4 The overall and Intra-differences Gini coefficients of CEE in China’s eight Comprehensive Economic zones.
Full size table

Intra-differences in urban CEE among the eight comprehensive economic zones

The Northern Coastal, Northeast, and Eastern Coastal economic zones exhibit the highest intra-regional differences in CEE, surpassing the national mean value of 0.158, as indicated by the mean Intra-Differences Gini coefficients of each economic zone.Following that, it proceeds with the economic zones of Northwest, Southern Coastal, and Middle Yellow River, while the economic zones of Southwest and Middle Yangtze River exhibit lesser disparities, with coefficient values below 0.135.

When examining the shifting patterns in the Gini coefficients across the eight extensive economic zones, it is evident that the Northwest Economic Zone encounters the most significant disparities within the CEE region. This is characterized by an average yearly reduction rate of 2.62%. The Middle Yellow River and Northern Coastal economic zones come after it, with average annual decrease rates of 1.07% and 1.40% correspondingly. On the other hand, the Northeast Economic Zone exhibits the smallest disparity within the region, boasting an average yearly growth rate of 0.52%. It indicates that the intra-regional differences and changes in CEE within the Northern Coastal and Northwest economic zones were considerable during the study period, while the Northeast Economic Zone had the slightest fluctuations despite its significant internal differences.

In summary, the development of CEE variations among the eight comprehensive economic zones had distinct features. At the end of the study period, however, each economic zone showed an increasing tendency towards intra-regional disparities.

Inter-differences in urban CEE among China’s eight comprehensive economic zones

In China, the graph in Fig. 3 presents the average Gini coefficient of Inter-Differences, and the trend in the eight comprehensive economic zones over time. Firstly, comparing the average values of Inter-Differences coefficient reveals significant inter-regional variations between the Northern Coastal, Middle Yangtze River, Southwest, Northwest, and Southern Coastal economic zones, and between the Northeast Economic Zone and Middle Yangtze River and Southwest economic zones. The remaining economic zones display relatively minor inter-regional disparities. Moreover, the Northern Coastal and Northwest economic zones emerge as outliers due to their significant disparities in comparison to other zones. This can be attributed to the fact that these two zones represent the opposite ends of China’s regional development. The Northern Coastal Economic Zone occupies outstanding locational advantages, and its economic and industrial development and opening-up level are ahead of the other zones. However, the specific geographic features and natural conditions of the Northwest Economic Zone constrain its economic growth, industrial optimization, and urbanization, consequently affecting CEE. Moreover, despite the significant decrease in the Inter-Differences Gini coefficient in 2015, all of them experienced varying degrees of increase by the end of the research period. It means that the inter-regional disparities in CEE among the eight comprehensive economic zones in China exhibited a pattern of initially fluctuating downward and then fluctuating upward throughout the study period.

Fig. 3
figure 3

Evolution trends of the average inter-difference Gini coefficient of the CEE among the eight comprehensive economic zones (Drawn by the authors).

Full size image

Spatial sources of CEE differences among eight comprehensive economic zones

Table 5 shows that the mean values of the intra-regional, inter-regional, and hyper-variable density coefficients are 0.024, 0.096, and 0.070, respectively. The mean values of these contributions are 12.49%, 50.57%, and 36.94%, respectively. It indicates that the inter-regional differences among the eight economic regions are the primary spatial source of China’s CEE divergence.

Table 5 Decomposition of the spatial sources of China’s CEE divergence.
Full size table

Analysis of the dynamic evolution of urban CEE

Based on the calculation of urban CEE, this paper divides the efficiency values into four states: low efficiency, lower efficiency, higher efficiency and high efficiency, and analyzes the transfer characteristics of each state with Markov transition probability matrix. For ease of analysis, this paper refers to CEE transfers within neighboring countries as “upward transfers” or “downward transfers”, and to transfers across neighboring countries as “upward skipping transfers” or “downward skipping transfers”.

Traditional markov transition probability matrix

From 2003 to 2019, Table 6 presents the Markov transition probability matrix illustrating the urban CEE in China. The probabilities of low-efficiency, lower-efficiency, higher-efficiency, and high-efficiency cities maintaining their current efficiency states are 90.3%, 55.3%, 51.7%, and 92.0%, respectively, indicating a high likelihood of China’s cities maintaining their current level of carbon emission efficiency due to the clustering of low-efficiency and high-efficiency. Secondly, the non-diagonal elements are all smaller than the main diagonal elements, further confirming that the development of CEE in China’s cities is stable. Meanwhile, when examining the elements on both ends of the diagonal, it is evident that the likelihood of upward movement for each state is greater compared to the likelihood of skipping upward or moving downward. In particular, there is a 7.9% chance of transitioning from the low-efficiency state to an upward state, while the combined probabilities of skipping upward transitions amount to 1.8%.The likelihood of a higher-efficiency state being reached through upward transfer is 24.1%, while the probability of skipping upward to a higher state is 5.1%. Additionally, there is a 15.6% chance of experiencing a downward transfer. The likelihood of a higher-efficiency state moving upwards is 26.7%, while the combined probabilities of downward transfers amount to 21.6%. The total likelihood of the high-efficiency state transitioning downwards to the other states is 8.0%.That indicates China’s urban CEE is a gradual and phased improvement process.

Table 6 Traditional Markov transfer probability matrix for China’s CEE.
Full size table

Spatial markov transition probability matrix

The spatial correlation analysis in this study used the Inverse Distance Squared Matrix to evaluate the potential influence of spatial factors on urban CEE in China. The results presented in Table 7 demonstrate that the global Moran’s Index has consistently demonstrated positive values each year, indicating a substantial spatial correlation in China’s urban CEE. This aligns with the characteristics of both low-efficiency clustering and high-efficiency clustering observed in the traditional transition probability matrix.

Table 7 Global Moran’s I Index of China’s CEE.
Full size table

Moreover, this research employs the spatial Markov transition probability matrix to examine the reciprocal impact among urban areas. Table 8 findings indicate that spatial factors significantly impact CEE in Chinese cities. Neighboring cities in low-efficiency or high-efficiency states exert adverse or favorable spatial spillover effects on surrounding cities, respectively. However, the aforementioned spatial spillover effects are insignificant when neighboring cities are in lower or higher efficiency states.In other words, neighboring cities in a moderate-efficiency state have a relatively minor impact on the transition of states in surrounding cities.

For example, when neighboring cities are in low-efficiency states, compared to the conventional Markov transition probability matrix, the probability of maintaining the current state for each state changes by 2.4%, 17.9%, -1.7%, and − 3.7%. Meanwhile, the total probabilities of downward transfer of the higher-efficiency and the high-efficiency states increase by 3.3% and 1.1%, respectively. It indicates that the lower-efficiency neighboring cities will constrain the improvement of CEE in cities, increasing the probability of surrounding cities maintaining or upward transferring to lower-efficiency states.

In the context of a global view of the spatial Markov transition probability matrix, as the efficiency state of neighboring cities improves, the probability of surrounding cities maintaining low-efficiency states decreases, and maintaining high-efficiency states increases. It implies that the high CEE of neighboring cities will reduce the probability of local regions remaining in lower states and improve the CEE of neighboring, especially those in the higher-efficiency states. Therefore, besides the influence of the efficiency states of neighboring cities, the local state is also an essential factor affecting the improvement of urban CEE. When improving urban CEE, it is necessary not only to consider the spatial spillover effect of neighboring cities but also to pay attention to the development of the CEE of cities themselves.

Table 8 Spatial Markov Transition Probability Matrix of China’s CEE.
Full size table

Analysis of influencing factors of urban CEE

Due to the spatio-temporal non-stationarity of China’s urban CEE, each influencing factor contributes differently to the CEE in different periods. This research examines the factors that influence China’s urban CEE and its spatio-temporal heterogeneity based on the eight comprehensive economic zones, utilizing the GTWR model as discussed by Huang63.

The VIF test results show that VIFmax is 1.47, and VIFmean is only 1.28, suggesting that the model does not have covariance issues. Furthermore, the test results for spatiotemporal non-stationarity presented in Table 9 demonstrate that the GTWR model exhibits a strong level of fitness, enabling enhanced analysis of the data in terms of space and time.

Table 9 Spatiotemporal non-stationarity test results for various models.
Full size table

Temporal evolution analysis of influencing factors of urban CEE

This paper initially evaluates the significance of the GTWR model’s analysis results, taking into account the approach used by Li et al.64. According to Table 10, the explanatory variables produce significant results above 92%, 90%, and 85% at the confidence levels of 10%, 5%, and 1%, respectively. It suggests that the analysis results possess a strong interpretation.

Table 10 The significance statistical results of regression coefficients for influencing factors.
Full size table

To visually demonstrate how the regression coefficients for different influencing factors change over time, this paper plotted the box line diagram of the coefficients over time using Origin2023b software, as shown in Fig. 4. ER, GFI, IS, and Open can enhance CEE in China. Environmental regulation can force industrial structure optimization and technological innovation to promote energy saving and emission reduction65. Green finance promotes green transformation of economic development by innovating low-carbon technologies66, reducing financing costs67, and guiding industrial development68. Optimizing and upgrading industrial structures can reduce energy consumption69 and carbon emission intensity70. Opening up to the outside world not only helps to introduce green production technology, equipment, and management experience69, but the financial income generated can also provide financial security for local green and low-carbon development71. EI and UR hinder the improvement of urban CEE. In promoting rapid economic and social development, urbanization also leads to the crowding effect of population concentration72,73. PD inhibits and then promotes carbon efficiency, shifting from the crowding effect74 to the scale effect75. In addition, with the different degrees of promotion or inhibition of influencing factors, the differences in the degree of contribution of PD and UR to CEE of different cities gradually increase. EI and GFI show a decreasing and then increasing trend in the degree of contribution to CEE in various cities. The trend of the other factors is relatively stable.

Fig. 4
figure 4

Temporal Evolution Trends of the Regression Coefficients of the Influencing Factors (Drawn by the authors).

Full size image

Spatial heterogeneity analysis of influencing factors of urban CEE

In order to effectively represent the variation in space and time of each factor’s impact on the CEE of Chinese cities, this paper utilizes ArcGIS 10.8 software to plot the spatial distribution of the mean values of the regression coefficients of each influencing factor in the study period (Fig. 5), and Origin2023b software to illustrate the temporal trends of the regression coefficients of each influencing factor in the eight comprehensive economic zones (Fig. 6).

Fig. 5
figure 5

Spatial distribution of the average regression coefficients of the influencing factors (Drawn by the authors).

Full size image
Fig. 6
figure 6

Evolution trends of the influencing factors’ regression coefficients in the eight comprehensive economic zones (Drawn by the authors).

Full size image

In the Northeast, the effects of ER and EI are more pronounced. In the early period (2003 ~ 2013), environmental regulations significantly impacted the CEE of the Northeast Economic Zone. It may be since, as an old industrial base, the regional government had already adopted a series of regulatory measures to promote energy conservation and emission reduction in the Strategic Plan for the Revitalization of Old Industrial Bases in the Northeast Region and Other Areas76. In the later period(2012 ~ 2019), the role of energy intensity on the CEE of the Northeast Economic Zone shifted to a facilitating effect. It may be because China’s Northeast Revitalization strategy entered a new phase in the 12th Five-Year Plan period (2011 ~ 2015), and the optimization of government governance provided favorable conditions for introducing and collecting local talents, which improved labor productivity and affected the CEE77.

In the western region, the factors show spatial heterogeneity in the direction and degree of influence. ER exerts a green paradox effect78 on the CEE of the Northwest Economic Region in the late period. EI shows the most significant inhibition on the CEE of the Southwest Economic Region, which is may because a large amount of clean energy produced in the Southwest Region, such as hydropower and natural gas, cannot be adequately absorbed by local and brings more energy consumption in the process of west-to-east power transmission and west-to-east gas transmission. UR and Open have the most significant inhibiting effect on the CEE of the Northwest Economic Region. It may be because the Northwest Economic Zone is sparsely populated and ecologically fragile, and urbanization requires large amounts of energy input for infrastructure construction, production, and living79. Besides, the economic structure of the zone is mainly based on high-carbon energy and heavy industry, and opening up to the outside world may make it easier to attract carbon-intensive ones80.

In the coastal region, GFI significantly contributes to the CEE in the southern coastal zone. The green financial reform and innovation initiatives there have made the integration and development of financial and new energy industries a mission, promoting the green and low-carbon transformation of the region81. The opening up has a remarkable impact on the CEE in the eastern and northern coastal zones. This region is China’s economic and innovation development highland, which is more likely to absorb the new technologies introduced by opening up to the outside world and be able to utilize them in regional green development practices.

Conclusions and recommendations

This paper studies the spatial differences, development characteristics, influencing factors, and their spatiotemporal non-stationarity of the CEE in China’s 257 cities from 2003 to 2019 under the SDGs, based on the spatial division of the eight comprehensive economic zones. The contribution of this paper is, firstly, to refine the spatial division of the study area from the three traditional economic zones to the eight economic zones and to study the spatial differentiation pattern of cities’ CEE in a more detailed and systematic way, which can help Chinese economic zones to improve CEE in a targeted way. Second, this study comprehensively considers the non-stationary pattern of spatial and temporal changes of factors affecting CEE, which helps to clarify the spatial and temporal differences in the impact of each factor and helps regional governments seize development opportunities and promote sustainable development in line with the trend.

The main conclusions are as follows. (1) The CEE of Chinese cities shows an overall upward trend during the study period, with the center of gravity shifting to the northeast. The CEE of the southern coastal, northeastern, and southwestern economic zones is higher than others. (2) Both intra- and inter-differences in CEE of the eight comprehensive economic zones show an increasing trend at the end of the study period. The inter-differences among the eight zones represent the primary spatial source of CEE divergence. (3) The CEE of Chinese cities is a gradual improvement process. The low or high efficiency status of neighboring cities will have negative or positive spatial spillover effects on neighboring cities, respectively. (4) Environmental regulation, energy consumption intensity, and green financial index remarkably influence the CEE, with significant spatial heterogeneity in the direction and intensity of influence.

Based on the above conclusions, the paper recommends the following policies: First, narrow the development gap between regions. Let developed zones drive the development of less-developed areas. Promote the diffusion of eastern green and low-carbon technologies, talents, and development experience from the coast to the inland to narrow the gap between China’s interregional socio-economic development and energy conservation and carbon reduction. Improve the efficiency of carbon emissions across the region by optimizing the resource allocation structure and sharing channels between areas. Second, implement regional fine-tuned management. Encourage local governments to effectively utilize local economic, social, and environmental resources to formulate regional sustainable development plans that are differentiated and targeted. For instance, in the northeast economic zone, it is required to strengthen environmental regulations and promote industrial restructuring appropriately. For the southwest economic zone, it is necessary to accelerate the development of green finance and reinforce technical research on clean energy development and consumption, thus facilitating sustainable development in China and the world.