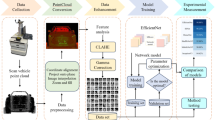
Abstract
The traditional airborne LiDAR point clouds vehicle recognition algorithms only utilize the contained geometric information and are not sufficient to recognize vehicles accurately, especially in complex urban scenes. And their applicability in super-high density UAV-LiDAR point clouds is unknown. Therefore, a 3-D algorithm combining geometric and intensity information from super-high density UAV-LiDAR point clouds is presented. The proposed algorithm firstly converts the original point clouds into a 3D multivalued image which fuses intensity, elevation and density information simultaneously. Thereafter, the potential vehicle voxels are extracted according to the intensity, elevation and density consistency of vehicles. Subsequently, individual vehicles are recognized using the potential vehicle voxel’s spatially connected set with vehicle size constraint. Finally, the quantified attribute information of each individual vehicle, containing the spatial location, type, and size, is determined. The results for recognized vehicles are evaluated using UAV-LiDAR data with different densities and demonstrate an average quality (Kappa coefficient) of 96.58% (96.04%) without being significantly affected by occlusion and the very close vehicle arrangement.
Similar content being viewed by others
Introduction
Vehicle recognition involves identifying vehicles and determining the type, location and (total or categorical) number of vehicles in a given area1. The recognized type, spatial location and distribution information of vehicles is an essential indicator of urban traffic and human activities and is vital in many applications, such as traffic flow estimation, traffic monitoring, traffic control and management modeling based on the vehicle categories, urban planning, real estate management, and disaster rescue2,3. Research on automatic vehicle recognition algorithm has attracted more and more attention. Nevertheless, vehicle recognition is still complex and challenging due to the diversified vehicle types and appearances, frequent occlusion by trees or lighting posts, uneven distribution of LiDAR points, interference of other similar artificial objects, and class imbalance problem.
Compared with traditional vehicle recognition based on surveillance camera4,5 or optical remote sensing6,7, the main advantages of Unmanned Aerial Vehicle-Light Detection and Ranging (UAV-LiDAR) lie in that:
-
(1)
It can directly, actively and quickly acquire ultra-high resolution three-dimensional (3-D) point clouds and their laser reflection intensity of vehicles and their surrounding environment over large-scale urban scenes. The topological, geometric, spectral and structural information contained in point clouds makes it show great potential for large-scale and high-precision recognition of vehicles.
-
(2)
LiDAR pulses can “penetrate” tree canopy, vehicles beneath trees could also be measured by LiDAR and thus the completeness of vehicle recognition can be further improved. For the above reasons, vehicle detection/recognition based on LiDAR point clouds gradually becomes a new research hotspot in recent years. Many approaches have thus been proposed by researchers.
Existing approaches on vehicle detection/recognition from LiDAR point cloud can be typically divided into image processing-based and segmentation-detection-based approach. The former firstly transforms the original or filtered point clouds into height grid data, thereafter various image processing operations are adopted to differentiate vehicles, such as thresholding1,8, mean shift segmentation and rule base classification9, watershed segmentation9,10, morphology based connected component analysis8, Marked Point Process11, rule combined with Laplacian of Gaussian detection12, and machine learning1,13,14. The latter firstly partitions original or filtered point cloud into significative segments approximating various objects, thereafter vehicle segments are isolated based on the designed rule consisting of different features11,15,16. For example, Toth et al.17 uses both height and width features. Zhang et al.18 and Eum et al.19 both combine the three features of area, rectangularity and elongatedness. Zhang et al.20 and Kan et al.21 both adopt the shape feature (2D vertical profile curve). However, the approaches described above have several limitations: Firstly, grid data creation, which requires projection and interpolation processing, may lead to information loss, especially in complex urban scenes where vehicle is occluded by other objects22. This may affect the integrity of the vehicle recognition result. Furthermore, image processing-based approach can only detect the roof of vehicles and obtain their 2-D geometric attributions and cannot support the application requirements of 3D vehicle reconstruction. Secondly, the above approaches are specifically focus on the utilization of geometric features. However, as mentioned earlier, the recognition based on geometry requires prior knowledge about the appearance of vehicle bodies21. This leads to the accuracy of vehicle recognition is sensitive to shape information of vehicles, and thus unable to cope with complex urban scenarios, especially in areas where vehicle point clouds are partially absent and uneven. Finally, almost all the algorithmic verification is carried out on manned airborne LiDAR datasets with the average point density of 1.5 ~ 40 points/m2, their applicability in super-high density UAV-LiDAR point clouds with point density bigger than 100 points/m2 (Karel et al., 2020 22; Point Cloud Catalyst (PCC) software (https://blog.csdn.net/Yang_Wanli/article/details/119491089)) is unknown and the algorithm for recognizing vehicles based on super-high density UAV-LiDAR point clouds has not been reported.
To resolve these restrictions, a 3-D vehicle recognition algorithm from super-high density point clouds combining intensity and geometrical information is presented. The proposed algorithm firstly converts the original point clouds into a 3-D multivalued voxel structure fusing intensity, elevation and density information simultaneously. Thereafter the potential vehicle voxels are extracted according to the elevation, density and intensity consistency of vehicles. Subsequently, individual vehicles are recognized using the potential vehicle voxel’s spatially connected set with vehicle size constraint. Finally, the quantified attribute information of individual vehicles, containing the spatial location, type, and size, is determined. The primary contributions of this work are: (1) a 3-D algorithm solving the problem of vehicle recognition from super-high density UAV-LiDAR point clouds is presented. (2) A scheme for combining UAV-LiDAR intensity and geometry information for accurate vehicle recognition is prevented. Intensity information is unrelated to the vehicle geometry and uneven distribution of point clouds, which makes it less sensitive to complex urban scenes.
Methodology
A given UAV-LiDAR point cloud dataset is a finite collection of laser points in 3-D space and is denoted as P,
where i is the index of laser points, N is the total number of laser points, pi represents the ith laser point, (xi, yi, zi) represent the coordinate positions of ith laser point along X, Y and Z axes in the Cartesian system, Ii is the laser reflection intensity value of ith laser point. Point cloud itself can be directly used to recognize vehicle. However, it is unstructured and does not explicitly represent topological and spatial-structure information between LiDAR points. This increases the difficulty of designing algorithm for recognizing vehicles. Furthermore, the recognized point clouds of individual vehicles cannot be directly used to represent the vehicle geometry. To solve these problems while supporting high-precision 3-D extraction of different types of vehicles, P is first regularized into a 3-D multivalued voxel structure which simultaneously fuses the intensity and geometric information contained in P. Then, the potential vehicle voxels are extracted based on the intensity and geometric consistency of vehicles. Finally, individual vehicle is recognized using the potential vehicle voxel’s spatially connected set with vehicle size constraint. And the quantified attribute information of each individual vehicle is determined, containing the spatial location, type, and size information.
Structuring LiDAR point cloud into a 3-D multivalued Voxel structure
-
(1)
Scene volume determination. An axis-aligned bounding box (AABB) is used to determine the scene volume of P.
where (xmin, ymin, zmin) and (xmax, ymax, zmax) are the minimum and maximum of x, y and z-coordinates of outliers removed laser points, xmin (ymin, zmin) = min {xi’ (yi’, zi’), i’ =1, …, N’ }, xmax (ymax, zmax) = max {xi’ (yi’, zi’), i’ =1, …, N’ }, i’ and N’ are the index and total number of outliers removed laser points, respectively.
-
(2)
Scene volume discretization. The AABB is discretized in 3-D space according to the voxel size (Δx, Δy, Δz). The spatial distribution characteristics of objects at different voxel size are different, and the accuracy of objects separation based on the above characteristics is also different. Therefore, the application-oriented optimal value of voxel size must be determined to ensure the accuracy of vehicle recognition. The effect of voxel sizes on vehicle recognition result and the optimal value will be determined in the “Experimental results and discussions” Section. Depending on the optimal voxel size, AABB is divided into uniform 3-D voxels, and the voxel collection is denoted as V,
where j is the index of voxels, M is the number of voxels, vj represents the jth voxel, (rj, cj, lj) represent the grid coordinates of jth voxel along row (R), column (C) and layer (L) axes in the resulting 3-D grid, Wj is the voxel value of jth voxel and will be assigned in the following quantization process.
-
(3)
Voxel value quantization. Each laser point in P is allocated to an individual voxel of the resulting 3-D grid using the following Eq.
After that, the value of a voxel containing laser point(s) are assigned the feature vector (w1, w2, w3) composed of the mean intensity, mean elevation, and mean density, whereas the value of a containing no laser point are assigned (0, 0, 0) representing “air”. Where mean intensity (elevation, density) denotes the average intensity (elevation, density) across all laser points inside a voxel, density23 denotes the number of laser points in a certain neighborhood centered on each laser point.
Further, to eliminate the unit and scale differences among the above different types of features, dimensionless processing is carried out. Standardization is firstly adopted to put different features on the same scale through Eq. (5), and then the standardized features are further discretized to {0,1, …, 255} by using Eq. (6).
Where e is the feature index, e = 1, 2, 3, µ and σ are the mean and standard deviation for we. we’ and we” are the standardized and discretized feature value, respectively. The obtained voxel value is denoted as W= (w1”, w2”, w3”), which is used as the observable vector in the following the potential vehicle voxels extraction processing. The above spatial structure assignment scheme is adopted here to meet the need of accurately separating vehicle bodies. Since integrating intensity, elevation and density information can reflect the physical and geometric characteristics of objects more comprehensively. The voxel value appears to be multi-valued, so the constructed structure is called a 3-D multi-valued voxel structure and is used as the source data for the subsequent vehicle recognition.
Extracting the potential vehicle voxels
The laser points belonging to the vehicle category should have similar density, intensity, and elevation value. The above consistency criterion is built up to extract the potential vehicle voxels. As shown in Fig. 1(a), the joint distribution of objects in the 2-D feature space of discretized elevation and intensity for the experimental data Area 1 is computed, in which the points in the 2D feature space correspond to the intensity and elevation values of all valuable voxels in the voxel structure.
As can be seen from Fig. 1(a), the statistical distribution of objects in the intensity and elevation feature space exhibits multimodality. The statistical distribution of objects in the density and elevation feature space also presents similar conclusions, as shown in Fig. 1(b). It can be inferred that the statistical distribution of objects in the 3-D feature space of density, intensity and elevation also shows multi-peaks. In order to fit the multimodal distribution and distinguish vehicle from non-vehicle objects, the multimodal distribution in 3-D feature space is regarded as the superposition of multi-dimensional Gaussian distribution, and multivariate GMM is introduced to model the multimodal distribution of objects in feature space. As a result, four individual trivariate normal distributions and theirs probability density function (pdf) are obtained and given by
where ρ12 (ρ13, ρ23) is the correlation coefficient of w1"and w2“(w1"and w3”, w2"and w3).
Given the voxel value of each valuable voxel, the probability of the voxel belong to each category can be respectively calculated according to Eq. (7), and thus obtain the membership matrix ujk, k is the index of trivariate normal distributions, k = 1, …, K. The class corresponding to the maximum membership value is judged as the category of a voxel. After that, the trivariate normal distribution corresponding to the vehicle can be identified according to the priori knowledge (the object(s) of each trivariate normal distribution can be seen from the top view of the constructed voxel structure and are used as prior knowledge, as shown in Fig. 5, and the voxels following this distribution are regarded as the potential vehicle voxel.
Separating the vehicle bodies
A vehicle body appears as a local continuous region and is discretized into a 3-D connected set in the constructed 3-D multivalued voxel structure, and thus can be separated by 3-D connected set construction. The 3-D connected set is obtained from a potential vehicle voxel by accumulating the set of other potential vehicle voxels connected to it. This may be achieved by recursively visiting a neighboring potential vehicle voxel and labeling the visited voxel with the vehicle label. The recursion terminates if there exists no unvisited neighboring potential vehicle voxel. This processing primarily employs the strategy of the depth first search for obtaining its connected component from a voxel. The above connected set construction result are related to the neighborhood size. The effects of neighborhood sizes on the vehicle bodies separation result and the optimal neighborhood size will be studied in the section Experimental Results and Discussions.
However, there may exist fake vehicle bodies in the above separation result because other objects exhibiting the similar intensity, density and elevation consistency as vehicles may mingled with them, so the separated 3-D connected sets are further verified and optimized according to the size characteristic of vehicles to obtain accurate vehicle bodies extraction result. The Minimum Area Bounding Rectangle (MABR, see Fig. 2) of each 3-D connected set is determined, if its size is within the limit of dimensions for motor vehicles (That is to say, the sizes of vehicles are in a certain range), the voxels within the corresponding MABR are identified and labeled as an individual vehicle. The limit of dimensions is determined according to “Limits of dimensions, axle load and masses for motor vehicles, trailers and combination vehicles” (GB1589-2016)25.
Except for the 3-D automatic extraction of vehicle bodies, attribute information of each vehicle body is further determined, containing the spatial location, type, size. The spatial location of each vehicle body is determined by the body center of its MABR. The size of each vehicle body is determined by the length, width, and height of its MABR. The vehicle type is determined according to size standards for all types of vehicles.
Evaluating the vehicle extraction accuracy
In order to compare the vehicle extraction result of the proposed algorithm to the Ground-truth data for vehicles, the discrete laser points included in the vehicle voxels are first extracted, then the extracted laser points and the Ground-truth data are compared point-by-point to provide a quantitative assessment by using the following accuracy metrics26.
\({\text{Type I error }}=\frac{{FN}}{{TP+FN}}\;{\text{Type II error }}=\frac{{FP}}{{FP+TN}}\;{\text{Total error }}=\frac{{FN+FP}}{{TP+FN+FP+TN}}\)
\({\text{Kappa }}=\frac{{{P_0} - {P_e}}}{{1 - {P_e}}}\;{P_0}=\frac{{TP+TN}}{{TP+FN+FP+TN}}\)
\({P_e}=\frac{{(TP+FN) \times (TP+FP)+(FP+TN) \times (FN+TN)}}{{{{\left( {TP+FN+FP+TN} \right)}^2}}}\)
where Type I error refers to the percentage of vehicle points rejected as non-vehicle points, Type II error refers to the percentage of non-vehicle points accepted as vehicle points, Total error refers to the percentage of incorrectly classified points, Completeness (CP) refers to the percentage of Ground-truth data being detected, Correctness (CR) refers to the percentage of correct extraction, Quality (Q) refers to the overall success rate, Kappa coefficient (KP) is a statistical measure of the inter-ratio agreement and is believed to be a more robust measurement than a simple percentage, TP (i.e. True Positive) denotes the number of vehicle points classified by both datasets, TN (i.e. True Negative) denotes the number of non-vehicle points classified by both datasets, FP (i.e. False Positive) denotes the number of vehicle points classified only by the proposed algorithm, FN (i.e. False Negative) denotes the number of vehicle points classified only by the Ground-truth data.
Description of experimental data
Two UAV-LiDAR point cloud datasets with different point densities are used for testing as follows.
-
(1)
Tianjin (China) Area 1. This experimental data are captured by the DJI Zenmuse L1 system of Da-Jiang Innovations Science and Technology Co. Ltd in 2022 with an average flying height of 100 m. The scene is acquired from a residential complex in Nankai District, Tianjin City, China. The study area is characterized by vehicles, roads, shrubs, vegetation, buildings and some other anomaly objects (e.g. irregular structures like pole or flowerbed). The testing point clouds (see Fig. 3(a), is denoted as Area 1) contain 21,030,435 laser points and have the average point density of 1379 points/m2. Ground-truth data for vehicles are manually extracted using Terrasolid software. 55 vehicles are included in Area (1) Information about the types of vehicles is presented in Table 1.
-
(2)
Dublin (Ireland) Area (2) This experimental data are provided by Urban Modelling Group at University College Dublin (UCD) and are available at https://v-sense.scss.tcd.ie/DublinCity/. The scene is acquired by a TopEye system S/N 443 in 2015 with an average flying height of 300 m and is acquired from the Dublin city centre. The testing point clouds (see Fig. 3(b)) are cut from T_316000_233500_NW.bin and is denoted as Area 2. Area 2 contains 6, 420, 653 laser points and has the average point density of 348 points/m2. Ground-truth data for vehicles are also provided in the previous website and can be used to quantitatively evaluate the accuracy of the proposed algorithm. There are 139 vehicles in Area 2. Information about the types of vehicles is presented in Table 1.
In the above two experimental datasets, most vehicles are parked along the street, some are parked around houses, and some under trees. The extraction of vehicles parking very close to each other and vehicles beneath tree represents the challenge of the proposed algorithm.
Experimental results and discussion
Parameter sensitivity analysis
Effect of different voxel sizes on the vehicle bodies separation accuracy is studied. Five typical schemes are tested. In the first one, (∆x1, ∆y1, ∆z1) are determined based on the average point spacing of the input UAV-LiDAR point clouds using Eq. (9).
where, λ is the average point density of the give point clouds data collection. In the second one, ∆x2 = ∆y2 = ∆z2 = 2 × ∆x1. By that analogy, ∆x3 = ∆y3 = ∆z3 = 3 × ∆x1, ∆x4 = ∆y4 = ∆z4 = 4 × ∆x1, ∆x5 = ∆y5 = ∆z5 = 5 × ∆x1.
Effect of different neighborhood sizes on the vehicle bodies separation accuracy is also simutaneously studied. 6 neighbors, 18 neighbors, 26 neighbors, and 56 neighbors are respectively applied to the multi-valued voxel structure with different voxel sizes under identical conditions. The separated vehicle voxels are compared to the vehicle truth data which are labeled manually using the Terrasolid software, and the corresponding error indexes are listed in Table 2. It is worth noting that the discrete laser point(s) included in the separated vehicle voxels are extracted to accomplish the accuracy evaluation.
As shown in Table 2, the voxel size of 0.01 m in combination with 26-connected set provide the minimum Total error for Area 1 and Area 2. Consequently, 0.01 m (4×∆x1) and 26 neighbors are recommended as the optimal voxel size and neighborhood size, respectively. The reasons for this may be that:
-
(1)
The idea behind the proposed algorithm is that voxels belonging to an individual vehicle can form a 3-D connected set with the vehicle sizes constraint. If the voxel size is too small, only vehicles with even sampling can form individual 3-D connected sets and can be correctly extracted. However, in practice, the point distribution of vehicles varies owing to occlusion or other reasons, data voids always exist in the low density region of vehicles. As a result, these vehicles will be partitioned into multiple 3-D connected sets (see Fig. 4(a)) and will be misclassified by the vehicle size constraint, thus giving rise to a big error (see the Total error for the voxel size of 0.025 m, 0.05 m, and 0.075 m in Table 2). In order to adapt to the uneven distribution of vehicle points, a bigger voxel size is required, see the 3-D connected set construction result in Fig. 4(b), the pink 3-D connected set reflects the geometry of the vehicle and are correctly classified to be vehicle according to the size constraint. With increasing of voxel size, on the other hand, if the voxel size is too big, several laser points representing different objects may be transformed into a single voxel, thus influencing the accuracy of vehicle extraction and giving rise to the big type II errors in Table 2. Simutaneously, non-vehicle (such as tree) and vehicle voxels may get connected, which also leads to the big Type II error.
-
(2)
Furthermore, even if the voxel size setting is optimal, voxels belonging to an individual vehicle also may be partitioned into multiple 3-D connected sets if the neighborhood size (such as 6 neighbors) is too small and could be removed according to the size constraint of a vehicle, and thus giving rise to the type I error, see the Type I error under 6 and 18 neighbors in Table 2. On the other hand, with an increase of neighborhood size, the probability of non-vehicle voxels being misclassified as vehicles increases, thus giving rise to an increase of Type II errors. This can explain why error increases when using 56 neighbors.
Experimental results
The original UAV-LiDAR point clouds are first voxelized into a 3-D multi-valued voxel structure with the recommended optimal voxel size of 0.1 m, as shown in Fig. 5, where the colors demonstrate RGB (R = density, G = elevation, B = intensity). By voxelization, 21,030,435 (6,484,134) laser points are remapped into a 3-D grid of size 1730 × 883 × 251 (2213 × 963 × 578), and 3,272,648 (242,532) non-zero voxels are obtained.
Based on the constructed 3-D multi-valued voxel structure, the potential vehicle voxels are extracted according to the intensity, elevation and density consistency of vehicles. The obtained potential vehicle voxels are depicted in Fig. 6.
The result in Fig. 6 demonstrates that the obtained potential vehicle voxels are mingled with many tree voxels. The reason for this is that the class of vehicle has small number of voxels compared to other majority classes and is overwhelmed by the majority class of tree. Therefore, the probability density distributions of vehicle and tree in the 3-D feature space of intensity, elevation and density form mixture of normal distribution. To discriminate between vehicle and tree voxels, the processing of 3-D connected set construction under size constraint is implemented among the potential vehicle voxels and as a result the vehicle bodies are separated. The corresponding result is visualized in Fig. 7.
As depicted in Fig. 7, the structure and shape of vehicles could be delineated in our vehicle bodies separation result, and the vehicle bodies representing using voxels can directly serve as the 3-D reconstruction model of vehicles with a certain accuracy.
By statistics, 109,340 (145,349) vehicle voxels are obtained, the inside laser points are extracted to compared to the vehicle truth data and thus evaluate the accuracy of the proposed algorithm quantitatively. The completeness, correctness, quality and Kappa coefficient of the proposed algorithm under the optimal voxel size and neighboring size are respectively 99.37% (98.29%), 99.83% (94.21%), 99.21% (93.95%), and 99.66% (93.95%). This means that: (1) The average quality and Kappa coefficient of the proposed algorithm is 96.58% (96.04%), respectively. (2) The higher the point density, the higher the vehicle extraction accuracy. The effectiveness of the proposed algorithm for separating vehicle bodies from high-denstiy UAV-LiDAR point clouds is verified.
By statistics, 55 (129) vehicle bodies are correctly extracted by the proposed algorithm for Area 1 (Area 2), particularly including several vehicles beneath trees and parking very close (see Fig. 8). This demonstrates that vehicle bodies can be extracted without being significantly affected by occlusion and the very close vehicle arrangement.
To analyse the factors affecting the completeness and correctness of the proposed algorithm, the top view of vehicle extraction results and the errors obtained using the proposed algorithm are shown in Fig. 9.
The vehicle recognition results in Fig. 10 demonstrate that the majority of the vehicle bodies (yellow points) are recognized correctly, especially for area 1, 55 vehicle bodies are all recognized. Thus, the proposed algorithm worked well for recognizing vehicles. The red points in Fig. 10 show that the major factor of incorrectness are as follows. Low shrubs that exhibit the similar intensity, elevation, density, and size characteristics as vehicles are misclassified as vehicles, resulting in a type II error. The blue points in Fig. 10 show that the major factors of incompleteness are as follows. Firstly, some vehicle points are missing seriously due to occlusion or other reasons, consequently, these vehicle bodies will form separate 3D connected sets and will be misclassified by the vehicle size constraint, thus giving rise to a type I error. Secondly, because of the different observing angle, lidar points corresponding to the side of the car are often incomplete (or even missing) and unevenly, and some laser points on the side of the car will also form separate 3D connected sets and will be misclassified.
Attribute information of the separated vehicle bodies are further determined. For an intuitive representation, the vehicle recognition result in Fig. 10 containing theirs index, size, type and spatial location information are represented in the Cartesian coordinate system.
Comparative algorithm performance
The performance of the propose algorithm is compared with that of the previous classic vehicle extraction algorithm18 in Table 3.
According to Table 3, when the point density is 300 points/m2 or even 1300 points/m2, the quality of the algorithm proposed by Zhang et al.18 is approximately 60%. However, according to Zhang et al.18, when the point density is 40 points/m2, the quality of the algorithm is approximately 70%. This indicates that the vehicle extraction algorithm designed based on high density point cloud cannot solve the problem of accurate vehicle recognition from super-high density UAV-LiDAR point clouds. Furthermore, the quality (Q) and Kappa of the proposed algorithm are both higher than the algorithm proposed by Zhang et al.18, improving the quality (Kappa) by about 37% (20%), respectively. The superiority of the proposed algorithm is proved.
Conclusions
To accurately recognize vehicles in complicated urban scenes, a new 3-D algorithm designed for the high-density UAV-LiDAR data is developed. The proposed algorithm first regularizes the original UAV-LiDAR point clouds into a multi-valued voxel structure, in which the voxel value denotes the discretized mean intensity, elevation, and density value of inside laser point(s). Then, the potential vehicle voxels are extracted according to the intensity, elevation, and density consistency of vehicle voxels. Subsequently, vehicle bodies are separated by the idea of 3-D connected set construction under size constraint. At last, the quantified attribute information of the vehicle bodies are determined. The advantages of the proposed algorithm lies in that: It is designed based upon a multi-valued voxel structure and can directly realize the 3-D automatic extraction, visualization and structuring of vehicles. It comprehensively utilizes of the intensity and geometric information of vehicles and provides a new feasible and effective solution for vehicle recognition. The experimental results demonstrate that the proposed algorithm can be effectively utilized for comprehensive and accurate recognition of vehicles and is robust to occlusion. The average quality (Kappa coefficient) of vehicle extraction can reach to 96.58% (96.04%). However, due to different observation angles, vehicle laser points are unevenly distributed, most of the UAV-LiDAR points distribute on the top of the vehicle. The uneven point density distribution may affect the accuracy of vehicle extraction. This is also the limitation of the proposed algorithm although it does not affect the overall geometry of the extracted vehicles. In the future, data filling or multi-source data fusion methods might be developed to improve the completeness of the extracted vehicles, which would make this algorithm more efficient and robust.
Data availability
The datasets used during the current study available from the corresponding author on reasonable request.
References
Toth, C. K., Barsi, A. & Lovas, T. Vehicle recognition from LiDAR data. Int. Arch. Photogramm Remote Sens. 34, W13 (2003).
Wen, N., Wang, X., Guo, J., Wang, Y. & Wang, Y. Multi-modal fusion of LiDAR and camera sensors for enhanced perception in intelligent traffic systems. Int. Conf. Electron. Eng. Inf. Syst. (EEISS) 10, 166–174 (IEEE).
Yao, W. & Wu, J. Airborne LiDAR for Detection and Characterization of Urban Objects and Traffic Dynamics 367–400 (Urban Informatics, 2021).
Shobha, B. S. & Deepu, R. A review on video based vehicle detection. Recognit. Track. 12, 20–22 (2018).
Lin, H. et al. A deep learning framework for video-based vehicle counting. Front. Phys. 10, 829734 (2022).
Eikvil, L., Aurdal, L. & Koren, H. Classification-based vehicle detection in high-resolution satellite images. ISPRS J. Photogramm Remote Sens. 64, 65–72 (2009).
Wang, Y., Peng, F., Lu, M. & Asif Ikbal, M. Information extraction of the vehicle from high-resolution remote sensing image based on convolution neural network. Recent. Adv. Electr. Electron. Eng. (Formerly Recent. Pat. Electr. Electron. Engineering). 16, 168–177 (2023).
Barsi, Á. R. T. L. Á. LiDAR-based vehicle segmentation. Remote Sensing 115,156–159 (2004).
Yao, W., Hinz, S. & Stilla, U. Automatic vehicle extraction from airborne LiDAR data of urban areas aided by geodesic morphology. Pattern Recognit. Lett. 31, 1100–1108 (2010).
Yao, W., Hinz, S. & Stilla U.3D object-based classification for vehicle extraction from airborne LiDAR data by combining point shape information with spatial edge 10,1–4 (IEEE)(2010).
Börcs, A. & Benedek, C. Extraction of vehicle groups in airborne LiDAR point clouds with two-level point processes. IEEE Trans. Geosci. Remote Sens. 53, 1475–1489 (2014).
Bowman, L. A., Narayanan, R. M., Kane, T. J., Bradley, E. S. & Baran, M. S. Vehicle detection and attribution from a multi-sensor dataset using a rule-based approach combined with data fusion. Sensors. 23, 8811 (2023).
Yao, W., Hinz, S. & Stilla, U. Extraction and motion estimation of vehicles in single-pass airborne LiDAR data towards urban traffic analysis. ISPRS J. Photogramm Remote Sens. 66, 260–271 (2011).
Liu, Z. & Li, C. W. Vehicle extraction method based on decision level data fusion of airborne LiDAR point cloud. Geospatial Inf. 20, 128–132 (2022).
Qi, Y. et al. Geometric information constraint 3D object detection from LiDAR point cloud for autonomous vehicles under adverse weather. Transp. Res. Part. C Emerg. Technol. 161, 104555 (2024).
Lin, C., Wang, Y., Gong, B. & Liu, H. Vehicle detection and tracking using low-channel roadside LiDAR. Measurement. 218, 113159 (2023).
Toth, C. K., Grejner-Brzezinska, A. & Moafipoor, S. D. Precise vehicle topology and road surface modeling derived from airborne LiDAR data. Proc. 60th Annu. Meet. Inst. Navig. 6, 401–408 (2004).
Zhang, J., Duan, M., Yan, Q. & Lin, X. Automatic vehicle extraction from airborne LiDAR data using an object-based point cloud analysis method. Remote Sens. 6, 8405–8423 (2014).
Eum, J. et al. Vehicle detection from airborne LiDAR point clouds based on a decision tree algorithm with horizontal and vertical features. Remote Sens. Lett. 8, 409–418 (2017).
Zhang, T., Kan, Y., Jia, H., Deng, C. & Xing, T. Urban vehicle extraction from aerial laser scanning point cloud data. Int. J. Remote Sens. 41, 6664–6697 (2020).
Y, K. Urban Basic Information Extraction Based on Airborne LiDAR Point Cloud (Southwest Jiaotong University, 2021).
Kuželka, K. & Slavík, M. Surový P.Very high density point clouds from UAV laser scanning for automatic tree stem detection and direct diameter measurement. Remote Sens. 12, 1236 (2020).
Yan, W. Y. & Shaker, A. Radiometric correction and normalization of airborne LiDAR intensity data for improving land-cover classification. IEEE Trans. Geosci. Remote Sens. 52, 7658–7673 (2014).
Li, C. & Xu, Z. Structure Identification-based clustering according to density consistency. Math. Probl. Eng. 890901 (2011). (2011).
GB 1589–2016. Limits of Dimensions, axle load and Masses for Motor Vehicles (trailers and combination vehicles, 2016).
Wang, L., Xu, Y., Li, Y. & Zhao, Y. Voxel segmentation-based 3D building detection algorithm for airborne LIDAR data. Plos One. 13, e0208996 (2018).
Acknowledgements
The work was supported by the National Natural Science Foundation of China (Grant No. 42201482), GPU resource support project of Liaoning Technical University.
Author information
Authors and Affiliations
Contributions
Liying Wang: Conceptualization; Methodology; Writing - Review & Editing; Supervision; Funding acquisition. Huaxin Chen: Writing - Original Draft; Validation. Ze You: Data Curation Investigation; Visualization.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, L., Chen, H. & You, Z. Combining geometrical and intensity information to recognize vehicles from super-high density UAV-LiDAR point clouds. Sci Rep 14, 25097 (2024). https://doi.org/10.1038/s41598-024-75968-z
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-024-75968-z