Introduction

With the continuous advancement of China’s power market-oriented reform, it is gradually developing towards the establishment of a market with unified, open, orderly1. And the market-oriented transaction involving renewable energy is also developing towards parity. Based on the current situation of energy and load distribution in China, cross-regional consumption has become an important technology to improve the utilization rate of renewable energy, crack the development of renewable energy and achieve the emission reduction target. However, due to the lack of in-depth research on the factors affecting the consumption of cross-regional transactions, the problems of wind and PV curtailment are prominent. It is seriously puzzling the development of China’s power market. So, in the early stage of marketization reform, the market awareness of participants is weak, it is impossible to ensure that renewable energy can participate in the market-oriented transactions without a mandatory transaction mechanism.

To solve the problems, learn from the advanced experience of many countries that the green certificate program (GCP) is considered to be an excellent institutional innovation to effectively promote the healthy development of renewable energy2. In recent years, as the global effort toward carbon neutrality intensifies, green certificate markets have emerged as a critical mechanism to promote renewable energy development. Green certificates, also known as Renewable Energy Certificates, represent proof that a certain0 amount of renewable electricity has been generated and can be traded to demonstrate compliance with renewable energy consumption or quota obligations. Through market-based mechanisms, green certificates aim to provide additional revenue streams for renewable energy generators while encouraging end-users, corporations, and local governments to meet renewable energy consumption targets. GCP has achieved good results in many countries2: based on the implementation effect in five major European countries in the past 10 years (2000–2010), and concluded that the GCP can promote the development of renewable energy in the short and long term3. Believed that GCP will help to achieve Spain’s renewable energy development goal in 20204. Analyzed the results of short-term and long-term implementation of GCP in Denmark under autarky and external trade, and decompose the causes of the increase in green power capacity and consumption of domestic.

Current policy framework

China, as the world’s largest renewable energy market, has gradually advanced the development of its green certificate trading system in recent years. China’s green certificate market was officially launched in 2017, when the National Development and Reform Commission and the National Energy Administration introduced the "Green Power Certificate Issuance and Voluntary Trading Mechanism." This voluntary scheme allowed renewable energy generators to apply for green certificates, which could then be traded in the market and sold to enterprises and individuals interested in supporting green energy development. However, the early voluntary trading mechanism did not achieve significant results, with limited market participants and relatively low transaction volumes.

In 2019, China introduced a mandatory quota system to further incentivize renewable energy deployment. This system requires local grid companies and certain large users to either purchase green certificates or directly use renewable energy to fulfill their renewable energy quota obligations. The quota system injected new vitality into the green certificate market, adding regulatory strength to ensure the market’s growth. However, uncertainties in the policy’s execution, especially in balancing the interests of local governments, power generators, and end-users, continue to challenge the system’s full potential.

Market size

Compared with the relatively mature transaction market of GCP, China is still in the initial stage, the mandatory has not been implemented. Combined with the implementation experience of foreign, many scholars put forward policy suggestions for the construction and implementation of GCP in China5. Divided GCP into two stages: limited transaction and free transaction, and put forward the operation mode of each stage6. Point out the planning and layout need to be formulated in GCP to prevent the blind investment of renewable energy manufacturers7. Analyzed the economic impact of GCP and believes it can replace government concession bidding and tax subsidies, to alleviate the plight of the increasing shortage of funds8. Use the Stackelberg game model to simulate the behavior of participants, and formulated price and penalty in GCP9. Studied the impact of GCP on the development of China’s renewable energy industry and energy structure from the circular structure, dynamic characteristics, and optimal economic model, the result shows that GCP can effectively promote the sustainable development of China’s wind power industry10. Put forward policy suggestions on subsidies and punishment for the periodic decline, which will help to promote the scale of GCP. With the efforts improvement of GCP, according to the data of the green certificate subscription platform in China, there are 3794 subscribers from July 1, 2017, to November 2021. The subscribers are all power enterprises and individuals, and a total of 101869 green certificates have been subscribed. Despite China’s vast renewable energy capacity, the scale of the green certificate market remains relatively small. According to data from the National Energy Administration, while the issuance of green certificates has steadily increased year by year, the market penetration of green certificates remains low compared to the country’s total renewable energy output. The voluntary trading market has seen limited activity due to high price volatility and low awareness among consumers regarding the benefits of purchasing green certificates. As of 2023, the majority of green certificate transactions in China have been conducted between large enterprises and local grid companies, with the market yet to expand significantly to medium-sized enterprises and individual end-users. Recent statistics show considerable fluctuations in green certificate prices, largely due to imbalances between supply and demand. The maturity of the green certificate market remains underdeveloped compared to the overall progress in renewable energy deployment, necessitating further optimization of market mechanisms.

At present, most renewable energy plants are registered, but the distribution companies fail to respond. As a result, the competition among green power plants is huge, and the demand cannot be dynamically balanced. Furthermore, the transaction of green certificates is very low, and the profits from GCP can not replace government subsidies for green power plants.

Trading model

Participants in the bilateral transaction can determine the price and electricity of transactions through free negotiation11. Through advanced experience abroad, the bilateral transaction can hedge price risk and get free competition. So it is an excellent manner to fully mobilize more subjects to participate12. Believed that bilateral transactions can hedge the uncertainty of price and quantity in the day-ahead auction in the power market13. Proposed a new type of bilateral transaction for the distribution system to efficiently incentivize the demand-side14. Redistribute the interests among participants in GCP by the bilateral transaction to guide mutually beneficial cooperation. Based on the above research, bilateral transactions have reference significance for the development of GCP in China. Furthermore, China has announced that GCP will be enforced from 202115, which will promote the circulation of green certificates and induce participants to adopt strategic behavior to obtain more returns. However, the implementation of compulsory will greatly increase the number of participants. Due to the heterogeneity of participants, the transaction behavior is complex, and some scholars have conducted relevant research. The agent-based modeling is embedded into GCP in15 to study the strategic behavior of each participant16. Considered the preference of obligation subject in GCP, and analyzes the optimal transaction strategy between cross-provincial transactions17. Combined the energy market with the green certificates market to build an equilibrium model for day-ahead/real-time, to study the strategic behavior of participants under different markets. Based on the above analysis, participants in bilateral transactions of green certificates are numerous, and all are decision-makers. So the strategic behavior of each should consider not only itself but also the influence of others. Engineering game theory18 fully considers the flexible interaction between participants, which is one of the best manners to analyze their complex conflicts of interest19. Studied the transaction price of GCP from the investment decisions based on the two-stage game model20. Used the cooperative game, bargaining game, and alliance game to explore the strategic behavior of each participant. Although the above studies have analyzed the implementation effect and strategic behavior in GCP, they have less consideration on the safe operation of the power grid and technical characteristics of generation units. It makes the transaction plan squeezes the real schedulable space and seriously endangers the safe operation of the system. Furthermore, the transaction plan is reduced due to it not meeting the security constraints21, which loses fairness22 for the participants.

Uncertainty of power generation

In addition, multiple generation uncertainty is still the main challenge for green certificate transactions to be continuous and reliable. Distributed robust optimization (DRO) combines the advantages of stochastic optimization and robust optimization and takes into account the randomness of parameters in the probability distribution of uncertain variables. DRO is applied to the power system for the first time in23 to analyze the uncertainty of wind power and solve the cooperative operation of the hydro-thermal-wind system. At present, DRO has been widely used in the fields of unit commitment, optimal power flow calculation, operation planning for multi-energy coupling systems, and so on24. Described the uncertainty of wind power output by DRO, and proposed a unit commitment optimization model. A day-ahead scheduling model of the park-level integrated energy system is proposed based on DRO in25, and a chance-constrained and interval optimization for integrated electricity and natural gas systems optimal power flow is proposed based on DRO in26. Considering the uncertainty of electricity price, waste supply, and central heating demand27, studied the transaction strategies for waste-to-energy plants based on DRO28. Proposed a decentralized management model for wind power based on DRO, which can effectively deal with high-dimensional uncertainty and improve reliability without sacrificing the operation cost. A dynamic optimal power flow model of the wind-PV-hydro-thermal system based on DRO is proposed in29 to coordinate the economy and robustness. A coordinated optimization model of power to gas is proposed in30 based on DRO to stabilize the fluctuation of wind power through multi-energy interaction. In the application of DRO, it is the key to constructing the fuzzy set of the probability distribution for the uncertain variables. At present, most manners are based on Wasserstein distance, KL divergence, multi discrete scene, and moment information. The classification and summary of some existing research are shown in Table 1.

Table 1 The comparison of construction methods for fuzzy set in DRO.
Full size table

In summary, the key in the application of DRO is to select an appropriate method to construct the fuzzy set of the probability distribution. When the radius of the Wasserstein sphere and the number of scenes cannot be accurately determined, the accuracy of the transaction plan or scheduling scheme also needs to be discussed. Furthermore, the above research mainly focuses on the characterization of uncertain variables under a single time section, but the uncertainty of generation power correlates among multiple periods.

Key challenges

Despite the positive progress made, the green certificate market in China faces several policy, market, and regulatory challenges:

Policy Stability and Consistency: While the government has introduced various policies to support green certificate trading, the stability and consistency of these policies remain a concern. Inconsistent execution across different regions creates uncertainty for market participants, limiting the long-term development of the market. Participants often lack clear expectations for the future direction of policies, which hinders their willingness to engage actively in the market.

Supply-Demand Imbalance: The imbalance between the supply and demand of green certificates remains a persistent issue. Some regions, rich in renewable energy resources, experience an oversupply of green certificates, while other regions struggle with insufficient supply. This imbalance exacerbates price volatility and undermines the overall effectiveness of the market.

Low Market Participation: Currently, the primary participants in China’s green certificate market are local grid companies, large enterprises, and certain government departments. Participation from small and medium-sized enterprises and individual consumers remains low. This lack of diverse market participants not only limits the scale of the market but also reduces the competitive dynamics and vibrancy of the trading environment.

Market Manipulation and Unfair Competition: As the market expands, issues related to market manipulation and unfair competition have started to emerge. Certain participants may attempt to manipulate certificate prices or hoard certificates for speculative purposes, which calls for stronger regulatory oversight to ensure a fair and transparent market.

Complex Stakeholder Dynamics: The green certificate market involves a complex interplay of interests among renewable energy generators, local governments, and end-users. Under the mandatory quota system, these stakeholders have differing priorities and objectives. Balancing these competing interests while ensuring fair and effective market operation is a major challenge that requires careful policy design and execution.

Power Generation Uncertainty: One of the inherent challenges of the green certificate market is the uncertainty in renewable power generation. Wind and solar energy generation are subject to significant variability due to weather conditions and other environmental factors. This variability makes it difficult to predict the exact amount of renewable energy that can be produced over a given period, which in turn impacts the number of green certificates available for trading. The unpredictability in generation complicates planning for both energy producers and certificate purchasers, leading to potential mismatches between supply and demand and further contributing to price volatility in the market.

Based on the above analysis, a cross-regional bilateral transaction model of GCP considering the technical characteristics of generation units is proposed to solve the problems such as the mismatch between supply and demand of green certificates and the reduction of transaction plan constrained by power grid operation. This model aims to balance the interests of different participants by optimizing the market mechanism, prevent market manipulation, and provide a theoretical basis and policy recommendations for the healthy development of the green certificate market in the future.

The main contributions are as follows:

  1. (1)

    In the cross-regional bilateral transaction of GCP, to mobilize the initiative of more participants and improve the enforceability and fairness of the transaction plan, a transaction model for multi-participant is proposed. In the model, the bilateral transaction is used to improve the degree of free competition, and the constraints of units and the grid are considered to improve the enforceability of the transaction plan. Linking green power generation enterprises with traditional fossil energy power generation enterprises, and bringing additional benefits to different market participants through global optimization and configuration of TGC, to stimulate renewable energy power generation and limit the carbon emissions of traditional fossil energy units, can promote the dynamic change of China’s energy structure and promote energy transformation.

  2. (2)

    In the bilateral transaction of GCP, to improve the reliability of transaction plans under generation uncertainty, a distributed robust uncertainty description method based on Bayesian theory is proposed. Among them, the Bayesian multivariate nonlinear model and mixed-effect model are proposed to construct the fuzzy sets for the probability distribution of wind and PV output. This method can deal with the defect of DRO that the fuzzy set is subjective and only for analysis in a single time section.

  3. (3)

    In the bilateral transaction of GCP, to take into account the economy and conservatism of transaction plan in extreme cases of power generation deviation, the spatial constraint parameters are used to adjust the uncertain set boundary, are the probability values outside extreme cases are used to quantify the robustness, and then to balance the economy and conservatism scientifically.

  4. (4)

    In the bilateral transaction of GCP, to prevent improper cooperation and competition to manipulate the market and maliciously rising electricity prices, the strategic game model of multi-participant is constructed and the complex interest and strategic behavior of multi-participant are analyzed. The Nash equilibrium results under various game modes are compared and explore the sensitivity of equilibrium results to uncertainty factors.

The strategic game model of multi participants under cross-regional green certificate bilateral transaction

Structure and operation mode of cross-regional green certificate bilateral transaction model

model structure

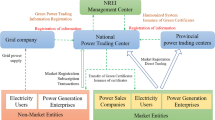
The model structure is shown in Fig. 1. The region where the obligation subject is located is the receiving end region, which is the region with a large number of loads. The main power supply mode is thermal power generation, and there is no large-scale renewable energy; In this mode, green power plants in other regions, while meeting the transmission constraints of the tie-line through cross-regional transactions, transmit the purchased power to the obligation subject through the tie-line. The obligation subject receives the power through the tie-line and adjusts the thermal power output strategy in this region, so that the power grid in this region can operate stably.

Fig. 1
figure 1

Model structure.

Full size image

Transaction operation mode

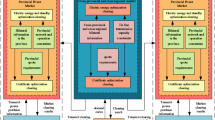
The many-to-many automated negotiation protocol in the green certificate bilateral transaction is more in line with the development needs of the future power market in China. The transaction process is shown in Fig. 2.

Fig. 2
figure 2

Many-to-many automated negotiation protocol in the green certificate bilateral transaction.

Full size image

The subjects in Fig. 2 are green power plants and obligation subjects. Green power plants include wind power, photovoltaic, hydropower, and other renewable energy power plants. Obligation subjects are the provincial power grid enterprises divided according to the assessment tasks. To improve revenue, green power plants will increase the transaction price and efforts to develop more renewable energy. In this case, it will accelerate the transformation of energy structure on the power side. Based on completing the quota task, the obligation subjects will reduce the transaction price of the green certificate to ensure its profit.

The competitiveness of green certificate bilateral transactions is mainly reflected in the difference between pricing and quantification and will make them have great uncertainty and then increase the business risk. To avoid that, multiple subjects will ally to maximize their interests. Superior green power plants with more accurate prediction ability and large power generation have greater pricing power, and inferior plants with limited and have less pricing power. To ensure revenue, inferior plants often cooperate with superior plants to improve the adverse situation. Obligation subjects with the large demand for green certificates and intensive load have greater quantitative rights in transactions and are in a strong position, the subjects in a weak position also need to cooperate with them. Furthermore, to ensure the consumption of renewable energy power, the balance of supply and demand, and the completion of policy indicators, there are also cooperative between green power plants and obligation subjects. Therefore, multiple alliances will be formed, which can be divided into:

  1. (1)

    For inferior green power plants, they always hope to join the alliance of superior plants to improve their transaction price and opportunities.

  2. (2)

    For the obligation subjects in a weak position always hope to cooperate with the subjects in a strong position to reduce the transaction price of the green certificate.

  3. (3)

    For the obligation subjects always hope to cooperate with the green power plants, to ensure the effective supply of green certificates. Avoid the price risk caused by the decline in the number of green certificates in several months.

  4. (4)

    For the green power plants always hope to cooperate with the obligation subjects, to ensure profits through the green certificate transaction and avoid the risk of excessive competition among green power plants.

The basic elements of cooperative game

  1. (1)

    Player

    The basic elements of the cooperative game include player, strategy, and payment. Based on Section "The strategic game model of multi participants under cross-regional green certificate bilateral transaction", this section models the strategic behavior of one obligation subject and two green power plants. The 3 players are represented by OS, GPA, and GPB respectively, and the set of players is recorded as N = {OS, GPA, GPB}.

  2. (2)

    Strategy

    The strategies of the OS are the green certificate demand from GPA/GPB, which are recorded as \(Q_{OS,GPA}^{TGC} ,\;Q_{OS,GPB}^{TGC}\). Furthermore, to ensure the balance and stability of supply and demand, thermal units are configured as a necessary supplement. The output of thermal units \(P_{i,t}^{G}\) is affected by the green certificate demand, so they are also the strategy of OS. The strategies of GPA and GPB are the transaction prices, which are recorded as \(C_{GPA,OS}^{TGC} ,\;C_{GPB,OS}^{TGC}\).

    The above strategies are taken continuously in a certain interval, regardless of the impact of the dead zone for power units. So the OS and GPA/GPB have continuous strategic space. The collection of strategy is recorded as \(\Omega = \left( {\Omega_{OS} ,\;\Omega_{GPA} ,\;\Omega_{GPB} } \right)\) and recorded respectively as \(C_{GPA,OS}^{TGC} \in \Omega_{GPA} = \left[ {C_{GPA,\min }^{TGC} ,C_{GPA,\max }^{TGC} } \right],\;C_{GPB,OS}^{TGC} \in \Omega_{GPB} = \left[ {C_{GPB,\min }^{TGC} ,C_{GPB,\max }^{TGC} } \right]\), \(Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ;P_{i,t}^{G} \in \Omega_{OS} = \left[ {Q_{OS,\min }^{TGC} ,Q_{OS,\max }^{TGC} ,P_{i,\min }^{G} ,P_{i,\max }^{G} } \right]\). Where, \(C_{GPA,\min }^{TGC} /C_{GPA,\max }^{TGC} //C_{GPB,\min }^{TGC} /C_{GPB,\max }^{TGC}\) are the limits price of GPA and GPB, \(Q_{OS,\min }^{TGC} /Q_{OS,\max }^{TGC}\) are the limits demand of green certificate, \(P_{i,\min }^{G}\)/\(P_{i,\max }^{G}\) are the limit output of thermal units.

  3. (3)

    Payment

    This paper studies the day-ahead power transaction plan and designs the payment function of each player in the total cycle of 24 h. The payment is defined as the player’s income during the total transaction cycle and recorded as \(I_{OS} /I_{GPA} /I_{GPB}\), so the payment vector of the cooperative game is \(I = \left( {I_{OS} ,I_{GPA} ,I_{GPB} } \right)\).

  4. (4)

    Equilibrium

    Based on the above elements of the game, the Nash equilibrium can be obtained (if they exist), which are recorded as \(C_{GPA,OS}^{TGC*} /C_{GPB,OS}^{TGC*} /Q_{OS,GPA}^{TGC*} /Q_{OS,GPB}^{TGC*} /P_{i,t}^{G*}\).

The payment of each player

The obligation subject

The revenue of the obligation subject mainly comes from the power sales, and the cost mainly includes the power purchase, green certificate purchase, and penalty, as shown in (1).

$$\begin{gathered} I_{OS} = \sum\limits_{t = 1}^{T} {\left( \begin{gathered} C_{OS}^{SELL} \times D_{OS,t} \times 95\% - C_{t}^{G} - C_{OS}^{grid\_re} \times \sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} - } \hfill \\ \sum\limits_{{n \in \left( {GPA,GPB} \right)}} {\left( {C_{n,OS,t}^{TGC} \times Q_{OS,n,t}^{TGC} } \right) - \omega \psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right)} \hfill \\ \end{gathered} \right)} - \hfill \\ C_{OS}^{P} \times \max \left\{ {\left( {\sum\limits_{t = 1}^{T} {\left( {D_{OS,t} \times 95\% \times \alpha_{OS} } \right) - \sum\limits_{t = 1}^{T} {\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } } } } \right),0} \right\} \hfill \\ \end{gathered}$$
(1)

In Eq. (1) the first item is the power sales revenue, which comes from 95% of the load. The second item is the generation cost of thermal units, which is approximated as the fuel cost, as follow:

$$C_{t}^{G} = \sum\limits_{i = 1}^{{N^{G} }} {\left\{ {a_{i}^{G} + b_{i}^{G} P_{i,t}^{G} + c_{i}^{G} \left( {P_{i,t}^{G} } \right)^{2} + \left| {d_{i}^{G} \sin \left[ {e_{i}^{G} \left( {P_{i,\min }^{G} - P_{i,t}^{G} } \right)} \right]} \right|} \right\}}$$
(2)

The third item is the purchase cost of renewable energy, the fourth is the purchase cost of green certificates, and the fifth is the penalty cost for incomplete quota. To distinguish different obligation subjects, the "ability of quota completion" function \(\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right)\) is introduced in the sixth item. \(\omega\) is the weight factor, which indicates the ability of quota completion of all obligation subjects. \(\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right)\) is the relationship between transaction electricity and the total quota, which can be expressed in (3) by the dissatisfaction function.

$$\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right) = - \beta_{OS} \times \left( {D_{OS,t} \times 95\% \times \alpha_{OS} } \right) \times {\rm I}n\left[ {\sin \left( {\frac{{\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } }}{{D_{OS,t} \times 95\% \times \alpha_{OS} }}} \right) / \sin \left( { - 1 + \frac{\pi }{2}} \right)} \right],\beta_{OS} > 0$$
(3)

Where, \(\beta_{OS}\) is the priority parameters of OS, the bigger the more priority in the transaction. From (3), \(\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right)\) is a continuously decreasing concave function of \(\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} }\). When \(\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } < \left( {D_{OS,t} \times 95\% \times \alpha_{OS} } \right),\;\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right) > 0\), it indicates that OS cannot complete the quota. When \(\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } > \left( {D_{OS,t} \times 95\% \times \alpha_{OS} } \right),\;\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right) < 0\), it indicates that the quota can be completed. With the \(\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} }\) increase, the ability of quota completion reaches saturation gradually, and the \(\psi \left( {Q_{OS,GPA,t}^{TGC} ,Q_{OS,GPB,t}^{TGC} } \right)\) changes more and more slowly.

The OS also needs to consider the operation of thermal units, including output and climbing constraints, as follows:

$$\left\{ \begin{gathered} P_{i,\min }^{G} \le P_{i,t}^{G} \le P_{i,\max }^{G} \hfill \\ D_{i,t}^{G} \le P_{i,t}^{G} - P_{i,t - 1}^{G} \le U_{i,t}^{G} \hfill \\ \end{gathered} \right.,\forall i,t$$
(4)

The daily quota task constraint:

$${\raise0.7ex\hbox{${\sum\limits_{t = 1}^{T} {\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } } }$} \!\mathord{\left/ {\vphantom {{\sum\limits_{t = 1}^{T} {\sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } } } {\sum\limits_{t = 1}^{T} {\left( {D_{OS,t} \times 95\% } \right)} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sum\limits_{t = 1}^{T} {\left( {D_{OS,t} \times 95\% } \right)} }$}} \ge \alpha_{OS}$$
(5)

And the constraint of power supply and demand balance:

$$\sum\limits_{i = 1}^{{N^{G} }} {P_{i,t}^{G} } + \sum\limits_{{n \in \left( {GPA,GPB} \right)}} {Q_{OS,n,t}^{TGC} } - \left( {D_{OS,t} \times 95\% } \right) = 0$$
(6)

The green power plant

The payment functions of GPA/GPB are similar, take GPA as an example. And assumed that there is no obstacle to consumption, that is the government will recover the remaining at a lower price when the supply of green certificates is excessive. The revenue of GPA includes the income from selling power and green certificates and recycling by the government. The cost includes power generation. As shown in (7).

$$I_{GPA} = \sum\limits_{t = 1}^{T} {\left( \begin{gathered} C_{OS}^{grid\_re} \times q_{GPA,t} + C_{GPA,OS,t}^{TGC} \times Q_{OS,GPA,t}^{TGC} + C^{rec} \times \max \left\{ {0,q_{GPA,t} - Q_{OS,GPA,t}^{TGC} } \right\} \\ - C^{g} \times q_{GPA,t} - \omega^{\prime } \gamma \left( {Q_{OS,GPA,t}^{TGC} } \right) \\ \end{gathered} \right)}$$
(7)

Where, \(q_{GPA,t}\) is the generation plan of GPA at t, which is related to the wind speed, solar radiation intensity, and temperature in the area. To distinguish different green power plants, the "ability of generation" \(\gamma \left( {Q_{OS,GPA,t}^{TGC} } \right)\) is introduced in the fifth item. \(\omega^{\prime }\) is the weight factor, which indicates the ability of generation of all green power plants. \(\gamma \left( {Q_{OS,GPA,t}^{TGC} } \right)\) is the relationship between \(Q_{OS,GPA,t}^{TGC}\) and \(q_{GPA,t}\), which can be expressed in (8) by the dissatisfaction function.

$$\gamma \left( {Q_{OS,GPA,t}^{TGC} } \right) = - \beta_{GPA} \times q_{GPA,t} \times \ln \left[ {\sin \left( {\frac{{Q_{OS,GPA,t}^{TGC} }}{{q_{GPA,t} }}} \right) / \sin \left( { - 1 + \frac{\pi }{2}} \right)} \right],\beta_{GPA} > 0$$
(8)

Where, \(\beta_{GPA}\) is the priority parameters of GPA, the bigger the more priority in the transaction. From (8), \(\gamma \left( {Q_{OS,GPA,t}^{TGC} } \right)\) decreases with the increase of \(Q_{OS,GPA,t}^{TGC}\), and always greater than 0.

The transaction electricity of GPA at t is less than the power generation plan, with the constraints as follows:

$$Q_{OS,GPA,t}^{TGC} \le q_{GPA,t} ,\forall t$$
(9)

Tie line constraints are as follows:

Tie line transmission direction constraint

$$Q_{OS,GPA,t}^{TGC} \ge 0,\forall t$$
(10)

Lower and upper limits of tie-line power

$$P_{L}^{dc} \le Q_{OS,GPA,t}^{TGC} \le P_{F}^{dc} ,\forall t$$
(11)

Tie-line power climbing rate constraint

$$P_{down}^{dc} \le Q_{OS,GPA,t}^{TGC} - Q_{OS,GPA,t - 1}^{TGC} \le P_{up}^{dc} ,\forall t$$
(12)

The strategic game model with multi-player

This section establishes different game models by applying engineering game theory. By bringing in real data, it simulates the decision-making interaction process among three subjects and analyzes the strategic choices of the subjects in different cooperation models. Then, by enumerating all the potential cooperation models and analyzing the benefits and stability of different cooperation models, an optimal and most stable cooperation model is derived. Specifically, the game model helps to identify the optimal strategy combinations of different subjects in cooperation, and a stable cooperation model is derived through multiple iterative solutions, which directly reflects the practical application value of game theory in the field of electric power trading. There are 5 strategic modes for the green certificate bilateral transactions of OS and GPA/GPB, in Table 2.

Table 2 Strategic game model of multi-player in the bilateral transaction of green certification.
Full size table

The Nash equilibrium in the non-cooperation should meet the following relations:

$$\left\{ \begin{gathered} \left\{ {Q_{OS,GPA}^{TGC * } ,Q_{OS,GPB}^{TGC * } ,P_{i,t}^{G * } } \right\} = I_{OS} \left( {Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ,P_{i,t}^{G} ,C_{GPA,OS}^{TGC * } ,C_{GPB,OS}^{TGC * } } \right) \\ \left\{ {C_{GPA,OS}^{TGC * } } \right\} = I_{GPA} \left( {Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ,P_{i,t}^{G} ,C_{GPA,OS}^{TGC * } ,C_{GPB,OS}^{TGC * } } \right) \\ \left\{ {C_{GPB,OS}^{TGC * } } \right\} = I_{GPB} \left( {Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ,P_{i,t}^{G} ,C_{GPA,OS}^{TGC * } ,C_{GPB,OS}^{TGC * } } \right) \\ \end{gathered} \right.$$
(13)

where \(\left\{ {Q_{OS,GPA}^{TGC * } ,Q_{OS,GPB}^{TGC * } ,P_{i,t}^{G * } } \right\}/C_{GPA,OS}^{TGC * } /C_{GPB,OS}^{TGC * }\) are their optimal decisions under the optimal of others.

Taking {OS}, {GPA, GPB} as an example, the other situations are similar. The Nash equilibrium under the partial cooperative mode should meet the following relationship:

$$\left\{ \begin{gathered} \left\{ {Q_{OS,GPA}^{TGC * * } ,Q_{OS,GPB}^{TGC * * } ,P_{i,t}^{G * * } } \right\} = I_{OS} \left( {Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ,P_{i,t}^{G} ,C_{GPA,OS}^{TGC * * } ,C_{GPB,OS}^{TGC * * } } \right) \\ \left\{ {C_{GPA,OS}^{TGC * * } ,C_{GPB,OS}^{TGC * * } } \right\} = I_{GPA,GPB} \left( {Q_{OS,GPA}^{TGC * * } ,Q_{OS,GPB}^{TGC * * } ,P_{i,t}^{G * * } ,C_{GPA,OS}^{TGC} ,C_{GPB,OS}^{TGC * } } \right) \\ \end{gathered} \right.$$
(14)

where \(I_{GPA,GPB}\) is the sum of payments made by GPA and GPB. \(\left\{ {Q_{OS,GPA}^{TGC * * } ,Q_{OS,GPB}^{TGC * * } ,P_{i,t}^{G * * } } \right\}/\left\{ {C_{GPA,OS}^{TGC * * } ,C_{GPB,OS}^{TGC * * } } \right\}\) are their optimal decisions under the optimal of others.

Nash equilibrium in complete cooperation should meet the following relations:

$$\left\{ {Q_{OS,GPA}^{TGC * \prime \prime } ,Q_{OS,GPB}^{TGC * \prime \prime } ,P_{i,t}^{G * \prime \prime } ,C_{GPA,OS}^{TGC * \prime \prime } ,C_{GPB,OS}^{TGC * \prime \prime } } \right\} = I_{OS,GPA,GPB} \left( {Q_{OS,GPA}^{TGC} ,Q_{OS,GPB}^{TGC} ,P_{i,t}^{G} ,C_{GPA,OS}^{TGC} ,C_{GPB,OS}^{TGC} } \right)$$
(15)

where \(\left\{ {Q_{OS,GPA}^{TGC * \prime \prime } ,Q_{OS,GPB}^{TGC * \prime \prime } ,P_{i,t}^{G * \prime \prime } ,C_{GPA,OS}^{TGC * \prime \prime } ,C_{GPB,OS}^{TGC * \prime \prime } } \right\}\) is the optimal decision of complete cooperation.

The proof of the existence of Nash equilibrium in strategic game models can be found in the Appendix A.

Uncertainty analysis based on the distributed robust theory

Considering the uncertainty of wind power and photovoltaic output in green power plants, a distributed robust uncertainty analysis method based on the Bayesian model is proposed. This section uses Bayesian theory to construct a fuzzy set of uncertain probability distributions. Unlike traditional statistical inference, Bayesian updating preserves uncertainty and continuously updates the posterior probability based on newly obtained observations and prior probabilities. Among them, the multivariate nonlinear and mixed-effect based on Bayesian models are used to construct the fuzzy sets of the probability distribution of wind power and photovoltaic respectively. This method can make up for the defect of DRO that the construction of fuzzy sets is subjective and only for the description of uncertain parameter vectors under a single time section. In addition, Bayesian mixed effects models can simultaneously consider data information from various categories and the entire population, summarizing the learned information from all category data to improve prediction accuracy.

Bayesian model

The standard Bayesian theorem is as follows:

$$Pr\left( {\left. p \right|\varpi } \right) = \frac{{Pr\left( {\left. \varpi \right|p} \right)Pr\left( p \right)}}{Pr\left( \varpi \right)}$$
(16)

where, \({\varpi \mathord{\left/ {\vphantom {\varpi p}} \right. \kern-0pt} p}\) are parameters, represent the probability and times of an event observed in the sample data. \(Pr\left( {\left. \varpi \right|p} \right)\) represent the likelihood function, is a mathematical formula that defines the possibility of observation. \(Pr\left( p \right)\) represent the transcendental functions, is the initial distribution in the Bayesian model. \(Pr\left( \varpi \right)\) represent the Marginal likelihood function, is to standardize the posterior distribution.

Taking 24 h in a day as an example, the wind speed is less affected by time intervals, so the multivariate nonlinear model based on Bayesian is constructed for learning and fitting. The solar radiation intensity has obvious regularity and correlation with time intervals, so the Bayesian mixed effect model is used to deal with the uncertainty in different periods. The model can consider the information in each category and the whole group, and summarize the information to improve the accuracy of the prediction.

Wind power—the Bayesian multivariate nonlinear model

The wind power output is affected by the uncertainty of wind speed. The Pearson coefficient is used to measure the correlation between wind speed deviation and meteorological factors such as temperature, wind direction, and humidity. The results show that the wind speed deviation has highly positive with the wind speed, while has a lowly negative or weak with other factors. So, taking the standard value of the wind speed deviation as the result variable and the standard value of the predicted wind speed as the prediction variable, a multivariate nonlinear model is constructed:

$$\left\{ \begin{gathered} deviation_{i} \sim Normal\left( {\mu ,\sigma } \right) \\ \mu_{i} \sim a + b_{1} * Velocidad.s_{i} + b_{2} \left( {Velocidad.s_{i} } \right)^{2} \\ a\sim Normal\left( {\mu_{a} ,\sigma_{a} } \right) \\ b_{1} \sim Normal\left( {\mu_{{b_{1} }} ,\sigma_{{b_{1} }} } \right) \\ b_{2} \sim Normal\left( {\mu_{{b_{2} }} ,\sigma_{{b_{2} }} } \right) \\ \sigma \sim HalfCauchy\left( {\gamma_{\sigma } ,x_{0}^{\sigma } } \right) \\ \end{gathered} \right.$$
(17)

where \(Normal\left( {\mu ,\sigma } \right)\) represent the Gaussian distribution that the mean is \(\mu\), the variance is \(\sigma\). \(HalfCauchy\left( {\gamma_{\sigma } ,x_{0}^{\sigma } } \right)\) represent the Semi Cauchy distribution that the scale parameter is \(\gamma_{\sigma }\), the position parameter is \(x_{0}^{\sigma }\). \(deviation_{i}\) is the standard value of the wind speed deviation, \(Velocidad.s_{i}\) is the standard value of the predicted wind speed, the subscript i indicates the ith variable in the sample, \(deviation_{i} /Velocidad.s_{i}\) are both dimensionless after standardization. The first line in (17) is the likelihood function, assuming that it obeys the Gaussian distribution. \(\sigma /\mu_{a} /\sigma_{a} /\mu_{{b_{1} }} /\sigma_{{b_{1} }} /\mu_{{b_{2} }} /\sigma_{{b_{2} }} /\gamma_{\sigma } /x_{0}^{\sigma }\) are the parameters to be estimated, \(\mu_{a}\) are the mean and variance of \(a,\;\mu_{{b_{1} }} /\sigma_{{b_{1} }}\) are the \(b_{1}\)’s, \(\mu_{{b_{2} }} /\sigma_{{b_{2} }}\) are the \(b_{2}\)’s. \(\mu\) is the result of a nonlinear function composed of \(a/b_{1} /b_{2} /Velocidad.s_{i}\). The derivation process of the posterior distribution of the model and the posterior distribution results of all parameters are shown in Appendix B.

To visually display the results, Fig. 3 shows the regression line and prediction interval of the result variables. The horizontal/vertical coordinates are the standard value of the predicted wind speed and wind speed deviation.

The blue circle in Fig. 3 represents the original sample data, the solid line is the regression line for the mean of the result variable, and the surrounding two shadow areas represent two 89% confidence intervals. The narrower shadow indicates the distribution of the mean of the result variable, and the wider indicates the result variable’s.

Fig. 3
figure 3

The confidence interval of standard for predicted wind speed deviation at 89%.

Full size image

From the following relationship between wind speed and the output power of wind turbines43, the uncertain set of output power can be obtained.

$$P^{W} = \left\{ \begin{gathered} 0,V^{W} < V_{in}^{W} ,V^{W} > V_{off}^{W} \\ P_{R}^{W} \cdot \frac{{V^{W} - V_{in}^{W} }}{{V_{R}^{W} - V_{in}^{W} }},V_{in}^{W} \le V^{W} \le V_{R}^{W} \\ P_{R}^{W} ,V_{R}^{W} \le V^{W} \le V_{off}^{W} \\ \end{gathered} \right.$$
(18)

Photovoltaic—the Bayesian mixed effect model

The output power of PV is affected by the uncertainty of solar irradiation intensity. The Pearson coefficient is used to measure the correlation between irradiation intensity deviation and meteorological factors such as atmospheric temperature, pressure, and humidity. The results show that the radiation intensity deviation has a high positive with the radiation intensity, a medium positive with the atmospheric temperature, and a very weak with the others. Therefore, considering power output period is 9:00–18:00, taking the standard value of the irradiation intensity deviation as the result variable and the predicted irradiation intensity and temperature as the prediction variables, the Bayesian mixed effect model is constructed, as follows:

$$\left\{ \begin{gathered} Deviation.s_{i} \sim Binomial\left( {Time\left( i \right),p_{i} } \right) \\ \log it\left( {p_{i} } \right) = a + b_{i} * Radiacion_{i} + b_{2} * Temperature_{i} \\ a\sim Normal\left( {\mu_{a} ,\sigma_{a} } \right) \\ b_{1} \sim Normal\left( {\mu_{{b_{1} }} ,\sigma_{{b_{1} }} } \right) \\ b_{2} \sim Normal\left( {\mu_{{b_{2} }} ,\sigma_{{b_{2} }} } \right) \\ \sigma \sim HalfCauchy\left( {\gamma_{\sigma } ,x_{0}^{\sigma } } \right) \\ \end{gathered} \right.$$
(19)

Where, Binomial(n, p) is the Binomial distribution with the parameters n and p. Desviation.si is the standard value of the irradiation intensity deviation, Radiacion is the predicted irradiation intensity, Temperature is the predicted temperature, Time(i) represent the time category, the subscript i indicates the ith variable in the sample. Desviation.si is dimensionless after standardization. \(\sigma /\mu_{{b_{1} }} /\sigma_{{b_{1} }} /\mu_{{b_{2} }} /\sigma_{{b_{2} }} /\gamma_{\sigma } /x_{0}^{\sigma }\) are the parameters to be estimated. \(\mu_{{b_{1} }} /\sigma_{{b_{1} }}\) are the mean and variance of \(b_{1} ,\;\mu_{{b_{2} }} /\sigma_{{b_{2} }}\) are the \(b_{2}\)’s. \(\log it\left( {p_{i} } \right)\) represents the link function, and is defined as the log-likelihood ratio in Eq. (20). \(\log it\left( {p_{i} } \right)\) maps the parameter representing probability to another linear space on the whole real axis, and its definition domain is [0,1].

$$\log it\left( {p_{i} } \right) = \log \frac{{p_{i} }}{{1 - p_{i} }}$$
(20)

The derivation process of the posterior distribution of the model and the posterior distribution results of all parameters are shown in Appendix B.

To visually display the results, Fig. 4 shows the regression line and prediction interval of result variables in some periods. Each period has two subgraphs, the subgraph shows the relationship between the change of another prediction variable and the result variable when the value of the prediction variable (predicted irradiation or temperature) is the observation mean of the sample. The shaded shows an 89% confidence interval, the mean of the result variable (darker and narrower), and the result variable (lighter and wider). From Fig. 4, the means of the result variable under different categories (i.e. in different periods) are quite different, indicating that the mixed effect model can well describe the uncertainty of the result variable in each period.

Fig. 4
figure 4

Virtual graph of standard for radiation intensity deviation in each period.

Full size image

From the following relationship between irradiation intensity and the output power of PV43, the uncertain set of output power can be obtained.

$$P^{PV} = \left\{ \begin{gathered} P_{R}^{PV} \cdot \left( {\frac{{R^{PV} }}{{R_{\max }^{PV} \cdot R_{C}^{PV} }}} \right),0 < R^{PV} < R_{C}^{PV} \hfill \\ P_{R}^{PV} \cdot \left( {\frac{{R^{PV} }}{{R_{\max }^{PV} }}} \right),R^{PV} \ge R_{C}^{PV} \hfill \\ \end{gathered} \right.$$
(21)

Uncertainty analysis and robustness quantification

Taking wind power as an example, the hourly output of wind power is expressed as follows:

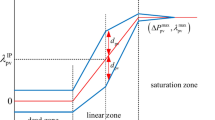
$$\left\{ \begin{gathered} P_{i,t}^{W} \in \left[ {P_{i,t}^{W - S} - \gamma_{i,t}^{W} \Delta P_{i,t}^{W - 1} ,\Delta P_{i,t}^{W - S} + \gamma_{i,t}^{W} \Delta P_{i,t}^{W - u} } \right],\forall i,t \hfill \\ \left\| {\gamma_{i,t}^{W} } \right\|_{\infty } \le 1,\left\| {\gamma_{i,t}^{W} } \right\|_{1} \le \Gamma_{t}^{W} \hfill \\ \left\| {\gamma_{i,t}^{W} } \right\|_{\infty } = \mathop {\max }\limits_{{1 \le i \le N^{W} }} \left| {\gamma_{i,t}^{W} } \right|,\left\| {\gamma_{i,t}^{W} } \right\|_{1} = \sum\limits_{i = 1}^{{N^{W} }} {\left| {\gamma_{i,t}^{W} } \right|} \hfill \\ \end{gathered} \right.$$
(22)

Where, \(\left\| {\gamma_{i,t}^{W} } \right\|_{\infty }\) is the infinite norm. \(\left\| {\gamma_{i,t}^{W} } \right\|_{1} \le \Gamma_{t}^{W}\) is the perturbation 1-norm, which corresponds to the spatial clustering effect of the actual wind power output. The spatial clustering effect can be explained as the fact that the power deviation of each wind farm during the same scheduling period cannot reach its maximum value at the same time44. It can provide a more detailed description of the volatility of uncertain variables, thus introducing the uncertainty spatial constraint parameter \(\Gamma_{t}^{W}\) of wind farms. \(\gamma_{i,t}^{W}\) is the deviation coefficient of ith wind plant at t.

According to Lindeberg levy central limit theorem \(\Gamma_{t}^{W}\) is expressed as follows (The derivation are shown in45):

$$\Gamma_{t}^{W} = N^{W} \cdot \mu + \Phi^{ - 1} \left( {\alpha^{W} } \right)\sqrt {N^{W} } \cdot \sigma ,\forall t$$
(23)

Where, \(\alpha^{W}\) is the confidence probability. Confidence probability is a concept in statistical inference that represents the likelihood of an event occurring under given conditions. It is commonly used to construct confidence intervals and express uncertainty in statistical estimation. The choice of confidence probability will affect the robustness of trading strategies; \(\mu\), \(\sigma\) are the mean and variance of \(\gamma_{i,t}^{W}\).

By constructing the Lagrange function and linear duality theory, \(\sum\limits_{i = 1}^{{N^{W} }} {P_{i,t}^{W} }\) in the extreme case can be expressed in Eq. (24), and the derivation is in45. In Eq. (24), in the most extreme case, only the deviation coefficient of the output of one wind farm is less than 1, set that wind farm is j.

$$\sum\limits_{i = 1}^{{N^{W} }} {P_{i,t}^{W} } = \sum\limits_{i = 1}^{{N^{W} - 1}} {\left( {P_{i,t}^{W - S} - \Delta P_{i,t}^{W - u} } \right)} + P_{i,t}^{W - S} - \left( {\Gamma_{t}^{W} - \left[ {\Gamma_{t}^{W} } \right]} \right)\Delta P_{i,t}^{W - u}$$
(24)

Similarly, the uncertain set of PV output can be constructed, and the expression of its spatial constraint parameters (\(\Gamma_{t}^{PV}\)) can be calculated, and the output power in extreme cases.

The robustness of the system is evaluated by the probability out of extreme cases (POE). If only the power deviation of wind is considered, POE can be expressed as follows, and the derivation is in44.

$$POE\; = \;p\left( A \right)\; = \;\exp \left( { - \frac{{\left( {\Gamma_{t}^{W} } \right)^{2} }}{{2N^{W} }}} \right)$$
(25)

\(p\left( A \right)\) is the probability of occurrence of event A. A represents the output power of wind is outside the uncertain set.

If other uncertain variables can be considered, recorded as event B, event C……. According to the full probability formula of independent event occurrence, the POE of multiple uncertain variables can be expressed as follows:

$$POE = P\left( A \right) + P\left( B \right) + \ldots + P\left( A \right) \cdot P\left( B \right)$$
(26)

The solution of the strategic game model

The Moth-flame optimization (MFO) is selected to solve the strategic game model. The algorithm uses the lateral positioning of the moth to ensure the local convergence ability. The strategic game models are dynamic optimization considering time change, and the decision variables are matrix variables. So to enhance the ability to solve large-scale optimization problems and improve the effectiveness and competitiveness, the following improvement strategies are introduced, the improve MFO (IMFO) is proposed.

  1. (1)

    To increase the diversity of the initial population, the average entropy strategy is introduced to initialize the population.

  2. (2)

    To improve the global search ability, the variable scale chaos strategy is used to disturb the optimal individual.

  3. (3)

    To increase the randomness of the population, Lévy flight is used to update the population again.

  4. (4)

    To balance the global and local searchability, the individual cooperation and competition in differential evolution algorithm DE are used to guide the optimal search.

The specific strategies are in43. The dynamic relaxation43 is used to handle the power balance and the quota constraints. Other constraints can be transformed into boundary conditions and processed directly by IMFO. The overall solution process is shown in Fig. 5.

Fig. 5
figure 5

The overall solution process of the strategic model.

Full size image

Case study

Basic parameter setting of the case

This section uses MATLAB R2015b to simulate on Windows 7PC (2.90 Ghz, 4GB RAM). GPA/GPB are wind power and PV stations group with the scale of 1500 MW/800 MW. Refer to Table 3 for the average value of on-grid and power generation cost of various power generation technologies in different areas in 2017 and the average selling price of electricity, make the following settings: the electricity selling price within OS is 609 $/MWh, the on-grid price of thermal power is 372 $/MWh, only consider onshore wind power and centralized PV and the on-grid price of them are both 450 $/MWh, the generation cost of renewable energy is 220 $/MWh. Reference46, set the maximum transaction price of GCP is 800 $/MWh, and the minimum is 200 $/MWh. The penalty for incomplete quota shall be greater than the maximum transaction price of GCP and set it to 900 $/MWh, and the recycling of green certificates shall be less than the minimum transaction price of GCP and set it to 150 $/MWh, the fund for recycling can come from the punishment of the obligation subject.

Table 3 The feed-in tariffs and generation cost of various types of power generation technologies in China in 2017.
Full size table

Set the \(\omega /\omega{\prime}\) in bilateral transactions to 1. Set \(\beta_{OS}\) to 1, since only one obligation subject is involved in, and set \(\beta_{GPA} /\beta_{GPB}\) to 1.5/1. In this paper, the actual data of Hami area in Xinjiang Uygur Autonomous Region is used. Through the comprehensive analysis of the annual data, and four typical days are extracted to represent the trading situation in the four seasons of spring, summer, autumn and winter, respectively. The load reference value and the prediction of solar radiation intensity and wind speed and temperature are shown in Fig. 6. The quota is 11%.

Fig. 6
figure 6

The reference and forecast values of 4 typical days.

Full size image

The operating and fuel cost coefficient of thermal units in OS is the same as those of the IEEE-39 bus system.

Equilibrium analysis under different strategic game

Solve the 5 strategic game models in Section "Photovoltaic—the Bayesian mixed effect model" to obtain the Nash equilibrium results. Without considering the influence of uncertainty on Nash equilibrium, the parameters of uncertainty variables under different models are uniformly set as: \(N^{W} /N^{PV}\) are both 20, and the confidence probability of GPA and GPB are both 99%. The payment of each participant and overall under different strategic game models are as follow:

Different strategic game models correspond to different degrees of competition among multi-participants in bilateral transactions. In the case of complete cooperation ({OS, GPA, GPB}), the total payment is the largest. Compared with the situation of non-cooperation ({OS}, {GPA}, {GPB}), the total payment increased by 1.85%/0.86%/1.80%/1.41% respectively in 4 typical days. The payment of OS increased by 5.87%/4.52%/8.25%/3.39%, while the GPA/GPB’s are decreased. The results show that the degree of competition will affect the strategic behavior and income of participants. complete cooperation can balance the interests of participants and obtain the strategy with the highest total income. From Table 4, when OS cooperates with GPA or GPB, its interest will be improved, especially with the GPA—higher priority parameters. However, when GPA or GPB cooperate with OS, their interests will be reduced, because cooperation reduces the price competition within the alliance. The results in the Table 4 provide important information for the supervision organization of the power market to predict this type of cooperation competition, regulate the punishment, and the recovery cost to provide a theoretical reference. On the premise of creating a transaction environment of the green certificates and promoting the cooperation of all participants to maximize the total profit, the authorities should also prevent malicious manipulation and improper cooperation and competition.

Table 4 The payment of each participant and overall under different strategic game models.
Full size table

The equilibrium comparison between non-cooperative and complete cooperation situations is shown in Fig. 7:

Fig. 7
figure 7

Equilibrium results under the different situations.

Full size image

From Fig.7, compared with (a, b), the output of the thermal unit is smaller in the situation of complete cooperation than that in the non-cooperation, and it is maintained at the lowest in several periods. Compared with (c, b), the transaction price fluctuates randomly in the non-cooperation, while in the complete cooperation the transaction price is lower, and the price fluctuation of GPA and GPB is more consistent and not obvious. Compared with (e, f), the risk of price fluctuation can be avoided in complete cooperation, the transaction electricity is also more in this situation. Therefore, the complete cooperation can not only avoid the risk of fluctuations in prices and electricity within the alliance and stabilize the supply and demand of green certificates, but also promote renewable energy to participate in GCP and reduce pollution emissions of thermal units.

The comparison of green certificate transaction electricity and price in different situations is shown in Fig. 8. It can be seen that when green power plants cooperate with OS, the transaction price will be reduced, which will cause the transaction electricity to be greater than that in the competitive situation and increase its proportion in the overall transaction electricity.

Fig. 8
figure 8

Comparison of transaction electricity and price under different situations.

Full size image

Stability analysis of complete cooperation

According to the results in Table 4, in the complete cooperation, if the total interests of the alliance are distributed based on the payment of participants, the alliance cannot be formed due to the unreasonable distribution. Driven by interests, GPA and GPB tend to form other alliances to obtain more interests. To ensure the stable existence of the alliance under the maximum overall income, according to the concept of stable distribution47, the conditions for stable distribution under the alliance structure \(C^{S} = \left\{ {OS,GPA,GPB} \right\}\) are obtained as follows (Eq. 27), and the kernel of the cooperative game for the characteristic function is further obtained, as shown in Fig. 9.

$$\left\{ \begin{gathered} x_{OS} + x_{GPA} + x_{GPB} = v\left( {\left\{ {OS,GPA,GPB} \right\}} \right) \hfill \\ x_{OS} + x_{GPA} \ge v\left( {\left\{ {OS,GPA} \right\}} \right) \hfill \\ x_{OS} + x_{GPB} \ge v\left( {\left\{ {OS,GPB} \right\}} \right) \hfill \\ x_{GPA} + x_{GPB} \ge v\left( {\left\{ {GPA,GPB} \right\}} \right) \hfill \\ \end{gathered} \right.$$
(27)
Fig. 9
figure 9

Stable distributions in the complete cooperation.

Full size image

It can be seen from Eq. (27) that there are countless possibilities for stable distribution in complete cooperation, and the dark area in Fig. 9 represents the stable distribution. Figure 9 illustrates the stable distributions of benefits among alliance participants under complete cooperation. The shaded regions represent stable conditions ensuring alliance stability, with variability observed across different days. A reasonable distribution of benefits is essential to maintain alliance stability; otherwise, participants may seek other alliances. The axes show each participant’s share, and the stable regions indicate possible benefit combinations that ensure stability. Overall, numerous stable distributions exist, influenced by participants’ contributions and income maximization.

Sensitivity analysis of Nash equilibrium

According to the analysis in Section "Uncertainty analysis and robustness quantification", the extreme power in GPA/GPB depends on their spatial constraint parameters (\(\Gamma^{W} /\Gamma^{PV}\)) respectively (in Eq. 24), while \(\Gamma^{W} /\Gamma^{PV}\) are determined by the confidence probability and the total number of uncertain variables (in Eq. 23). The overall interests for the situation of complete cooperation is the best, so the sensitivity of Nash equilibrium to the above factors is analyzed.

The influence of confidence probability

The total number of power station \(N^{W} /N^{PV}\) are both 20. The Nash equilibrium results in complete cooperation under different confidence probabilities (α) are explored. The spatial constraint parameters and the total payment under different α are shown in Table 5.

Table 5 The payment of the overall under confidence probability.
Full size table

From Table 5, with the decrease of α, the total payment in the typical day system increases as a whole. This is because as the α decreases, the uncertain set of power generation shrinks, and the lower boundary of the uncertainty set increases, which improves the power generation plan of GPA/GPB, and more green electricity can be traded. The above situation makes the green electricity increase, so the competition intensifies, the green certificate transaction price decreases and GPA/GPB obtain more profits through small profits and quick sales. The comparison of transaction prices when a = 99% and a = 30% are shown in Fig. 10.

Fig. 10
figure 10

The comparison of transaction price when a = 99% and a = 30%.

Full size image

Based on the above analysis, the confidence probability is the main factor affecting the economy of the system. The decision-maker can reduce the robustness of the system by adjusting the confidence probability of the uncertain set flexibly, to improve the economy.

The influence of spatial cluster effect

The total number of uncertain variables is subdivided into the following cases in Table 6, under which the total power of renewable energy power stations remains unchanged. The payment of each participant and overall in the second typical day in each case are shown in Table 6. The confidence probability of power generation is 98% in some cases.

Table 6 The parameters of uncertain variables under different Cases.
Full size table

From Eq. (23), increasing the total number of uncertain variables can increase the spatial constraint parameters under the same confidence probability. From Eq. (24), with the increase of spatial constraint parameters, the uncertain set shrinks, and the lower boundary increases. From Table 6, with the uncertain set shrinking, the generation uncertainty of GPA/GPB reduce. So in extreme cases, the power generation plan of GPA/GPB is improved, which reduces the price, makes small profits and quick turnover, and improves the participants and the overall payment. Furthermore, with the increase of spatial constraint parameters, the volatility of uncertain variables is described in more detail, which is reflected by the POE. Figure 11 shows the change of POE in each case when the confidence probability of power generation changes from 20 to 99%.

Fig. 11
figure 11

The relationship between spatial cluster effect and POE.

Full size image

The colors in the figure represent the magnitude of POE, ranging from blue to red. Blue indicates a low POE, meaning the predict outcomes are more accurate and have lower uncertainty. Green and yellow represent medium POE values, indicating moderate uncertainty in the predictions. Red signifies a high POE, meaning the predict outcomes have high uncertainty and a greater probability of exceedance. Thus, the color bar illustrates the relationship between prediction accuracy and uncertainty across different confidence levels.

In this Fig. 11, the changes in POE are not only influenced by the confidence probability but also heavily impacted by the spatial cluster effect. Different cases (case 1, case 4, case 6, case 8) represent varying degrees of the spatial cluster effect, which directly determines how the system behaves as the confidence probability changes. In case 1, as the confidence probability increases, the POE significantly decreases, and the blue region expands, indicating a lower POE. This suggests that, under a weak spatial cluster effect, the system’s stability is highly dependent on the confidence probability. As the confidence probability increases, the system uncertainty reduces, and its performance becomes more reliable, with a lower probability of exceeding expected values. In this scenario, the spatial cluster effect is weak, and the system’s volatility is mainly influenced by α, showing high prediction reliability with low POE. In these cases (e.g., Case 4 and Case 6), while the POE decreases as α increases, the reduction is less pronounced compared to case 1. The system uncertainty improves with higher confidence probability, but the spatial cluster effect still plays a significant role. Under moderate spatial cluster effects, confidence probability helps reduce POE to some extent, but overall system stability is limited, and there is still notable volatility. In case 8, the system exhibits a strong spatial cluster effect, where POE remains high throughout the entire range of confidence probability, even as α approaches 1. The absence of blue areas indicates that, under this scenario, the spatial cluster effect dominates system performance, and the confidence probability has little impact on reducing POE. This means that the system’s uncertainty is largely governed by the spatial cluster effect, and even with high confidence probability, the prediction remains unreliable with consistently high POE. Thus, the spatial cluster effect and confidence probability work together to influence the POE. In some scenarios, increasing the confidence probability can effectively lower POE, but in cases with strong spatial cluster effects, the confidence probability has limited impact, and the spatial cluster effect becomes the primary factor governing system stability.

Comparative analysis of uncertainty methods

In order to verify the effectiveness of the proposed uncertainty analysis method, three uncertainty analysis methods, including stochastic optimization, robust optimization, and Bayesian-based distributional robust optimization, are compared with each other under the fully cooperative mode with a typical day 2 as an example, and the payment of the overall and computation times are shown in Table 7.

Table 7 Comparison of different uncertainty analysis methods.
Full size table

Both stochastic and Bayesian-based distributional robust optimization provide relatively higher payments, with stochastic optimization offering a slight advantage. However, robust optimization delivers the lowest payments, which is likely due to its conservative nature. Robust optimization and Bayesian-based distributional robust optimization have significantly shorter computation times than stochastic optimization. Robust optimization, in particular, is the most efficient in terms of computation time. In conclusion, the Bayesian-based distributional robust optimization offers the best balance between payment and computation time, making it suitable for applications where both factors are critical. If higher payment is the priority and computation time is less of a concern, stochastic optimization might be preferred. However, for scenarios requiring computational efficiency and robustness, robust optimization is a more suitable choice.

Conclusion

A bilateral transaction model of GCP considering the technical characteristics of generation units is proposed to solve the problems such as the mismatch between supply and demand of green certificates and the reduction of transaction plans constrained by power grid operation. In the model, the DRO based on Bayesian theory is used to describe the uncertainty of generation power in green power plants. And the cooperative game theory is used to analyze the complex cooperation and competition relationship among multi-player. The conclusions are as follows:

  1. (1)

    Different strategic game models correspond to different degrees of competition among multi-participants in bilateral transactions. The complete cooperation mode can balance the interests of all participants and obtain the strategy with the highest total income. Policymakers could consider incentivizing cooperation by offering rewards for collective action to create a cooperative atmosphere in the green certificate market.

  2. (2)

    The analysis of multi-subject strategic cooperation mode provides important information for the electric power market regulatory organization to prejudge this type of cooperation-competition decision-making. It can prevent market manipulation, malicious tariff increases, and other undesirable behaviors brought about by improper cooperation and competition among participants. Based on the analysis, the supervisory organization can strengthen the supervision of the market and formulate a clear code of conduct to promote a stable and competitive trading environment.

  3. (3)

    To ensure the stability of the alliance, the complete cooperation model needs a stable distribution scheme, otherwise, the alliance cannot be formed. In order to design more robust trading mechanisms, regulators could develop guidelines or frameworks that promote transparent and fair distribution of benefits and ensure stable cooperation over time.

  4. (4)

    The complete cooperation model can not only avoid the risk of fluctuations in transaction prices and electricity but also promote the participation of renewable energy in GCP and reduce the pollution emission of thermal units. Policymakers should introduce mechanisms to reduce volatility in transaction prices, such as price floors or caps, while incentivizing green power manufacturers through subsidies or green certificate premiums to encourage the integration of renewable energy sources

  5. (5)

    The confidence probability of uncertainty has a significant impact on the payment of each participant and overall, and the spatial constraint parameters have a significant impact on the POE. According to the case study, the decision-maker can adjust the confidence probability and spatial constraint parameters to improve the interests of each participant and the alliance based on ensuring the conservatism of the transaction plan. At the policy level, this would help to find a balance between risk management and maximizing the benefits of green certificate trading.