Introduction

“The stream of our consciousness, […] like a bird’s life, seems to be made of an alternation of flights and perchings”, said the philosopher William James1. A fundamental observation that still puzzles many scientists. Like the seasons that transform our landscapes, the spontaneous fluctuations of the brain reveal very different brain configurations. Brain activity at rest is commonly characterized by the spontaneous fluctuations of regional brain fMRI signals. Dynamic functional connectivity (dFC), a recent expansion to traditional functional connectivity (FC) analysis, explores the short-term temporal changes in FC between distributed brain areas2 and goes beyond the typical assumption that functional networks are temporally static.

DFC matrices can be clustered into several “brain patterns”. These brain patterns are typically grouped using unsupervised k-means clustering, where the centroid of each cluster represents a pattern2,3,4. Temporal analysis of the dFCs shows that wakefulness and anesthesia-induced loss of consciousness exhibit a reorganizing repertoire of brain patterns. This repertoire corresponds to an ensemble of distinct and repeatable patterns of brain activity3,4,5. The conscious brain is the site of rapidly changing dynamics within a rich repertoire of brain patterns. Conversely, during anesthesia and disorders of consciousness, brain activity is expressed according to a more rigid and poorer repertoire of brain patterns (i.e., transitions between brain patterns are rare, and some brain patterns are seldom visited)3,4. In this case, the brain dynamic connectivity is reduced to the underlying anatomical connectivity3,4,6.

The representation and interpretation of brain patterns is still an area of ongoing research. Previous dynamic studies have examined the frequency of occurrences or stability of each brain pattern2,3 and have proposed to project fMRI data into two- or three-dimensional space7. However, they either do not take into account the spatiotemporal nature of the data or focus on task fMRI rather than rs-fMRI8,9. Thus, the study of low-dimensional space is a highly promising approach to model a fine-grained representation of brain patterns. This would require a full characterization of the optimal size of this low-dimensional space, taking into account the learning capacity of the model. Previous work in the literature supports the choice of a low-dimensional model to study brain dynamics. For example, dFCs have been shown to reflect the interplay of a small number of latent processes using clustering or PCA-based reduction techniques2,10, and latent linear models can also be used to estimate these underlying processes11. However, linear models may be inadequate if the mapping is nonlinear or, equivalently, if the learned manifold is curved. To address this issue, variational autoencoders (VAEs) have been implemented in several studies7,12,13. The probabilistic nature of such generative models holds great promise for exploring the data structure. Unlike discriminative models, VAEs are unsupervised models that do not require a labeled dataset. In the proposed work, the choice of architecture is supported by the pioneering work of Perl et al.7. They showed that when a VAE (which parameterized both the encoder and decoder using a multi-layer perceptron (MLP)) is trained with simulated whole-brain data from awake and asleep healthy volunteers, the learned representations showed faded states of wakefulness. The choice of the optimal latent space dimension remained an open question in their work. This choice is a trade-off between compressing only essential information and preserving data reconstruction.

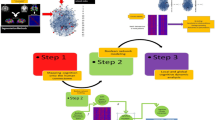
Here, we proposed a new interpretability framework, called VAE for Visualizing and Interpreting the ENcoded Trajectories (VAE-VIENT) between states of consciousness (Fig. 1). We took advantage of a previously acquired resting-state fMRI dataset in which non-human primates were scanned under different experimental conditions and across various states of consciousness: awake state and anesthesia-induced loss of consciousness using different anesthetics (propofol, sevoflurane, ketamine)3,4. After presenting the considered low-dimensional generative model, we showed that a 2D VAE has a balanced performance in reconstructing dFCs and classifying brain patterns. We then proposed a discrete and continuous characterization of the latent space. Finally, we showed that this model can translate some virtual modifications or inactivations of inter-areal brain connections into a transition of consciousness. The proposed virtual modifications or inactivations are not necessarily realistic but allow to illustrate the potential of the selected low-dimensional VAE.

Fig. 1
figure 1

Illustration of the proposed VAE-VIENT framework. A VAE learns 2D latent representations \(z=(z1_i,z2_i)\) from dynamic functional connectivity matrices (dFCs), leading to (1) evaluation of the proposed model against other generative models implementing different latent dimensions, (2) exploration of latent space with the ability to view discrete or continuous representations (here we observe how brain patterns are organized in latent space), and (3) two simulation paradigms, including a receptive field analysis that generates tensor representations to study the effect of perturbing input dFCs, and an ablation study of Global Neuronal Workspace (GNW) connections to study the transition from wakefulness to unconsciousness.

Full size image

Methods

Dataset

MRI acquisitions

This study used a rs-fMRI dataset previously acquired under different experimental conditions: awake state and anesthesia-induced loss of consciousness using different anesthetics (propofol, sevoflurane, ketamine)3,4. The data were collected for a previous project to discover a new signature of anesthesia-induced loss of consciousness. Here, we proposed a retrospective analysis of these data without additional experiments. In this way, we have maximized their use and shed new light on them.

Data were collected from five rhesus macaques (Macaca mulatta), one male (monkey J) and four females (monkeys A, K, Ki, and R), 5–8 kg, 8–12 years old, either in the awake state or under anesthesia (deep ketamine, moderate/deep propofol, or moderate/deep sevoflurane anesthesia), representing six conditions. Three monkeys were scanned for each experimental condition (awake: monkeys A, K, and J—propofol anesthesia: monkeys K, R, and J—ketamine anesthesia: monkeys K, R, and Ki—sevoflurane anesthesia: monkeys Ki, R, and J). Levels of anesthesia were defined by a clinical arousal score and continuous EEG monitoring (for details, see Uhrig et al.4). 156 rs-fMRI runs (31 for the awake state, 25 for moderate propofol, 30 for deep propofol, 25 for moderate sevoflurane, 20 for deep sevoflurane, and 25 for deep ketamine) of 500 volumes each were acquired on a 3T Siemens MRI with a customized single transmit-receiver surface coil, and a repetition time of 2.4 s.

In the original study, all procedures were conducted in accordance with the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes (Directive 2010/63/EU) and the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals. Animal studies were approved by the institutional Ethical Committee (Commissariat à l’Énergie atomique et aux Énergies alternatives; Fontenay aux Roses, France; protocols 10-003 and 12-086). The study is reported in accordance with ARRIVE guidelines14.

Pre-processing

The NeuroSpin Monkey (NSM) spatial preprocessing3,4 was applied, which includes the following steps: slice timing correction, B0 inhomogeneities correction, motion correction, reorientation, masking, realignment, and smoothing. Time series denoising operations were then applied3,4. Specifically, the voxel time series were detrended, filtered with low-pass (0.05-Hz cutoff), high-pass (0.0025-Hz cutoff), and zero-phase fast-Fourier notch (0.03 Hz, to remove an artifactual pure frequency present in all the data) filters, regressed against motion confounds, and z-score standardized. The denoised voxel time series were further averaged over the 82 cortical Regions Of Interest (ROIs) of the CoCoMac atlas15 and sliced into sliding time windows of 35 TR with sliding step of a 1 TR3. Classically, dFCs are estimated from the correlation between functional windowed time series. Such an estimate captures both direct and indirect statistical dependencies. Here, the regularized precision matrix is considered. It captures only direct statistical dependencies by discarding the effects of mediators. Specifically, an L1 penalty is applied using the Graph LASSO method. This penalty promotes sparsity but requires the choice of a regularization parameter \(\lambda\). As described by Barttfeld and colleagues3, this parameter is set to 0.1. The resulting connectivity matrix of size \(82 \times 82\) is Fisher transformed before further analysis. Repeating this procedure for each sliding window results in 72,384 dFCs.

Low-dimensional generative models

The Gaussian VAE

The emergence of deep learning-based generative models has spread to many disciplines, including medicine and neurosciences12,16,17,18. By learning and capturing the underlying probability distribution of the training data, generative models are able to generate novel samples with inherent variability. Three prominent families of generative models can be identified, namely generative adversarial networks, variational autoencoders (VAEs)19, and diffusion models. We focused on VAEs in this work. VAE training involves learning both an encoder to transform data as a distribution over the latent space and a decoder to reconstruct the original data (Fig. 1). The training minimizes the mean squared error reconstruction term, making the encoding/decoding scheme as effective as possible. Latent space regularity is enforced during the training to avoid overfitting and to ensure continuity (two nearby points in the latent space give similar content once decoded) and completeness (a code sample from the latent space should provide relevant content once decoded). These properties are at the core of the generative process. In practice, a regularization term constrains the encoding distributions to be close to a standard normal distribution using the Kulback-Leibler (KL) divergence.

Let’s consider a dataset \(D=\{X^{(1)},...,X^{(n)}\}\) with \(n=72,384\) dFC samples, where each sample \(X^{(i)}=[x^{(i)}_1,...,x^{(i)}_d]\) is a vector of \(d=3321\) dimensions (the dFC upper triangular elements). An autoencoder learns an identity function in an unsupervised way as follows:

$$\begin{aligned} \tilde{X^{(i)}} \approx f_\theta (g_\phi (X^{(i)})) \end{aligned}$$
(1)

where \(g_\phi (.)\) denotes the encoder, \(f_\theta (.)\) the decoder, and \(\tilde{X^{(i)}}\) is the network reconstruction of \(X^{(i)}\). The reconstruction loss, expressed as a Mean Squared Error (MSE), can be written as:

$$\begin{aligned} L_{MSE}(\theta , \phi ) = \frac{1}{n}\sum _{i=1}^{n}(X^{(i)} - \tilde{X^{(i)}}) = \frac{1}{n}\sum _{i=1}^{n}\left( X^{(i)} - f_\theta (g_\phi (X^{(i)}))\right) \end{aligned}$$
(2)

In this work, the VAE relationship between the input dFC data \(X^{(i)}\) and the latent encoding vector \(z^{(i)}\) was defined with a prior \(p_\theta (z^{(i)}) \sim \mathcal {N}(z^{(i)}; 0, 1)\), the likelihood \(p_\theta (X^{(i)}|z^{(i)})\), and the posterior \(p_\theta (z^{(i)}|X^{(i)})\). Unlike (finite) Gaussian mixture models, the posterior \(p_\theta (z^{(i)}|X^{(i)})\) is intractable. Therefore, we used a posterior approximation \(q_\phi (z^{(i)}|X^{(i)})\) which produces what is a likely code given an input \(X^{(i)}\). In our case of Gaussian VAE, \(q_\phi (z^{(i)}|X^{(i)}) = \mathcal {N}(z^{(i)}; m_\phi (X^{(i)}), s_\phi (X^{(i)}))\), where \(m_\phi\) and \(s_\phi\) are expressive parameterizations of the conditional mean and variance of \(q_\phi (z^{(i)}|X^{(i)})\). The distributions returned by the encoder are further constrained to follow a standard normal distribution as follows:

$$\begin{aligned} L_{KL}(\theta , \phi ) = D_{KL}(q_\phi (z^{(i)}|X^{(i)})||p_\theta (z^{(i)})) \end{aligned}$$
(3)

where \(D_{KL}\) is the KL divergence. A regularization parameter \(\beta\) was further introduced to learn disentangled representations and increase interpretability20,21. The idea is to keep the distance between the real and the estimated posterior distribution small while maximizing the probability of generating real data. A high \(\beta\) value emphasizes statistical independence over reconstruction. The final VAE loss was expressed as follows:

$$\begin{aligned} L_{VAE}(\theta , \phi ) = L_{MSE}(\theta , \phi ) - \beta L_{KL}(\theta , \phi ) \end{aligned}$$
(4)

The considered generative models

We considered a VAE with a one (\(\hbox {VAE}_1\)), two (\(\hbox {VAE}_2\)), or three (\(\hbox {VAE}_3\)) dimensional latent space, adapting the architecture proposed in Perl et al.7. The input was the upper triangular dFCs (as each dFC is symmetric). Then, the encoder part used two hidden fully connected layers (512 and 256 units, respectively) with ReLU activation functions, and the decoder part was implemented with the same structure. The dimension of the latent space corresponds to common neurobiological assumptions made when studying disorders of consciousness22,23,24. Furthermore, we compared our models with the sparse VAE (sVAE)25, initialized with thirty-two latent dimensions. The sVAE implemented a variational dropout to enforce parsimony and interpretability in the latent representations. A threshold on the dropout rates was used to select the optimal number of latent dimensions. We also applied a baseline machine learning model, the probabilistic PCA (PPCA)26, and compared the results to those obtained with VAE/sVAE. Indeed, PPCA can be considered as a latent variable model. Its assumptions are Gaussian distributions and linear decomposition. The purpose of adding this model was to assess the interest in nonlinear models such as VAE or sVAE when working with small datasets.

Model training

We trained the VAE and sVAE using an Adam optimizer, with a learning rate starting at 0.001 and a \(10\%\) decay every 30 epochs. To limit overfitting during the training, we included early stopping. The model was trained on the training set until its error on the validation set increased, at which point the optimization stopped. As a performance measure to monitor the stopping of training, we considered the sliding median using a 10 epoch interval. In addition, the patience argument allowed training to continue for up to 15 epochs after convergence. This gave the training process a chance to get over flat areas or find additional improvements. We used a batch size of 128. Using cross-validation, we studied the effect of the \(\beta\) regularization parameter for the VAE by performing a grid search to determine the better choice for \(\beta \in [0.5, 20]\) with the following user-defined steps [0.5, 1, 4, 7, 10, 20]. With the intention of building an interpretable model, we kept eight models: \(\hbox {PPCA}_1\), \(\hbox {PPCA}_2\), \(\hbox {PPCA}_3\), \(\hbox {VAE}_1\), \(\hbox {VAE}_2\), \(\hbox {VAE}_3\) with 1, 2, and 3 latent dimensions respectively, sVAE, and PPCA with the same number of latent variables selected by the sVAE. We performed a leave-one-subject-out to create an independent test set and a training set with an internal 5-fold cross-validation. In the cross-validation, the stratification of the experimental conditions further strengthens the distribution of the classes in each training split. In the end, only the weights associated with the best validation fold were evaluated on the independent test set.

The labels and pseudo-labels used were the experimental conditions (awake and the different anesthetics), and the brain patterns (BPs) ranked in ascending order of similarity to the structural connectivity (numbered 1–7), respectively. Briefly, the use of seven brain patterns has been shown to be effective in representing the different configurations of the brain3,4. Choosing the optimal number of brain patterns is challenging. It results from balancing biological assumptions and computational evaluations. These labels are known to be unevenly distributed across experimental conditions. They are also known to be good descriptors of spontaneous fluctuations in brain activity.

Model evaluation

Choosing an appropriate model is a trade-off between compressing only essential information and preserving data reconstruction. Thus, we evaluated the models using two distinct metrics. The first metric was a measure of the reconstruction quality. The second one was a measure of the regularity of the latent space organization, calculated using a classification task. Both used as labels the seven brain patterns previously described3,4.

Reconstruction quality

From the retained trained generative models, we computed the decoded dFC matrices \(\tilde{X^{(i)}}\) associated with the test set. Instead of using the MSE training loss, we evaluated the Pearson product-moment correlation coefficients between the averaged decoded dFCs and empirical averaged dFCs associated with each label. The Pearson correlation was calculated by taking the upper triangular elements of the z-transformed averaged FCs because the FC values are symmetric with respect to the diagonal. In addition to this metric, we measured reconstruction quality with two other metrics, SSIM27,28 and geodesic distance29. This metric ranges from \(-1\) to 1, inclusive, where 1 is a perfect match. Note that this metric is used only during the evaluation of the model.

Classification accuracy

From the retained trained models, we also computed the latent representations associated with the test set. In addition to the BP labels available from the dataset, we also matched each test dFC latent space location to its nearest location in the train set and retained the corresponding matched label. Balanced accuracy (BAcc) was then used to compare the dataset and matched BP labels. The BAcc is defined as the average of recall obtained on each class, as in the Scikit Learn Python library30,31,32.

Consensus metric

We proposed a consensus metric \(\mathcal {M}\), which is an average between reconstruction quality metric and BAcc. The goal was to enforce a trade-off that imposed spatial coherence in the latent space without significantly degrading the reconstruction quality.

Latent space exploration

Discrete and continuous descriptors

All the information we can transfer in latent space is associated with encoder-generated representations and is discrete by nature. Semantically continuous representations are required to build a comprehensive whole-brain computational model. With the generative capabilities of the VAE (or generative models in general), it is possible to decode the entire latent space. Without losing generality, let us give the formula in 2D. Let’s consider a discrete grid \(G \in R^2\) with \(g \times g\) latent samples and the associated decoded dFCs \(\tilde{X_{lm}}\), with \(l \in [1, g]\) and \(m \in [1, g]\). Using the previously known information on the brain patterns, we could label each \(\tilde{X_{lm}}\). To this end, and as suggested by Perl et al.7, we computed the similarity between each \(\tilde{X_{lm}}\) and each brain pattern. To assess the strength of these associations, we used Pearson’s correlation. At the end, the label assigned to \(\tilde{X_{lm}}\) is the number of the most correlated brain pattern. The obtained continuous labeling reflects the functional reconfiguration of the brain.

Confidence level of continuous descriptors

In addition, by quantifying the best association strength, we proposed to compute confidence and reliability maps associated with the continuous descriptor generation process. First, the confidence map \(\mathcal{C}\mathcal{M}\) was derived at each latent space location (l, m) by taking the average of the difference between the two largest associations and the correlation between the two closest brain patterns. Let \(\bar{BP^{lm}} = {\bar{BP^{lm}_1},..., \bar{BP^{lm}_7}}\) be the set of brain patterns ranked in ascending order of similarity to the decoded dFCs \(\tilde{X^{lm}}\) and \(\mathcal {R}\) is the Pearson correlation. The confidence map \(\mathcal{C}\mathcal{M}\) is given by:

$$\begin{aligned} \mathcal{C}\mathcal{M}^{lm} = \frac{1}{2} \left( (\mathcal {R}(\tilde{X^{lm}}, \bar{BP^{lm}_1}) - \mathcal {R}(\tilde{X^{lm}}, \bar{BP^{lm}_2})) + \mathcal {R}(\bar{BP^{lm}_1}, \bar{BP^{lm}_2}) \right) \end{aligned}$$

This metric considers both the reluctance to label and the objective nature of that reluctance. The model is reasonably confident when \(\mathcal{C}\mathcal{M}_{lm} \approx 0.5\), and overconfident when \(\mathcal{C}\mathcal{M}_{lm} \approx 1.0\). Second, the reliability map \(\mathcal{R}\mathcal{M}\) was expressed at each latent space location by decoding the dFC and targeting the brain pattern with the highest Pearson correlation:

$$\begin{aligned} \mathcal{R}\mathcal{M}^{lm} = \mathcal {R}(\tilde{X^{lm}}, \bar{BP^{lm}_1}) \end{aligned}$$
(5)

The higher \(\mathcal{R}\mathcal{M}_{lm}\), the more reliable the model is.

Connection-wise simulations

The receptive field analysis

If we consider brain dynamics as a physical process characterized by gradual changes in the FC space, then the dFCs used are samples of these changes. Physicists tried to model these processes in a principled way by analytically identifying prior knowledge about the underlying processes, e.g., by using differential equations33. Instead of incorporating physical knowledge into a deep neural network, we proposed a receptive field (RF) simulation paradigm to generate a tensor model of latent space and thus gain insight into its dynamics. Such a characterization of latent space is essential for building an interpretable model, and it can help understand encoded latent trajectories between states of consciousness. We proposed to capture the latent space RF at the connection level. In this way, the proposed RF analysis could identify the connections that need to be disrupted to move from one state of consciousness to another.

In more detail, the RF analysis focused on the trained VAE (or another generative model) encoder. A perturbation was simulated at each connection \(j \in [1, d]\) of an input dFC matrix \(X^{(i)}\) (Fig. 2-A). The effect of this perturbation on the encoded latent representations was tracked (Fig. 2-B)16. In particular, the simulation modified a single connection value \(x_j^{(i)}\)p times, by swapping its value with a correlation drawn uniformly in an interval \([-1, 1]\), while keeping the other connections fixed. In two dimensions, the latter simulation yielded p latent encoded vectors \(z_j^{(i)} = \{z_{j1}^{(i)}\),..., \(z_{jp}^{(i)}\} \in \mathbb {R}^{p \times d}\). The generated latent samples \(z_j^{(i)}\) were distributed around a line of varying length. This specific behavior allowed an interesting parameterization of each perturbation, using polar (in 2 dimensions) or spherical (in 3 dimensions) coordinates, through the inclinations \(\theta _j^{(i)}\) (Fig. 2-B). The perturbation of all connections returned a cloud of points describing the RF. The resulting cloud had an ellipsoidal shape \(\mathcal {E}\), estimated with a confidence interval of 0.01. \(\mathcal {E}\) can be parameterized by its sorted eigenvalues \(\lambda _i\) and associated eigenvectors \(\vec {e_i}\), \(i \in [1, N]\), where N is the latent dimension. Finally, since each connection can be related to a direction by the inclination angle \(\theta _j^{(i)}\), it was possible to select the connections with high potential for action (i.e., generating the highest brain transitions when perturbed) by identifying the directions aligned with the first eigenvector \(\vec {e_1}\) of the ellipsoid \(\mathcal {E}\). The procedure described above can be applied to any dFC. Any dFC can be projected onto a point in latent space around which an ellipsoid representing the effect of all possible unit perturbations was computed.

Fig. 2
figure 2

Illustration of the two steps involved in the receptive field analysis. (A) From a dFC matrix \(X^{(i)}\), or equivalently its upper terms \(x^{(i)}\), two perturbations are performed on connections b (blue) and r (red) by swapping one connection with the following three correlations \([-1, 0, 1]\) (\(p=3\)). (B) Corresponding \(z_b^{(i)}\) and \(z_r^{(i)}\) latent representations (\(N=2\)) follow lines and are summarized by their inclination angles with the x-axis \(\theta _b\) and \(\theta _r\), respectively.

Full size image

The ablation analysis

In machine learning, feature ablation study allows to find the importance of features in a model. In our case, we observed how removing a subnetwork affects the model’s latent representations and performances. Such a technique helped us to identify which subnetworks contribute to the anesthesia-induced loss of consciousness. Stemming from our previous work in which we identified fundamental networks underlying consciousness in the macaque brain34,35, we virtually inactivated specific brain areas. We tested the ability of the trained VAE to predict transitions across consciousness levels efficiently. For this, we simulated specific inactivations/ablations of functional connections between brain areas as a virtual experiment. The resulting dFC representations were then used to predict the state of consciousness. Using the framework of the Global Neuronal Workspace (GNW) theory of consciousness, we previously identified major brain areas (referred to as “macaque GNW nodes”) that account for the cortical signature of consciousness realizing a fronto-parieto-cingular network34,35. The key brain regions whose associated connections were zeroed in this study were the posterior cingulate cortex (CCp), the anterior cingulate cortex (CCa), the intraparietal cortex (PCip), the frontal eye field (FEF), the dorsolateral prefrontal cortex (PFCdl), the prefrontal polar cortex (PFCpol) and the dorsolateral premotor cortex (PMCdl) of the left and right hemispheres4,35. Thus, we proposed a connection-wise ablation study, equivalent to a lesion perturbation, that removed the contribution of connections linked to these regions. It’s important to note that removing a region removes all connections associated with that region. By zeroing these connections, we expected to shift dFCs acquired in the awake state to an anesthetized state.

We trained an SVM classifier on the learned latent representations to predict the awake and anesthetized states. We then evaluated the performance of the classifier in predicting the awake state using the balance accuracy (BAcc). To focus on the effect of the proposed ablation and to eliminate any unrelated source of variability, the analysis was performed on the training set only. As input to the trained SVM, we took only the raw or perturbed awake dFCs (i.e., awake dFCs undergoing the ablation process) encoded with the VAE. We denoted the corresponding prediction scores as BAcc and \(\tilde{BAcc}\), respectively. To assess the specificity of zeroing these nodes, we tested the null hypothesis that removing random connections did not result in a significant loss of prediction compared to targeted GNW-associated connections. Let \(G=14\) be the number of GNW nodes. Our goal was to modify G nodes that were not part of the GNW. The cardinality of the corresponding universe \(\Omega\) of all possible combinations is large. Therefore, we drew a subset of \(M=1000\) samples from \(\Omega\) without replacement. Finally, we evaluated the associated awake prediction performances \(\bar{BAcc}^i\), \(i \in [1, M]\). Using this null distribution statistic, we computed a one-tailed empirical p-value for \(\tilde{BAcc}\) by looking at the proportion of values less than or equal to the observed value when all GNW-related connections were removed36.

VAE maps the distribution of dFC to another distribution in a latent space. Technically, this mapping is only valid around the distribution of dFC you used for training. If the perturbed dFC pattern is out of distribution, then the mapping can be arbitrary. And further analyzing this mapped dots in this latent space may not be meaningful. For example, if the input is out of the training data distribution, the reconstructed loss with the decoder could be much larger compared to the ones that are in distribution. To test if the input is out-of-distribution, we quantified the reconstruction loss after ablation compared with the reconstruction loss on the original data by calculating the difference between the two Pearson correlations.

Results

Model evaluation

In our experiments, the final number of epochs varied in the interval [159, 1359] when the early stopping criterion was applied. The variational dropout in the sVAE selected 15 of the 32 latent dimensions (see Appendix S1). To evaluate whether a low-dimensional VAE can achieve reasonable assumptions, we compared several generative models with different parameters (\(\hbox {PPCA}_1\), \(\hbox {PPCA}_2\), \(\hbox {PPCA}_3\), \(\hbox {PPCA}_{15}\), \(\hbox {VAE}_1\), \(\hbox {VAE}_2\), \(\hbox {VAE}_3\), and \(\hbox {sVAE}_{15/32}\)). This allowed a quantification of how the latent representations stratify the brain patterns and how a model can reconstruct the input dFCs from the low-dimensional representations.

Balancing reconstruction quality and regularization

By looking at the Pearson correlation coefficient for all models (Fig. 3-A), we observed that (1) the chosen \(\beta\) had little effect on the VAE reconstructions, but (2) decreasing the latent space dimension degraded the reconstruction, and (3) nonlinear low-dimensional models had higher reconstruction quality. Higher dimensional models are expected to perform better because they capture more variability, resulting in a better reconstruction. We further quantified the decrease in reconstruction quality by comparing the \(\hbox {VAE}_2\) with the \(\hbox {sVAE}_{15/32}\). The cost of a low-dimensional, more interpretable model was approximately a 0.06-point decrease in Pearson correlation coefficient. It also appeared that a nonlinear model can reconstruct better with fewer latent dimensions. Monitoring the Pearson correlation coefficient brain pattern-wise also showed that not all brain patterns were reconstructed similarly with a Pearson correlation coefficient in the [0.55, 0.95] range (Fig. 3-D). Interestingly, the reconstruction quality increased with the number associated with each brain pattern. Thus, the models reconstructed the brain patterns closer to the structural connectivity (with a simpler topology) more accurately. The trend observed is the same with the two other metrics (SSIM and geodesic distance) (see Fig. 4 & Appendix S7). Since geodesic distance is a dissimilarity metric, the higher it is, the more dissimilar the matrices.

Fig. 3
figure 3

Brain pattern (BP) classification/reconstruction using VAE, PPCA, and sVAE models: (A) the Pearson correlation coefficient of BP-wise averaged dFCs with respect to the model parameters, (B) the balanced accuracy (BAcc) between the ground truth and the matched predicted label, (C) the proposed consensus metric \(\mathcal {M}\), and (D) the Pearson correlation coefficient recorded for each BP. In plots A, B, and C, the selected \(\hbox {VAE}_2\) is highlighted by a red bounding box. The dashed lines represent the trends obtained for each latent space dimension across the considered models.

Full size image

Balancing classification accuracy and regularization

Monitoring the classification accuracy (Fig. 3-B), we observed that the BAcc (1) increased as \(\beta\) increased, (2) decreased as the latent space dimension decreased, except in high dimensions (i.e., for the \(\hbox {sVAE}_{15/32}\)), and that (3) the linear PPCA baseline outperformed other models in high dimensions (\(\hbox {PPCA}_{15}\)). Overall, the classification scores were relatively high for a seven-class classification problem. For all considered models, the BAcc scores ranged from 0.45 to 0.75 (to be compared to the theoretical chance level of 0.14). The classification accuracy metric favored the use of the highest regularization parameter (\(\beta =20\)), which promotes coherence in the latent space. Furthermore, better performance (an increase of 0.06-point) and lower interfold variance were observed for the 3D VAE (\(\hbox {VAE}_3\)) models. Notably, the \(\hbox {sVAE}_{15/32}\) performed poorly, suggesting that a few latent dimensions were preferable to encode the brain pattern information.

Balancing reconstruction and classification

As the number of latent dimensions increased, the model captured more variability, including noise. Furthermore, limiting the number of latent dimensions improved the brain pattern detection task. This trend confirmed that dFCs reflected the interplay of a small number of latent processes2,10. Looking at the consensus metric (Fig. 3-C), we specified the following model for the rest of the paper: a 2D VAE (\(\hbox {VAE}_2\)) with a \(\beta =20\) regularization parameter. Using these parameters, we enforced a trade-off that imposed spatial coherence in the latent space without significantly degrading the reconstruction quality. Finally, we showed that the reconstructed brain patterns (as the reconstructed dFCs averaged over the different brain patterns) recovered the dominant structures obtained with a k-means clustering of the dFCs (Fig. 4). The same model evaluation can be performed using experimental conditions as labels (see Appendix S2). To clarify the notation, the selected \(\beta _{20}-VAE_2\) will be referred to as VAE in the following.

Fig. 4
figure 4

The brain patterns (BPs) from the k-means clustering and after reconstruction with the selected \(\beta _{20}-VAE_2\) The distance between the original and reconstructed centroids is displayed, for various metrics. SSIM distance = 1 − SSIM; Correlation distance = 1 − Pearson correlation.

Full size image

Latent space exploration

To investigate the potential of latent representations to decode states of consciousness, we considered two types of descriptors: discrete and continuous latent representations. The latter are exploited thanks to the generative properties of VAEs. Again, we focused on the stratification of latent representations according to brain patterns. We also considered the reliability of the generated continuous descriptors.

Stratification of brain patterns

From the VAE encoder, we obtained discrete latent representations. The ground truth labels were the brain patterns ranked in ascending order of similarity to the structural connectivity (numbered from 1 to 7). We examined the discrete composition of the latent space using the brain pattern labels (Fig. 5-A) and the calculated lifetime (Fig. 5-B). The lifetime is defined as the time spent continuously in a brain pattern (i.e., when no transition is observed). Therefore, all dFCs on this time axis have the same lifetime. Our focus was on three main properties of latent space. First, the resulting discrete representations formed a cloud of points rather than a set of clearly separable clusters. Second, the generated latent representations were remarkably well stratified when looking at the brain pattern labels (Fig. 5-A). Each brain pattern was isolated while no constraint was enforced during training. To quantify the overlap between brain patterns, we chose the Dice similarity coefficient. The Dice metric yields values between 0 (no spatial overlap) and 1 (complete overlap)37. Overall, the average Dice metric remained relatively low (\(<0.37_{\pm 0.19}\)), confirming that the spatial overlap between brain patterns was small (see Appendix S3 for details). Interestingly, brain pattern 7 (the one closest to the brain structure) occupied a central position in the representation space and had the highest Dice coefficient. Third, the central locations, aligned with brain pattern 7, had longer lifetimes (Fig. 5-B). Note that we verified the absence of subject bias prior to analysis and also illustrated the stratification of the learned latent space with respect to the experimental conditions (see Appendix S4). We also verified that the proposed VAE reliably encoded the dFC time courses while no constraint was enforced during training (see Appendix S5).

Fig. 5
figure 5

Discrete stratification of the latent space of the selected VAE into a base of (A) Brain Patterns (BPs)—the centroids from a seven-class k-means clustering on the dFCs and (B) lifetimes - the time spent continuously in the corresponding brain pattern. Note that the obtained BP stratification mainly shows non-overlapping clusters as quantified in Appendix S3. For the lifetimes, we discretize the values into three categories: the 25% longest (in red), the 25% shortest (in blue), and all others medium (in pink).

Full size image

Toward a whole-brain computational model

By exploiting the generative capabilities of VAE, we obtained semantically continuous representations in the latent space, which promoted versatility. The generated continuous brain pattern labels covered the entire latent space. They also showed a pooled organization of the brain patterns (i.e., each brain pattern was mostly composed of a single connected component) (Fig. 6-A). The accuracy of the brain pattern matching process was measured by the confidence \(\mathcal{C}\mathcal{M}\) and the reliability \(\mathcal{R}\mathcal{M}\) maps. Interestingly, the most noteworthy trend was that brain pattern boundaries were less reliable than central locations (Fig. 6-C and D). With these maps, we gained confidence in using continuous descriptors in the latent space. Finally, decoding dFCs on a \(19 \times 19\) regularly sampled grid in the latent space highlighted the learned manifold structure. Noteworthy, it exhibited brain patterns gradient toward the origin (Fig. 6-B). Overall, the generated low-dimensional representations captured dynamic signatures of fluctuating wakefulness.

Fig. 6
figure 6

Continuous stratification of the latent space of the selected VAE and corresponding confidence and reliability maps: (A) continuous representation of the Brain Patterns (BPs), (B) decoded dFCs sampled using a regular \(19 \times 19\) grid in the latent space, (C) estimated confidence map \(\mathcal{C}\mathcal{M}\), and (D) estimated reliability map \(\mathcal{R}\mathcal{M}\). A, C, and D used a regular \(200 \times 200\) grid in the latent space.

Full size image

Connection-wise simulations

We used external perturbations to characterize the representation of different states of consciousness better. To this end, we first studied the shift in latent space induced by modifying a single connection of a dFC matrix. Using receptive field analysis, we could identify preferred directions for moving from one state to another. Second, we proposed an ablation analysis to ensure that dimension reduction preserves critical information about consciousness. For the latter, specific connections related to the regions highlighted by one of the major theories of consciousness (the GNW) were zeroed, and we examined the induced displacement in latent space.

Perturbation of connections to study transitions

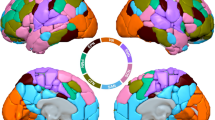
Using connection-wise RF analysis, a tensor \(\mathcal {E}\) was estimated at each latent space location. We proposed to focus on seven specific latent space locations that were obtained when encoding the seven brain patterns with the VAE (see the central plot in Fig. 7). From each obtained tensor, we characterized the overall potential for action (i.e., the chance of generating a brain pattern transition) by the mean diffusivity (MD) (obtained by averaging the tensor eigenvalues). We found that this potential for action was always present but was small, lying in the interval [0.0068, 0.023]. Nevertheless, all tensors obtained were anisotropic. Thus, it was possible to select the connections with the highest probability of generating a brain pattern transition. In this study, we kept twenty connections (see circular plots in Fig. 7). Interestingly, the MD for \(BP_7\) was minimal, making it a “stable” pattern (i.e., a perturbation of this pattern is unlikely to cause a shift in consciousness).

Fig. 7
figure 7

Results of RF analysis of the seven brain patterns and associated connections with a high potential for action. Using the proposed connection-wise RF analysis, a local perturbation model computed as an ellipse is derived at each encoded latent space location. Note that to improve readability, we scaled each ellipse. The associated mean diffusivity (MD) is calculated. For each ellipse, the twenty connections that cause the most displacement in the latent space are displayed using a circular layout. The connectivity plots were generated with MNE-Python: 1.6.038.

Full size image

Ablation of connections for virtual experiments

First of all, to test if the input is out-of-distribution after the ablation, we quantified the reconstruction loss after ablation compared with the reconstruction loss on the original data. We did observe a loss of reconstruction, but this remains reasonable (around 0.2 correlation points) and the reconstruction similarity values remain high (around 0.8) (cf. Appendix S8). So we can watch what is happening in latent space without the risk of arbitrary mapping. This connection-wise ablation study showed an apparent decrease in BAcc in wakefulness prediction when the GNW-associated connections were removed (\(\tilde{BAcc}<< BAcc\) in Fig. 8). As mentioned above, the zeroed connections involved brain regions that were considered part of a critical cortical network for consciousness. We verified the significance of this decrease compared to random connection-wise ablations (\(p_{val}=0.008\)). Thus, we showed that a realistic state transition can be obtained by modulating a network involved in consciousness. The connection-wise ablation study highlighted the relevance of the information captured in latent representations and supported the ability of the trained VAE to be an attractive computational model to decode and predict states of consciousness. To further support this claim, we consider two different combinations of GNW areas in the proposed ablation study. In the first experiment, we group anterior areas (FEF, PMCdl, CCa, PFCpol) and posterior areas (PCip, CCp, V1). The proposed experiment is part of the heated debate about the role of the front and the back of the brain in the neural correlates of consciousness39. The obtained SVM scores are 0.57 and 0.62, respectively, indicating that both constructed subnetworks play almost the same role in conscious access and that partial ablation is insufficient for a change of consciousness state. Broad ablation is needed to force a transition between states of consciousness. In the second experiment, the GNW key areas are extended to include the primary sensory regions, primary somatosensory cortex S1, primary auditory cortex A1, and visual area V1. The addition of these areas further increases the transition to an anesthetized state and the statistical significance of the results (see Appendix S6—Fig. 1). This result is consistent with the literature where these areas have been shown to play an essential role in conscious access40.

Fig. 8
figure 8

Ablation study performed from the GNW nodes. We evaluate the performance of a trained SVM classifier in predicting the awake state using balance accuracy (BAcc). As input, we take only the raw or perturbed awake dFCs. We denote the corresponding prediction scores as BAcc (vertical red dot line) and \(\tilde{BAcc}\) (vertical blue dot line), respectively. We also display the histogram of \(\bar{BAcc}^i\) when random connections are removed.

Full size image

Discussion

We proposed the VAE-VIENT framework as a tool to decode consciousness-related brain patterns from brain activity, to visualize their organization, and the transitions within the patterns that underlie states of consciousness in macaques. A VAE generative model has already been used to capture the different states of consciousness in a low-dimensional latent space. Here, we showed that such a model with tailored low-dimensional representations can be used to characterize brain dynamics over the dFCs. With low 2D-dimensional representations, the obtained performances were better than with other linear (here, the PPCA) and nonlinear (here, the sVAE) generative models. However, this trend was not confirmed in higher dimensions (especially in 15D). It is generally accepted that simple models of neural mechanisms can be remarkably effective. We showed that a 2D VAE model could (1) generate a latent feature space stratified into a base of brain patterns and (2) reconstruct new brain patterns coherently and stably despite the limited dataset size by exploiting the generative part of the model. We argued that the VAE-VIENT framework provided a simulation-based whole-brain computational model. Indeed, we showed that the tensor fields generated from the RF analysis could model brain pattern transitions and that the proposed ablation analysis provided a unique way to select target connections/regions non-invasively. These findings paved the way for medical applications such as depth of anesthesia monitoring, coma characterization, and accurate diagnosis of disorders of consciousness in patients.

Dataset and preprocessing limitations

The settings of this study have four major limitations. First, our dataset is relatively small, which increases the risk of overfitting. Tests on larger cohorts will be needed to validate our observations, as with studies of sleep and consciousness disorders in humans2,6,41 even if these datasets are also limited. However, they can be useful for validating the model with the ultimate goal of clinical translation. Second, we worked with sliding windows-based dFCs and not directly with time series. The former introduces hyperparameters that are not always easy to optimize42,43,44. In the proposed paper, we used a sliding time window of 35 TR (84 s) with sliding steps of 1 TR (2.4 s), as reported by Barttfeld and colleagues on the same dataset3. These two parameters were not optimized in our study. While a small window size may lead to increased sampling variability, a larger window size may reduce the sensitivity of the remaining analysis. In most studies, the recommended minimum was approximately 60 s2, even shorter according to recent research45. The empirical choice of Barttfeld and colleagues was within these recommendations. From a methodological point of view, working with sliding windows acts as a natural augmentation scheme that helps during the deep learning training on our limited dataset (5 monkeys—156 runs—72384 dFCs). Moreover, from a neuroscientific point of view, we aim to adhere to the dynamic representations of the brain originally described with dFCs3,4. Note that identical conclusions have been reached in humans, using a phase-based dynamic functional coordination analysis, suggesting only a small bias (if any) induced by sliding windows6. Third, tuning deep learning hyperparameters (such as learning rate or batch size) is critical to improve performance but is resource-intensive. In future work, sensitive analysis can be used to select the optimal values for each parameter using quantitative measures46. Finally, the NSM spatial preprocessing performs an affine alignment to the template space. The use of smoothing in combination with large cortical regions (as defined in the CoCoMac atlas) allows to deal with alignment inaccuracies. The resulting patterns are expected to be more robust and less sensitive to small variations in the signal.

Loss of information during compression process

This work uses VAE as a compression tool to map a high-dimensional dFC to a low-dimensional latent space. However, one of the VAE’s weak points is, in fact, its ability to reconstruct47, and so the compression process can lose a lot of information. Our benchmark quantifies precisely this loss of information, which had never been done in previous works, even those using almost the same model7,41. Our point is not to assert that the VAE chosen is the best compression tool to map a high dimensional dFC to a low dimensional latent space but to show that the loss of information, while existing, is not so great as to make the latent space uninterpretable. In the future, we could also improve the reconstruction by using a different formulation of the reconstruction term to penalize the generation of blurry images47.

Repertoire of brain patterns and arousal levels

Strikingly, the dimensional reduction with a 2D VAE could preserve the information related to each brain pattern. Furthermore, the comparison of brain patterns, using Pearson correlation similarity, clearly showed that similar brain patterns in the input space have closer latent representations (see Appendix S3, and Fig. 6-A). Looking at the last row of the correlation matrix between brain patterns, we saw that BP\({_7}\) is highly correlated with BP\({_3}\), BP\({_4}\), BP\({_5}\), and BP\({_6}\). These patterns are also direct neighbors in latent space. Conversely, the less correlated BP\({_1}\), and BP\({_2}\) are not direct neighbors of BP\({_7}\) in the latent space. Thus, the latent space can reveal the global structure of brain patterns. Moreover, the performance of brain pattern classification was better than that of arousal level classification (awake vs. anesthetized) (see Appendix S2). We observed a 0.05-point increase in classification performance. Given the difficulty of the task (i.e., a 7-class classification problem vs. a binary classification problem), the model seems to focus on the dynamic information shared between arousal levels. Similar conclusions were reached in our previous work3,4, where the brain pattern repertoire was described as a set of brain configurations that are unevenly distributed across arousal levels. In other words, compared to experimental conditions, brain patterns provide a more detailed description of states of consciousness. On the one hand, this property may be inherited from the nature of the input data. Indeed, dFCs can be directly associated with changes in consciousness over time2,4. On the other hand, the difference between levels of sedation (deep and moderate) in the present dataset is small (i.e., only a difference of one level on the monkey behavioral scale)4. Such a difference results in changes in reflexes (toe pinch, corneal reflex, shaking) but not in voluntary behavior (response to juice presentation). Therefore, establishing a direct relationship between a subject’s level of sedation and their level of consciousness may be a more difficult task than characterizing overall brain dynamics. In addition, previous studies on the same dataset have shown that all three anesthetics (propofol, sevoflurane, ketamine), despite different pharmacological molecular mechanisms, implied the same dynamics of cortical activity measured with dFCs4. Thus, it remains to be seen whether we cannot separate the different levels of consciousness because our data do not contain this information or because our modeling is inadequate.

Link between latent representations and neurobiology of consciousness

A remaining question concerns the link between these brain patterns/latent representations and the neurobiology of consciousness. Indeed, here, we studied brain dynamics using resting-state fMRI data acquired across different states of consciousness. K-means clustering could identify brain patterns that underlie the resting-state structure. Deep learning models (VAE-VIENT) could reconstruct dynamical functional connectivity maps and classify brain patterns. Low-dimensional latent representations could stratify the dynamic organization of the brain patterns and experimental conditions. Although we measured the behavioral arousal score in all experimental conditions and all monkeys, we can only speculate about the link between these representations and behavioral states. An exciting link could be provided by measuring the trajectory of brain patterns within the latent space across states of consciousness using a recently described approach48.

Generalizability of the findings to human subjects with disorders of consciousness

The advances proposed in this article are more methodological. The dimension reduction model and in silico perturbation studies could be applied to any connectivity matrix, whether from humans or animals. Given that a dynamic state repertoire associated with consciousness has also been found in humans6, the proposed results will likely be replicated, but further experiments would need to be performed. Studies in humans with dimension reduction models suggest that these models are promising for capturing the dynamics of conscious states7,41. Moreover, we previously identified a new biomarker of consciousness and its loss using dynamical fMRI approaches and structure-function similarity measures based on these exact same macaque monkey models3,4. This biomarker was directly translated to better characterize consciousness states in patients with disorders of consciousness6. Thus, although our model is developed using anesthesia-induced loss of consciousness, we are confident that it holds potential for clinical applications in improving the diagnosis of patients with disorders of consciousness.

Temporal modeling

The main limitation of the current model is its inability to explicitly model the time course of the cerebral dynamics. We worked with dynamic FC matrices but did not consider their order in each run. However, inspired by Tseng et al.49, we investigated how a 2D VAE model encoded temporal information (see Appendix S5). Remarkably, the VAE-encoded latent variables had a coherent temporal structure that exhibited transitions characteristic of consciousness, even though no constraint was imposed during training. Other important features are the time spent consecutively in each pattern (previously called lifetime), the frequency of these steady states, and the associated transitions. Interestingly, and as described in the literature3, the brain pattern closest to the structure (\(\hbox {BP}_7\)) was the most stable pattern with the longest lifetime. The latter also occupied a central place in the latent space around which other states were organized. The average lifetime of a metastable state, is lower in the awake state than in all other anesthetized states (see Appendix S5). It is also interesting to note that the distribution tails are significantly larger in the anesthetized states than in the awake state. Similarly, the number of transitions was higher in the awake state than in all other anesthetized states. Furthermore, there was almost no difference in the number of transitions between different levels of anesthesia or between different anesthetics. To interpret such results with more confidence, a time-dependent model seems essential. Some works have proposed modeling a time series with a VAE in the literature, where the encoder and decoder consisted of LSTMs50. Other works abandoned the generative property and the decoder. For example, CEBRA is a contrastive learning technique that allows label-informed time series analysis51. CEBRA jointly uses auxiliary variables and neural data in a hypothesis-driven manner to generate consistent, time-aware latent representations. In all cases, the goal remains the same: to obtain a consistent picture of the latent space that drives activity and behavior. In future work, we plan to consider the time course directly in the learning phase.

Performing virtual experiments

An interesting finding was the ability of the VAE model to simulate shifts in states of consciousness induced by selective virtual ablation of connectivity between pairs of brain areas or even ablation of connectivity within a more extended network. Historically, ablation techniques have been used in animal models to test the function of brain areas. For example, ablation techniques have directly linked vision to the occipital lobe and auditory function to the temporal lobe52,53. However, physical ablation/deactivation techniques are either irreversible or invasive and lack spatial resolution and specificity, highlighting the need for virtual ablation capabilities through the development of brain simulators54. Very few studies have been able to simulate the deactivation of global brain networks to suppress consciousness. Here, we presented a model capable of simulating a virtual experiment in which deactivation of the “macaque GNW network” leads to suppression of consciousness. But, it is not yet known whether out-of-distribution data can be accurately represented in latent spaces. However, because of this uncertainty, we explored manipulating the original data and observed what happened in the latent space. The similarity between the anesthetized brain signature and the modulated dataset signature both in latent space was certainly intriguing and reassuring. However, this raises a potential issue. The observed similarity does not rule out alternative interpretations or explanations for the brain states of anesthetized monkeys. Conversely, any differences that may arise do not necessarily indicate a failure to represent the anesthetized brain states correctly. This question requires further investigation, with more refined and improved methods in future studies, even if we believe this simulation strengthens the model’s capabilities and opens up further virtual experiments that can, for example, test the specific effects of brain stimulation on consciousness55.

Towards new biomarkers of consciousness

The 2D VAE model demonstrated its ability to retain information about regions involved in conscious processing, showing that disrupting the “GNW nodes” causes a switch from a conscious to an unconscious state. It should be noted that only virtual inactivation of the entire “GNW network” (and not inactivation of individual node-related connections or sub-networks, see Appendix S6) caused a consciousness transition. We focused on the GNW nodes for a specific reason here. We previously determined those nodes in the macaque monkey using the “local-global” auditory task34. We don’t have an equivalent for other theories nodes in the macaque monkey. However, in future work, it would be highly original to apply our new model to compare node modulation results across different theories of consciousness in the context of the current international initiative56. We can also imagine testing other networks simply by trial-and-error simulations. Setting all links connected to GNW nodes to zero is one of the limitations of the proposed ablation simulation. Setting all connections to zero is unrealistic, and perhaps certain connections should be privileged (using a weighted modulation of true connection values). We can use a more realistic perturbation scheme instead of setting all selected connections to zero in the ablation analysis. Bootstrapping techniques or model-driven approaches are possible alternatives. The latter allows the question of in silico perturbation protocols to be considered55,57. They can lead to a better understanding of the underlying mechanisms of brain dynamics. In addition, these tools can be used to test different scenarios virtually. Of course, there is still work to do to validate the realism of these scenarios. Conversely, it would be of great interest to show the opposite effect, i.e., to find the regions that should be stimulated to switch from an unconscious to a conscious state. As suggested by41, this goal is challenging and probably requires simulation. Further analysis of connection-wise RF latent space structure modeling will be valuable in this context. The RF analysis highlighted the different patterns that reflect the dynamics of the brain (biological markers). The ellipsoids obtained in our work described the most plausible connections to perturb to redirect trajectories and potentially restore wakefulness. In the long run, such an analysis may be a tool to simulate the recovery of consciousness at the individual level. Studying the sequences of different trajectories in latent space paved the way for a whole-brain computational model of conscious access. In other words, RF analysis provided the unique ability to directly identify the pairs of nodes involved in consciousness from the data. The proposed RF analysis aims to perturb a connection and observe how this perturbation affects the reconstructed dFC pattern. However, the perturbation scheme, which consists of modifying one connection at a time, needs to be refined, and the observed small effect size needs to be investigated. A first, albeit simplistic, alternative to perturbing an input connection is to sample linearly between percentiles of the connection distribution or bootstrap values across samples. Conversely, assuming our generative VAE model is properly trained, we can use the likelihood distribution of observations conditioned on the latent variable learned from the data to simulate realistic perturbations58. In reality, changing multiple connections simultaneously may have a more significant effect. Thus, navigating between states of consciousness using such a technique will require further work.

Finally, we believe numerous clinical and scientific applications exist. First, this approach allows the description of new biomarkers of consciousness. In addition, it is a unique tool to simulate the consequences of targeted modulation of specific brain regions for the loss or recovery of consciousness. In this context, we hypothesize that the latent space structure will be essential for dissecting the mechanisms of Deep Brain Stimulation (DBS) for disorders of consciousness and help to build a general predictive model of the global brain effects of DBS.