Introduction

This study was aimed at developing a new method to improve the study of fragmented flint elements, particularly those with laminar (blade) blanks, through a machine learning approach, specifically a feedforward neural network analysis created in a multi-paradigm programming language and numeric computing environment. Our proposed method may enable a better understanding of the lithic technologies used, and the cultural choices made, by Middle Pre-Pottery Neolithic B (MPPNB) communities, such as those in the Southern Levant. The current analysis was carried out exclusively on laminar artefacts made of flint, as it is the main raw material used for chipped stone artifacts in the Southern Levant. Nevertheless, the following methodology can be applied to other raw materials, such as obsidian (a common raw material used mainly in the Northern Levant and parts of Turkey).

Throughout the Neolithic period in the Levant, and specifically during the cultural koiné of the MPPNB (10,200/100–9,500/400 cal B.P.), laminar blanks were a major target of lithic production that enabled shaping formal tools by retouching blades1,2,3,4). The tool repertoire in both the Northern and Southern Levant often includes sickle blades, arrowheads, knives, perforators, truncated elements, notches, and denticulates5,6,7.

The production of blanks is therefore fundamental for understanding the cultural choices or preferences of the community, specifically those of the flint knappers during tool production.

However, tool retouching, wear, and re-use for shaping other tools hinder accurate determination of the genuine metric preferences. The process of retouching, in particular differences in the invasiveness of retouch by tool types (e.g. sickle blade, arrowhead, etc..) and by chrono-cultural affinity (Neolithic of the Levant, of the Maghreb, of Eastern Mesopotamia, etc..). The modification along the edges may differ from few millimetres in case of a marginal retouch, to a significant change of the tool’s surface itself in case of a covering retouch8,9. Additionally, post-depositional processes frequently compromise the preservation of laminar blanks, thereby restricting understanding of the complete scope of flint production10.

Here, we present a method for reconstructing the original metrics of each item in every assemblage with high accuracy, thus broadening archaeological perspectives regarding cultural choices related to selection preferences along the metric range. More broadly, this method deepens understanding of the laminar trajectory in the MPPNB context, in which laminar production is of paramount importance, and blades are the main blanks used for formal tools, such as sickle blades and arrowheads. Blades are indeed the main blank used for tools production in many sites across the Levant. As a matter of fact, laminar blanks often represent many of the tools assemblage in Neolithic Levantine contexts throughout the Pre-Pottery Neolithic period, such as at Akarcay Tepe phases I-VI11, Mureybet phases IV12, Abu Gosh layers III-IV13, Ashkelon layer IV14, Beisamoun Layer I-III15,16 (Bladelet production is a conspicuous trajectory at this site and it uses a different technology rather than the bidirectional technology characteristic of the PPNB17.), Er-Rahib18 and more19,20. Of note, this study highlights the fact that the studied laminar trajectory relates to blade production rather than bladelet production (At Kaletepe, for example, bidirectional laminar reduction is also applied to a bladelet series production21. Interestingly, in the PPNC (e.g., Beisamoun, Ain Ghazal), when the use of bidirectional blade production decreased or was absent, bladelet production appeared as a clear production trajectory15,22.). Based on the analysis, most of the laminar blanks that were examined are actually blades. The selected sites exhibit the same trend. The Nahal Yarmouth sample shows 68.4% blades and 31.6% bladelets, the Motza sample shows 80.6% blades and 19.4% bladelets, the Yiftahel sample shows 66.1% blades and 33.9% bladelets, and the Nahal Reuel sample shows 60.6% blades and 39.4% bladelets.

Finally, our method highlights and confirms the existence of shared trends in laminar production, despite some variability within the MPPNB period, and the different environmental settings of the sites, i.e., the Mediterranean and desertic phytogeographical ecozones of the southern Levant. Furthermore, the results of this analysis support the potential standardization of metrics in laminar production across the Southern Levant.

The results of this study indicated the promising accuracy and efficacy of machine learning in predicting artifacts’ metrics, and potentially also indicating cultural preferences, such as flint selection and/or laminar blank functionality (e.g., sickle blades or sickle fragments without retouch). The artifacts’ metrics also relate to the potential final typological shape/morphology after the retouching process (e.g., sickle blades or sickle fragments with retouch). Finally, this method can produce data sets for further comparisons within similar (chrono-cultural and technological chaîne opératoires/chains of operation) contexts at sites with few or absent undamaged artifacts. We propose that our method can overcome the lack of data even in cases involving a set of solely fragmented artifacts.

Materials and methods

Site selection was based primarily on the assignment of the four sites to the MPPNB and their cultural affinities reflected in material culture elements, particularly lithic technology. A major technological trait of Pre-Pottery Neolithic B (PPNB) sites, specifically MPPNB sites, is the reduction of selected raw materials, mainly flint, to produce laminar blanks for shaping tools used in daily life activities. The Levantine laminar technology tradition, which is characterized by the production of stone tool blanks through the systematic removal of blades/bladelets from a prepared core, has its origins in the Upper Palaeolithic period, although based on different core reduction technologies23,24. This tradition continued to develop and flourish throughout the subsequent Epi-Paleolithic period, throughout which laminar reduction was mostly aimed at bladelet production25,26,27,28. During the Pre-Pottery A period, a blade reduction technology was evident, while bladelet production continued to a certain degree29,30,31,32,33,34. Blade reduction eventually became the dominant technological trajectory for producing tool blanks during the PPNB in the region.

Beyond similarities in material culture, Southern Levantine MPPNB sites vary. In the case presented here, whereas Nahal Yarmuth 38, Motza, and Yiftahel are open air sites in Central and Northern Israel, in the Mediterranean zone rich in highly diverse resources with a subsistence economy comprising domestic crops, Nahal Reuel is instead a small site in a hyper-arid zone in Southern Israel with an economy based on hunting-gathering and no domesticates. As a marginal desert site, Nahal Reuel also shows a lithic typology, which slightly diverges from that of typical MPPNB Mediterranean sites (e.g., a lack of woodworking tools [bifacial tools] and sickle blades).

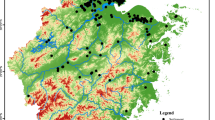
The selection of archaeological artifacts from each of the studied sites (Fig. 1) was performed by a random-stratified sampling method35,36,37,38 allowing all technological and typological categories to be retained within the lithic assemblages of each site. This sampling methodology therefore allowed a selection of both unidirectional and bidirectional laminar blanks, central and lateral (according to the technological laminar subcategories provided by5). The method allowed the selection of distal or proximal fragmented laminar blanks, as well as undamaged artifacts. The selection was made of high reliability loci unaffected by earlier or later phases of occupation nor by modern activities.

Fig. 1
figure 1

Selection of studied laminar artifacts from Motza (a-e),Nahal Yarmuth 38 (f-j), Nahal Reuel (k-n), and Yiftahel (o-s).

Full size image

The site of Nahal Yarmuth 38 is located 220 m above sea level, 34 km east of the Mediterranean coast and 30 km west of Jerusalem. Extensive excavations recently exposed an area of 700 sqm with structures and typical MPPNB material culture. Unlike the villages of Motza and Yiftahel, Nahal Yarmuth was a smaller site, characterized by a high number of primary human burials and scarce evidence of active residential practice, that might classify it as a burial site39,40). No C14 dates are available yet.

The site of Motza is situated 600 m above sea level, 5 km west of Jerusalem, in the Judean hills, and was discovered and described in the 1920s. Several archaeological campaigns have been performed in recent years, including major large-scale work in the late 2010s. The site shows a full PPNB sequence, from the Early PPNB to the Final PPNB (PPNC) and is one of the largest open-air sites of the PPNB period in the entire Levant.

The Early PPNB of Motza is dated 10,400–10,200 cal. BP, the Middle PPNB phase is dated 10,100–9,300 cal. BP, and the Final PPNB phase is dated 9,000–8,700 cal. BP41.

The MPPNB at Motza comprises a typical architecture with rectangular floor plan buildings, with floors covered by high quality lime plaster, and primary or secondary burials found in association with houses’ floors41.

The Motza sample was from area B, assigned to the Middle-Final PPNB phases, specifically from area B-10, where a rectangular domestic structure from the MPPNB has been exposed42. The structure is ~ 150 sq m in area and is composed of four rectangular rooms with three construction phases. The selected lithic sample came from the first and second phases, to avoid any later contexts or materials.

The open site of Yiftahel is located on the banks of Nahal (river) Yiftahel in the Lower Galilee, next to Nazareth, within a typical Mediterranean zone (like Motza). The site was first excavated in the 1980s and was subsequently excavated in 2009. The MPPNB layer of the site was dated to 10,200–9,600 cal. BP. The sample presented here is from the PPNB layer in Area E, Squares E20–E23 and F20–F22, which belong to layers C2 and C3, the deepest MPPNB layers from stratum IV of area E. This area shows domestic, rectangular, internally subdivided structures (with in situ groundstone tools and animal remains), chipping areas, and open areas43,44.

The site of Nahal Reuel is located in the Uvda valley in the Southern Negev. Unlike the previous sites, it is located in a typical desertic environment, with a maximum of 50 mm modern annual rainfall within a Saharo-Syndian vegetation zone. The site was salvage excavated in 1980–1981, thus highlighting a MPPNB occupation with rounded, internally sub-divided structures whose floors indicate daily activities and installations such as fireplaces. Next to the residential area, an unearthed open space contains knapping workshops, pits, and possible storage installations (potentially silos) indicating various daily outdoor activities45,46.

The sample from Nahal Reuel includes domestic structures (I, II, and IV) and open areas (IX, and XII), as well as knapping areas (III and X)45.

We studied laminar items produced primarily by bidirectional reduction technologies and secondarily by unidirectional reduction, representing the middle-late stage of the chaîne opératoire that leads to tools production (We don’t discuss the early stages of the reduction process, including raw material acquisition and selection, early core preparation, etc.). These laminar-technological trajectories are clearly visible in the débitage (on the basis of the direction of previous detachments on the dorsal side and their chronological sequence of detachments) and the core characteristics. Cores play important roles in defining and highlighting the reduction sequences and their various modalities. These cores include bidirectional blade cores (including the well-known naviform cores), which are an important component of the MPPNB reduction processes that enabled standardized production of flat (non-twisted) and straight (non-curved) laminar blanks. Most of the cores associated with the sampled laminar blanks used for this study were indeed quite exhausted, which confirms a high degree of reduction in blades production.

Bidirectional technologies were largely used to produce laminal blanks for shaping formal tools, such as sickle blades, arrowheads, perforators, burins, and end-scrapers, and for shaping informal tools based on truncated elements, notches, and denticulates. Unidirectional blade production is also present but is not central to any MPPNB assemblages.

The bidirectional laminar technology is considered a material culture “fossil guide” for the MPPNB throughout the Levant, from Southeastern Anatolia to the Sinai Peninsula, and from the Mediterranean coasts to the desertic areas of Syria and Jordan, an area covering more than 800.000 sq km. The use of a generally similar technology of reduction across such a large region with diverse environments enables the entire area to be statistically treated as a whole, from an archaeological (cultural) viewpoint, thus allowing potential differences to be traced across phytogeographical zones7,47,48).

From a purely technological standpoint, the blade production of sites located in desert ecosystems does not substantially differ from that at sites in the Mediterranean zone. In fact, these laminar technologies are based on the same underlying principles of tandardized bidirectional production, and with the same structural logic. Nonetheless, technological nuances may differ across regions and between sites, given their varying socio-economic and environmental contexts. These nuances affect (to a certain degree) the technological spectrum as well as the typological repertoire. Settled sites in the Negev desert, such as Nahal Issaron49, Nahal Reuel, or the Jordanian Wadi Rum50 (e.g., Ayn Abū Nukhayla), often lack (or show extreme rarity) of certain elements, such as wood-working stone tools or sickle elements (Consequently, the re-use of elements such as sickle blades, for example at Motza and other MPPNB sites, is not relevant to these sites that lack sickle blades.).

Consequently, a variability study was performed to confirm the technological similarities observed among these sites, despite the differences in their regional environments. The technological process of reducing blades exhibited consistent patterns, and produced non-twisted, non-curved blades. Therefore, laminar blanks were selected for this study. Laminar blanks are a highly standardized component within the débitage, compared to flakes or core trimming elements. Laminar artifacts best reflect the standardization process in lithic production during the Levantine Neolithic, particularly the MPPNB18. The relatively low metric variability observed in laminar products as observed in an initial analysis of metrics correlations and standard deviations of the sampled laminar blanks, and the highly standardized production based primarily on bidirectional reduction (and secondarily on unidirectional reduction), provide an opportunity to analyse and predict the fragmented blades and bladelets’ original metrics spectrum. In contrast, such an analysis would not be feasible for the tools category, because these were shaped by diverse retouching techniques that can heavily change their original metrics. However, this possibility would be achievable by incorporating more metrics that refer to the tools’ characteristics. Furthermore, the selection of laminar artifacts included both blades and bladelets as part of the same technological category. Both these sub-categories were indeed part of the same flint cores’ reduction process that was based on blade production. A deeper explanation of the specific distinction between blades and bladelets made in this study is necessary to avoid any misunderstanding from an archaeological perspective. We chose to maintain the conventional distinction between these two categories, on the basis of a metric viewpoint only: bladelets were considered laminar products whose length was shorter than 50 mm and whose mesial width was less than 12 mm while blades are larger4. This distinction is maintained in the text that follows. This distinction is purely dimensional/metric, but from an archaeological and engineering point of view it was not necessary to process these sub-categories separately or differently,in fact, bladelets were exclusively the products of the same core reduction investigated, and not a separate trajectory of lithic productions. Thus, blades and bladelets were processed together in the neural network analysis (see below), but their original and predicted metrics are shown separately.

Every complete artifact was measured as follows. The maximum length represented the longitudinal axis from the butt to the tip. The width and the thickness were the axes perpendicular to the length, and were measured halfway along the length, and also between the end of the bulb and the mesial part, and between the mesial part and the beginning of the distal end. Fragmented artifacts were measured according to their state of conservation. We focused on reconstructing artifacts that preserved either the proximal and mesial parts, or the mesial and distal parts. This rapid measurement system enabled neural network analysis to be performed on regular artifacts, respecting the technology of their production, thus enabling comparison among individual artifacts while minimizing human errors in the analysis.

A Bayesian regularization back-propagation algorithm was utilized to conduct a neural network analysis, incorporating the available data. Among several available algorithms, the Bayesian regularization back-propagation algorithm represented the best choice in terms of efficiency and results. Previous efforts to predict metrics for regular artifacts (The term “regular artifacts” refers to a metric regularity of artifacts, where metric variability is usually low.) utilized a linear regression approach, although focusing on fewer variables (Goldestein, 2014). However, we suggest a more advanced approach employing a neural network and a Bayesian regularization back-propagation algorithm, in conjunction with a measuring system incorporating seven variables (see Fig. 2), provides a more precise calculation of missing metrics. Furthermore, a comparative analysis was conducted to select the most efficient algorithm between the Levemberg-Marquardt training algorithm and the Bayesian regularization back-propagation algorithm, and the results highlighted the superior efficiency and performance of the Bayesian algorithm51.

Fig. 2
figure 2

Technological measurements51.

Full size image

For these reasons, it was chosen to conduct the following analysis.

Neural network, and in a broader sense machine and deep learning analyses, have been widely used for various purposes e.g., radar/satellite images elaboration for sites detection and their architectural subdivisions has been an extensively studied area.

Different approaches, including fuzzy and Bayesian techniques, have been employed to effectively process and interpret the data using neural networks. These techniques have proven to be highly effective in discerning patterns and trends that may not be immediately apparent to the human observer. For this reason, they are often combined with other methodologies, such as lidar ((Laser Imaging Detection and Ranging) to improve archaeological topography. These combined techniques have allowed for the detection of architectural remains (archaeological sites or part of them) from different periods and regions52,53,54,55.

In recent years, neural networks have been used in several ways, combining different approaches. Recently they have been combined with spectroscopy-based techniques for artifact typological classifications based on morphometric parameters for the study of pottery and human skeletal remains. This approach has shown promising results and has been adopted to enhance the accuracy of classification. The use of neural networks in conjunction with spectroscopy-based techniques has enabled artifact classifications that were previously difficult or impossible to achieve.

Machine learning and AI have been applied in various ways to optimize performance in the analysis of use-wear on lithic artifacts. These technologies have been utilized to enhance the understanding of how stone tools were used in the past, providing valuable insights into ancient human behavior and activities. These techniques have expanded the horizons of artifact classification and the recognition of use-wear patterns and improved our understanding of the past56,57,58,59.

To achieve our goal of gaining deeper insights into complex data patterns, we have carefully selected a sophisticated machine-learning technique based on neural network analysis. In order to ensure robustness and accuracy, we have chosen to use a Bayesian approach, which allows us to incorporate prior knowledge and uncertainty into our analysis. This approach enabled us to make informed decisions and generate reliable predictions of laminar blanks’ metrics, The main target of this study was indeed to create a method that was able to predict the original metrics of fragmented regular artifacts, such as blades and bladelets produced during the Middle Pre-Pottery B in the Levant.

The method used to measure the dimensions of each artifact involved measuring the maximum length, width, and thickness. The ‘technological length’ represents the line that connects the striking platform to extremity of the distal end (Fig. 2: a-b); the ‘technological mesial width’ is the width measured at half of the length of the artifact (Fig. 2: e–f); the ‘technological mesial thickness’ is instead the thickness measured at half of the length of the artifact (Fig. 2: e1-f1). Furthermore, measurements of thickness and width were taken at specific positions based on the technological characteristics of lithic artifacts. These positions are identified by the location of the proximal and distal ends. Measurements of width and thickness, therefore, were taken along the line separating the proximal end and the medial part (Fig. 2: c-d and c1-d1) as well as the line separating the medial part and the distal end (Fig. 2: g-h and g1-h1). This approach allowed us to gather comprehensive information not only on complete artifacts but also on fragmented ones.

A Bayesian regularization back-propagation training algorithm for neural network analysis was therefore selected for its efficacy and ability to limit overfitting problems. In the Bayesian regularization back-propagation training algorithm implemented in MatLab the validation stop is disabled due to a built-in regularization process60. The validation stop value (max_fail) set differently from zero may affect the algorithm performance. Usually, long training periods are in fact required to obtain a neural network able to generalize properly, while an early stopping system may affect its capability. However, using the validation stop as a regularization method in this algorithm led to a performance improvement of the neural network analysis of the studied datasets.

Several steps were developed. First, a feedforward neural network was created with two hidden layers: one composed of 80 perceptrons and one composed of 120 perceptrons. The input layer therefore consisted of four perceptrons, as many as the known variables for every single artifact; two hidden layers; and one output layer represented by three perceptrons, as many as the number of unknown variables, comprising missing metric information to be predicted by the neural network (Fig. 3). The feedforward architecture was selected as the most effective structure able to deal with non-linear regression data in a small dataset. Other algorithms, such as the Levenberg–Marquardt training algorithm, or other neural network structures, such as the “super vector machine” (SVM) are not able to process this small dataset. The creation of a neural network that is able to work in a small dataset, avoiding underfitting and overfitting problems was indeed one of the aims of this study, which is why we decided to select this specific architecture.

Fig. 3
figure 3

Example of the perceptron mechanism in a feedforward neural network.

Full size image

Successively, the activation functions of the perceptrons were selected. One activation function corresponded to the hyperbolic tangent and was meant to be used for the hidden layers, and the other activation function corresponded to a linear function and was meant to be used for the last output layer. The choice of activation functions for the neural network layers is crucial because it affects the network’s ability to learn and represent complex data relationships. The hidden layer activation function was the hyperbolic tangent function, which is commonly used in neural network studies to introduce non-linearities. A linear function was instead used for the output layer (Fig. 4). Finally, for neural network learning, a database of exclusively complete and undamaged artifacts was used.

Fig. 4
figure 4

Example neural network layer mechanism.

Full size image

Furthermore, the Bayesian Regularization algorithm was used for learning the neural network. Because of the small amount of data used for the network learning, the algorithm showed an overfitting problem. Overfitting occurs when a complex model, such as a neural network, adapts very well to training data but fails to properly generalize data not included during the training process. Consequently, low performance on new data and a loss of model prediction capability may be observed.

Consider a neural network with a training dataset B containing b_t pairs of input and target vectors in the network model, i.e.:

$${\text{B }} = \, \left\{ {\left( {{\text{x}}\_{1},{\text{ y}}\_{1}} \right), \, \left( {{\text{x}}\_{2},{\text{ y}}\_{2}} \right), \, \ldots , \, \left( {{\text{x}}\_\left( {{\text{b}}\_{\text{t}}} \right),{\text{ y}}\_ \, \left( {{\text{b}}\_{\text{t}}} \right)} \right)} \right\}$$

The goal of the neural network is to learn a function that maps the input vectors to the corresponding target vectors. During the training process, the neural network tries to approximate this function by optimizing its weights on the basis of the training data.

The Bayesian Regularization algorithm uses the weight distribution a posteriori to find a balance between the adaptation to the training data and the weight regularization. In this way, the algorithm creates a solution that generalizes better over new data, thereby decreasing the overfitting risk. The use of Bayesian Regularization in updating the neural network weights enables more stable models and decreases the dependency on time-consuming and expensive cross-validation techniques. This algorithm combines both training data information and weight information a priori to obtain a more accurate valuation of the optimal network weights.

The algorithm is based on the idea of applying penalization to the cost function of the neural network to avoid excessive adaptation to training data (overfitting). This system is based on the network weights’ distribution a priori.

The learning machine’s algorithm is interrupted when a stable network condition is reached. The training is interrupted, and the net is generated on the basis of the obtained weights for which the error is minimal.

The evolution of the training and the validation errors over the epochs can provide information on the convergence of the training. Ideally, both the training and validation errors must decrease over time and stabilize. If the training error continues to decrease as the validation error increases or stabilizes, overfitting might have occurred, such that the neural network has learned to store training data without good generalization of new data.

Furthermore, the training graphs show where the training is interrupted, as indicated by the specified interruption criteria, such as when the neural network weight gradient value falls below the specified threshold or when the training error reaches or falls below the specified value. This point can be highlighted in the graph or indicated by a vertical line or label. In summary, training can be interrupted when the error reaches a minimum value (goal) or when the gradient value falls below a threshold. Both criteria can be used to determine the end of training, depending on the settings, specifically the number of perceptrons used.

The interpretation of the graphs is focused on the trends in the training and validation errors within the epochs’ evolution. An attempt is made to determine whether the error progressively decreases or stabilizes at a certain point. Subsequently, both the training and validation errors are compared to verify their similarities or differences. Attention should always be paid to training breakpoints, if any, to understand when and why the training has stopped.

Finally, the goal of the training process is to find optimal values for neural network weights such that the network can produce accurate outputs for new inputs that were not presented during training.

Analysis

An initial analysis was performed on the lengths of the complete laminar blanks to highlight the metric variability of the maximum technological length and to verify the metric variability among sites (Fig. 5). To do so, we subdivided the artifacts into ten length ranges (The length ranges were as follows: group 1, 0–20 mm; group 2, 20.1–30 mm; group 3, 30.1–40 mm; group 4, 40.1–50 mm; group 5, 50.1–60 mm; group 6, 60.1–70 mm; group 7, 70.1–80 mm; group 8, 80.1–90 mm; group 9, 90.1–100 mm; group 10, > 100 mm. The subdivision’s nature was arbitrary to simplify the laminar metrics variability’s understanding.).

Fig. 5
figure 5

Length variability of intact laminar blanks from the selected samples.

Full size image

The subdivision showed a high variability from all the sites, with the unique exception of Motza, where the length range is narrower. The technological length range of the undamaged laminar blanks from Nahal Yarmuth was mostly represented by the third group, nevertheless the range included both bladelets’ and large blades’ groups 1 and 10. The technological lengths of the intact laminar blanks from Motza showed a narrower range of metric variability. Motza’s sample was best represented primarily by group 8 and secondarily by group 3, whereas Yiftahel’s sample was best represented by groups 7 and 1. The technological length of the intact laminar blanks from Nahal Reuel was represented by a wider metric range including both the first and last groups.

The differences in metric variability, particularly among regions, did not impede deeper analysis.

The selection of the artifacts, specifically laminar blanks, was based on their low coefficient of variability (C.V.), and high correlation rate, showing good proportionality values among metrics (Table 1). The concepts correlation and coefficient of variation are essential statistical tools for gaining insight into the variability of metrics. Correlation evaluates the level of interdependence between two variables, indicating a predictive relationship between them. In this context, high correlations are observed between the length and width, and the length and thickness. The strong dependency between these variables can be attributed to the consistent nature of these artifacts and the defined metrics of laminar artifacts, whether they are blades or bladelets. On the other hand, the coefficient of variation gauges the dispersion of a probability distribution. It is a measure of the ratio of the standard deviation to the mean, providing valuable insight for comparing variation across different data series.

Table 1 Variability indexes of undamaged artifacts.
Full size table

In the context of standardized laminar artifacts and proceeding with metric prediction analysis, it is insightful to initially compare the coefficient of variation values of laminar blanks’ metrics to the undamaged flake products from the same site’s samples subjected to the same sampling methodology. The findings reveal a significantly lower variability between the length and width, and the length and thickness among laminar blanks compared to flakes.

However, this initial analysis not only underscores the inter-variability between laminar blanks and flake products within each site, but also highlights intra-variability among the metrics. It is evident that the most consistent metrics are represented by the length-to-width ratio among laminar artifacts, while the length-to-thickness ratio exhibits greater variability. Nonetheless, the coefficient of variation for the metrics of flakes demonstrates noteworthy variability in both ratios, particularly the length-to-width ratio.

It is important to note that the laminar artifacts (produced by bidirectional technology) fall under different sub-categories5. These subdivisions, primarily regarding central or lateral blades, encompass various types of laminar detachments based on their position on the core’s surface, as well as two distinct laminar technologies (i.e., unidirectional and bidirectional technological trajectories). This distinction holds significance as it suggests that the diversity in artifact metrics arises not only from the reduction in core size but also from the type of laminar detachment and technology employed. Therefore, the variability index must be interpreted within the inherent variability existing within the laminar artifact categories. As a consequence, We observed difference in the coefficient of variation between laminar and flake artifacts and this gains a deeper meaning, supporting the idea of a high standardization and regularity of laminar artifacts that allows the metrics prediction analysis.

The dimension of laminar artifacts appears to be independent of the flint sources, as there is a consistent preference for a range of dimensions. Although the presence of larger cores due to crops/sources or nodules in the areas could yield bigger laminar blanks, the dimension spectrum remains consistent across all sites, suggesting a knappers’ choice.At each site, the regularity of artifacts showed a metric proportionality highlighted by the linear regression obtained from the length/width ratio and the width/thickness ratio (Fig. 6). As shown in the graphs, these preliminary results indicated high standardization of artifacts’ metrics, thus suggesting that these artifacts are an ideal element for metric reconstruction of fragmented laminar artifacts through neural network analysis.

Fig. 6
figure 6

Linear regression curves of complete laminar artifacts from Motza (a, b), Yiftahel (c, d), Nahal Reuel (e, f), and Nahal Yarmuth 38 (g, h) based on the length/width ratio (a, c, e, g) and length/thickness ratio (b, d, f, h).

Full size image

The first step in neural network analysis is the training process. Among undamaged artifacts from the studied sites, a total of 234 laminar blanks (18.8% Nahal Yarmuth, 17% from Motza, 22.2% from Yiftahel, and 41.8% from Nahal Reuel) were used (Supplementary Material Table 1). The metric analysis of the different sites indicated size homogeneity of the blanks, including both blades and bladelets, thus indicating the same cultural choice in this region (Table 2). It is notable the presence of a few elements, such as large blades and micro-bladelets, that affected the maximum and minimum values, nevertheless, most of the artifacts are dimensionally homogeneous.

Table 2 Metric analysis of undamaged artifacts. Metrics are expressed in mm.
Full size table

Moreover, the analysis of the average metrics showed the same results, indicating low variability. The only notable difference was that the average length was 10 mm shorter in blades from Motza, and 7 mm shorter in blades from Nahal Yarmuth 38, than those of blades from both Yiftahel and Nahal Reuel. The analysis of bladelets variability showed imperceptible differences (Table 3).

Table 3 Metric analysis of the undamaged artifacts (average). Metrics are expressed in mm.
Full size table

The analysis indicated successful training and validation of the database consisting solely of undamaged artifacts without conservation of either the distal or the proximal end (Supplementary Material Table 2). A total of 70% of the undamaged artifacts in each reconstruction were used for the training process, and the remaining 30% were used for error calculation. Furthermore, the algorithm divided the 70% into three sets: one for the proper training process, one for the data validation, and one for the final test. In both the training and validation processes, the selection was random, with no experimenter decisions or interference that might have affected the results.

To confirm the validity of the internal training process made on 70% of the artifacts, and to calculate its error, a best validation performance test was performed on the data training, validation, and test (Fig. 7).

Fig. 7
figure 7

Best validation performance for metrics prediction of artifacts with missing proximal end.

Full size image

The validation error was calculated with a separate data set that was not used for neural network training, thus enabling independent measurement of the predictive ability of the neural network. The goal was to keep the validation error low and similar to the training error.

The evolution of the training error and validation error over the epochs provides information on the convergence of the training. Ideally, the training error and validation error should decrease over time and stabilize at some point. If the training error continues to decrease as the validation error increases or stabilizes, overfitting might have occurred, and the neural network might have learned to store training data without generalizing well over new data.

Training graphs may also show where the training was interrupted, as indicated by the interruption criteria specified, such as when the neural network weight gradient value falls below the specified threshold, or the training error reaches or falls below a specified value. This point can be highlighted in the graph or indicated by a vertical line or label.

For interpretation of the graphs, the evolution of the training error and validation error over the epochs is observed. An attempt is made to determine whether the error progressively decreases and stabilizes at a certain point. The training and validation errors are compared to verify whether they are similar or slightly different. Attention should always be paid to training breakpoints, if any, to understand when and why the training has stopped.

The best validation performance of the artifacts with missing proximal ends was 45.1844 at epoch 28, thus indicating that the lowest error during the validation process was obtained at that epoch.

In the reconstruction of the artifacts without a preserved proximal end, the error calculated in the three metrics (length, width, and thickness) was low in the training and validation processes (Fig. 8).

Fig. 8
figure 8

Error histogram during training, validation, and test for metrics prediction of artifacts with missing proximal end.

Full size image

The histogram graph (The histogram shows the modalities in which errors are distributed within different ranges, indicating whether the distribution is centred around a specific value or is more spread. A more concentrated distribution around low values indicates that training is progressing well, whereas a wider distribution may suggest difficulties in the training process.) should be a bell-shaped curve, centered as close to the value of 0 as possible. This graph indeed showed good results. To confirm the quality and efficiency of the neural network, the linear regression values of the training process must be determined.

The analysis (The graph shows training, validation, and test errors. Ideally, the training and validation errors should be low and similar) indicated that the results yielded predicted values close to the ideal values (dotted lines) in the proper training, validation, and test processes (Fig. 9). This proximity of the data to the ideal line indicated that the training process was conducted successfully, and neither underfitting nor overfitting affected the analysis.

Fig. 9
figure 9

Training process for prediction of artifacts missing the proximal end. Training, validation process, internal test, and combination of the previous graphs.

Full size image

The correlation coefficient (R) (R values between 0 and 1 indicate the lowest and highest correlation possible, respectively.) between the predicted and real values was extremely high in the training, validation, and test: 0.93 in the training and validation processes, and 0.95 in the test.

Moreover, the lines indicated the extent to which the predicted data approached the real ones during the training of the neural network. Lines are closer to the ideal line if the network is correctly learning. Ideally, three linear regression training tests are superimposed with the ideal linear regression. This goal is difficult to achieve because if the predicted data are identical to the real data in the training phase, all points would be aligned on the regression line. This result, unfortunately, would involve overfitting of the neural network, and the regression lines of the validation and test would be very distant from the ideal lines because the network does not generalize over all values ever submitted. The regression graphs showed the trend of the validation and test lines, and the achieved regression lines were therefore acceptable for the metrics prediction of artifacts with missing proximal end.

The accuracy of the three predicted metrics was high (Table 4), and the results were coherent with the aforementioned real values of the undamaged artifacts’ metrics. The comparison between the undamaged artifacts metrics and the prediction of artifacts with missing proximal ends’ metrics, showed that the closest results were represented by the bladelets category and by the minimum values of the blades’ category, while the blade’s maximum values were affected by the presence of a few large blades. To avoid such misleading results, we therefore decided to calculate the average of these artifacts metrics.

Table 4 Metric analysis of the predictions for artifacts with missing proximal ends. Metrics are expressed in mm.
Full size table

The results of the predicted average blades’ metrics did not diverge from the real artifacts’ average metrics (Table 5). The good quality of the prediction was indeed confirmed by these results.

Table 5 Metric analysis of the average predictions for artifacts with missing proximal ends. Metrics are expressed in mm.
Full size table

Furthermore, an additional test was made separately to calculate the error both on 70% of the data (data training prediction) and on the remaining 30% of artifacts (final test prediction). The training error was 24.3% for the length, 10.4% for the width, and 31.9% for the thickness; therefore, the minimum accuracy of the analysis was 75.7%, 89.6%, and 68.1%, respectively (Fig. 10).

Fig. 10
figure 10

Data training prediction. Test carried out on 70% data. The test was carried out on metrics prediction of artifacts with missing proximal end.

Full size image

The final test error was 23.2% for the length, 10.8% for the width, and 26.4% for the thickness, and the accuracy was 76.8%, 89.2%, and 73.6%, respectively (Fig. 11).

Fig. 11
figure 11

Final test data prediction. Test carried out separately on 30% of artifacts. The test was carried out on metrics prediction of artifacts with missing proximal end.

Full size image

In the prediction for artifacts with missing distal ends (Supplementary Material Table 3), we performed the same procedure used for the metric prediction of artifacts with missing proximal end.

First a best validation performance test was carried out (Fig. 12). The best validation performance test was 67.7759 at epoch 26, with no better results after 46 epochs.

Fig. 12
figure 12

Best validation performance for metrics prediction of artifacts with missing distal end.

Full size image

The training, validation, and test processes all showed low error values, as demonstrated by the error histogram (Fig. 13).

A good definition of the values was qualitatively showed by the histogram’s bell shape6 and clustering of most of the results near 0.

Fig. 13
figure 13

Error histogram during training, validation, and test for metrics prediction of artifacts with missing distal end.

Full size image

Furthermore, additional validation and support regarding the efficacy and efficiency of the neural network was indicated by the linear regression lines calculated during the training, validation, and test processes (Fig. 14). In each case, the predicted values were close to the ideal line; moreover, the correlation value was set on 0.94 during the training and validation process, and 0.96 during the final test, thus confirming the efficacy of the analysis.

Fig. 14
figure 14

Training process for prediction of artifacts missing the distal end. Training, validation process, internal test, and combination of the previous graphs.

Full size image

As for the metrics prediction of artifacts with missing proximal ends, the linear regression lines achieved during the training showed good results. In both cases indeed, the regressions were not affected by overfitting problems.

The analysis indicated that the predictions had high accuracy and were in line with the real metrics of the undamaged artifacts (Table 6). The differences were not significant within both the blade and bladelet categories. For a better understating and in order to avoid misleading results due to the presence of large blades in the undamaged artifacts dataset, we decided to show the results of the analysis based on the metrics average.

Table 6 Metric analysis of the predictions for artifacts with missing distal ends. Metrics are expressed in mm.
Full size table

Therefore, the average of the metrics of artifacts with distal missing ends did not diverge from the average of undamaged artifacts metrics (Table 7). The results were indeed homogeneous and coherent with the real values.

Table 7 Metric analysis of the average predictions for artifacts with missing distal ends. Metrics are expressed in mm.
Full size table

Furthermore, an additional test was made separately to calculate the error both on 70% of the data (data training prediction) and on the remaining 30% of artifacts (final test prediction). During the training process, the error for the three predicted metrics was 21.7% for the length, 19.8% for the width, and 24.7% for the thickness; consequently, the accuracy was 78.8%, 80.2%, and 75.3%, respectively (Fig. 15).

Fig. 15
figure 15

Data training prediction. Test carried out on 70% data. The test was carried out on metrics prediction of artifacts with missing distal ends.

Full size image

During the final test prediction, the error for the three predicted metrics was low as well, at 28.4% for the length, 14.1% for the width, and 26.8 for the thickness, thus indicating an accuracy of 71.6%, 85.9%, and 73.2%, respectively (Fig. 16).

Fig. 16
figure 16

Final test prediction. Test was carried out separately on 30% of artifacts. The test was carried out on metrics prediction of artifacts with missing distal ends.

Full size image

Lastly, an important step was the comparison between the original dataset of laminar blanks and the final dataset after the metric prediction. While the technological subdivision between blades and bladelets for damaged laminar artifacts is based on visible and preserved metrics, it may not always be accurate. Upon further examination, it became clear that the ratio between blades and bladelets had undergone a minimal quantitative alteration (Fig. 17).

Fig. 17
figure 17

Comparison of laminar artifacts’ composition. On the left is the composition before the metrics prediction analysis. On the right is the composition after the metric prediction analysis.

Full size image

In this study, the initial dataset of laminar artifacts used for the metric prediction analysis consisted of 75.6% blades and 24.4% bladelets. After the analysis, there was a slight change in the proportion of blades and bladelets, with 72.8% being blades and 27.1% being bladelets. This change was mainly observed in the artifacts from Nahal Reuel.

Discussion

This study was aimed at gaining a better understanding of standardized lithic technologies for blade production during the MPPNB (mostly 8th millennium cal BC) in the Southern Levant. The new methodological tool presented here may:

  • enable prediction/reconstruction of the original metrics of standardized artifacts;

  • allow comparisons between different sites/assemblages sharing the same technological system;

  • and, highlight cultural affinities of the analyzed assemblages/sites.

Furthermore, the artificial intelligence (machine learning) method used here is accessible to all those interested, owing to its (available and simple) multi-paradigm programming language and numeric computing environment. Moreover, its parameters can be rapidly measured based on the technological features shared by the examined lithic artifacts. Although presented for PPNB blade production herein, this method may be applied to other industries in different contexts or chronologies.

The accuracy of the analysis, on the basis of the error percentages for each predicted metric aspect, was high; however, some differences were observed among the three metrics measured in this study. The accuracy during the training had an error range of ~ 24/21% for both the proximal and distal measurements for the length, ~ 10/20% for the width, and ~ 30/25% for the thickness. These findings are very good results from an engineering viewpoint. Therefore, the most divergent element was the thickness and subsequently the length, and the least divergent element was the width error.

Despite the high predictive accuracy of the method applied to the production of the studied handmade flint artifacts, the error might appear higher than expected, because of the small number of artifacts sampled from each site. The artifacts used for both the validation and training processes was randomly selected among 70% of the studied artifacts, according to the neural network’s data processing system, thus decreasing the accuracy of the prediction. On the basis of this study, we therefore suggest using a larger number of artifacts to decrease the error. Nonetheless, some metric elements had relatively high standardization, such as the width, whereas other metric aspects, such as the length and thickness, show higher variability.

The results of the study showed that the width demonstrated the highest accuracy and a low error in predicting metrics. This suggests that precise control over width may be a key factor in standardized laminar production by knappers. This finding may be linked to the function and use preferences of laminar artifacts, such as the potential use of blades or blade fragments as inserted sickle blades (at Motza, Nahal Yarmuth 38, and Yiftahel) or for cutting and scraping without any modification, based on the visible wear on some of the artifacts (in all sites). The use of laminar blanks was often associated with intentional breakage to facilitate handling or insertion into specific supports, such as wooden structures. This highlights the importance of maintaining a standardized width. The findings indicate that users of blades required a consistent width to facilitate handling. In contrast, total length is often not preserved, as many formal tools that are not intentionally broken undergo significant retouching (e.g. arrowheads, perforators). Thickness, on the other hand, does not appear to play a significant role. It is important to note that the accuracy of measurements is influenced by the range of values for each metric. In this particular case, the three analyzed metrics of the artifact exhibit significant differences in their ranges. The length ranges from 15/20 mm to 80/105 mm, while the mesial width ranges from 9.5/12 mm to 28/33 mm. On the other hand, the medial thickness ranges from 1.3/2.5 mm to 11/15 mm. Considering these differences is crucial for a better understanding of the accuracy variations. Despite the narrow range of metrics, the width demonstrates a high level of accuracy. In contrast, the thickness exhibits lower accuracy, indicating less standardization in the production of laminar blanks as mentioned above, and is also affected by its narrow metrics range, contributing to the observed errors.

Moreover, the efficacy of our analysis allowed for a substantial decrease in errors by the observer during the analysis process of lithic samples, in our case dated to the MPPNB.

Our methodology, developed and implemented at MPPNB sites in the Southern Levant, may have relevance in other cultural contexts and time periods. The method’s applicability is underpinned by the consistent and standardized nature of the artifacts. As a result, we posit that this methodology can be widely applied to other contexts and sources of raw materials. When considering its application to lithic studies, it could also be utilized for analysing various types of tools. However, each tool category has its own set of parameters and metrics dictated by specific cultural preferences, which vary across different tools. Therefore, we suggest incorporating as many metric parameters as possible for each distinct tool type. It is important to note that the performance of neural networks in predicting metrics is heavily influenced by the irregularity of artifacts and the lack of consistent proportion or correlation (as a statistic measurement) in the metrics.

In summary, the analysis presented here reveals the intrinsic structures of the dataset studied, on the basis of a sequential reading that could not have been decoded by a human observer in the absence of data segmentation which implicitly involves information loss in the system as a whole. Moreover, for sites with a low availability or absence of complete laminar blanks, our method might provide a comparable data set for predicting/reconstructing artifacts that clearly belong to the same technological trajectory and indicate that the sites they come from share cultural affinities and chronology. At the same time, this methodology is an important element of technological subdivisions (e.g. blades/bladelets). Despite the extremely low alteration between the initial dataset and its predicted version, this study highlights the possibility to verify technological subdivisions, and potentially to suggest the presence of different cultural trajectories (e.g. bladelet-oriented vs blade-oriented productions).

Conclusion

Our application of a feedforward neural network analysis based on a hyperbolic tangent function as a tool to predict the original metrics of fragmented, reused, or damaged laminar artifacts showed positive results. The analysis was efficient, had high accuracy during the validation process, and had a relatively low statistical error. This study clearly demonstrated the standardization of the laminar blanks at the studied sites, highlighting a high level of control during knapping. The technological knowledge clearly spread beyond sub-regional boundaries, thus indicating that laminar blank production technology was part of a unified cultural koiné within the PPNB, specifically the MPPNB. The inter-variability analysis of the selected artifacts and the machine learning approach developed for metrics prediction, together promoted a better understanding of the laminar production involving standardized production from the middle-late stages of the reduction process. The findings may suggest connections among the studied regions and their similar needs regarding laminar blank production.

This analysis also demonstrated the potential of machine learning applications for archaeological data. Herein, the efficacy of the analysis indicated that a specific technological category, such as laminar blanks, can be metrically predicted, on the basis of the intrinsic standardization of Neolithic formal tools (such as sickle blades, arrowheads, etc.), particularly in the MPPNB. The results of this analysis were successful, due to the fact that the laminar blanks show regularity, since they originate in a clear technological trajectory used in PPNB sites.

In conclusion, the application of neural network analysis for the metric prediction of standardized laminar blanks from different sites of the Southern Levant shows technological homogeneity in the dimension preferences for laminar blanks, despite some technological and typological differences (such as the absence of sickle blades, or different typological details in arrowheads for example) across two diverse ecological regions.

This application not only demonstrates the ability to predict and reconstruct the original metrics of fragmented laminar blanks but also indicates the existence of a common cultural substratum, on the basis of highly controlled technology for laminar blank production.